Mechanical Engineering and Technology
Vol.
08
No.
06
(
2019
), Article ID:
33614
,
10
pages
10.12677/MET.2019.86054
Structural Topology Optimization Based on the Improved Hybrid Filter Method
Huabing Ouyang
School of Mechanical Engineering, Shanghai Dianji University, Shanghai

Received: Dec. 5th, 2019; accepted: Dec. 18th, 2019; published: Dec. 25th, 2019

ABSTRACT
In order to effectively solve the numerical instability problems of topology optimization, such as checkerboard and grayscale elements, a new structural topology optimization method based on improved hybrid filter method is proposed. Firstly, a density interpolation model based on bi-linear function is constructed. It eliminates the checkerboard phenomenon from the mathematical essence because of its continuity in the design domain; Secondly, a grayscale filtering strategy is imposed on the traditional optimization criterion, and an improved filtering technique combining sensitivity filtering and grayscale filtering is also proposed. Based on the method, the topology structure is updated and the gray unit can be effectively suppressed. Finally, the feasibility and effectiveness of the method are verified by three typical numerical examples.
Keywords:Variable Density Method, Interpolation Model, Structural Topology Optimization, Sensitivity Filter, Gray Scale Filter

基于混合式过滤策略的结构拓扑优化方法
欧阳华兵
上海电机学院机械学院,上海
收稿日期:2019年12月5日;录用日期:2019年12月18日;发布日期:2019年12月25日

摘 要
为了有效解决拓扑优化过程中所存在的棋盘格与灰度单元等数值不稳定问题,提出一种基于混合式过滤策略的结构拓扑优化方法。该方法首先构建了基于混合式拓扑优化密度插值模型,保证了其在设计域的连续性,从数学本质上可消除棋盘格现象;然后在传统优化准则中叠加灰度过滤策略,提出一种灵敏度过滤和灰度过滤相结合的改进过滤技术,从而实现结构的拓扑更新,该方法能有效抑制灰度单元;最后通过三个典型数值算例进一步验证了本文方法的可行性和有效性。
关键词 :变密度法,插值模型,结构拓扑优化,敏度过滤,灰度过滤

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 概述
近年来,拓扑优化逐步得到了广泛应用,拓扑优化旨在为给定设计域中找到材料的最佳布局,其求解过程是满足边界和荷载约束条件下目标对象最小化的迭代过程,通过利用目标函数与敏度约束,实现材料分布的逐步更新,其本质上是一种是否存在材料的离散变量优化组合问题 [1]。拓扑优化作为一种创成式设计方法,与尺寸优化和形状优化相比,赋予了更多的设计空间与设计自由度,提高了结构设计的合理性。
自1988年Bendsoe和Kikuchi提出均匀化的结构拓扑优化以来,连续体拓扑优化发展较快,特别是随着增材制造技术的发展,面向制造的拓扑优化技术及其工业应用也得到了广泛关注 [2]。目前,连续体拓扑优化的主要方法有:均匀化方法 [3] 、变密度法 [4] 、渐进结构优化法(ESO) [5] 、水平集方法 [6] 、优化准则法 [7] 、移动渐近线法和ICM方法 [8] 等。
目前,变密度法发展最为迅速,其基本思想是通过设计域的有限元离散化处理,将单元是否存在材质作为优化设计变量,构建给定材料相对密度与杨氏模量间的对应关系,最终将连续体的拓扑优化问题转化为0~1材料有无的组合优化问题。为了有效解决离散设计变量组合爆炸问题,经典变密度法中的固体各向同性惩罚材料(Solid Isotropic Material with Penalization, SIMP)通过引入幂函数材料插值方案,实现材料中间密度的惩罚处理,抑制中间密度单元的数量。然而,在SIMP插值过程中,惩罚因子的选取对拓扑优化结果影响甚大,其值不宜过大或过小。一方面,为了尽可能地抑制更多的中间密度单元(即灰度单元),应选择尽可能大的惩罚因子,使结果更逼近0或1的离散设计,但在求解过程中却容易将相对密度值较大的单元进行惩罚并被过早删除(特别是位于0.5~1间单元),进而影响后续的迭代搜索求解,容易出现棋盘格等数值不稳定现象,不便于得到最佳拓扑优化结果;另一方面,如果所选择的惩罚因子过小,惩罚效果就不明显,容易生成大量的中间密度单元,导致拓扑优化结果的边界模糊不清晰甚至难以识别,不利于后续设计与制造。
为了解决SIMP插值方法的不足,国内外科研人员开展大量的相关研究。Sigmund [9] 等引入了基于形态学限制方案作为密度过滤器,该方案能够有效消除固体和空体间的灰度。陈拥平 [4] 等针对散热结构的拓扑优化,提出了一种将灰度过滤和敏度过滤相结合的过滤机制,有效抑制了灰度单元的产生。龙凯 [10] 等一种考虑密度梯度的敏度过滤方法,消除了棋盘格现象和网络依赖性。杜义贤 [11] 等提出了一种具有逼近0/1极化优化准则法,有效抑制了灰度单元。Groenwold [7] 结合SIMP抑制灰度单元的方法,提出了一种启发式最优准则方法,得到了较为清晰的拓扑优化结构,但该方法迭代次数较多,效率不高。朱剑锋 [12] 等提出了一种敏度修正方法,达到了消除棋盘格、网格依赖性等目的。
除了材料插值模型外,拓扑优化过滤方法对灰度单元的影响也非常大,目前主要采用的方法有灰度过滤法 [13] 、敏度过滤法等措施 [10],但都无法有效消除灰度单元。为此,考虑到SIMP方法在材料插值模型及过滤方法的局限性,本文基于变密度法,构建了一种基于混合式材料插值模型,提出了基于传统优化准则(Optimality Criteria Method, OC)的敏度过滤与灰度过滤相结合的过滤方案,实现设计变量的更新和材料合理布局,该方案能够有效抑制灰度单元的产生。最后通过三个经典拓扑结构优化算例,采用本文所提方法并与文献 [14] 方法进行比较,进一步验证了本文所提方法在抑制灰度单元方面的有效性及其可行性。
2. 连续结构体拓扑优化设计
经典拓扑优化基本思路是以结构柔度最小化(即刚度最大小)为目标函数,以体积比为约束条件,找出满足给定载荷和边界条件下材料的最佳布局,其数学模型可表示为 [14] :
(1)
式(1)中:X为设计变量(本文为单元伪密度),其值在0~1范围内,为了防止计算时产生奇异矩阵, 一般可设置为0.001; 为结构的柔顺度(目标函数);U为结构总位移矩阵;K为结构总刚度矩阵;F为结构所受力向量; 为单元位移向量; 为归一化杨氏模量所对应的单元刚度矩阵;f为预设的体积比系数; 为优化后的材料体积; 为材料初始体积。
2.1. 经典SIMP材料插值模型
经典的变密度法的SIMP材料插值模型,将材料伪单元密度与杨氏模量间的关系由标准幂函数表示,其数学模型为:
(2)
上式中, 为伪单元密度; 为材料的弹性模量; 为惩罚后材料的弹性模量;p为惩罚因子,对中间密度单元的惩罚,使其尽量逼近于0或1,获得0/1的材料布局。
SIMP插值函数取不同惩罚因子时的函数曲线如图1所示。
由图1可知,随着惩罚因子的增大,曲线斜率不断越大,中间密度值趋向于0或1的效果越明显。然而,当惩罚因子过大时,中间大部分相对密度都趋近于0,导致大部分中间密度单元在迭代过程中被提早删除,其作用被弱化,不利于搜索到最有的拓扑结构。当惩罚因子过小时,则会导致过多的中间密度单元,则不利于最终结果的辨识。
2.2. 改进的材料插值模型
为了克服经典SIMP插值函数存在的问题,充分考虑引入新的材料插值模型,使相对密度位于0~0.5间时,杨氏模量趋近于0;相对密度值位于0.5~1.0间时,则使其趋向于1;而相对密度值为0.5时,则使其等概率地趋向0或1。这样就可以很好保证位于0.5~1间的大部分单元被误删,同时还可强化相对密度较大的单元,弱化相对密度较小的单元,最终保证拓扑结构寻优迭代过程的顺利进行,保证生成最优化的拓扑结构。
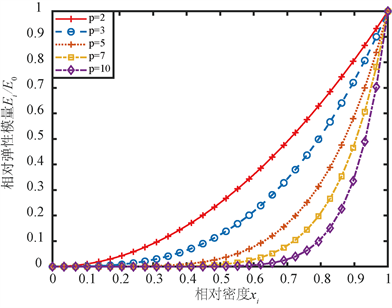
Figure 1. SIMP interpolation curve with different penalty factors
图1. 不同惩罚因子时SIMP插值曲线
基于上述思路,本文提出了一种改进的材料插值模型,其插值函数如式(3):
(3)
式(3)中,p为惩罚因子,其作用旨在通过改变曲线的斜率,控制中间密度单元快速趋近0或1;t为中间密度单元的惩罚,使其尽量逼近于0或1,获得0/1的材料布局。
图2所示为 时,p分别取不同只是改进后的插值函数的变化曲线。从图2可看出,当t保持恒定,随着惩罚因子p的增加,曲线斜率不断增大,这极大提高了中间密度的趋向0或1的速度。针对不同的工程应用问题,可通过设置合理的p和t值,以便得到更加符合设计要求的拓扑优化结果。

Figure 2. Improved interpolation function curve with different penalty factors
图2. 不同惩罚因子时改进的插值函数曲线
2.3. 灵敏度分析
通常,拓扑优化设计变量的数量都非常多,为了能准确快速地获的局部最小优化结果,需要求解每个变量的灵敏度。通过灵敏度分析,不仅可有效抑制拓扑优化过程中产生的棋盘格现象,而且还有利于加快拓扑优化的收敛速度,提高拓扑优化的求解效率。若以目标函数c为柔顺度,归一化后的单元伪密度为 ,则目标函数对单元伪密度的偏导数即为灵敏度,可由式(4)进行求解 [14] :
(4)
其中:c是柔顺度,K是整体刚度矩阵, 为第i个单元位移矢量, 是第i个单元的刚度矩阵。
2.4. 混合式过滤策略及设计变量优化
为了在拓扑优化过程中对大量的设计变量进行快速更新,目前广泛采用的方法主要有:优化准则法(Optimality Criteria, OC)、序列线性规划法(Sequential Linear Programming, SLP)和移动渐近线法(Method of Moving Asymptotes, MMA)。由于SIMP法中优化变量只有单元的相对密度,为了提高求解效率,本文采用改进OC法进行设计变量的更新 [7]。
虽然SIMP方法应用非常广泛,但如果处理不当,极易出现棋盘格现象和网格依赖性问题,目前通常采用灵敏度的过滤方法来进行处理,但在求解过程中,采用单纯的灵敏度过滤往往效果不太明显。因此,为了能有效抑制拓扑优化过程中间密度单元(即灰度单元)的产生,提高优化结构的轮廓可识别性及其可制造性,本文采用了一种将灵敏度过滤与灰度过滤相结合的混合式过滤机制,同时对传统的启发式更新策略进行了修正,引进了灰度抑制因子q,可有效抑制中间密度单元,其更新策略如式(5)所示 [14] :
(5)
式中: 为正向移动极限; 为阻尼因子,为了避免出现震荡现在保证稳定性与收敛些,本文选取0.5; 为单纯的灵敏度过滤;q为灰度抑制因子,控制中间灰度单元的产生; 可由最优化条件式(6)求解:
(6)
式中: 为拉格朗日乘子,可通过二分法求得。
由于叠加了灰度过滤策略,其原理与经典SIMP材料插值模型求解原理一致,通过构建拓扑优化变量间的非线性关系,对灵敏度过滤后位于0~1间的灰度单元继续进行惩罚,加快中间密度值趋向于0或1的速度,使得过滤效果更为明显。
具体的改进变密度拓扑优化求解流程图如图3所示。主要包括如下步骤:构建待求解问题的拓扑优化模型,并初始化设计变量;对结构设计域有限元分析,计算结构的应变能;计算目标函数,并对其求偏导,获取目标函数的灵敏度;采用灵敏度与灰度相结合的混合式过滤方法对设计变量更新迭代,抑制灰度单元生成;判断是否满足终止条件,若满足则停止,否则继续下一步迭代。

Figure 3. Flow chart for improved variable density topology optimization
图3. 改进的变密度拓扑优化求解流程图
3. 数值算例
为了验证所提改进拓扑优化方法在消除棋盘格与灰度单元方面的有效性和可行性,选取了三个经典数值算例,分别采用文献 [14] 和本文方法对其拓扑优化效果进行了比较分析。
3.1. 悬臂梁算例
如图4所示为60 cm × 30 cm的平面悬臂梁,左端固定,材料弹性模量 ,泊松比 ,右下角受垂直向下的集中载荷 (文中算例都为无量纲,下同),以柔顺度最小化为目标函数,采用4节点单元构建悬臂梁结构的拓扑模型。同时,选择体积比为0.5,考虑单元网格数为60 × 30,80 × 40与120 × 60的三种情况,过滤半径选取为宽度的0.04倍(下同),分别采用经典SIMP和本文所述方法进行优化求解,对其拓扑优化结果进行了比较,如图4为其拓扑优化结果,表1所示为其对应的优化结果。
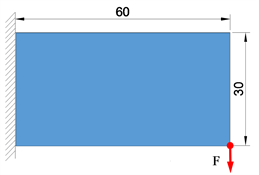
Figure 4. Simplified force model of cantilever beam
图4. 悬臂梁受力简化模型
从表1可知,采用经典SIMP方法,随着网格单元数增加,可在一定程度上降低棋盘格现象,但灰度单元无法得到有效控制;而采用本文所述的混合式改进策略方法,得到的拓扑结构轮廓更加清晰,基本能有效消除灰度单元并能有效抑制棋盘格现象,且随着网格数的增加,拓扑结构边界的光顺性得到有效提高,但仍然无法完全消除棋盘格现象。从表2中可知,随着网格数增加,系统柔顺度变化不大,进一步说明本文所述方法对网格没有依赖性,表2中灰度单元占比为将单元密度值位于[0.2,0.8]间的单元定义为灰度单元所得到的值(下同)。采用经典SIMP法灰度单元占比分别为29.67%,21.34%和14.21%;而采用本文所述方法,灰度单元完全消除,没有网格依赖性,同时迭代次数随网格数增加并没有明显增加。
Table 1. Topology optimization results of cantilever beam
表1. 悬臂梁拓扑优化结果
Table 2. Comparison of cantilever beam topology optimization
表2. 悬臂梁拓扑优化比较
3.2. MBB梁算例
如图5所示为180 × 30的平面MBB简支梁,两端固定,材料弹性模量 ,泊松比 ,根据其对称性,分析时只选取了一半结构,以柔顺度最小化为目标函数,构建MBB梁的拓扑结构优化模型。与算例1类似,仍然选择体积比为0.5,考虑单元网格数为60 × 20,90 × 30与150 × 50的三种情况,分别采用经典SIMP和本文所述方法对其拓扑优化结果比较分析,拓扑优化后结果如表3所示,对比分析优化结果如表4所示。
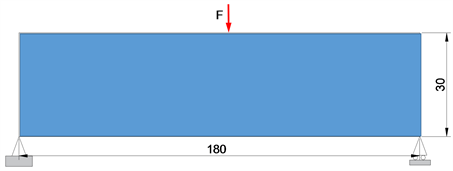
Figure 5. Simplified force model of MBB beam
图5. MBB梁受力简化模型
Table 3. Topology optimization results of MBB
表3. MBB梁拓扑优化结果
Table 4. Comparison of MBB topology optimization
表4. MBB梁拓扑优化比较
与算例1相类似,表3和表4分别为采用经典的SIMP方法与本文改进方法的拓扑对比结果,从结果可以看出,采用本文所提出的混合式方法能够有效抑制灰度单元的产生,灰度单元完全消失且没有网格依赖性,可获得非常清晰的拓扑轮廓。同时还可看出,本文方法较经典SIMP方法迭代次数明显减少;随着网格数的增加,迭代次数基本不变。
3.3. 热传导算例
为了进一步说明本文所述方法的有效性,以文献 [15] 中的热传导算例进行了对比分析。如图6所示为结构加载示意图,该结构为方形,边长为1 cm,厚度为0.01 cm,环境的初始温度为 ,左边中点散热器温度为 ,导热系数为0.001 W/(m3∙K),其余皆为绝热边界。

Figure 6. Schematic diagram of heat dissipation structure
图6. 散热结构示意图
分别采用经典SIMP和本文所述方法对其进行拓扑优化,其优化后的结果如表5所示,对比分析优化结果如表6所示。
Table 5. Topology optimization results of heat dissipation structure
表5. 散热器拓扑优化结果
Table 6. Comparison of heat dissipation structure topology optimization
表6. 散热器拓扑优化比较
类似于前两算例,分别采用经典SIMP方法与本文所提混合式方法对热传导进行比较分析,可得出与前两算例相一致的结论。本文方法能有效消除灰度单元,同时拓扑优化迭代次数明显减少,拓扑优化结构的边界更加清晰,过滤效果非常明显。
4. 结论
本文基于变密度法基本原理,以抑制灰度单元为目标,采用一种改进的SIMP插值函数,同时结合传统OC法基础上,提出了一种将敏度过滤与灰度过滤相结合的混合式过滤方法。并将传统的基于SIMP插值函数的OC法与本文所提出的混合式方法对拓扑优化结果进行了比较分析,通过三个经典算例结果表明,本文提出的方法可有效消除拓扑优化过程的棋盘格、灰度单元等数值不稳定性问题,不仅可以有效抑制了灰度单元的生成,而且获得了非常清晰的拓扑优化结果,进一步验证了本文方法的有效性和实用性。另外,本文研究方法可进一步推广到其他更加复杂的结构拓扑优化问题中。针对具体工程领域如增材制造等,探讨更加合理高效的拓扑优化求解策略将是未来拓扑优化发展方向及研究重点。
基金项目
上海市高峰高原学科(No. A1-5701-18-007-03);上海市教育委员会科研创新项目资助(14YZ158)。
文章引用
欧阳华兵. 基于混合式过滤策略的结构拓扑优化方法
Structural Topology Optimization Based on the Improved Hybrid Filter Method[J]. 机械工程与技术, 2019, 08(06): 466-475. https://doi.org/10.12677/MET.2019.86054
参考文献
- 1. Wang, F., Lazarov, B.S., Sigmund, O. and Søndergaard Jensen, J. (2014) Interpolation Scheme for Fictitious Domain Techniques and Topology Optimization of Finite Strain Elastic Problems. Computer Methods in Applied Mechanics and Engineering, 276, 453-472.https://doi.org/10.1016/j.cma.2014.03.021
- 2. Liu, J., et al. (2018) Current and Future Trends in Topology Optimization for Additive Manufacturing. Structural and Multidisciplinary Optimization, 57, 2457-2483. https://doi.org/10.1007/s00158-018-1994-3
- 3. Bendsøe, M.P. and Kikuchi, N. (1988) Generating Optimal Topologies in Structural Design Using a Homogenization Method. Computer Methods in Applied Mechanics and Engineering, 71, 197-224. https://doi.org/10.1016/0045-7825(88)90086-2
- 4. 陈拥平, 高亮, 肖蜜. 基于变密度法的散热结构拓扑优化设计[J]. 计算机集成制造系统, 2018, 24(1): 117-126.
- 5. Hardjasaputra, H. (2015) Evolutionary Structural Optimization as Tool in Finding Strut-and-Tie-Models for Designing Reinforced Concrete Deep Beam. Procedia Engineering, 125, 995-1000. https://doi.org/10.1016/j.proeng.2015.11.153
- 6. van Dijk, N.P., Maute, K., Langelaar, M. and van Keulen, F. (2013) Level-Set Methods for Structural Topology Optimization: A Review. Structural and Multidisciplinary Optimization, 48, 437-472. https://doi.org/10.1007/s00158-013-0912-y
- 7. Groenwold, A.A. and Etman, L.F.P. (2009) A Simple Heuristic for Gray-Scale Suppression in Optimality Criterion-Based Topology Optimization. Structural and Multidisciplinary Optimization, 39, 217-225. https://doi.org/10.1007/s00158-008-0337-1
- 8. Sigmund, O. and Maute, K. (2013) Topology Optimization Approaches: A Comparative Review. Structural and Multidisciplinary Optimization, 48, 1031-1055. https://doi.org/10.1007/s00158-013-0978-6
- 9. Sigmund, O. (2007) Morphology-Based Black and White Filters for Topology Optimization. Structural and Multidisciplinary Optimization, 33, 401-424. https://doi.org/10.1007/s00158-006-0087-x
- 10. 龙凯, 傅晓锦. 考虑密度梯度的敏度过滤方法[J]. 计算机辅助设计与图形学学报, 2014, 26(4): 669-674.
- 11. 杜义贤, 张严, 李涵钊. 具有逼近0/1离散特性的拓扑优化迭代算法[J]. 机械设计与研究, 2017, 33(1): 58-62.
- 12. 朱剑峰, 等. 连续体结构拓扑优化改进的敏度修正方法研究[J]. 中国机械工程, 2014(11): 1506-1510.
- 13. 昌俊康, 段宝岩. 连续体结构拓扑优化的一种改进变密度法及其应用[J]. 计算力学学报, 2009, 26(2): 188-192.
- 14. Sigmund, O. (2001) A 99 Line Topology Optimization Code Written in Matlab. Structural and Multidisciplinary Optimization, 21, 120-127. https://doi.org/10.1007/s001580050176
- 15. Philip Bendsoe, M. and Sigmund, O. (2003) Topology Optimization: Theory, Methods and Applications. Springer, Berlin.
