Modeling and Simulation
Vol.
10
No.
01
(
2021
), Article ID:
40236
,
10
pages
10.12677/MOS.2021.101005
基于文丘里混合的多孔介质燃烧火焰数值模拟研究
郑林1,廖晓炜2*,徐洪涛1,刘峰2
1上海理工大学能源与动力工程学院,上海
2中国特种设备检测研究院,北京

收稿日期:2020年9月29日;录用日期:2021年1月24日;发布日期:2021年2月3日

摘要
燃料/空气文丘里混合器在工业预混燃烧领域应用广泛,混合气体的均匀性对燃烧性能影响较大。为研究非均匀混合气体在多孔介质内的燃烧特点,本文对甲烷/空气经文丘里混合后预混不均匀度(spatial mixing deficiency, SMD)约为2%的非均匀预混气体在双层多孔介质燃烧器内的燃烧火焰进行了模拟。研究结果表明:受混合不均匀的影响,非完全预混气体在多孔介质内点火燃烧时容易产生局部高温而降低燃烧器的使用寿命;而达到稳定燃烧时,预混不均匀使得燃烧火焰稳定性降低。
关键词
非均匀预混,多孔介质,燃烧稳定性,数值模拟
Numerical Simulation Study of Incompletely Mixed Gas in Porous Media Combustion Flame Based on Venturi Mixture
Lin Zheng1, Xiaowei Liao2*, Hongtao Xu1, Feng Liu2
1School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai
2China Special Equipment Testing and Research Institute, Beijing

Received: Sep. 29th, 2020; accepted: Jan. 24th, 2021; published: Feb. 3rd, 2021

ABSTRACT
The fuel/air Venturi mixer is widely used in the industrial premixed combustion. The uniformity of the mixed gas has a great influence on the combustion performance. In order to study the combustion characteristics of non-uniform mixed gas in porous media, this paper studied the methane/air non-uniform premixed gas after Venturi mixing and the Spatial Mixing Deficiency (SMD) is about 2%, when entering in the double-layer porous media burner. The research results show that: due to the influence of uneven mixing, non-premixed gas easily leads to local high temperature when ignited and burned in the porous medium and reduces the service life of the burner. When stable combustion is achieved, due to the good thermal conductivity of porous medium, the local high temperature can be flattened, but flame stability becomes worse.
Keywords:Incomplete Premixing, Porous Media, Combustion Temperature, Numerical Simulation

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
与传统的燃烧技术相比,多孔介质燃烧技术具有结构简单紧凑、功率调节范围大、燃烧稳定性好、燃烧效率高和污染物排放低等优点 [1]。
学者们针对多孔介质燃烧特性已开展了大量的研究。Filho和Pimenta [2] 通过数值模拟的方法分别模拟双层多孔介质中上游预热区和下游燃烧区多孔介质材料物性对燃烧过程中CO排放的影响,发现上游多孔介质物性影响较小而下游多孔介质影响较大。Shi等 [3] 通过实验和数值模拟的方法研究了CH4预混气体在由3 mm氧化铝小球填充多孔介质燃烧器中的贫燃特性。研究发现当量比对燃烧火焰前端的倾斜和破碎有重要影响。Hashemi和Hashemi [4] 模拟研究了不同当量比条件下CH4预混气体浸没燃烧的稳燃范围,发现当量比较低时燃烧稳定性变差。Liu等 [5] 模拟研究了入口速度、当量比、多孔介质消光系数、导热系数等因素对CH4预混气体分别在以氧化锆和氧化铝填充的双层多孔介质中的燃烧特性的影响。Bubnovich等 [6] 模拟了氧化铝小球填充的单层和双层多孔介质燃烧器的燃烧特性,并考虑了Zeldovich路线中高温对NOx的形成机理,发现双层多孔介质燃烧器NOx排放更低。Nemoda等 [7] 利用数值模拟的方法研究比较了双层多孔介质浸没燃烧和单层多孔介质表面燃烧的燃烧特性,揭示了双层多孔介质燃烧时预热区固体可预热气体,燃烧区气体加热固体以降低燃烧温度的独特燃烧特性。Brenner等 [8] 基于局部热平衡假设对二维燃烧模型进行了模拟,并考虑了详细化学反应机理,对燃烧器中CO、OH等组分在燃烧器中的分布进行了预测。Barra等 [9] 对双层多孔介质燃烧的稳定性进行数值模拟发现:上层多孔介质应具有更低的导热系数和孔隙率以防止回火,而下游则应该增大导热系数以使得更多的热量流向上游。郑成航等 [10] 模拟研究了CH4气体在单层氧化铝小球填充的燃烧器中浸没燃烧的火焰特性,并分析了不同入口速度下的火焰形状,发现在速度比较低时火焰轮廓比较平整,而随着入口速度的增大火焰轮廓呈抛物线形状。
总之,多孔介质作为目前燃烧技术中的热点,很多学者都对多孔介质燃烧技术进行了研究。但从已发表的文献中看,由于多孔介质燃烧具有良好的稳定性,人们在模拟研究多孔介质的燃烧时,基本上都认为甲烷和空气均匀预混之后在多孔介质燃烧器内燃烧,而很少考虑燃料的混合不均匀度对其燃烧的影响。而在实际工业预混燃烧领域中,预混气体的均匀性对燃烧过程影响较大。如邵卫卫等 [11] 发现随着气体预混不均匀度的增加燃烧NOx排放增加。因此,为了提高燃料与空气的混合效果,李宇红 [12] 等通过优化圆柱形射流预混段的几何结构来提高预混段的混合能力。谢刚等 [13] 通过减少孔的数目、改变孔的直径及喷孔位置来提高DLN燃烧室的混合均匀度等。
文丘里混合器因其结构简单、紧凑而在工业预混领域应用广泛。而多孔介质燃烧技术作为一种新型燃烧技术,在预混燃烧领域具有广泛的应用前景。因此研究文丘里–多孔介质燃烧相结合的非均匀预混气体在多孔介质燃烧器中的燃烧规律,在工业应用上具有十分重要的研究意义。
2. 数值模拟
2.1. 物理模型
图1表示文丘里混合器和多孔介质燃烧器相结合的文丘里–多孔介质燃烧器二维几何模型。甲烷和空气先经文丘里混合器混合之后,再进入双层多孔介质燃烧器中进行燃烧。整个模型长度为270 mm,直径为40 mm,喉部直径为10 mm。空气由左侧入口进入,甲烷从喉部进入,喉部长度为2 mm。利用文丘里效应使甲烷和空气经文丘里混合之后再进入双层多孔介质燃烧器内进行燃烧。
双层多孔介质燃烧器,预热区长30 mm,由直径为5 mm的氧化铝小球填充,孔隙率为0.4,主要是用来预热来流气体和防止燃烧火焰发生回火;燃烧区长50 mm,使用孔隙率为0.77的碳化硅泡沫陶瓷进行填充。氧化铝和碳化硅热物性参数如表1所示 [4]。
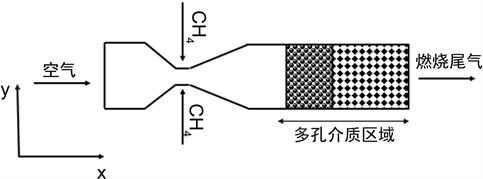
Figure 1. Schematic diagram of porous burner
图1. 文丘里混合器几何模型
Table 1. Thermo-physical properties of Al2O3 and SiC
表1. 氧化铝和碳化硅热物性参数
2.2. 计算方法
由于多孔介质内的燃烧反应涉及剧烈的气–气、气–固体之间的导热、对流、辐射等不同换热方式的紧密耦合,因此,为了简化燃烧反应模型本文做了如下假设:
1) 假设气体为不可压缩流体;
2) 多孔介质骨架为灰体且各向同性;
3) 多孔介质对燃烧反应没有催化作用并忽略由于多孔介质对气体的阻挡而产生的扰动对甲烷和空气产生的混和,既忽略弥散效应;
4) 忽略重力对气体的作用;
5) 参与燃烧反应的各组分以及燃烧产物为不可压缩理想气体。
6) 气体混合物在燃烧过程中各组分的化学性质(活化能Ea,指前因子等)不变。
燃烧模拟分析中的数学控制方程描述如下:
1) 连续性方程
(1)
式中, 表示气体密度, 表示气体速度, 表示多孔介质孔隙率,在非多孔介质区域孔隙率为1。
2) 动量守恒方程
(2)
式中, 表示流体的动力粘度, 表示外界向流体施加的力,即体积力,在本文中根据假设,有 ; 表示由多孔介质在流体流动时所施加的阻力。根据由达西定律拓展的Forchheimer方程其阻力损失表示为 [5]:
(3)
式中,第一项表示由于流体的粘性和多孔介质之间的相互作用而产生的粘性阻力, 表示粘性阻力系数;第二项中 表示为惯性阻力系数。对于本文中使用的由小球填充成的多孔介质模型,上式可改为实验修正后的尔格方程 [14]:
(4)
式中, 表示颗粒直径。A、B的值需实验测定。Macdonald等人在1979年曾提出经验常数为A = 180,B = 1.8,而在非多孔介质区域则没有该项。
(1) 组分输运方程
(5)
式中, 表示第i种组分的质量分数, 表示第i组分的扩散速度, 表示组分i的绝对速度, 表示第i种组分的反应速率, 表示第i种组分的摩尔质量。
3) 能量方程
(6)
式中, 指组分i的焓值, 指组分i的摩尔质量, 指有效导热系数,包括气相和固相两部分的导热。
4) 理想气体状态方程
(7)
式中,n指气体摩尔数,R指通用气体常数,其值为8.314 J/(mol·K)。
2.3. 数值方法
选择标准k-ε模型来模拟空气和甲烷的混合,采用离散坐标法(Discrete Ordinates)辐射模型来处理多孔介质的内部辐射 [10];由于本文只关心燃烧过程中所表现出的热效应,因此选取CH4/air一步反应机理来描述CH4的燃烧反应 [4] [5],反应的指前因子为2.119e11,活化能为2.027e8 J/mol。
采用高质量的结构化网格对整个计算区域进行网格划分;采用控制容积法来离散各守恒方程并使用SIMPLE算法来求解基于压力–速度耦合的二阶迎风差分格式的动量方程。同时将能量方程松弛因子设置为0.8以防止迭代发散。
2.4. 参数计算
假设空气只含氧气和氮气。根据甲烷与空气的一步燃烧反应方程式:
(8)
式中,L指过量空气系数。由此可得完全预混气体中甲烷的摩尔分数为:
(9)
通过甲烷的摩尔分数可计算出文丘里混合器中甲烷入口处的速度:
(10)
式中,v指完全预混状态下甲烷和空气完全预混气体的入口速度。 指文丘里混合器中甲烷入口处的截面积,v指完全预混气体入口处截面面积。
同理可得出文丘里混合器中空气入口处的速度:
(11)
为了保证混合不均匀的甲烷气体在多孔介质燃烧器内能充分燃烧,选取 、 并根据上式计算出的 、 行数值模拟。
同时,采用预混不均匀度S来评估空气/甲烷的混合效果。预混不均匀度S的表达式如下 [11]:
(12)
式中, 指截面上的平均摩尔分数,本文中指过量空气系数为1.4时甲烷的平均摩尔分数, 。
2.5. 边界条件
入口处:
对于气相: ,,
出口处:
对于气相:
由于出口处温度较高,需考虑出口处多孔介质的对外辐射:
壁面使用绝热以及无滑移边界条件。而且为了保证燃烧反应的顺利进行,先将甲烷/空气混合气体通入燃烧器内一段时间,待初场稳定后,再在燃烧区点火。
3. 计算结果及分析
3.1. 文丘里混合性能分析
图2、图3表示在冷态条件下模拟得出的甲烷质量分数分布云图和在多孔介质燃烧器入口处横向(y方向)位置上的甲烷浓度分布。由图可以看出甲烷和空气经文丘里混合器混合之后进入多孔介质燃烧器的是存在一定混合不均匀度的非完全混合气体。并且根据式(12)计算出此时预混气体进入燃烧器的混合不均匀度SMD约为2%。
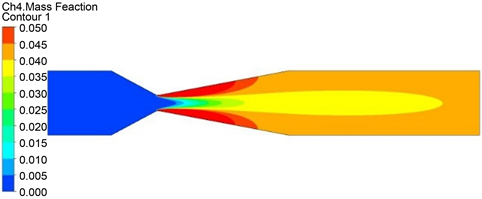
Figure 2. Contour of methane mass fraction
图2. 甲烷质量分数分布云图
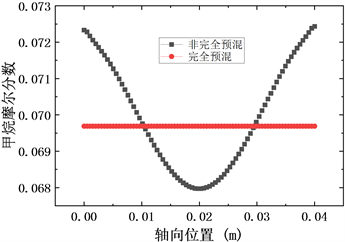
Figure 3. Horizontal position distribution of methane mole fraction
图3. 甲烷摩尔分数横向位置分布
3.2. 非均匀预混多孔介质燃烧
图4表示完全预混和非完全预混两种模型在双层多孔介质燃烧器内点火之后,不同时刻所对应的轴线温度分布。由图4(a)可以看出:两种模型在多孔介质燃烧器内燃烧到3.6秒时,由于甲烷还未完全燃烧以及烟气还未及时将热量传递至下游使得高温区域较窄。同时,随着燃烧的进行,甲烷进一步完全反应以及烟气不断和下游多孔介质进行换热,使得上游高温区域不断变宽,下游的温度也随之升高,即如图4(b)、图4(c)所示。
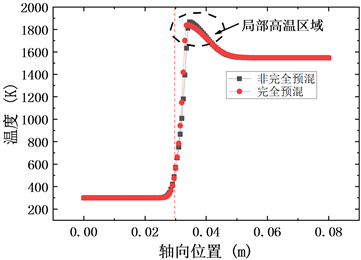 (a) 3.6秒时两种模型轴向温度分布
(a) 3.6秒时两种模型轴向温度分布
 (b) 7.2秒时两种模型轴向温度分布
(b) 7.2秒时两种模型轴向温度分布
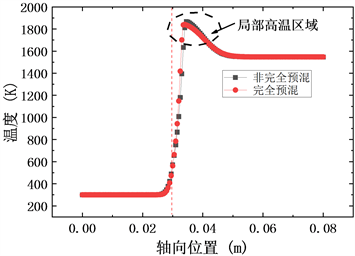 (c) 18秒时两种模型轴向温度分布
(c) 18秒时两种模型轴向温度分布
Figure 4. Axial temperature distribution of the two models at different seconds
图4. 不同时刻两种模型轴向温度分布
此外,由图4(a)~(c)也可以看出:受到甲烷和空气混合不均匀度的影响,和完全预混气体在多孔介质内的燃烧相比,非完全预混气体在多孔介质内燃烧时更容易产生局部高温(图中虚线线框区域)。因此,为研究在点火过程中局部高温的持续时间,图5表示两种模型从点火开始燃烧至60秒的过程中,多孔介质燃烧器中燃烧最高温度随时间的变化规律。
由图5可以看出在燃烧开始的60秒内非完全预混气体在多孔介质内的燃烧最高温度均比完全预混气体的燃烧最高温度高。这说明受到混合不均匀度的影响,和完全预混燃烧相比,非完全预混燃烧在从点火开始的较长一段时间内都容易产生局部高温,这对于多孔介质燃烧器而言是非常不利的,较长时间的局部高温容易烧坏多孔介质而降低燃烧器的使用寿命。此外,正如文献 [11] 中的结论:预混不均匀容易产生高温炙热点而使NOx的排放增大。
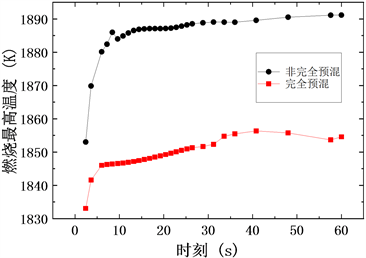
Figure 5. Maximum combustion temperature at different times
图5. 不同时刻下最高燃烧温度的变化
图6表示两种模型分别燃烧到172秒和272秒时的轴向温度变化。由图可知无论是预混燃烧还是非完全预混燃烧在172秒和272秒时的轴向温度分布都已基本重合,这说明在172秒以后燃烧已基本趋于稳定。
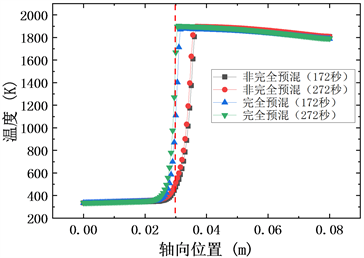
Figure 6. Axial temperature distribution
图6. 轴向温度分布
图7表示燃烧至272秒达到稳定燃烧时,两种模型的燃烧温度分布云图。由图7(a)可以看出由于双层多孔介质燃烧器具有良好的燃烧稳定性,完全预混燃烧的火焰面前端可以非常平整的稳定在交界面(x = 0.03 m)处开始燃烧。
而由图7(b)并结合图3、图6可以看出:由于受到混合不均匀度的影响,使得非均匀预混燃烧的火焰面明显发生了倾斜和弯曲。这说明和完全预混燃烧相比,燃料的混合不均匀度使得非完全预混燃烧的火焰稳定性变差。
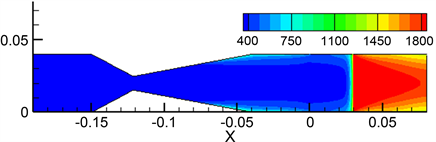 (a) 完全预混燃烧
(a) 完全预混燃烧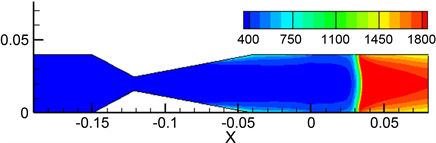 (b) 非完全预混燃烧
(b) 非完全预混燃烧
Figure 7. Temperature contour of two combustion models (K)
图7. 两种燃烧模型温度分布云图(单位K)
4. 结论
本文结合工业预混领域常用的文丘里混合器及双层多孔介质燃烧技术,数值模拟研究了经文丘里混合器混合之后的混合不均匀度SMD约为2%的非完全预混气体在双层多孔介质燃烧器内的燃烧火焰特点。本文主要得出了以下结论:
1) 受到甲烷混合不均匀性的影响,非完全预混气体在多孔介质燃烧器中从点火开始到稳定燃烧的过程中容易产生局部高温而降低燃烧器的使用寿命。
2) 在达到稳定燃烧时,完全预混气体可以在多孔介质燃烧器内稳定燃烧,而预混不均匀使得非完全预混气体在多孔介质内的燃烧稳定性变差,其燃烧火焰发生了明显倾斜和弯曲。
因此,基于以上结论,尽管双层多孔介质燃烧具有较好的稳定性,但与完全预混气体燃烧相比预混不均匀仍会导致局部温度过高和燃烧稳定性变差等不良后果。这对今后多孔介质燃烧器性能的优化研究来说具有重要的参考价值。
基金项目
国家重点研发计划(2017YFF0209806)。
文章引用
郑 林,廖晓炜,徐洪涛,刘 峰. 基于文丘里混合的多孔介质燃烧火焰数值模拟研究
Numerical Simulation Study of Incompletely Mixed Gas in Porous Media Combustion Flame Based on Venturi Mixture[J]. 建模与仿真, 2021, 10(01): 38-47. https://doi.org/10.12677/MOS.2021.101005
参考文献
- 1. 程乐鸣, 岑可法, 周昊, 等. 多孔介质燃烧理论与技术[M]. 北京: 化学工业出版社, 2012.
- 2. Filho, R.C.M. and Pimenta, A.P. (2011) A Two-Dimensional Numerical Simulation of Combustion and Heat Transfer in Radiant Porous Burners. Combustion Science & Technology, 183, 370-389. https://doi.org/10.1080/00102202.2010.520278
- 3. Shi, J.R., Yu, C.M., Li, B.W., et al. (2013) Experimental and Numerical Studies on the Flame Instabilities in Porous Media. Fuel, 106, 674-681. https://doi.org/10.1016/j.fuel.2013.01.010
- 4. Hashemi, S.M. and Hashemi, S.A. (2017) Flame Stability Analysis of the Premixed Methane-Air Combustion in a Two-Layer Porous Media Burner by Numerical Simulation. Fuel, 202, 56-65. https://doi.org/10.1016/j.fuel.2017.04.008
- 5. Liu, H., Dong, S., Li, B.W., et al. (2010) Parametric Investigations of Premixed Methane-Air Combustion in Two-Section Porous Media by Numerical Simulation. Fuel, 89, 1736-1742. https://doi.org/10.1016/j.fuel.2009.06.001
- 6. Bubnovich, V., Henríquez, L. and Gnesdilov, N. (2007) Numerical Study of the Effect of the Diameter of Alumina Balls on Flame Stabilization in a Porous-Medium Burner. Numerical Heat Transfer, 52, 21. https://doi.org/10.1080/00397910601149942
- 7. Nemoda, S., Trimis, D. and Živković, G. (2004) Numerical Sim-ulation of Porous Burners and Hole Plate Surface Burners. Thermal Science, 8, 3-17. https://doi.org/10.2298/TSCI0401003N
- 8. Brenner, G., Pickenäcker, K, Pickenäcker, O., et al. (2000) Numerical and Experimental Investigation of Matrix-Stabilized Methane/Air Combustion in Porous Inert Media. Combustion and Flame, 123, 201-213. https://doi.org/10.1016/S0010-2180(00)00163-2
- 9. Barra, A.J., Diepvens, G., Ellzey, J.L., et al. (2003) Nu-merical Study of the Effects of Material Properties on Flame Stabilization in a Porous Burner. Combustion and Flame, 134, 369-379. https://doi.org/10.1016/S0010-2180(03)00125-1
- 10. 郑成航, 程乐鸣, 李涛, 等. 多孔介质燃烧火焰面特性数值模拟[J]. 中国电机工程学报, 2009, 29(5): 48-53.
- 11. 邵卫卫, 赵岩, 刘艳, 等. 燃气轮机燃烧室预混燃烧器天然气燃料/空气掺混均匀性研究[J]. 中国电机工程学报, 2017(3): 148-156.
- 12. 李宇红, 孙宝成, 祁海鹰. 燃烧室预混段燃料/空气混合规律的数值研究[J]. 热能动力工程, 2008, 23(3): 235-239.
- 13. 谢刚, 李宇红, 祁海鹰. DLN燃烧室的燃料-空气预混均匀性研究[J]. 工程热物理学报, 2006, 27(z2): 227-230.
- 14. 邓彩华, 童亮, 陈壁峰, 等. 多孔介质流动的直接数值模拟[J]. 武汉理工大学学报: 交通科学与工程版, 2011, 35(6): 1257-1260.
NOTES
*通讯作者。
