Statistical and Application
Vol.3 No.02(2014), Article
ID:13658,7
pages
DOI:10.12677/SA.2014.32010
Statistical Analysis for Nonlinear Joint Mean and Variance Models
Department of Statistics, Zhejiang Agriculture and Forest University, Hangzhou
Email: 175384319@qq.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Apr. 25th, 2014; revised: May 23rd, 2014; accepted: Jun. 3rd, 2014
ABSTRACT
We propose nonlinear joint mean and variance models in this paper and investigate the estimate for unknown parameters in the model based on Gauss-Newton iterative algorithm. Furthermore, we make some simulations to show that the proposed procedure works satisfactorily. Lastly, two real examples are presented to illustrate the proposed methodology.
Keywords:Nonlinear Joint Mean and Variance Models, Heteroscedasticity, Gauss-Newton, Maximum Likelihood Estimate

非线性联合均值方差模型的统计分析
周梦齐,徐登可,杨佳红,王梦滢
浙江农林大学统计系,杭州
Email: 175384319@qq.com
收稿日期:2014年4月25日;修回日期:2014年5月23日;录用日期:2014年6月3日

摘 要
在提出非线性均值方差模型的基础上,研究了该模型中未知参数的估计问题。主要是基于Gauss-Newton迭代算法给出该模型中未知参数的极大似然估计。通过大量随机模拟实验验证了所提出方法的有效性。最后,结合实际问题数据验证了该模型与方法具有实用性和可行性。
关键词
非线性联合均值方差模型,异方差,Gauss-Newton,极大似然估计

1. 引言
在回归模型中,对误差项进行等方差假设是一个标准的假设。违反这个假设,估计量的有效性就可能得不到保证。因此很重要也很有必要去处理回归分析中的异方差情况。很多作者已经讨论了异方差情况下不同模型的估计和检验等统计推断问题。White[1] 提出了在异方差线性回归模型下参数协方差阵的估计,这种估计不依赖于异方差的结构形式模型;Andrews[2] 介绍了异方差和自相关函数形式未知的情形下协方差阵的估计;Smyth[3] 基于异方差回归模型研究了模型中未知参数的限制极大似然估计。
事实上,随着人们对现实世界越来越深入的认识,很多现实生活的事件、现象、过程等也表现得越来越复杂,这也将导致我们研究的实际数据也是错综复杂的。如果只是用简单的统计模型来描述和研究,很多分析已经不能得到真实的接近实际的结果。因此我们很有必要针对这些复杂现象,采用比较复杂的模型来描述,联合均值方差模型就是其中一种。有关基于均值方差同时建模的双重回归异方差模型也已有了大量的研究成果。Park[4] 在高斯模型中提出了方差参数的对数线性模型,采用两阶段过程来估计参数;Harvey[5] 在一般条件下讨论了均值和方差效应的极大似然估计和子序列似然比检验;Aitkin[6] 提供了联合均值和方差模型的极大似然估计,并且把它应用到了Minitab tree数据中;Verbyla[7] 利用限制极大似然估计参数和在MLE和限制似然下考虑了模型的影响诊断分析;Wu和Li[8] 提出了逆高斯分布的均值和方差联合建模模型的同时变量选择问题;Xu等[9] 基于惩罚伪似然研究了双重广义线性模型的变量选择问题;吴刘仓等[10] 基于Box-Cox变换下研究了联合均值与方差模型的参数估计;马婷等[11] 基于偏正态分布联合位置、尺度与偏度模型给出了该模型参数的估计方法;徐登可等[12] 基于双重logistic回归模型对影响妊高病的危险因素进行变量选择和预测分析。
总之,有关异方差数据处理方法以及用均值方差模型处理异方差数据都已经有了很多的研究成果。虽然,对于均值方差同时建模双重回归异方差模型已经有了大量的研究成果,但是上述成果大多数都是基于线性模型,很少有推广到非线性模型。而在现实生活数据中的变量与变量之间的关系可能存在非线性关系,因此我们很有必要基于非线性模型发展一种非线性联合均值方差模型。
故本文主要目的是基于Gauss-Newton迭代算法研究提出的非线性联合均值方差模型的极大似然估计以及考虑其应用。我们的方法在非线性的基础上能同时对均值和方差建立模型,使得均值方差模型更加一般化,也更具有应用的广泛性。最后,通过随机模拟和实例研究分析表明所提出的模型与方法是有用和有效的。
本文的组织结构安排如下:第2节,首先介绍了非线性均值方差模型;然后给出了模型中未知参数的极大似然估计。第3节,详细介绍了Gauss-Newton迭代算法。第4节,通过随机模拟实验验证该方法的有效性。第5节,结合实际问题数据验证该模型与方法的实用性与可行性。最后是本文的小结与讨论。
2. 非线性联合均值方差模型
首先针对异方差数据和基于非线性回归,我们既对均值建模,同时又对方差进行建模,提出如下非线性联合均值方差模型:
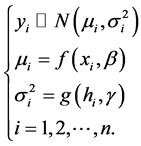 (1)
(1)
其中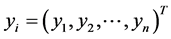 为响应变量,
为响应变量,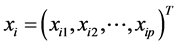 和
和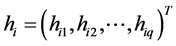 分别为影响均值部分和方差部分的解释变量,
分别为影响均值部分和方差部分的解释变量, 是非线性均值模型中的未知参数,
是非线性均值模型中的未知参数,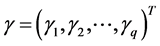 是非线性方差模型中的未知参数。
是非线性方差模型中的未知参数。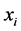 、
、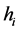 两个解释变量可能完全不相同,完全相同或者部分相同,即均值模型、方差模型可能包含不同的解释变量,包含相同的解释变量也可能包含部分相同的解释变量。
两个解释变量可能完全不相同,完全相同或者部分相同,即均值模型、方差模型可能包含不同的解释变量,包含相同的解释变量也可能包含部分相同的解释变量。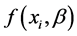 是一个含有未知参数
是一个含有未知参数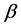 的已知非线性函数,
的已知非线性函数,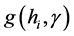 是一个含有未知参数
是一个含有未知参数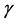 的已知非线性函数。若
的已知非线性函数。若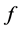 和
和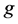 变成了线性函数,那么
变成了线性函数,那么 ,
,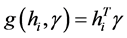 ,即变成了线性均值方差模型,也就是说线性均值方差模型是该模型的一种特例。
,即变成了线性均值方差模型,也就是说线性均值方差模型是该模型的一种特例。
由模型(1)可以得到:
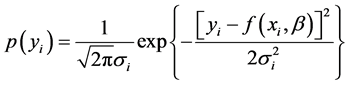 (2)
(2)
对(2)式两边取自然对数,得到:
 (3)
(3)
由(3)式可得到对数似然函数:
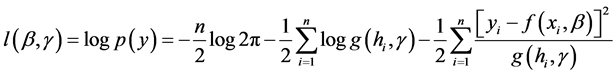 (4)
(4)
3. 参数的极大似然估计
3.1. Gauss-Newton迭代算法
由于该模型无法通过普通的极大似然估计得到参数估计的显示表达式,所以我们采用了GaussNewton迭代算法。
为了方便,令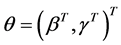 ,则
,则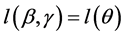 ,因此
,因此
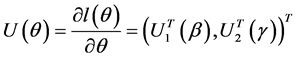 (5)
(5)
其中
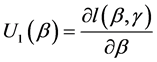 ,
,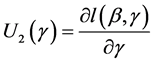 , (6)
, (6)
 (7)
(7)
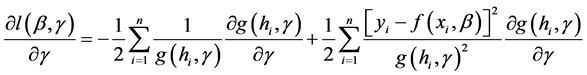 (8)
(8)
另外,令
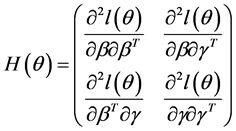 ,其中 (9)
,其中 (9)
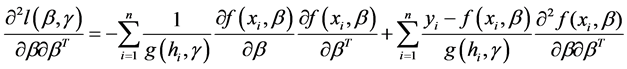 (10)
(10)
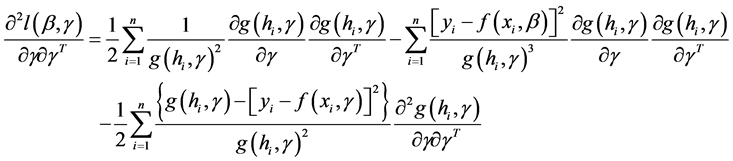 (11)
(11)
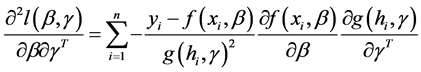 (12)
(12)
 (13)
(13)
最后,将(5)-(13)这9个式子带入下面的(14)式进行迭代计算,
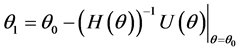 (14)
(14)
直到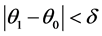 ,即认为
,即认为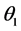 为
为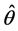 的极大似然估计的近似值,其中
的极大似然估计的近似值,其中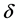 为预先给定的充分正小数,如
为预先给定的充分正小数,如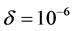 。
。
3.2. 迭代步骤
给出以下算法步骤对模型(1)中的参数进行极大似然估计迭代计算。
步骤1:给定参数的迭代初值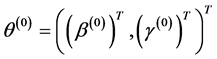 ;
;
步骤2:给定当前值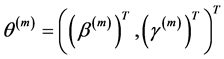 ,代入下式进行迭代更新
,代入下式进行迭代更新
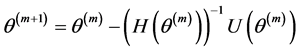 ;
;
步骤3:重复步骤2,直到迭代收敛。
4. 模拟
接下来我们对上述参数估计方法的有限样本性质进行模拟研究,参数的估计精度使用均方误差(MSE)来评价和衡量,其定义如下:
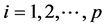
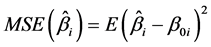 ,
,
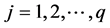
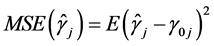 .
.
其中,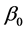 和
和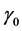 分别是
分别是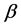 和
和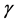 的真值,
的真值,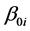 和
和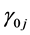 分别是
分别是 和
和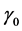 的第
的第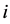 个分量和第
个分量和第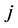 个分量。我们将通过下面两个具体的非线性联合均值方差模型例子来说明所提出模型与方法的有效性。
个分量。我们将通过下面两个具体的非线性联合均值方差模型例子来说明所提出模型与方法的有效性。
4.1. 例子1
根据模型(1),建立如下的具体的非线性联合均值方差模型(15),根据该模型并产生模拟数据
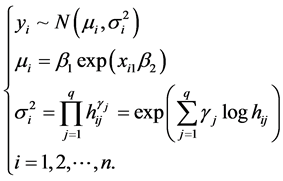 (15)
(15)
其中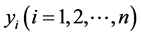 相互独立,且服从正态分布
相互独立,且服从正态分布 ,
, 和
和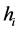 的分量分别相互独立,且
的分量分别相互独立,且 产生于均匀分布
产生于均匀分布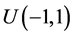 ,
,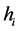 产生于均匀分布
产生于均匀分布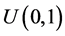 。
。 的真值取
的真值取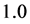 ,
,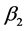 的真值取
的真值取 ,
,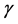 的真值为
的真值为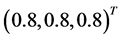 ,取样本量
,取样本量 ,重复模拟
,重复模拟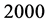 次。具体模拟结果见表1。
次。具体模拟结果见表1。
表1结果显示,模型(15)中的参数的估计随着样本量的递增越来越接近真实值,参数极大似然估计的均方误差也越来越小,这说明模型(15)所使用的极大似然估计方法取得了较理想的效果。
4.2. 例子2
根据模型(1),建立如下的具体的非线性均值方差模型(16),根据该模型并产生模拟数据
 (16)
(16)
其中 相互独立,且服从正态分布
相互独立,且服从正态分布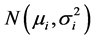 ,
,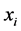 和
和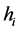 的分量分别相互独立,且
的分量分别相互独立,且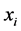 产生于均匀分布
产生于均匀分布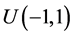 ,
,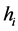 产生于均匀分布
产生于均匀分布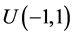 。
。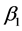 的真值取
的真值取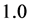 ,
,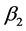 的真值取
的真值取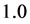 ,
,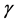 的真值取
的真值取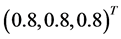 ,取样本量
,取样本量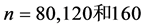 ,重复模拟
,重复模拟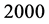 次。具体模拟结果见表2。
次。具体模拟结果见表2。
Table 1. Maximum likelihood estimate of unknown parameters in nonlinear joint mean and variance models in Example 1
表1. 例1中非线性联合均值方差模型中未知参数的极大似然估计结果
Table 2. Maximum likelihood estimate of unknown parameters in nonlinear joint mean and variance models in Example 2
表2. 例2中非线性联合均值方差模型中未知参数的极大似然估计结果
表2结果显示,模型(16)中的参数的估计随样本量的递增越来越接近真实值,参数极大似然估计的均方误差也越来越小,这说明模型(16)所使用的极大似然估计方法取得了较理想的效果。
5. 实例分析
5.1. 伦福德冷却实验数据
1978年,Count Rumford得到一组摩擦生热的数据[13] 。首先在一个固定的炮管内插入一只钝管,应用螺丝固定在炮管的底部。让一对马连续转动达30分钟,然后再设置一只温度计。在将近45分钟内,每隔一段时间观察温度的变化,并记录温度的大小。
利用SPSS软件对伦福德数据进行正态性检验,得到图1为伦福德数据正态检验的P-P图,我们可以从图中发现,伦福德数据基本服从或近似服从正态分布。
因此利用模型(15),建立如下模型:
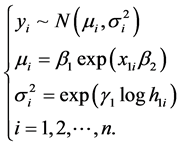 (17)
(17)
其中,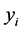 为不同时间炮管的温度,
为不同时间炮管的温度,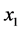 为时间(在该模型中令
为时间(在该模型中令 与
与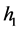 相同),通过计算可得:
相同),通过计算可得: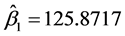 ,
,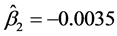 ,
,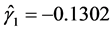 。这也表明该数据中变量间存在一定的非线性关系。
。这也表明该数据中变量间存在一定的非线性关系。
5.2. 氟哌啶醇血浆浓度数据
1975年,Wagner记录了氟哌啶醇血浆浓度的数据[13] 。
利用SPSS软件对氟哌啶醇血浆浓度数据进行正态性检验,得到图2为氟哌啶醇血浆浓度数据正态检验的P-P图,我们可以从图中发现,氟哌啶醇血浆浓度数据基本服从或近似服从正态分布。
因此利用模型(16),建立如下模型:
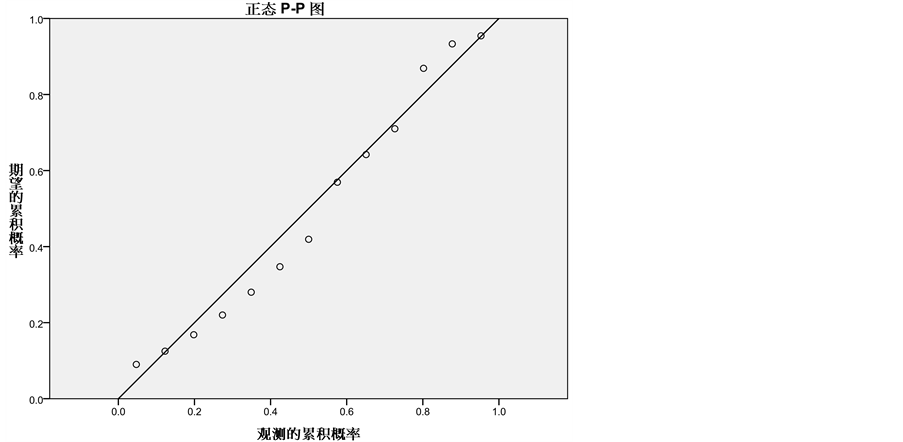
Figure 1. Normal P-P plot for Rumford data
图1. 伦福德数据的正态P-P图

Figure 2. Normal P-P plot for concentration data of haloperidol plasma
图2. 氟哌啶醇血浆浓度数据的正态P-P图
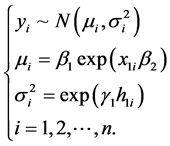 (18)
(18)
其中,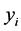 为氟哌啶醇血浆浓度,
为氟哌啶醇血浆浓度,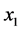 为时间(在该模型中令
为时间(在该模型中令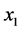 与
与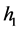 相同),通过计算可得:
相同),通过计算可得: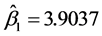 ,
,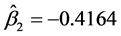 ,
,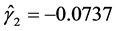 。这也表明该数据中变量间也存在一定的非线性关系。
。这也表明该数据中变量间也存在一定的非线性关系。
6. 结论
本文建立了非线性联合均值方差模型,主要研究了该模型中未知参数的极大似然估计,并介绍了极大似然估计中常用的迭代算法——Gauss-Newton迭代算法的具体实现步骤。模拟结果显示,通过GaussNewton迭代算法得到了较为满意的联合模型的参数估计结果,并且在实例分析中,对伦福德冷却实验数据和氟哌啶醇血浆浓度数据的应用也表明了该模型和所运用的方法是有用和有效的。另外在现实生活中,缺失数据也是经常碰到的复杂数据类型之一,以后可以运用合适的借补方法来研究分析缺失数据下非线性联合均值方差模型的统计推断问题。
基金项目
国家自然青年科学基金项目(11301485);浙江农林大学校科研发展基金人才启动项目(2013FR079);浙江农林大学创新创业训练计划(201311006)。
参考文献 (References)
- [1] White, H. (1980) A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Journal of the Econometric Society, 48, 817-838.
- [2] Andrews Donald, W.K. (1991) Heteroscedasticity and autocorrelation consistent covariance matrix estimation. Journal of the Econometric Society, 59, 817-858.
- [3] Smyth, G.K. (2002) An efficient algorithm for REML in heteroscedastic Regression. Journal of Graphical Statistics, 11, 836-847.
- [4] Park, R.E. (1966) Estimation with heteroscedastic error terms. Econometrica, 34, 888.
- [5] Harvey, A.C. (1976) Estimating regression models with multiplicative heteroscedasticity. Econometrica, 44, 460-465.
- [6] Aitkin, M. (1987) Modelling variance heterogeneity in normal regression using GLIM. Applied Statistics, 36, 332-339.
- [7] Verbyla, A.P. (1993) Modelling variance heterogeneity: Residual maximum likelihood and diagnostics. Journal of the Royal Statistical Society: Series B, 52, 493-508.
- [8] Wu, L.C. and Li, H.Q. (2012) Variable selection for joint mean and dispersion models of the inverse gaussian distribution. Metrika, 75, 795-808.
- [9] Xu, D.K., Zhang, Z.Z. and Wu, L.C. (2014) Variable selection in high-dimensional double generalized linear models. Statistical Papers, 55, 327-347.
- [10] 吴刘仓, 黄丽, 戴琳(2012) Box-Cox 变换下联合均值与方差模型的极大似然估计. 统计与信息论坛, 5, 3-8.
- [11] 马婷, 吴刘仓, 黄丽(2013) 基于偏正态分布联合位置, 尺度与偏度模型的极大似然估计. 数理统计与管理, 3, 433-439.
- [12] 徐登可, 张忠占, 张松, 张蕾 (2012) 妊娠期高血压疾病危险因素的统计分析. 应用概率统计, 2, 134-142.
- [13] 贝茨, 沃茨, 著, 韦博成, 等, 译 (1997) 非线性回归分析及其应用. 中国统计出版社, 北京.
