Statistics and Application
Vol.05 No.02(2016), Article ID:17917,12
pages
10.12677/SA.2016.52013
Fitting and Prediction of Multi Macroeconomic Time Series
—Based on VAR Model and State-Space Model
Jingru Yin
College of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming Yunnan

Received: Jun. 7th, 2016; accepted: Jun. 26th, 2016; published: Jun. 30th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Predictions have been concerned about the issue, especially in the macroeconomic. Univariate time series prediction can not meet basic needs. Multiple macroeconomic time series has urgent demand for reasonable model. Currently AR model and VAR model develop better, and to some extent, are used for analysis and policy analysis in macro fields. While state space model validates observable variables, unobserved variables are added. In an open economy and the rapid development background, state-space model can adapt to the actual needs. This paper selects the three basic macroeconomic variables in three areas (industrial, money supply and CPI), fitting VAR model and state space model and predicting, comparing predictions. The results show that the prediction accuracy of the state space model is superior to the VAR model.
Keywords:Prediction, State Space Model, VAR Model, Macroeconomic

多元宏观时间序列的拟合及预测
—基于VAR模型和状态空间模型
尹静茹
云南财经大学统计与数学学院,云南 昆明

收稿日期:2016年6月7日;录用日期:2016年6月26日;发布日期:2016年6月30日

摘 要
预测是一直以来关注的问题,尤其在宏观经济方面。单变量时间序列的预测已不能满足基本的需要,多元宏观经济时间序列对拟合合理的模型需求迫切,当下AR模型和VAR模型发展较为完善,在一定程度上用于宏观领域分析及政策分析。状态空间模型在验证可观测变量的同时,加入不可观测变量,在经济开放且发展迅速的前提下更能适应实际的需要。本文选取三个宏观经济中三个方面(工业,货币供给和CPI)的基本变量,拟合VAR模型和状态空间模型并进行预测,比较预测效果。结果表明,状态空间模型的预测精度要优于VAR模型。
关键词 :预测,状态空间模型,VAR模型,宏观经济

1. 引言
近几十年来,包含少量变量的小模型的计量运用进展很大。在平稳前提下,小宏观计量模型的估计、检验和推断形成了系统的理论和框架。尤其重要的是,Granger (1987)提出了协整理论,为多变量时间序列的建模拓展了空间,使得多变量时间序列建模中“变量是平稳的”假定不再是必须的;另一方面,Sims (1980)提出向量自回归模型(VAR模型),将单变量的自回归模型推广到多变量时间序列组成的向量自回归模型,从而VAR模型广泛的渗透到宏观分析的各领域,推动了经济系统动态性分析的运用,成为政策分析的有效工具。平稳VAR模型的估计和推断方法早已建立,而对VAR更为重要的识别理论也已发展地较为完善。并且在经验研究上,各地学者关于如何使用此类模型积累了很多的经验 [1] 。
在分析经济现象随时间变化规律的过程中,状态空间模型的优点是在验证可观测变量的同时,加入了不可观测变量 [2] 。状态空间模型可以表现出研究经济现象的状态随时间变动的规律,同时也可以判断所选择的状态是否能够反映观测变量的真实状况,并且在描述系统变化过程的前提下包含尽可能少的元素 [1] 。改革开放以来,我国经济发生了巨大的结构变化,开放经济下面临着各种政策变动影响、外界干扰等不可观测变量冲击,之前的一些实证方法并未考虑到这些问题,而状态空间模型可以很好地考虑和反映这些不可观测变量的影响 [2] 。
因此在本文关注的经济预测方面,我们进行了协整分析并进而构建VAR 模型和状态空间模型,预测结果进行比较。
2. 模型描述
2.1. 向量自回归(VAR)模型
Sims于1980年提出了向量自回归模型(简称VAR模型),VAR模型不以经济理论为基础,采用多方程联立的形式,在模型的每一个方程中,内生变量对模型的全部内生变量的滞后值进行回归,进而估计全部内生变量的动态关系。VAR模型常用于预测相互联系的时间序列系统,也常用于分析随机扰动对变量系统的动态冲击,进而解释各种经济冲击对经济变量形成的影响 [3] 。
VAR模型的一般形式为:
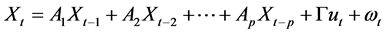 (1)
(1)
这里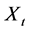 为
为 的内生变量,
的内生变量,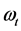 为同样维数的扰动项,
为同样维数的扰动项, 为
为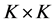 的系数矩阵,
的系数矩阵,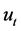 为外生变量,
为外生变量,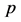 为滞后阶。模型中可以加常数项、趋势项,或者两者都加。
为滞后阶。模型中可以加常数项、趋势项,或者两者都加。
如果用滞后算子来表示 式则有:
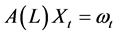 (2)
(2)
这里 。模型(2)式常称为VAR模型的简化形式,模型中的随机项常被称为“冲击向量”或“简化形式的冲击向量”或“信息向量”或“异常向量”。
。模型(2)式常称为VAR模型的简化形式,模型中的随机项常被称为“冲击向量”或“简化形式的冲击向量”或“信息向量”或“异常向量”。
VAR模型的特点有:首先,VAR模型不以经济理论为依据,在建模过程中只需要把那些相互有关的变量包括进VAR模型,同时确定滞后阶p即可;其次,VAR模型对待估计的参数施加零约束,即参数估计值不管显著与否,都保留在模型中;再次,VAR模型需要估计的参数较多,如一个含有三个变量,最大滞后期p = 3的VAR模型,有27个参数需要估计,所以当样本容量较小时,会严重影响VAR模型参数估计量的精度 [4] 。
关于模型的估计,通常采用OLS法或极大似然法进行估计,在估计前需要确定模型的滞后阶p。p值的选择可以利用LR统计量或者BIC,AIC和SC准则来确定。
2.2. 向量自回归移动平均(VARMAX)模型
在VAR模型,VARMAX模型(带有输入变量的向量自回归移动平均模型)的矩阵形式为:
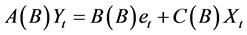 (3)
(3)
若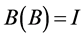 ,则为VARX模型:
,则为VARX模型:
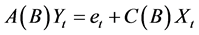 (4)
(4)
这里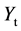 为k维输出变量,
为k维输出变量, 为m维输入变量,
为m维输入变量,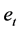 为不可观测的误差或扰动过程,B为后移算子。所以上述表达式(3)为带有输入变量的向量自回归移动平均模型。
为不可观测的误差或扰动过程,B为后移算子。所以上述表达式(3)为带有输入变量的向量自回归移动平均模型。
2.3. 状态空间模型
一般的线性正态状态空间模型为:
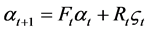 (5)
(5)
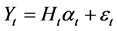 (6)
(6)
 (7)
(7)
这里方程(5)为状态方程,(6)为测量方程,(7)为初始状态向量的分布。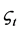 ,
,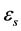 对所有t,s独立,并且独立于
对所有t,s独立,并且独立于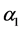 ,观测值
,观测值 可能是多维的,状态向量
可能是多维的,状态向量 是不可观测的。
是不可观测的。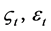 均服从正态分布。系数矩阵
均服从正态分布。系数矩阵 ,
,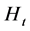 确定了模型的结构,它们可能包括了未知参数。
确定了模型的结构,它们可能包括了未知参数。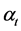 是一个向量自回归VAR(1)过程。
是一个向量自回归VAR(1)过程。
状态空间模型的各个成分都可加可减,进行各种变化,还可以加入非随机的输入项。由于其灵活性,状态空间模型用一种统一的方法包括了范围很广的多类模型及方法,诸如动态回归、ARIMA、不可观测分量模型、隐函数模型等。
这里使用线性的状态空间模型,因此关于多元正态分布的性质都成立,可以使用状态似然函数。关于状态空间模型的估计有两方面:一是度量不可观测的状态,包括预测、滤波及光滑;二是用最大似然法估计未知参数 [5] 。
3. 数据介绍
本文采用2005年1月到2015年11月跨度为131个月的月度数据,时间序列跨度较长,可以充分验证时间趋势。变量个数为三个,分别为工业增加值增长率,货币和准货币(M2)增速和居民消费价格指数(CPI)。
这三个变量反映宏观经济的基本面,并且相互影响,均采用增速,可避免量纲不同出现其他问题。货币供给变动选取广义货币(M2),这与之前一些文献选取狭义货币(M1)不同,广义货币M2既可以反映现实购买力,同时可以反映潜在购买力,它对于通货膨胀具有不可忽略的影响 [2] 。选用CPI能反映我国通货膨胀。本文数据均来自中经网数据库。
4. 实证检验
4.1. 数据描述
如图1和图2所示,从样本数据来看,M2增速从2005年一开始处于水平状态,小幅波动,从09年初到10年初经历了一个大幅度上升后下降的过程,而后保持相对水平,有小幅波动。CPI和CPI增速与M2增速保持同步相反方向变动。工业增加值增长率波动幅度较大,但整体趋势与M2增速相同。
4.2. 协整检验
4.2.1. 平稳性检验
变量序列平稳是构建VAR模型和状态空间模型的基础。我们考察三个变量的平稳性,采用KPSS单位根检验 [6] 。
KPSS单位根检验结果如下表1所示。
根据结果可以判断M2增速和工业增加值增速为一阶单整序列;CPI为水平平稳序列,但一阶差分后趋势平稳,故认为CPI为一阶单整序列。
4.2.2. 协整分析
本文中三个变量均为同阶单整时间序列,因此我们进行协整分析,运用Johansen协整检验,Engle-Granger协整检验和Granger因果检验。
Johansen协整检验结果如下表2、表3所示:(分别用迹检验和最大特征值检验)
(1) 迹检验的检验统计量和临界值的输出见表2。
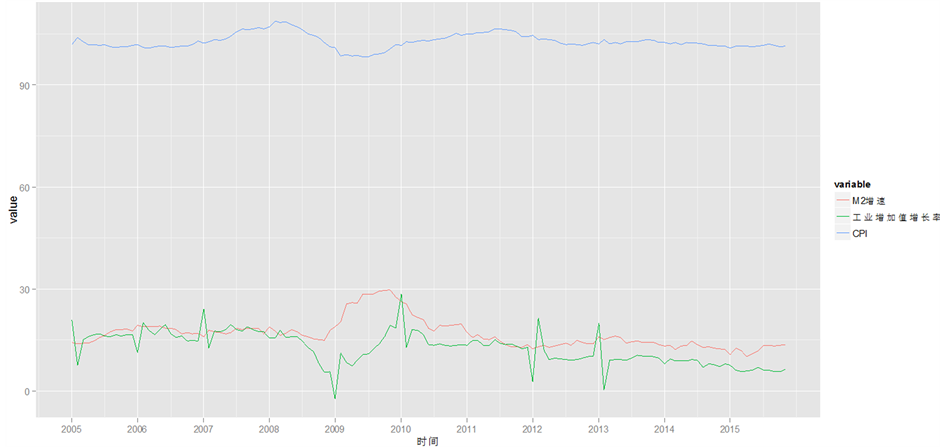
Figure 1. Trend chart of M2 growth, the growth rate of industrial added value and CPI
图1. M2增速,工业增加值增长率和CPI走势图

Figure 2. Trend chart of M2 growth, the growth rate of industrial added value and CPI growth
图2. M2增速,工业增加值增长率和CPI增速走势图
Table 1. KPSS test results
表1. KPSS单位根检验结果
Table 2. Values of trace test statistic and 10%, 5% and 1% critical values of test
表2. 迹检验的检验统计量和10%,5%和1%的临界值
这里对于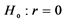 检验的 值小于0.01,而对于
检验的 值小于0.01,而对于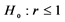 检验的 值大于0.1。
检验的 值大于0.1。
(2) 最大特征值检验的检验统计量和临界值的输出见表3。
因此这两个检验的结果基本一致,各变量在5%显著性水平上存在协整关系,均表明r = 1,存在一个协整向量。从协整关系结果来看,三个变量存在相互影响。
EG协整检验:我们针对数据中的三个变量轮流做因变量来进行回归,结果三个回归方程的p值均小于0.01,表示回归都是显著的,也就是说变量之间有显著的相关关系。进而检验残差是否是 (0)的。结果如下表4所示。
结果是显著的,三个回归方程的残差的检验统计量的值均小于5%的临界值,故拒绝有单位根的零假设,所以每个残差都是I(0)的。说明可能存在协整关系。
Granger因果检验:结果如下表5所示。
结果显示,p值都很小,均远小于0.05,但最显著的是工业增加值增长率->CPI和CPI->工业增加值增长率,说明工业增加值增长率和CPI互为“Granger原因”更明显。三个变量之间都有可能存在因果关系或者相互影响。
4.3. VAR模型
我们把三个变量都放入内生变量,模型中加上常数项和趋势项,滞后期取p = 2。时间取2005年1月到2014年12月。
Table 3. Values of eigen test statistic and 10%, 5% and 1% critical values of test
表3. 最大特征值检验的检验统计量和10%,5%和1%的临界值
这里对于 检验的 值小于0.05,而对于
检验的 值小于0.05,而对于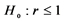 检验的 值大于0.1。
检验的 值大于0.1。
Table 4. The stability test of residuals of Engle-Granger test
表4. Engle-Granger协整检验中残差的平稳性检验
Table 5. Granger causality testing results
表5. Granger因果检验结果
输出结果用矩阵形式表示出拟合的模型为:(M2增速用X1表示,工业增加值增速用X2表示,CPI用X3表示)
 (8)
(8)
并且根据拟合的VAR模型预测未来10个月的预测图如下图3所示,并与真实值进行比较(图4)。
VAR模型对2015年10个月的预测值与真实值的比较如表6所示。
4.4. VARX模型
由前面可知,三个变量之间是相互影响的,我们任意选择X1(M2增速)作为输出变量,X2和X3作为输入变量进行拟合及预测。拟合出的模型结果为:
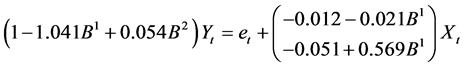 (9)
(9)
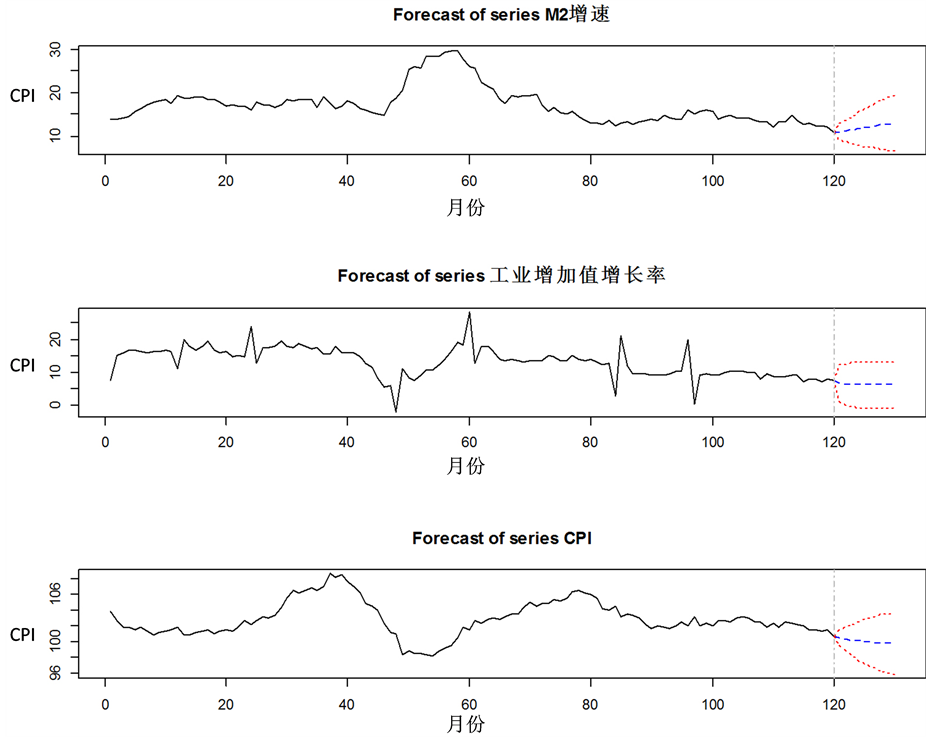
Figure 3. Using VAR model to fit the three variables (M2 growth, the growth rate of industrial added value and CPI) data and making predictions for the coming months
图3. 用VAR模型拟合三个变量(M2增速、工业增加值增长率和CPI)数据并对未来10个月做预测
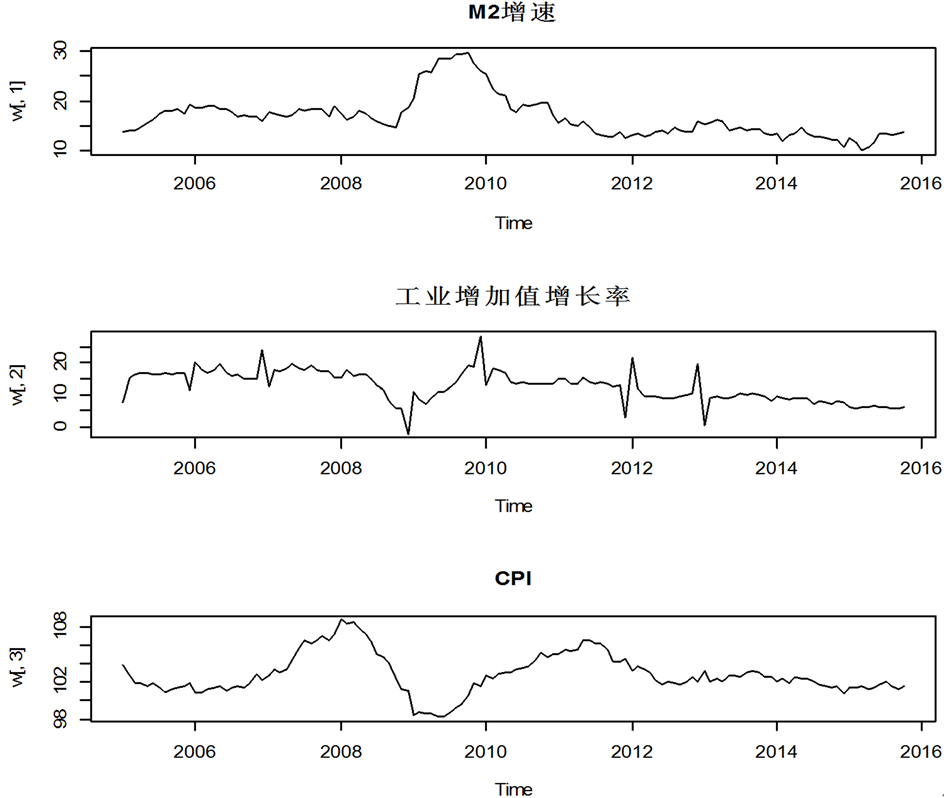
Figure 4. The real value of the three variables (M2 growth, the growth rate of industrial added value and CPI)
图4. 三个变量(M2增速、工业增加值增长率和CPI)数据的真实值
Table 6. VAR model predictions and the real value (January 2015-October 2015)
表6. VAR模型预测值与真实值(2015年1月~10月)
或者是
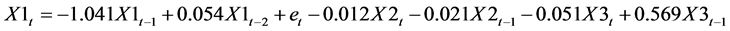 (10)
(10)
检验模型的稳定性及残差是否序列相关结果如图5所示,结果表明系统稳定,残差没有显现出序列相关。
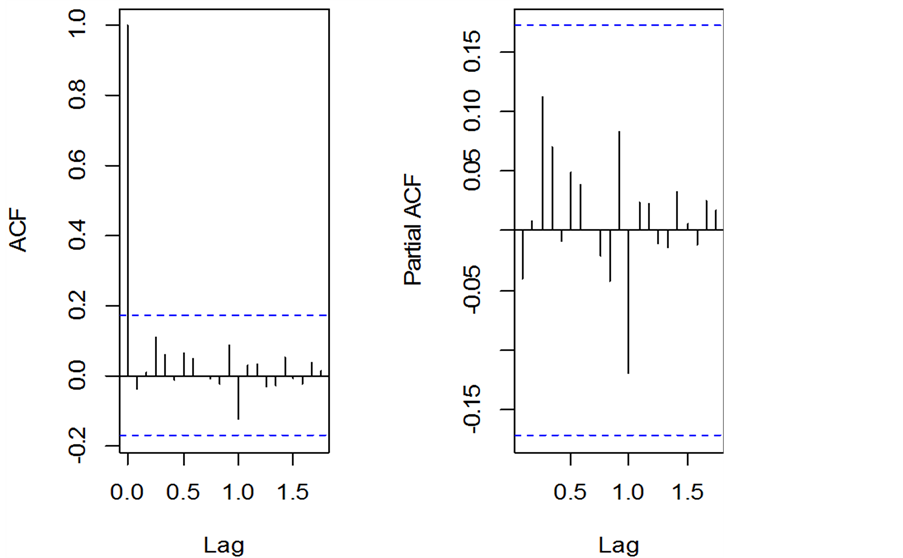
Figure 5. Acf diagram and pacf diagram of residuals of results using VARX model to fit the three variables (M2 growth, the growth rate of industrial added value and CPI) data
图5. 用VARX模型拟合三个变量(M2增速、工业增加值增长率和CPI)数据结果残差的acf图及pacf图
根据拟合的VARX模型进行预测,用2005年1月到2014年12月的数据预测2015年11个月的M2增速,再于2015年的真实值进行比较(图6)。
2015年1月到2015年11月的预测值如表7所示。
4.5. 状态空间模型
将三个变量引入状态空间模型并进行估计和预测,结果表明模型系统是稳定的(图7),残差没有显现出序列相关。
拟合的状态空间模型为:
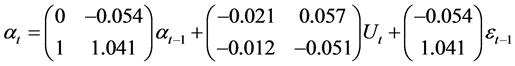 (11)
(11)
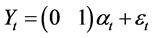 (12)
(12)
根据拟合的状态空间模型进行预测,用2005年1月到2014年12月的数据预测2015年11个月的M2增速,再于2015年的真实值进行比较。结果得到预测的结果和预测图与VARX模型得到的结果类似(表8)。
预测结果用均方误差判断:MSE(VAR模型) = 0.769;MSE(状态空间模型) = 0.7609。
结果表明,状态空间模型的预测比VAR模型更精确(图8)。
5. 结论
本文中三个宏观经济变量,分别为M2增速,工业增加值增长率和CPI,通过检验平稳性得出此多
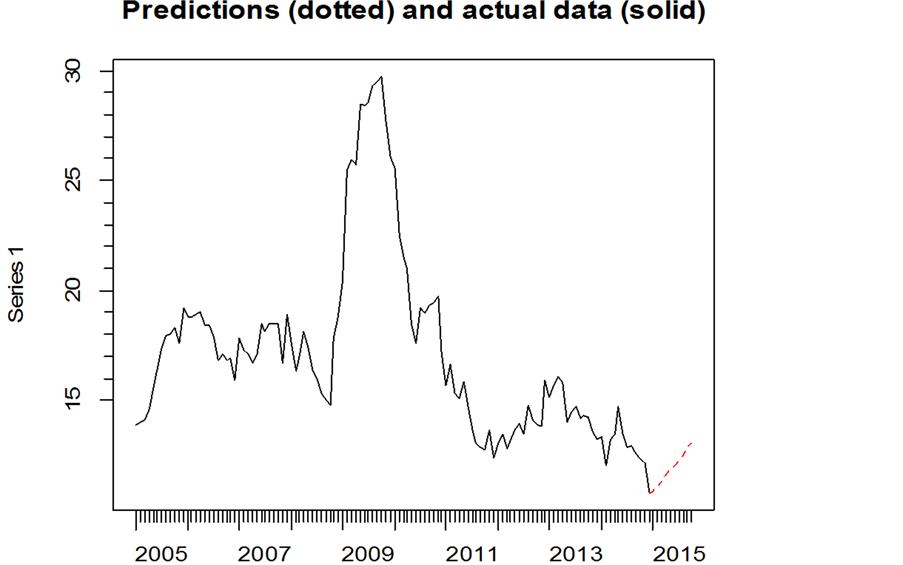
Figure 6. Predictive value of M2 growth (dotted line)
图6. M2增速的预测值(虚线)
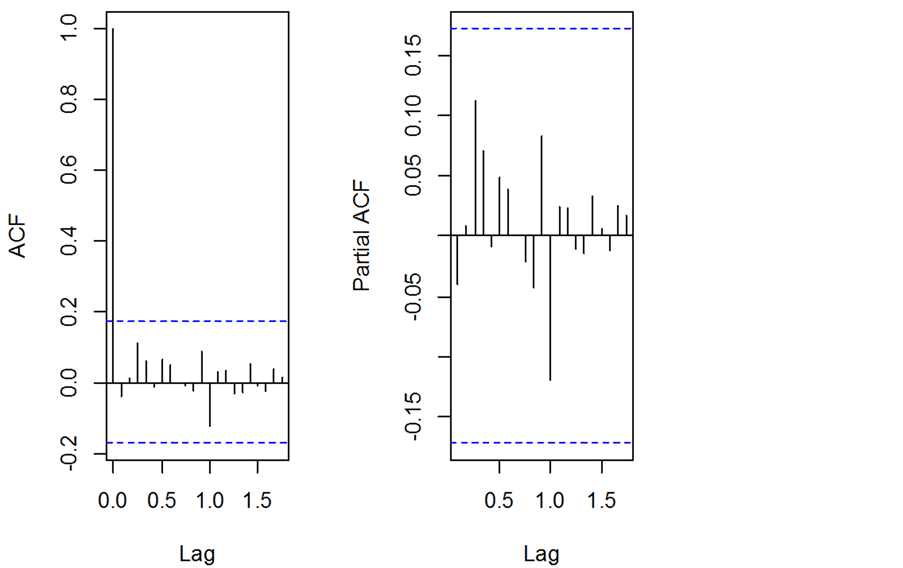
Figure 7. Acf diagram and pacf diagram of residuals of results using state space model to fit the three variables (M2 growth, the growth rate of industrial added value and CPI) data
图7. 用状态空间模型拟合三个变量(增速、工业增加值增长率和CPI)数据结果残差的acf图及pacf图
Table 7. VARX model predictions and the real value (January 2015-October 2015)
表7. VARX模型预测值与真实值(2015年1月~10月)
Table 8. State space model predictions and the real value (January 2015-October 2015)
表8. 状态空间模型预测值与真实值(2015年1月~10月)
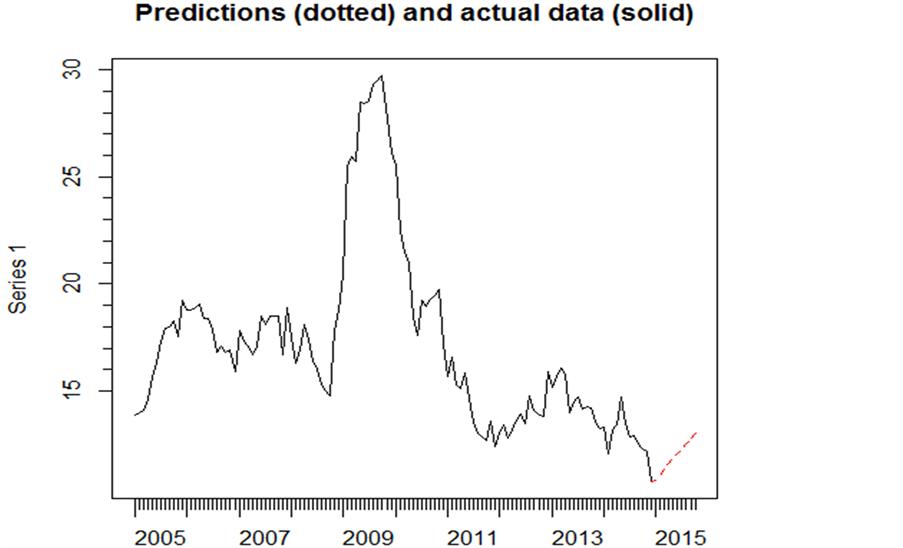
Figure 8. Predictive value of M2 growth (dotted line)
图8. M2增速的预测值(虚线)
元宏观经济变量是协整关系,进而拟合VAR模型和状态空间模型。两个模型拟合结果均是稳定的,但是
预测值有所差异,VAR模型的预测值不稳定,与真实值相差较大;状态空间模型的预测值与真实值相近,说明状态空间模型的理论适用于宏观经济的实证研究,更能反映实际经济活动。
文章引用
尹静茹. 多元宏观时间序列的拟合及预测—基于VAR模型和状态空间模型
Fitting and Prediction of Multi Macroeconomic Time Series—Based on VAR Model and State-Space Model[J]. 统计学与应用, 2016, 05(02): 136-147. http://dx.doi.org/10.12677/SA.2016.52013
参考文献 (References)
- 1. 朱满洲. 动态因子模型的理论和应用研究[D]: [博士学位论文]. 武汉: 华中科技大学, 2013.
- 2. 林博. 汇率波动、货币供给与通货膨胀——基于状态空间模型的实证研究[J]. 经济问题探索. 2015(4).
- 3. Stock, J.H. and Watson, M.W. (2010) Dynamic Factor Models. Oxford Handbook of Economic Forecasting.
- 4. 高铁梅. 计量经济分析方法与建模——EViews应用及实例[M]. 清华大学出版社, 2006.
- 5. 陈友春, 朱文婕. 状态空间模型及其在传染病发病率预测中的应用[J]. 南京医科大学学报(自然科学版). 2015, 35(2).
- 6. 吴喜之, 刘苗. 应用时间序列分析——R软件陪同[M]. 机械工业出版社, 2014.
