Statistics and Application
Vol.06 No.03(2017), Article ID:21644,9
pages
10.12677/SA.2017.63036
Multivariate Statistical Analysis and Prediction of PM2.5 Concentration in Xiamen
Xiaofen Xu, Qitong Ou
School of Applied Mathematics, Xiamen University of Technology, Xiamen Fujian
Received: Jul. 20th, 2017; accepted: Aug. 5th, 2017; published: Aug. 9th, 2017

ABSTRACT
In this paper, we use the statistical principle to analyze the factors influencing the concentration of PM2.5 in Xiamen daily in 2016, and use statistical software to test whether it has correlation at first. Then we use the method of multiple linear regression analysis to build reasonable mathematical model, to forecast the concentration of PM2.5 in Xiamen during January and February 2017. Finally, reasonable suggestions are put forward according to the prediction results.
Keywords:PM2.5, Multiple Stepwise Regression Analysis, Air Quality Index AQI, SPSS
厦门市PM2.5浓度的多元统计分析与预测
许晓芬,欧启通
厦门理工学院应用数学学院,福建 厦门
收稿日期:2017年7月20日;录用日期:2017年8月5日;发布日期:2017年8月9日

摘 要
本文首先运用统计学原理对厦门市2016年全年每日影响PM2.5浓度的因素进行整体分析,并且利用统计软件检验其是否具有相关性,然后采用多元线性回归分析的方法构建合理的数学模型,预测厦门市2017年1月和2月的PM2.5的浓度,最后结合预测结果提出了合理建议。
关键词 :PM2.5,多元线性回归分析,空气质量指数AQI,SPASS

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
我国在经济迅速发展的今天,许多环境问题相继而生,因此,进行环境治理势在必行。肖建能 [1] 结合厦门市土地利用分类专题图和主要重工业企业分布图进行厦门市环境空气质量状况污染源的分析。赵晨曦 [2] 和吴建南 [3] 通过对PM2.5的研究,分析 PM2.5与植被和雾霾的影响。本课题对厦门市往年空气中的PM2.5浓度进行研究和预测,以便于提前采取有效措施控制PM2.5的浓度,这可以为城市规划师和环保局治理空气中的污染成分提供依据。
厦门市未来PM2.5的浓度与其它空气质量检测指标PM10、NO2、SO2、CO、O3等因素相关,对以上指标做出合理的分析能够帮助我们准确预测PM2.5的浓度,更好地对厦门的空气质量进行改善。本文主要解决了以下几个问题:
1) 分析厦门市2016年AQI里的6个基本监测指标的相关性;
2) PM2.5的浓度变化受其他5个指标影响的显著性,建立回归模型,求出PM2.5与各变量的相关系数;
3) 利用搜集到的数据,以及对李子奈 [4] 、何晓群 [5] 和杨云 [6] 相关著作的研究,建立回归模型,对2017年前两个月PM2.5的浓度做线性回归进而完成预测。
2. 数据的收集和处理
为了分析和预测出厦门市PM2.5的浓度,我们从天气后报网和厦门市环保局收集到2016年厦门市空气质量指数和影响PM2.5浓度的其他指标的浓度日均值。利用日均值数据求出月均值如表1。
为了让结果更加直观的呈现出来,我们对PM2.5的月均值数据做了折线图,如图1。以便于进行整体上的初步分析,观察是否能寻找数据中隐藏的规律。由以下的图1容易发现的是其浓度在月份之间的变化范围很大,有明显的季节性变化。
厦门2016年PM2.5浓度的变化为5~10月浓度较低,3月登顶为40 μg/m3,几近年均值的1.5倍,3~6月急剧下降,6月达最低16 μg/m3,低于年均线。6~10月浓度均值相对较低且相差幅度小,全年PM2.5浓度没有明显变化势头,而是受季节影响,夏秋低,春冬高。
3. PM2.5浓度影响因素的相关性分析
从图1中可知3月PM2.5的浓度全年最高6月最低,我们就对3月和6月的数据进行分析和研究。为了检验这些因素是否能与PM2.5建立线性回归模型,根据相关分析方法判断这些因素与PM2.5的浓度值是否具有相关性。首先采用皮尔逊相关系数法来检验变量的相关性,运用软件SPSS容易获得3月份6个监测指标的相关系数的数据如表2。
由表2可知,3月PM2.5与空气质量指数AQI具有很强的相关性,且各指标中PM2.5乃威胁空气质量的重大因素,其相关系数达0.996,PM2.5与PM10、NO2、SO2之间明显有着强相关性,而对于臭氧
Table 1. 2016 Air Quality Index and Monthly Mean of 6 Indicators (μg/m3)
表1. 2016年空气质量指数及6项指标的月均值(μg/m3)
Table 2. Pearson correlation coefficients for each indicator in March
表2. 3月份各指标的Pearson相关系数
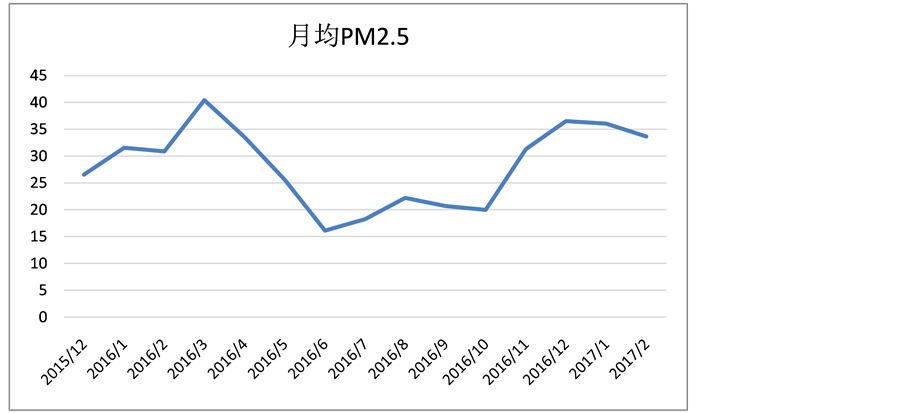
Figure 1. The monthly mean change of PM2.5 concentration
图1. PM2.5浓度的月均值变化线图(μg/m3)
和CO则相关性非常弱,不同的污染物浓度之间的相关性分析可以作为构建PM2.5浓度的预测模型提供有力的理论支撑。
基于2016年6月份的污染物浓度监测数据进行分析,运用软件SPSS容易获得6个监测指标的相关系数的数据如表3。
由表3可以看出,6月份PM10成为AQI的主要影响成分,PM2.5与每个指标都具有强相关性,与表2所分析出的内容产生了一定的矛盾。由此,受季节性变化和诸多未知因素的共同影响,PM2.5浓度在月份之间的波动范围甚大,单纯对某一月份进行分析会造成很大的误差。
为了减少外界因素对结果造成的误差,我们不采用某些月份来研究,而是基于2016年366天的污染物浓度监测数据进行分析,用软件SPSS得6个监测指标的相关系数如表4。
由表4可以看出,除了O3与PM2.5的相关性不算太强以外,PM2.5与其他指标都显示有强相关性。
为了提高相关分析结果的准确性,本文接下来运用另一种分析方法——方差分析。从观测变量的方差着手,研讨各种控制变量中多少变量是对观测变量起到明显作用的变量。运用SPSS软件可以得出如图2所示的几个单因素方差分析表的缩略图。
由图2可以得出以下结论:PM2.5与PM10、NO2、SO2、CO和O3方差分析的P值均小于系统设定0.05的显著性水平,表明以上因素对厦门市大气中PM2.5浓度值的变化存在显著性,所研究变量的相关性检验通过。
4. 多元线性回归模型
综合以上相关分析的结果,对于厦门市2016年影响PM2.5浓度的要素分析,主要考虑以下5个因素PM10、NO2、SO2、CO、O3的影响,且已满足多元线性回归模型的条件,只要数据准确无误,便可以着手构建模型。
多元线性回归模型,通常形式为:

其中 即PM2.5,
即PM2.5,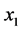 为自变量PM10,
为自变量PM10,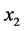 为NO2,
为NO2, 是SO2,
是SO2, 为CO,
为CO,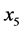 为O3,
为O3, (
(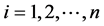 )称为回归系数,可称上式为总体回归函数的随机表达式。
)称为回归系数,可称上式为总体回归函数的随机表达式。
将搜集到的数据代入回归模型计算变量的回归系数,运行SPSS软件得到如下结果:
表5中B代表各项自变量的系数,系数B的置信区间中,变量 (NO2)过了0点,说明其系数取值在正负之间摆动,没达到预测效果,且表中NO2的P值大于显著性水平0.05,故该变量不适合作回归分析。在满足构建模型的情况下,造成以上结果很可能源于数据存在异常值或者异方差性。
(NO2)过了0点,说明其系数取值在正负之间摆动,没达到预测效果,且表中NO2的P值大于显著性水平0.05,故该变量不适合作回归分析。在满足构建模型的情况下,造成以上结果很可能源于数据存在异常值或者异方差性。
首先我们进行的是检验数据是否存在异常值。回归分析中,搜集的数据常出现一些异常或极端的值,极大地影响拟合效果,一元线性回归可用简单的残差图或散点图来识别,本文的多元线性回归采用库克距离(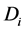 )来识别,判别标准为:若
)来识别,判别标准为:若 < 0.5时,是非异常值点;
< 0.5时,是非异常值点; > 1便是异常值点。用软件计算结果如下图:
> 1便是异常值点。用软件计算结果如下图:
由图3可以看出第53行数据的库克距离(表中COO_1列)大于1,我们将这行异常数据剔除后再计算一次库克距离后的结果显示库克距离全部小于1,那么异常值已经剔除了,可以进行拟合,拟合结果如表6。
由表6可知变量 (NO2)系数的P值为0.747,剔除异常值后依然没有通过显著性检验,所以对回归模型计算出错的原因不是因为数据存在异常值。
(NO2)系数的P值为0.747,剔除异常值后依然没有通过显著性检验,所以对回归模型计算出错的原因不是因为数据存在异常值。
接下来,本文改斯皮尔曼等级相关系数法来检验数据的异方差性,其应用更广泛,可用于线性也可
Table 3. Pearson correlation coefficients for each index in June
表3. 6月份各指标的Pearson相关系数
Table 4. Pearson correlation coefficients for each indicator in 2016
表4. 2016年各指标的Pearson相关系数

Figure 2. Single factor analysis of variance
图2. 单因素方差分析结果
Table 5. Calculation of regression model coefficients
表5. 回归模型系数计算
Table 6. Calculate the regression model coefficients after rejecting the outliers
表6. 剔除异常值后的回归模型系数计算

Figure 3. Cook distance
图3. 库克距离
用于非线性的情况。使用软件对已有数据进行Spearman测验,结果如表7。
由表7可知变量PM10、O3与残差绝对值(abs)都出现显著相关现象,表明数据存在异方差。
当一个回归问题有了异方差性时,普通最小二乘估计的有效性已被破坏。对于异方差的修正我们用加权最小二乘估计法,再次利用斯皮尔曼相关系数法检验出与PM2.5具有强相关性的自变量为PM10,我们令PM10做权变量,利用加权最小二乘估计,结果如表8。
从表8能够直观地看出各个变量的P值都是0,小于显著性水平0.05,表明能够继续对数据进行拟合。综上可得线性回归模型:
 .
.
最后,为了进一步确认上述加权回归模型的可靠性,我们还需要对模型进行显著性测验,借助软件可以得到结果如表9,表10。
Table 7. Spearman rank correlation coefficients
表7. Spearman等级相关系数
Table 8. Weighted least squares estimation regression coefficients
表8. 加权最小二乘估计回归系数
Table 9. The test of R2
表9. R2检验
Table 10. The variance homogeneity of F test
表10. 方差齐性F检验
1) 在拟合前,由统计软件可计算得R2 = 0.918,表9显示拟合之后R2 = 0.999,相差甚大,可见自变量与因变量之间的相关性极高,说明模型拟合比原模型好;
2) 方差齐性分析中的计算概率为0,小于显著性水平0.05,说明上述加权多元回归模型有效。
Table 11. The comparison of PM2.5 actual value and the predicted value
表11. PM2.5实际值与预测值的对比

Figure 4. Comparison of actual and predicted values
图4. 实际值与预测值对比图
5. PM2.5浓度的预测
本论文最重要的目的就是预测PM2.5的浓度,利用已有数据和已经建立的模型,预测2017年1月~2月的PM2.5浓度,结果如下:
由表11可知PM2.5的预测值与真实值,可能有几个稍有偏离的数据,整体上不会有太大区别,为保证模型和方法的合理性,并且更直观地对两者进行比较,我们通过线性拟合来判读计算出的数据是否正确、合理。
由图4可见拟合效果还算不错,预测值与实测值的数据相对统一,预测值为峰值时实际值也几乎达到峰值,说明预测结果与实际值的变化趋势相类似,故也又深入一层检验本文运用模型的准确性,对现今大气中PM2.5的预测具备极好的实践意义。
6. 结论
从2017年1月和2月厦门市PM2.5浓度的预测值中可以看出其浓度并未呈现稳定的上升还是降低的趋势,一样随着季节的变化在波动,可知 PM2.5浓度的变化是一个非平稳的具有周期变化的时间序列。但是厦门的地理位置优越,空气质量的级别都属优良,不会影响到人类的正常户外活动。但PM2.5是严重影响空气质量的成分,对PM2.5的预测对于空气治理和人类的健康生活都具有很大的促进作用。PM2.5的治理除了控制相关影响因素的浓度以外,最大的治理方式就是控制其污染源,而PM2.5的来源主要是机动车的直接和间接排放、煤炭的污染、工业的喷涂、城市的扬尘污染、农村的秸秆焚烧、还有燃料的燃烧等人为活动。对于其治理有如下几个意见:
1) 积极响应国家“去产能”的号召,淘汰掉落后的产能。
2) 推动各产业的结构化调整和技术创新,对扬尘和工业污染进行综合治理。
3) 严格施行单双号车限行制度,增加大排气量车购置税,控制机动车尾气排放。
4) 对厦门不同区域的植被结构进行不同设置,合理高效地利用生态绿化消除PM2.5.
5) 根据不同阶段的气候特征对PM2.5采取不同的治理措施。
文章引用
许晓芬,欧启通. 厦门市PM2.5浓度的多元统计分析与预测
Multivariate Statistical Analysis and Prediction of PM2.5 Concentration in Xiamen[J]. 统计学与应用, 2017, 06(03): 311-319. http://dx.doi.org/10.12677/SA.2017.63036
参考文献 (References)
- 1. 肖建能, 杜国明, 施益强, 等. 厦门市环境空气污染时空特征及其与气象因素相关分析[J]. 环境科学学报, 2016(9): 3363-3371.
- 2. 赵晨曦, 王玉杰, 王云琦, 等. 细颗粒物(PM_(2.5))与植被关系的研究综述[J]. 生态学杂志, 2013(8): 2203-2210.
- 3. 吴建南, 秦朝, 张攀. 雾霾污染的影响因素: 基于中国监测城市PM2.5浓度的实证研究[J]. 行政论坛, 2016(1): 62-66.
- 4. 李子奈, 潘文卿. 计量经济学(第三版) [M]. 北京: 高等教育出版社, 2006.
- 5. 何晓群, 刘文卿.应用回归分析(第四版) [M]. 北京: 中国人民大学出版社, 2015.
- 6. 杨云, 付彦丽. 关于空气中PM2.5质量浓度预测研究[J]. 计算机仿真, 2016(3): 413-418.
