Statistics and Application
Vol.07 No.01(2018), Article ID:23701,7
pages
10.12677/SA.2018.71005
Semi-Parametric Statistical Analysis of Air Pollution and Respiratory Diseases
Yanyong Zhao1, Yuan Liu1, Hongxia Hao2, Zhiyang Yao1
1Institute of Statistics and Big Data, Nanjing Audit University, Nanjing Jiangsu
2School of Mathematics, Southeast University, Nanjing Jiangsu

Received: Jan. 17th, 2018; accepted: Jan. 31st, 2018; published: Feb. 7th, 2018

ABSTRACT
The article mainly focuses on the relationship between the air pollution and diseases in respiratory system in Hong Kong based on the principal component dimensionality reduction method and partially linear models. In the empirical analysis, by comparing with the linear model and linear model with time, we find that the proposed method has a better predictive effect and the relationship between air pollution and respiratory diseases in Hong Kong is nonlinear.
Keywords:Air Pollution, Respiratory Diseases, Partially Linear Models
空气污染与呼吸疾病的半参数统计分析
赵彦勇1,刘原1,郝红霞2,姚志扬1
1南京审计大学,统计科学与大数据研究院,江苏 南京
2东南大学,数学学院,江苏 南京
收稿日期:2018年1月17日;录用日期:2018年1月31日;发布日期:2018年2月7日

摘 要
本文基于主成分降维方法和部分线性模型研究了香港地区的空气污染和呼吸疾病之间的关系。实证分析中通过与线性模型和带时间趋势的线性模型的对比研究,发现所提出的方法在预测效果上更加准确,并且香港地区的空气污染与呼吸疾病之间存在非线性关系。
关键词 :空气污染,呼吸疾病,部分线性模型

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来,空气污染愈发严重,人类对环境的破坏与污染让我们赖以生存的地球遭受侵害。空气污染对人类的直接影响便是通过人类的呼吸,继而引发各种呼吸疾病,并且这些呼吸疾病大多会导致各种难以想象的严重后果。研究可以发现,空气污染跟与呼吸道有关的呼吸疾病的发生率存在重要联系;同时,空气中蕴含的各种可以吸入的颗粒物的存在也会致使呼吸的困难和呼吸道的感染。如何有效地研究空气污染跟与呼吸道有关的呼吸疾病的发生率之间的关系成为众人关心的问题。
在过去20年中,关于半参数模型的估计和建模问题已引起了学者们的广泛关注。部分线性模型是其中一类简单有效的半参数模型,相对于参数和非参数模型,它有更强的适应性和解释能力,在医学、金融、环境等领域得到了广泛的认可。部分线性模型最早由Engle等 [1] 研究气象与电力问题时提出。在实际应用研究中使用部分线性模型或者对它进行各种相关研究的学者众多。Cuzick利用渐近估计方程研究其参数估计,得到了估计量的相合性 [2] 。梁华和黄四民基于部分线性模型对居民消费结构进行了剖析 [3] 。Schmalensee和Stoker使用它研究了美国家庭的汽油消费情况 [4] 。Liang等基于bootstrap方法研究了模型参数和误差方差的估计,发现利用bootstrap方法逼近得到的估计量与大样本估计量有相同的渐近分布 [5] 。在对异方差部分线性模型进行探讨时,Ma等证明了异方差下部分线性模型的参数是半参有效的 [6] ;You 和Chen研究了带有序列相关误差的半参数部分线性模型,给出了一种新的估计误差结构的方法,进一步提出窗宽选择方法、参数部分的有效半参广义最小二乘估计方法和基于bootstrap的拟合优度检验 [7] 。李启华等灵活运用模型了半参数形式下的特征价格指数 [8] 。Jiang基于调整参数指数平方损失函数提出了部分线性模型的稳健估计方法,并将其应用于研究花粉水平数据和盐分数据 [9] 。
协变量维数较高时,部分线性模型的估计效率会降低。杨宜平等 [10] 、Luo和Gerard [11] 提出了部分线性模型的变量选择方法,首先对高维协变量降维,再利用选择的协变量估计模型,有效提高了其估计精度。但是,该方法在实际应用中却较为复杂。因此,在前人研究的基础之上,本文从估计和预测的角度对维数较高的部分线性模型的估计进行探讨,拟将主成分分析方法应用到部分线性模型中,降低模型维数,提高模型的估计精度。为研究空气污染和呼吸疾病之间的相互关系,本文利用香港新东方东地区2000年1月1日至2001年1月15日的化学污染物水平与呼吸系统疾病每日住院人数数据,基于部分线性模型研究两者之间的关系。
本文的主要研究框架如下:第一部分,在部分线性模型基础上,提出了主成分部分线性模型,并对其估计方法进行介绍。第二部分是实证分析,将采用主成分分析与部分线性模型拟合和预测香港新东方东地区呼吸系统疾病每日住院人数,并通过比较得出结论。第三部分是本文的结论。
2. 模型的估计
部分线性模型中既包含参数部分又包含非参数部分,它具有超越参数和非参数模型的适应和解释能力,其具体形式为:
(1)
其中 是响应变量, 是 维参数向量, 是 维协变量, 是1维协变量, 是未知函数, 为随机误差,且满足 和 。
部分线性模型的估计方法有很多,如局部多项式估计、核估计、样条估计等。这里仅对局部多项式估计方法进行介绍。假设 是来自模型(1)的一组样本,有 。 鉴于真值 的一个非参数估计为
(2)
其中 , , , 为带宽。为了估计 ,最小化下面的残差平方和
(3)
求解式(3)的极小值,可得参数 的估计
(4)
其中 , , , , 。
基于估计的 ,可得非参数部分 的估计,即
(5)
3. 空气污染与呼吸疾病数据的实证分析
本部分利用香港某地区实际数据来探讨空气污染与呼吸疾病之间的关系。使用的实际数据是2000年1月1日至2001年1月15日的香港新东地区的空气污染物和其它影响环境因素的日常测量值数据,其中2000年2月19日到2000年2月24日的相对湿度由于数据缺失,剔除这七天的数据。主要考虑四种环境污染物——二氧化硫SD(g/m3)X1、可吸入颗粒物RSP(g/m3)X2、二氧化氮ND(g/m3)X3、臭氧OZ(g/m3)X4和两个环境因素——温度Tem(摄氏)X5和相对湿度Humi(%)X6。感兴趣的问题是研究新东地区的化学污染物与呼吸系统疾病每日住院人数(Y)之间的关系。
首先,将数据分为两部分,第一部分用于拟合模型,第二部分用于评价拟合的模型,数据的分割点是2001年1月1日。评价模型优劣的两个指标选用平均平方误差(MSE)和平均绝对误差(MAE),即
和 (6)
其中 是 的预测或拟合值, 是样本数。
简单统计分析发现,自变量X1、X2、X3、X4、X5、X6对Y的关系均是非线性的,因此考虑对X1、X2、X3、X4、X5、X6做主成分分析。前三个主成分的方差累积贡献率为82%,成分得分系数矩阵见表1。从而,三个主成分可表示为:
。
主成分Z1、Z2和Z3的方差累积贡献率为82%,包含了数据绝大部分的有用信息。数据由六个自变量变为三个自变量,达到降维目的。新的自变量Z1、Z2和Z3对呼吸疾病日住院人数(Y)的散点图如图1~图3所示。由图可知,呼吸疾病日住院人数(Y)与第一主成分Z1之间没有明显的线性关系,而与第二、第三主成分Z2、Z3之间存在较为明显的线性关系。所以,将Z1作为模型(1)中非参数部分的协变量,将Z2、Z3作为部分线性部分的协变量。基于新协变量Z1、Z2、Z3对模型(1)进行拟合和预测。
对于部分线性模型,先通过主成分方法降维,再计算回归系数,得 。图4给出了呼吸疾病日住院人数(Y)的真实值与估计值(data 1是真实值,data 2是估计值)。通过图4可知,使用所提出方法估计的呼吸疾病日住院人数(Y)接近其真实值,这说明提出的估计方法是非常有效的。最后,给出残差序列的散点图和自相关系数图,如图5和图6所示。通过图6可知,残差序列仅在滞后5阶时存在微弱的相关性,这进一步说明使用主成分降维方法和部分线性模型处理此数据是合理正确的。
接下来,利用部分线性模型对2001年1月1日到1月15日的呼吸疾病日住院人数进行预测。计算得到的预测值(四舍五入)为185、71、84、97、101、41、85、73、88、70、62、77、84、134、50,实际
Table 1. Component score coefficient matrix
表1. 成分系数得分矩阵

Figure 1. Z1 versus daily number of hospitalized patients with respiratory disease (Y)
图1. Z1对呼吸疾病日住院人数(Y)

Figure 2. Z2 versus daily number of hospitalized patients with respiratory disease (Y)
图2. Z2对呼吸疾病日住院人数(Y)
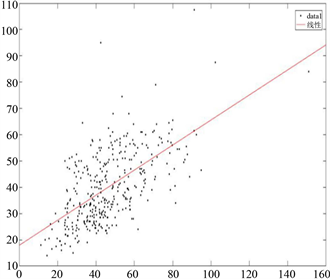
Figure 3. Z3 versus daily number of hospitalized patients with respiratory disease (Y)
图3. Z3对呼吸疾病日住院人数(Y)

Figure 4. True and estimated values for daily number of hospitalized patients with respiratory disease
图4. 呼吸疾病日住院人数(Y)的真实值和估计值
真实值为185、71、84、97、101、41、85、73、88、71、62、77、84、134、50,误差约为6.7%。一般情况误差小于10%认为预测是比较准确的。为了说明提出方法的优越性,再利用线性模型(LRM)和带有时间趋势的线性模型(LRMT)对此数据研究。表2列出了三种不同模型下计算的预测值的MSE和

Figure 5. Scatter graph of residuals
图5. 残差序列散点图
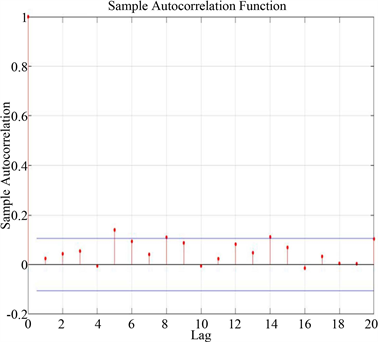
Figure 6. Autocorrelation function graph of residuals
图6. 残差序列自相关图
Table 2. MSE and MAE of daily number of hospitalized patients with respiratory disease
表2. 呼吸疾病日住院人数的MSE和MAE
MAE。通过表2可知,利用主成分降维方法和部分线性模型预测的结果明显比另外两种模型的预测更准确。
4. 结论
本文将主成分降维方法引入部分线性模型的估计,通过实证分析从系数估计和平均平方误差的角度,研究部分线性模型对建模香港地区空气污染与呼吸疾病数据的有效性。通过比对部分线性模型、线性模型和带有时间趋势的线性模型对实际数据的分析,验证了基于主成分降维方法的部分线性模型的预测结果更加准确和有效。同时,实证分析显示香港地区的空气污染与呼吸疾病之间存在非线性关系。
基金项目
国家自然科学基金项目(11701286、11571073);江苏省自然科学基金项目(BK20171073, BK20141326);江苏省教育厅高校哲学社会科学基金项目(2017SJB0350);江苏省高等学校自然科学研究项目资助(17KJB110006);江苏高等院校优先学科发展规划。
文章引用
赵彦勇,刘原,郝红霞,姚志扬. 空气污染与呼吸疾病的半参数统计分析
Semi-Parametric Statistical Analysis of Air Pollution and Respiratory Diseases[J]. 统计学与应用, 2018, 07(01): 32-38. http://dx.doi.org/10.12677/SA.2018.71005
参考文献 (References)
- 1. Engle, R.F., Granger, W.J., Rice, J. and Weiss, A. (1986) Serniparametric Estimates of the Relation between Weather and Elec-tricity Sales. Journal of the American Statistical Association, 80, 310-319. https://doi.org/10.1080/01621459.1986.10478274
- 2. Cuzick, J. (1992) Semiparametric Additive Regression. Journal of the Royal Statistical Society, Series B, 54, 831-843.
- 3. 梁华, 黄四民. 用半参数部分线性模型分析居民消费结构[J]. 数量经济技术经济研究, 1994(10): 33-35.
- 4. Schmalensee, R. and Stoker, T.M. (1999) Household Gasoline Demand in the United States. Econometrica, 67, 645-662. https://doi.org/10.1111/1468-0262.00041
- 5. Liang, H., Hardle, W. and Sommerfeld, V. (2000) Bootstrap Approximation in a Partially Linear Regression Model. Journal of Statistical Planning and Inference, 91, 413-426. https://doi.org/10.1016/S0378-3758(00)00191-9
- 6. Ma, Y.Y., Chiou, J.M. and Wang, N. (2006) Efficient Semiparametric Estimator for Heteroscedastic Partially Linear Models. Biometrika, 93, 75-84. https://doi.org/10.1093/biomet/93.1.75
- 7. You, J. and Chen, G. (2007) On Inference for a Semiparametric Partially Linear Regression Model with Serially Correlated Errors. The Canadian Journal of Statistics, 35, 515-531. https://doi.org/10.1002/cjs.5550350404
- 8. 李启华, 蓝志青, 等. 基于半参数估计的笔记本电脑特征价格指数研究[J]. 东北财经大学, 2011(2): 84-85.
- 9. Jiang, Y. (2015) Robust Estimation in Partially Linear Regression Models. Journal of Applied Statistics, 42, 2497-2508. https://doi.org/10.1080/02664763.2015.1043862
- 10. 杨宜平, 薛留根, 王学娟. 高维部分线性模型中的变量选择[J]. 北京工业大学学报, 2011, 37(2): 291-295.
- 11. Luo, J. and Gerard, P. (2013) Using Thresholding Difference-Based Estimators for Variable Selection in Partial Linear Models. Statistics and Probability Letters, 83, 2601-2606. https://doi.org/10.1016/j.spl.2013.08.011
