Statistics and Application
Vol.
07
No.
06
(
2018
), Article ID:
27986
,
8
pages
10.12677/SA.2018.76070
Statistical Diagnostics for Nonlinear Models with Right-Censored Data
Zhong Cheng, Yu Feng
School of Science, Nanjing University of Science and Technology, Nanjing Jiangsu

Received: Nov. 20th, 2018; accepted: Dec. 6th, 2018; published: Dec. 13th, 2018

ABSTRACT
This paper considers how to solve statistical diagnosis problem of the nonlinear models with right-censored data. First, we use the method of maximum likelihood estimates to reach the parameters. Based on the idea of case-deletion models, we obtain the formula of the parameters and propose some diagnostic statistics to determine outliers or influential points. Finally, we use numerical simulation analysis to verify the feasibility of the theory.
Keywords:Nonlinear Model, Right-Censored Data, Statistical Diagnostics, Case-Deletion Model, Generalized Cook Distance
非线性模型在右删失数据下的统计诊断
程忠,冯予
南京理工大学,理学院,江苏 南京

收稿日期:2018年11月20日;录用日期:2018年12月6日;发布日期:2018年12月13日

摘 要
本文研究了非线性模型在带有右删失数据下如何统计诊断的问题。首先用极大似然估计的方法求出了参数的估计问题。再对模型运用数据删除思想进行考量,求出了删除前后参数的公式,给出了判定影响点和异常点的一些统计量。最后,通过数值模拟分析,证明了该方法的可行性。
关键词 :非线性模型,右删失数据,统计诊断,数据删除模型,广义Cook距离

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
统计诊断 [1] 是数据分析的重要组成部分,其主要任务就是通过诊断统计量检测已知观测数据在既定模型拟合时的合理性,数据删除法 [2] 是其最基础的方法,即考虑删除前后统计量的变化。非线性模型 [3] 可以结合不同的数据类型进行研究,包括纵向数据、删失数据 [4] 等,最近一段时机在纵向数据下运用比较广,但关于删失数据则很少。右删失数据也是生存分析 [5] 尤其是在寿命观测中很常见的一种数据。本文考虑了带右删失数据下非线性模型的统计诊断问题 [6] ,有一定的理论和实践价值。
2. 右删失数据下非线性模型的参数估计
2.1. 右删失数据下的非线性模型
给定观测数据 ,非线性回归模型表示为 , ,其中 为参数 的非线性函数, 为未知的回归系数向量, 为随机误差。通常假定序列 独立正态同分布,其均值为0,方差为 。该模型的矩阵形式可表示为 ,其中 , , 。
因为 右删失,不失一般性,我们考虑前r个为由于试验的终止却未寿终数据,即 为右删失数据。由于有删失数据存在,因此需要求出新的似然函数来进行参数估计。
2.2. 右删失数据下的似然函数
设 是来自分布G的随机变量,并且独立同分布,其概率密度函数为 , 为模型参数。同时假设右删失时间 ,分布为F。假设 和 相互独立,记 , ,实际观察样本为 ,则右删失数据下的似然函数 [7] 为
(1)
2.3. 模型的极大似然估计
令 ,它是标准正态分布的概率密度函数。记 , , , 。则根据(1)式,模型的联合似然函数可表示为 ,取对数,得对数似然函数为
(2)
(2)式对 求导,可得
(3)
其中, ,记
参数的极大似然估计记为 ,此文利用高斯-牛顿迭代法求解。在此之前,先引进如下符号:
其中, , 为 阶矩阵, 为 阶立体阵。 为n阶对角阵。
引理1:对于右删失的非线性模型,Y关于参数的 的Score函数、观察信息阵以及Fisher信息阵分别为:
(4)
(5)
(6)
证:由(3)即可得 ,即(4)式得证。
对(3)式继续求导可得
即得(5)式。
由于 ,因此可得(6),证毕。
将以上结果代入高斯-牛顿迭代公式 可得
3. 模型诊断
3.1. 数据删除模型
数据删除模型是最基本的统计诊断模型,比较第i个点 删除前后估计量或统计量之间差异,其中i的取值范围为 。其中,本文只考虑删除完整的数据部分,对于由于右删失得到的数据点不研究异常或强影响点问题 [8] 。
于是,右删失下非线性模型的数据删除模型可表示为 ,其中 为右删失数据, 为完整值。其相应的极大似然估计记为 。
通常可由 的一阶近似公式来比较数据删除前 和删除后 的差异,即
(7)
其中 和 是 和 删除第i点以后得到的矩阵,而 是 删除第i点以后的向量。由引理1可知:
(8)
(9)
其中 为 删除第i行以后的 矩阵, 为 删除第i点以后的 维向量。
定理 对于右删失下非线性模型, 的一阶近似可表示为
(10)
其中, 表示D的第i个行组成的p维向量, 为矩阵 的第i个对角元。
证明:将(8)、(9)式代入(7)式可得
其中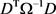 可进行以下分解:
可进行以下分解:
因此有 ,同理可得 。
这些公式代入以上 的表达式可得
应用矩阵和式求逆公式 ,
取 ,所以
由于 。
因此,当 时,
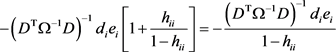 。
。
所以,
证明完成。
以上定理解出来了数据删除前和删除后估计量之间的数学公式,由此公式出发还能得到许多其他的估计量。这个公式表明如果 与 之间应相差很大,则说明i可能为异常点或强影响点。
3.2. 统计诊断量
3.2.1. 广义Cook距离
根据公式(10),我们即可得到 。在一般的回归模型中,Cook已经提出了Cook距离,因此这里我们将Cook距离推广到带删失数据的非线性模型中。广义Cook距离定义为
其中,M为正定矩阵; 为尺度因子。此处取为
则可得
若用 代替 ,则得到1阶近似公式,将式(10)代入可得广义Cook距离:
3.2.2. 似然距离
似然距离在一般情况下没有似然解,因此本文采用其一阶近似公式
把 换成 ,即可得似然距离的近似解
因此能得知,广义Cook距离与似然距离只多出了p。
4. 实例分析
下面用一个有关渔场捕鱼的数据来进行数值模拟分析,验证非线性模型在带有带右删失数据下的统计诊断具有可行性。
鱼卵数量与可捕获的成鱼数量之间的关系,是经营渔场者十分关心的问题。为研究二者之间的关系,Ricker和Smith(1975)给出了在Skeener河中红鳟鲑鱼的产卵量和可捕获的成鱼量的测量数据。表1 [9] 列出了这些数据;表中x为鱼卵量,y为可捕获成鱼的数量。所选用的模型为
,
考虑到y的前3个数据删失,假设 。数据如表1所示。
Table 1. Data of red trout salmon
表1. 红鳟鲑鱼数据
Continued
4.1. 参数估计
根据以上数据表,我们能解出参数 的估计值:
4.2. 影响分析
估计完参数之后,由数据删除模型计算得到广义Cook距离。图1是广义Cook距离的散点图。
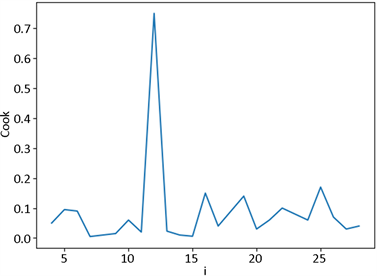
Figure 1. Scatter plot of generalized Cook distance
图1. 广义Cook距离的散点图
从图1可以看出:第12号点异于其他点,而且不涉及删失部分,因此第12号点为异常点。
5. 结束语
本文介绍了非线性模型在带有右删失数据下如何进行统计诊断的问题,给出了参数估计的方法以及如何通过统计诊断量判断强影响点或异常点,都是很经典很实际的办法;最后通过数值模拟分析,验证了诊断方法可行性。考虑到经典方法的局限性,本模型还可以用经验似然或其他方法进行更深一步的研究,这也是本文作者努力的方向。
基金项目
国家自然科学基金资助项目(11271189)。
文章引用
程 忠,冯 予. 非线性模型在右删失数据下的统计诊断
Statistical Diagnostics for Nonlinear Models with Right-Censored Data[J]. 统计学与应用, 2018, 07(06): 614-621. https://doi.org/10.12677/SA.2018.76070
参考文献
- 1. 韦博成, 鲁国斌, 等. 统计诊断引论[M]. 南京: 东南大学出版社, 1991.
- 2. 翟爽. 基于数据删除的广义线性模型诊断方法[D]: [硕士学位论文]. 哈尔滨: 东北林业大学理学院, 2012.
- 3. 胡宏昌, 崔恒建, 秦永松, 等. 近代线性回归分析方法[M]. 北京: 科学出版社, 2013.
- 4. 周勇. 广义估计方程估计方法[M]. 北京: 科学出版社, 2013.
- 5. 陈家鼎. 生存分析与可靠性[M]. 北京: 北京大学出版社, 2005.
- 6. 王思洋, 胡涛, 崔恒建. 删失数据非线性回归模型的广义M估计[J]. 北京师范大学学报(自然科学版), 2014, 50(1): 1-6.
- 7. 朱成莲. 带右删失数据的非线性模型的参数估计[J]. 统计与决策, 2009(14): 155-156.
- 8. 季文奇, 冯予. 右删失数据下广义线性模型的统计诊断[J]. 重庆理工大学学报(自然科学), 2017, 31(8): 174-181.
- 9. 韦博成, 林金官, 解锋昌. 统计诊断[M]. 北京: 高等教育出版社, 2009.
