Statistics and Application
Vol.
08
No.
04
(
2019
), Article ID:
31656
,
9
pages
10.12677/SA.2019.84070
“Photo Money” Task Pricing Research Based on Shenzhen-Guangzhou
Zhe Cui, Lifu Hu, Hao Li*
School of Automation, Shenyang Aerospace University, Shenyang Liaoning

Received: Jul. 19th, 2019; accepted: Aug. 1st, 2019; published: Aug. 12th, 2019

ABSTRACT
This paper discusses in depth the pricing problem of new self-service crowdsourcing platform software such as “taking photos to make money”. Using the idea of mathematical modeling to study its geographical location, membership density and task pricing, the main factors affecting the pricing law are obtained. On this basis, the tasks of different heat and price are packaged together, and a set of pricing scheme is established through linear regression, cluster analysis and other methods. The final result shows that the scheme is suitable for application, the price is reasonable, and has the advantages of practicality, high accuracy, strong attraction and mutual benefit.
Keywords:Principal Component Analysis, Membership Density, Packaging Condition Model, Analytic Hierarchy Process
基以深广为例的“拍照赚钱”任务 定价研究
崔哲,胡立夫,李浩*
沈阳航空航天大学自动化学院,辽宁 沈阳

收稿日期:2019年7月19日;录用日期:2019年8月1日;发布日期:2019年8月12日

摘 要
本文针对“拍照赚钱”这类新型自助式劳务众包平台软件的定价问题展开深入讨论。利用数学建模的思想对其地理位置,会员密度和任务定价进行研究,得到了影响定价规律的主要因素。在此基础上,将不同热度、价格的任务打包起来,通过线性回归、聚类分析等方法建立了一套定价方案。最终结果表明,建立的方案适合应用、价格合理,并且具有切合实际、准确度高、吸引力强、互惠共利等优点。
关键词 :主成分分析法,会员密度,打包条件模型,层次分析法

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着现代社会科技的迅捷发展,网络已经成为了人们生活中必不可少的一部分。许多APP已经悄然无声地走进了很多人的生活中,“拍照赚钱”正是众多新兴APP中的一员。人们可以使用APP在网上领取合适任务,比如去某超市拍摄某商品的上架情况,完成任务可以得到相应的奖励。对于这类APP,任务定价是核心因素,如果定价不合理,有的任务就会无人问津,而导致商品检查的失败。因此研究各个任务的定价规律,分析任务未完成的原因,从中吸取经验与教训对于“拍照赚钱”APP的运营是非常重要。
本文对所统计的深广各项数据进行分析,寻找出原有定价规律,找到部分任务未完成的原因。再结合影响价格的各种因素,通过优化得出一套新的定价规律。对于部分任务比较集中的情况,制定一种将任务打包到一起的标准。最后将根据得到的模型,为将要交付出的任务制定一个合理的赏金。
2. 基于线性回归未完成任务分析
2.1. 任务空间分布分析
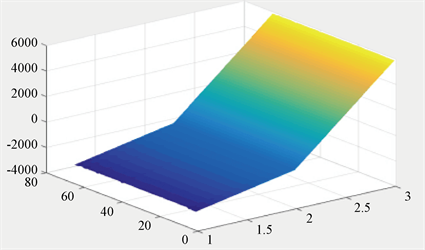
影响定价的因素是地理位置和完成度。如果是地理位置影响了定价,那么价格必然与距离有关。由于地球是一个球体,故而把经纬度转化为X、Y、Z三个直角坐标,并画出不用价格区间的空间分布,如图1。
由图1可以看出,两种任务的空间分布及其相似,都如带状分布,但定价为75的任务分布带更宽一些。
之后做出定价为65和75的任务经纬度分布散点图,同样可以发现所有任务都均匀分布在某一曲线的两侧。且定价越高的任务距离中心点的距离越远。为方便模型的使用,我们先选取最简洁的线性回归
的方式。通过MATLAB求解出完成度在不同经纬度下的分布直线方程为:
(1)
其中,E为经度,N为纬度。
 (a)
(a) (b)
(b)
Figure 1. Mission space distribution priced at 65(a) and 75(b)
图1. 定价为65(a)、75(b)的任务空间分布
对回归直线方程的拟合程度进行分析,结果如图2:

Figure 2. Residual distribution
图2. 残差分布
残差的P-P图将残差分布与正态分布相比较,对角线代表正态分布,残差的观测累计概率越靠近此线,则残差分布越接近正态分布 [1] 。
综合图2可知曲线拟合程度较好。
应用MATLAB求得各个任务点到中心曲线的距离 。由此得到距离的最大值和最小值为:
通过调查数据得到定价的最大值和最小值为:
默认价格按距离成线性增长,即得到方程:
代入 得到定价方案为:
所收集数据所在的位置大致在珠三角地区。通过地图,我们找到了一条连同广州和深圳的深广高速,如图3所示:
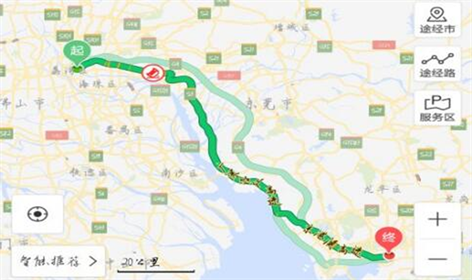
Figure 3. High speed image of Shenzhen and Guangzhou
图3. 深广高速图像
由图3可以看出,广深高速大致的地理位置和我们拟合出的中心曲线吻合 [2] 。
对于完成度的问题,我们进一步通过GPS和谷歌地图确定了各个任务点的实际位置绘制了图像,如图4:

Figure 4. GPS map
图4. GPS地图
对于完成度,本文同样作出了不同经纬度情况下的完成度情况的图像,如图5:
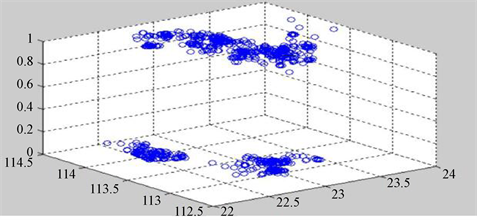
Figure 5. Distribution of completion degree in different longitude and latitude
图5. 完成度在不同经纬度下的分布
由图5不难看出,未完成的任务大多数集中在两端,而完成的任务则相对分布均匀。故本文猜测,完成度应该与地域的经济文化背景有关,而原来的定价标准未考虑此因素,导致了部分地区的完成度偏低 [3] 。
由上述内容不难发现:
1) 无论是完成度为1还是完成度为0的任务,其定价都与完成度没有明显的关联。这也从侧面验证了我们什么对于“定价仅与地理位置有关”的猜想是正确的。
2) 完成度为1的任务点相对集中在中间区域,而完成度为0的区域相对集中在两端。因此我们猜想完成度与地理位置有一定的关联。同时也说明了原先的定价方案对于地域因素考虑的还不够全面。
3) 广州和深圳地区的任务完成度整体较低,而东莞、佛山等地的任务完成度较高。所以可能是在定价的时候忽略了不同地区的经济情况,从而导致定价不合理,部分任务完成度偏低 [4] 。
2.2. 任务价格的修缮
由上述模型,可以发现定价与任务点的位置有关。但从任务完成度来看,这样的分配方式显然不合理。从的一些文献资料里了解到,定价应当与会员的分布密度有关联。一般而言,会员密度比较高的地区,任务比较受欢迎,任务价格应当低一些,而会员密度低的地方,为了提高任务的吸引力,应当把价格定高一些。实际绘制的任务分布图和会员分布图如图6:满足上述分析,一线城市会员分布多,且会员或者任务点集中的地区,任务完成度也比较低。

Figure 6. Membership profile
图6. 会员分布图
由此得出结论,会员密度大的地区定价应当提高,任务相对集中的地区定价应当降低。这与正常认知的会员密集度越高,完成度越高刚好相反。考虑到会员信誉度对完成情况的影响,对会员进行筛选。除去低于信誉度平均值的会员,再次作出高信誉度会员分布的散点图,分析图表可知,信誉度高的会员所在地区,恰好是任务完成度低的地区。这再一次证实了完成度与会员分布之间的反常规律 [5] [6] 。
2.3. 价格制定的完善
价格由地理位置(距离)和分布情况两者确定。分布情况则需要分别考虑会员的分布和任务点的分布。
通过编程计算出两组最短距离数据。由于无论是未完成的任务还是完成的任务,都是集群分布的,因此可以忽略任务的分布密度对定价的影响。对于会员密度,由于上文分析得到会员密度高的地方完成度都比较低,因此为了提高任务的完成度,必须提高这些地区的任务价格,增大任务吸引力。从最简单的定价与会员分布密度成线性关系讨论 [7] 。
由此得到如下函数关系:
(4)
通过计算和统计的数据可以知道:
代入公式(4)中,可以得到模型为:
(5)
之前求解出的模型为:
(3)
综合的定价m由p, q共同决定,我们先将其表示为
让 从0.1~0.9依次取值,计算出定价。
确立的新定价方案就是为了提高任务完成度,因此对于完成度低的任务,应该提高任务价格,增大任务吸引力,而对于完成度高的任务,可以适当降低任务价格,这样可以更好的提高任务完成度。因此在新的定价标准评价时,统计出完成度为0的时候差值为正的点的个数与完成度为1的时候差值为负的个数ni,再求出ni与所有任务数量的比值ωi [8] ,具体如表1:
Table 1. λ characteristic value table
表1. λ特征表
由表可以知,当λ = 0.2的时候,对于完成度的提高效果最好。因此我们的模型可以给出为:
(6)
3. 打包任务后价格的模型
3.1. 打包标准
由于部分任务比较集中,用户争抢,为了提高任务完成效率、减少多人争抢同一任务。决定将相近任务进行打包,并适度提高任务价格,更好地刺激会员参与到任务中来。打包应该满足以下两点:
1) 两打包点之间的距离短。(绝对距离短)
2) 打包点之间的距离比到用户之间的距离短 [9] 。(相对距离短)
3.1.1. 打包点的确立
根据前面的问题分析我们知道打包点应该满足的两个条件,下面就定量的研究打包条件。
针对第一个绝对距离小的条件,应该先求出所有任务点间的最短距离的几个特征数:期望(均值),众数,中位数。由于各个任务点间的最短距离大多数是不同的,因此我们研究众数没有意义。而对于期望和中位数问题。
计算出期望 和中位数
由结果可以看出,期望和中位数之间的差距比较大。因此两者之间必然有一个数据是不合理的。绘制出任务点的散点图如图7:

Figure 7. Task point distribution
图7. 任务点分布图
由散点图可以看出,有部分的任务是单独分散开的,它到所有任务点的距离都比较远,这些点把距离的期望拉高了,所以期望值已经不能合理的反应任务点分布的一般规律了。但是中位数并不受这些分散的任务点的影响。因此将中位数作为确立打包点的第一个标准。即
针对第二个标准,要求打包点之间的距离比到用户之间的距离短。最直观的做法就是吧两个距离作比值进行比较。考虑到研究时是针对两个任务点而言的。将两个任务点分别标记为A1,A2,将会员位置标记为B。那么根据要求就有如下不等式:
要同时满足这个条件就必须满足 。
其大致图解如图8:

Figure 8. Model diagram
图8. 模型图解
也就说如果 ,就将这两个点打包成一个任务发布。
综合这些分析得到打包标准为: 。
经过筛选之后满足条件的点只有六个 [10] 。
3.1.2. 关于打包后任务的定价方案
对于打包任务,其目的就是为了提高任务吸引力,提高冷门任务完成率、刺激会员完成任务。因此,对于打包好的任务,应该在原任务的基础上适度提高价格。但考虑到实际背景,打包后提高的价格必须在一定的限度内。如果提高的太多,相对而言,单个任务的吸引力就会降低。因此我们的提价在一定的范围内小幅度提升。由以上的各种因素影响,确立一个新的定价标准:取两者到中心直线的距离最大值为打包后到中心直线的距离,取两点间会员密度最大值为打包后会员密度,这样提高了打包后任务的定价,可以提高任务完成度。
通过前面的筛选,得到了六个三对可以打包的点,最终得到这六个点的打包后的最优价格 [11] ,如表2:
Table 2. Packing price list
表2. 打包后价格表
4. 结语
本文建立了一种基于层次分析法,主成分分析的APP价格制定,任务打包模型。在实际价格上进行分析推算,得出的更合理的价格制定方案。通过层次分析法对模型中涉及的众多影响因素进行量化和定性分析,令模型更具说服性。本模型的特点包括:
1) 模型打包之后,任务可以更快地交付给会员们,有效提高了任务完成效率,也可以提高会员的积极性。
2) 主成分分析法是通过考虑多个因素来寻找对某一种变量的影响,具有很好的应用性,在众多相似问题中都可以用这类打包方法,比如快递跑腿,外卖配送软件、图像处理等方面。
3) 结合了SPSS,CODEBLOCKS,MAT LAB等软件,灵活地运用主成分分析法,曲线拟合等方法,使结论更加精确。
除此之外,本文所建立的基于多种数学算法的模型能够结合实际情况来解决定价问题,具有很好的通用性和推广性,所以在投资理财等相似问题中我们也都可以应用该方法。
基金项目
沈阳航空航天大学大学生创新创业训练项目(项目编号110418346)。
文章引用
崔 哲,胡立夫,李 浩. 基以深广为例的“拍照赚钱”任务定价研究
“Photo Money” Task Pricing Research Based on Shenzhen-Guangzhou[J]. 统计学与应用, 2019, 08(04): 613-621. https://doi.org/10.12677/SA.2019.84070
参考文献
- 1. 陈崇双, 唐家银, 何平. 方差分析法的线性回归建模重构[J]. 统计与决策, 2018, 34(7): 71-75.
- 2. 徐雅静, 汪远征, 等. 主成分分析应用方法的改进[J]. 数学的实践与认识, 2006, 36(6): 68-75.
- 3. 孙婷蔚. 统计回归模型中的主成分分析[J]. 通讯世界, 2019, 26(3): 169-170.
- 4. 郭呈全, 陈希镇. 主成分回归的SPSS实现[J]. 统计与决策, 2011(5): 157-159.
- 5. 金蛟. 主成分分析方法在综合评价中的应用[J]. 中国卫生统计, 2008, 25(1): 72+74.
- 6. 贾月恬, 钟妍, 梁定康. 打包机制下的任务定价模型[J]. 中国集体经济, 2018(7): 77-78.
- 7. 王正光. 论数学建模与数学模型[J]. 纳税, 2018(19): 237-238+242.
- 8. 陈璇, 游小宝, 郑崇伟, 孙威, 谢胜浪. 一种新的线性回归模型及其应用示例[J]. 大气科学, 2019, 43(2): 389-400.
- 9. 杜家菊, 陈志伟. 使用SPSS线性回归实现通径分析的方法[J]. 生物学通报, 2010, 45(2): 4-6.
- 10. 冷建飞, 高旭, 朱嘉平. 多元线性回归统计预测模型的应用[J]. 统计与决策, 2016(7): 82-85.
- 11. Liu, Z. (2012) Based on the Mathematical Modeling Thought Method Exploration. Advanced Materials Research, 450-451, 646-649. https://doi.org/10.4028/www.scientific.net/AMR.450-451.646
NOTES
*通讯作者。
