Advances in Applied Mathematics
Vol.3 No.04(2014), Article
ID:14302,7
pages
DOI:10.12677/AAM.2014.34027
Acceptance Sampling Plans with Type-I Hybrid Censoring Scheme of Weibull Distribution
School of Mathematics and Computational Science, Sun Yat-Sen University, Guangzhou
Email: sysuljw@126.com
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Aug. 15th, 2014; revised: Sep. 25th, 2014; accepted: Oct. 4th, 2014
ABSTRACT
Lifetime is an important quality variable of a product. Sampling plans used to determine the acceptability of a product, with respect to its lifetime, are known as acceptance sampling plans. In this paper, we discuss acceptance sampling plans of Weibull distribution with considering the Type-I hybrid censoring schemes. Firstly, we give the exact conditional distribution of the maximum likelihood estimator (MLE) of the scale parameter. Secondly, using the exact distribution of a pivotal quantity, we establish an acceptance sampling procedure satisfying the producer and consumer risks. Finally, some numerical results are tabulated for illustration.
Keywords:MLE, Type-I Hybrid Censoring, Consumer Risk, Producer Risk

基于混合I型删失数据威布尔模型的
可接受抽样计划
李嘉伟
中山大学,数学与计算科学学院,广州
Email: sysuljw@126.com
收稿日期:2014年8月15日;修回日期:2014年9月25日;录用日期:2014年10月4日

摘 要
寿命是产品质量的一个重要指标。根据产品的寿命指标,用于确定产品的接受程度的可靠性试验,被称为可接受抽样计划。本文研究了基于混合I型删失数据的威布尔模型可接受抽样计划。首先,我们给出了威布尔分布尺度参数最大似然估计的精确分布。进而根据枢轴量的精确分布,在消费者与生产者风险可控的条件下,我们给出了可接受抽样计划的执行方法。最后为了展示本文的方法,我们给出了一些可接受抽样计划的数值模拟结果。
关键词
最大似然估计,混合I型删失,消费者风险,生产者风险

1. 引言
在可靠性研究中,威布尔模型被广泛的应用与寿命数据分析。在众多的删失试验计划中,混合-I型删失计划是比较常见的一种。假设有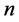 个相同的试验样品投入相同试验环境的寿命试验,并且它们它们的寿命是独立同分布的随机变量。寿命试验选择在一个指定的看到
个相同的试验样品投入相同试验环境的寿命试验,并且它们它们的寿命是独立同分布的随机变量。寿命试验选择在一个指定的看到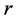 个失效得试验个体时或是在某一个指定的实效时刻
个失效得试验个体时或是在某一个指定的实效时刻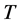 时终止,即终止时刻为:
时终止,即终止时刻为: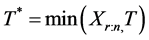 ,这里的r和T由试验人员在试验之前预先设定。因此在这种删失计划下,试验者可以得到以下两种类型的观测数据。第一种:当
,这里的r和T由试验人员在试验之前预先设定。因此在这种删失计划下,试验者可以得到以下两种类型的观测数据。第一种:当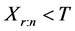 时,试验者看到如下数据:
时,试验者看到如下数据: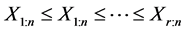 ,
,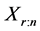 表示第r个失效寿命数据。第二种:当
表示第r个失效寿命数据。第二种:当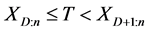 而且
而且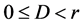 时,试验者看到如下数据:
时,试验者看到如下数据: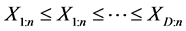 ,这里的
,这里的 表示在
表示在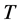 之前观测到的失效个体数目。
之前观测到的失效个体数目。
Epstein [1] 首先提出这一删失计划,并且研究了指数分布失效率的置信区间。Fairbanks等[2] 改进了Epstein的相关结论。Chen和Bhattacharya [3] 获得了指数分布参数MLE的精确分布函数以及在混合删失条件下参数的置信区间。在Chen和Bhattacharya的研究基础上,Gupta和Kundu [4] 获得了参数的精确置信区间。在混合-I型和混合-II型情形下,Childs等[5] 得到了参数MLE精确分布更为简洁的表达形式。上述文献的研究结果都是基于指数分布参数MLE的分布函数是单调递增函数得到的,相关证明都只是通过数值模拟加以验证。随后,Balakrishnan和Iliopoulos [6] 对于这一假设给出了严格的证明。
可接受抽样计划是删失数据条件下寿命试验的一个重要研究问题。一个可接受抽样计划包含寿命试验规则以及基于这些规则,在试验数据条件下,试验者必须决定是接受试验结果还是拒绝接受相关结果。完整的寿命测试计划(LTP)是在生产者风险和消费者风险都必须可控的条件下进行。大量的文献对此进行了研究,Epstein考虑了在指数情形下的试验设计问题。Jeong等[7] 研究了混合抽样计划指数分布的抽样问题。Fertig和Mann [8] 考虑了混合计划下威布尔分布的LTP问题。Chen等[9] 等利用贝叶斯方法讨论了混合计划下威布尔分布的LTP问题。Kim和Yum [10] 讨论了了加速寿命试验下的混合删失去威布尔分布的LTP问题。利用似然比方法,Tsai和Lin [11] 提出了在循序区间删失计划下的LTP问题。更大LTP问题的研究文献可参考:Tse和Yang [12] ,Ng等[13] ,Balasooriya和Low等[14] 以及Tsai和Wu [15] 。本文中,我们首先得到了威布尔分布尺度参数MLE的精确分布。利用精确分布函数,我们在文章中构造了一个枢轴量。进而在消费者与生产者风险都可控的条件下,我们设计了一个可接受抽样计划试验步骤。
2. 尺度参数的精确分布
一个随机变量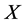 被称为服从威布尔分布,若其概率密度函数(pdf)和分布函数(cdf)分别为:
被称为服从威布尔分布,若其概率密度函数(pdf)和分布函数(cdf)分别为:
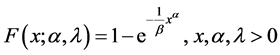
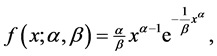 。
。
这里的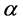 和
和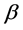 分别是形状参数和尺度参数。一个具有形状参数
分别是形状参数和尺度参数。一个具有形状参数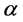 和尺度参数
和尺度参数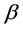 的威布尔分布一般简记为:
的威布尔分布一般简记为: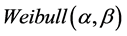 。在混合-I型删失计划下,寿命试验在一个随机时刻
。在混合-I型删失计划下,寿命试验在一个随机时刻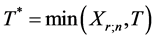 处终止,这里的
处终止,这里的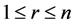 及
及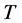 预先给定。我们记在
预先给定。我们记在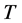 之前观测到的失效个体数是
之前观测到的失效个体数是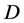 ,显然
,显然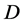 是一个具有如下分布律的离散型随机变量:
是一个具有如下分布律的离散型随机变量:
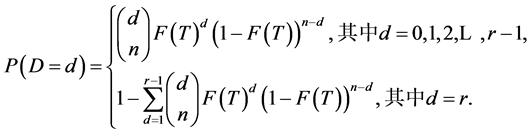
为了获得参数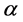 和
和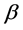 的MLE以及精确分布函数,我们必须假定是
的MLE以及精确分布函数,我们必须假定是 。以下分不同观测数据类型讨论。
。以下分不同观测数据类型讨论。
情形1:当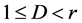 和
和 时,我们可以得到观测数据:
时,我们可以得到观测数据: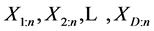 。基于这些观测数据的似然函数为:
。基于这些观测数据的似然函数为:
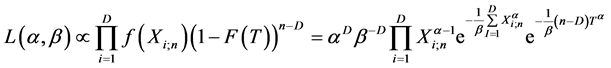
情形2:当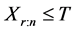 时,我们可以得到观测数据:
时,我们可以得到观测数据: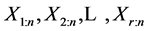 。基于这些观测数据的似然函数为:
。基于这些观测数据的似然函数为:
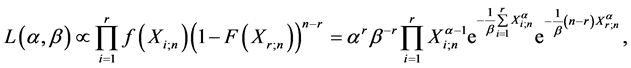
使用一个简单的迭代数值算法,我们可以得到参数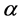 和
和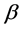 的近似MLE,分别记为
的近似MLE,分别记为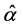 和
和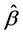 。且有
。且有
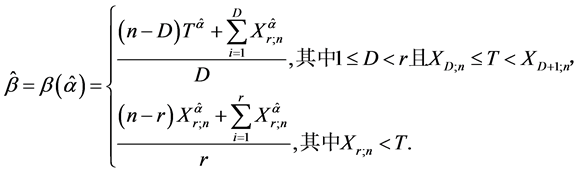 (1)
(1)
这里的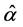 是以下(2)和(3)两个方程的解。
是以下(2)和(3)两个方程的解。
 (2)
(2)
 (3)
(3)
众所周知,如果随机变量X服从威布尔分布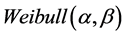 。则随机变量
。则随机变量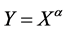 服从具有概率密度函
服从具有概率密度函
数函数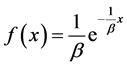 的指数分布
的指数分布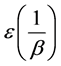 ,这里
,这里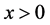 。为了获得尺度参数
。为了获得尺度参数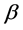 的精确分布,我们利用了威布
的精确分布,我们利用了威布
尔分布与指数分布的转换。在以后的推断中我们假定形状参数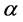 是已知的。因此我们可以获得两种不同的观测数据:
是已知的。因此我们可以获得两种不同的观测数据: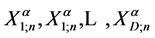 当
当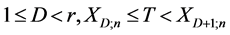 时及
时及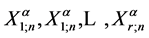 当
当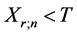 时。这些新数
时。这些新数
据服从具有失效率参数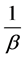 的指数分布,由于
的指数分布,由于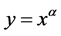 关于
关于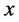 是单调递增函数,因此可以得到混合删失时刻
是单调递增函数,因此可以得到混合删失时刻
为: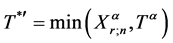 。利用Chen和Bhattacharyya [4] 的结论,基于这些转换数据,尺度参数
。利用Chen和Bhattacharyya [4] 的结论,基于这些转换数据,尺度参数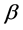 的MLE为
的MLE为
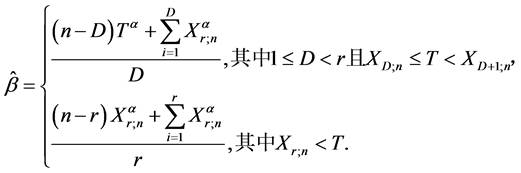 (4)
(4)
一个很有意思的结论是,我们看到利用转换数据得到的参数MLE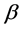 (1)式与直接利用威布尔分布数据得到的MLE
(1)式与直接利用威布尔分布数据得到的MLE (4)是完全相同的。从(4)式可以看到参数
(4)是完全相同的。从(4)式可以看到参数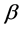 的MLE的精确表达式依赖于参数
的MLE的精确表达式依赖于参数 。由于转换
。由于转换
数据来自具有失效率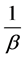 的指数总体,因此尺度参数
的指数总体,因此尺度参数 的MLE的精确分布可以得到。我们得到以下的定理。
的MLE的精确分布可以得到。我们得到以下的定理。
定理1:在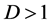 的条件下,
的条件下,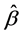 的pdf由下式给出
的pdf由下式给出
*

其中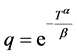
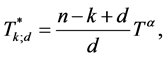
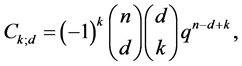 ,
, 是通常的gamma分布的概率密度函数。
是通常的gamma分布的概率密度函数。
证明:这里的证明与Childs等[6] 相似,可以参考相关细节,此处略。
定理2:在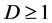 的条件下,
的条件下,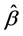 的生存函数由下式给出
的生存函数由下式给出
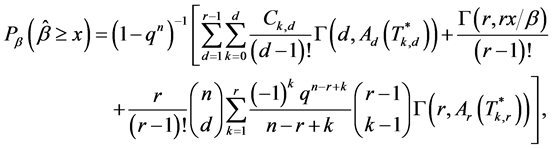
这里的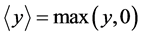
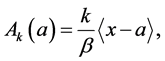 及
及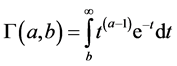 是不完全gamma函数。
是不完全gamma函数。
证明:由定理1的概率密度函数直接积分,便可以获得结论,此处略。
在混合-I型删失条件下,利用随机序关系,Balakrishnan和Iliopoulos [7] 证明了指数分布期望寿命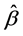 的MLE是关于参数
的MLE是关于参数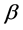 是随机递增函数。利用这一随机单调性,我们可以设计满足生产者风险与消费者风险都可控的可接受抽样计划。
是随机递增函数。利用这一随机单调性,我们可以设计满足生产者风险与消费者风险都可控的可接受抽样计划。
3. 可接受抽样计划
在这一部分,我们主要讨论基于试验样品的可接受抽样计划。利用参数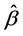 的精确分布,我们可以找到试验需要的样品数目。
的精确分布,我们可以找到试验需要的样品数目。
3.1. 可接受抽样计划步骤
一个众所周知的结果是服从威布尔分布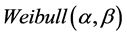 的试验样品的平均寿命时间是
的试验样品的平均寿命时间是
 ,这里的
,这里的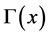 是通常的Gammm函数。为了设计可接受抽样计划步骤,假定形状参数
是通常的Gammm函数。为了设计可接受抽样计划步骤,假定形状参数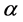
是已知的。试验的决策原则是:在混合-I型删失情形下,如果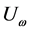 大于等于
大于等于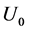 ,我们就接受这一批试验样品;反之,我们就拒绝这批试验样品,如果
,我们就接受这一批试验样品;反之,我们就拒绝这批试验样品,如果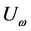 小于
小于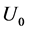 ,这里的参数
,这里的参数 是两个有试验人员设定的常数。这样导致这一试验问题等价于假设检验:
是两个有试验人员设定的常数。这样导致这一试验问题等价于假设检验:
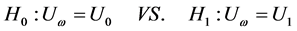
或是等价检验
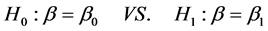
其中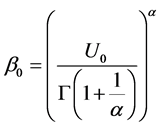 ,
,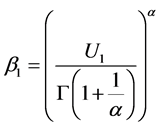 。
。
从(7)式可知,参数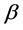 的MLE为:
的MLE为:

假定C是一个正实数,生产者的风险(PR)是在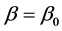 条件下,这些试验样品被拒绝的概率。消费的风险(CR)是在
条件下,这些试验样品被拒绝的概率。消费的风险(CR)是在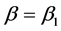 条件下,这些试验样品被接受的概率。这两种风险由下式给出:
条件下,这些试验样品被接受的概率。这两种风险由下式给出:
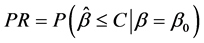
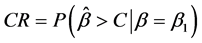
则试验设计参数LTP(n,C)是试验样品数目n以及试验判断的临界值C构成。它们的取值,可有以下两个方程决定。
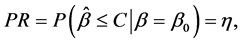 (5)
(5)
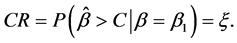 (6)
(6)
这里的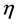 和
和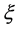 分别是事先指定的生产者风险参数和消费者风险参数。由于样本容量参数是整数,上诉方程可能无法得到满足条件(5)式和(6)式的整数解(n,C)。因此最小满足风险可控的n和C由以下两个不等式决定:
分别是事先指定的生产者风险参数和消费者风险参数。由于样本容量参数是整数,上诉方程可能无法得到满足条件(5)式和(6)式的整数解(n,C)。因此最小满足风险可控的n和C由以下两个不等式决定:
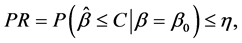
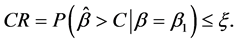
或是等价于以下不等式
 (7)
(7)
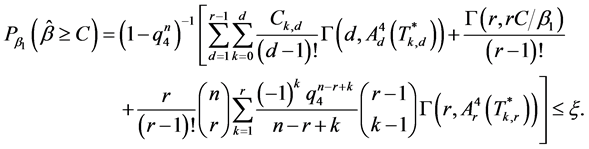 (8)
(8)
这里的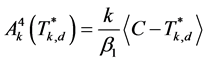
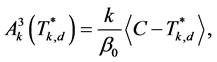
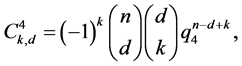

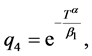
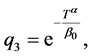 。
。
这个选择最小的试验参数满足(7)式和(8)式n和C的具体算法是:
第一步:指定参数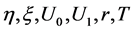 和
和
第二步:令 。
。
第三步:在满足(7式的条件下,选择满足条件的最大的C。如果(n,C)还同时满足(8)式,则最优的试验参数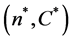 就找到了。否则进入第四步。
就找到了。否则进入第四步。
第四步:令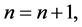 同时回到第三步。
同时回到第三步。
3.2. 数值试验
为了演绎本文的方法,我们给出了相关数值试验。假定试验样品的寿命服从威布尔分布 其中形状参数
其中形状参数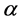 已知,尺度参数
已知,尺度参数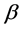 未知。当
未知。当 时,失效率函数关于t是递增函数,这一情况与真实的试验情形不太一致。在数值试验时,我们只讨论了参数
时,失效率函数关于t是递增函数,这一情况与真实的试验情形不太一致。在数值试验时,我们只讨论了参数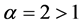 的情形。同时我们设计了试验参数
的情形。同时我们设计了试验参数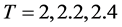
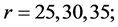 。令
。令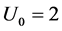 和
和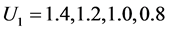 。设定生产者风险参数
。设定生产者风险参数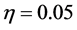 和
和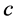 消费者风险参数
消费者风险参数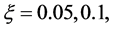 相关数值试验结果在表1中给出,从试验结果,我们可以得到以下结论:
相关数值试验结果在表1中给出,从试验结果,我们可以得到以下结论:
1) 当增大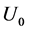 和
和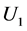 的差距时,需要的试验样品数目有递减的趋势。
的差距时,需要的试验样品数目有递减的趋势。
2) 当增大删失时刻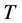 时,需要的试验样品数目有递减的趋势。
时,需要的试验样品数目有递减的趋势。
3) 一般说来,当增大观测的试验样品数目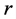 才终止试验时,需要的试验样品数目有递增的趋势。
才终止试验时,需要的试验样品数目有递增的趋势。
4) 在相同的生产者风险参数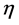 条件下,随着消费者风险参数
条件下,随着消费者风险参数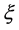 的增加,需要的试验样品数目有递减的趋势。
的增加,需要的试验样品数目有递减的趋势。
4. 结论
在本文中,我们讨论了基于混合-I型删失数据情形下的威布尔分布的统计推断问题。在生产者风险与消费者风险都可控的条件下,利用参数 的MLE的精确分布,我们设计了一个可接受抽样的试验步骤。对于不同的试验参数,我们给出了相关数值试验结果来演绎本文的方法。通过数值试验,我们看到在不同的试验参数条件下,试验所叙述为样品数目都是比较适中的,这表明这一方法是可行的。在不同的试验删失计划下,我们可以考虑将这一方法推广到寿命试验更为广泛的模型,比如gamma分布,Pareto分布,log-normal模型等等。这些推广的研究结果是值得期待和研究的。
的MLE的精确分布,我们设计了一个可接受抽样的试验步骤。对于不同的试验参数,我们给出了相关数值试验结果来演绎本文的方法。通过数值试验,我们看到在不同的试验参数条件下,试验所叙述为样品数目都是比较适中的,这表明这一方法是可行的。在不同的试验删失计划下,我们可以考虑将这一方法推广到寿命试验更为广泛的模型,比如gamma分布,Pareto分布,log-normal模型等等。这些推广的研究结果是值得期待和研究的。
表1. 可接受抽样计划模拟结果(α = 2)
参考文献 (References)
- [1] Epstein, B. (1954) Truncated life tests in the exponential case. Annals of the Institute of Statistical Mathematics, 25, 55-564.
- [2] Fairbanks, K., Madson, R. and Dykstra, R. (1982) A condence interval for an exponential parameter from a hybrid life test. Journal of the American Statistical Association, 77, 137-140.
- [3] Chen, S. and Bhattacharya, G.K. (1988) Exact condence bounds for an exponential parameter under hybrid censoring. Communications in Statistics—Theory and Methods, 17, 1857-1870.
- [4] Gupta, R.D. and Kundu, D. (1998) Hybrid censoring schemes with exponential failure distribution. Communications in Statistics—Theory and Methods, 27, 3065-3083.
- [5] Childs, A., Chandrasekhar, B., Balakrishnan, N. and Kundu, D. (2003) Exact likelihood inference based on type-I and type-II hybrid censored samples from the exponential distribution. Annals of the Institute of Statistical Mathematics, 55, 319-330.
- [6] Balakrishnan, N. and Iliopoulos, G. (2009) Stochastic monotonicity of the MLE of exponential mean under different censoring schemes. Annals of the Institute of Statistical Mathematics, 61, 753-772.
- [7] Jeong, H.S., Park, J.I. and Yum, B.J. (1996) Development of (r; T) hybrid sampling plans for exponential lifetime distributions. Journal of Applied Statistics, 23, 601-607.
- [8] Fertig, K.W. and Mann, N.R. (1980) Life test sampling plans for two-parameter Weibull populations. Technometrics, 22, 165-177.
- [9] Chen, J., Chou, W., Wu, H. and Zhou, H. (2004) Designing acceptance sampling schemes for life testing with mixed censoring. Naval Research Logistics, 51, 597-612.
- [10] Kim, M. and Yum, B.J. (2009) Life test sampling plans for Weibull distributed lifetimes under accelerated hybrid censoring. Statistical Papers, 52, 327-342.
- [11] Tsai, T.R. and Lin, C.W. (2008) Acceptance sampling plans under progressive interval censoring with likelihood ratio. Statistical Papers, 51, 259-271.
- [12] Tse, S.K. and Yang, C. (2003) Reliability sampling plans for the Weibull distribution under Type-II progressive censoring with binomial removals. Journal of Applied Statistics, 30, 709-718.
- [13] Ng, H.K.T., Chan, P.S. and Balakrishnan, N. (2004) Optimal progressive censoring plans for the Weibull distribution. Technometrics, 46, 470-481.
- [14] Balasooriya, U. and Low, C.K. (2004) Competing causes of failure and reliability tests for Weibull lifetimes under Type-I progressive censoring. IEEE Transactions on Reliability, 53, 29-36.
- [15] Tsai, T.R. and Wu, S.J. (2006) Acceptance sampling based on truncated life tests for generalized Rayleigh distribution. Journal of Applied Statistics, 33, 595-600.
