设为首页 加入收藏 期刊导航 网站地图

Advances in Applied Mathematics
Vol.07 No.08(2018), Article ID:26536,12 pages
10.12677/AAM.2018.78118

A Finite Difference Method for Unsteady Double-Diffusive Natural Convection in Porous Medium

Zhifei Cai

School of Mathematics and Physics, North China Electric Power University, Beijing

Received: Aug. 1st, 2018; accepted: Aug. 15th, 2018; published: Aug. 22nd, 2018

ABSTRACT

A finite difference method is used to numerically solve unsteady double-diffusive natural convection in porous medium. A staggered grid finite difference scheme is established, and the stability analysis and convergence order are provided. Finally, some numerical examples are presented to verify the feasibility and efficiency of the staggered grid finite difference scheme. The results are compared with previously published work and excellent agreement has been obtained.

Keywords:Unstable Double-Diffusive Natural Convection, Finite Difference Scheme, Stability and Error Estimates, Numerical Simulation

多孔介质中非平稳双扩散自然对流的 有限差分法

蔡志飞

华北电力大学，数理学院，北京

收稿日期：2018年8月1日；录用日期：2018年8月15日；发布日期：2018年8月22日

摘 要

本文用有限差分方法求多孔介质中非平稳双扩散自然对流问题的数值解，建立了交错网格有限差分格式，并给出这种格式的稳定性分析和收敛阶。最后，用数值算例验证该格式的可行性和有效性，模拟结果与以往发表的工作成果进行了比较，具有非常好的一致性。

关键词 :非平稳双扩散自然对流，交错网格，有限差分格式，误差分析

Copyright © 2018 by author and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

多孔介质中的传热传质普遍存在于工农业生产与日常生活领域中，如：地热过程，石油热采技术，核反应堆的设计，太阳能收集，过滤工艺及干燥工艺等。在腔体中，由于存在温度梯度和浓度梯度，产生浮力比，从而引起了自然对流，影响其传热传质性能 [1] [2] 。

这种双扩散导致的自然对流问题在许多工程应用中具有十分重要的作用。由于描述实际问题的流体力学问题的源函数或计算区域很复杂，要求算出其精确解往往不容易，有效可行的方法是求其数值解，交错网格的有限差分方法是求解流体力学方程的最有效方法之一。由于问题的复杂性，最初的研究工作只是就水平多孔层垂直方向上存在温度梯度和浓度梯度的情形进行探讨，主要研究流动的稳定性问题。近年来，由双扩散引起的自然对流传热传质的研究受到了研究者的广泛关注，已经能够对简单的几何情形进行研究。文献 [3] 对多孔梯形腔体底壁加热(均匀或非均匀)引起的自然对流进行了数值研究。文献 [4] 研究了方形腔中多孔介质在不同温差纵横比下的非达西浮力流动。文献 [5] 对三角形腔体中底壁加热(均匀或非均匀)而产生的自然对流进行了有限元模拟。文献 [6] 详细研究了自然对流换热中可变孔隙度模型的发展。最近，文献 [7] 采用有限体积元法研究了当边界均匀或非均匀加热时，浮力比和热瑞利数对双扩散自然对流的影响。

本文首先建立了非平稳双扩散自然对流问题的交错网格有限差分格式，其次对该有限差分格式进行了稳定性分析，并利用泰勒展开给出了该差分格式的收敛阶，最后数值模拟了各个时刻的流线、温度线和浓度线的分布状况。

2. 数学模型和有限差分格式

如图1所示，多孔介质封闭方形腔体中，充满流体。假设腔体上壁是绝热的，腔体下壁和左壁持续加热，右壁进行冷却保持恒温。由于存在温度梯度和浓度梯度而产生浮力比，从而产生自然对流传热传质。

Figure 1. System chart

图1. 系统简图

引入Boussinesq假设及Darcy定律，并引进无量纲变量，考虑如下双扩散自然对流方程 [8] ：

∂ u ∂ x + ∂ v ∂ y = 0   , (1)

∂ u ∂ t = − ∂ p ∂ x + P r ( ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 ) − 1 ε ( ∂ u 2 ∂ x + ∂ u v ∂ y 2 ) − P r D a u − 1.75 u 2 + v 2 150 D a ε u   , (2)

∂ u ∂ t = − ∂ p ∂ y + P r ( ∂ 2 v ∂ x 2 + ∂ 2 v ∂ y 2 ) − 1 ε ( ∂ v 2 ∂ y + ∂ u v ∂ x ) − P r D a v − 1.75 u 2 + v 2 150 D a ε v + P r R a ( θ + M S ) , (3)

∂ θ ∂ t = ( ∂ 2 θ ∂ x 2 + ∂ 2 θ ∂ y 2 ) − ( ∂ u θ ∂ x + ∂ v θ ∂ y ) , (4)

∂ S ∂ t = 1 L e ( ∂ 2 S ∂ x 2 + ∂ 2 S ∂ y 2 ) − ( ∂ u S ∂ x + ∂ v S ∂ y ) . (5)

这里x和y分别是水平方向和垂直方向上的无量纲坐标，u，v分别是x，y方向上的速度分量， θ 和S分别表示无量纲温度和浓度；p是无量纲压力参数。另外， P r   , ε , D a   , R a , M   , L e 分别是普朗特数，多孔介质的孔隙度，达西数，雷利数，浮力比和刘易斯数，它们将对流动，换热和传质产生重要影响。

初始条件：当t = 0时，对于 0 ≤ x , y ≤ 1

u ( x , y ) = 0 = v ( x , y ) , θ ( x , y ) = 0 , S ( x , y ) = 0. (6)

边界条件：当t > 0时

u ( x , 1 ) = u ( x , 0 ) = u ( 0 , y ) = u ( 1 , y ) = 0 , (7)

v ( x , 0 ) = v ( x , 1 ) = v ( 0 , y ) = v ( 1 , y ) = 0 , (8)

θ ( x , 0 ) = 1 , ∂ θ ∂ y ( x , 1 ) = 0 , (9)

θ ( 0 , y ) = 1 , θ ( 1 , y ) = 0 , (10)

S ( x , 0 ) = 1 , ∂ S ∂ y ( x , 1 ) = 0 , (11)

S ( 0 , y ) = 1 ,           S ( 1 , y ) = 0. (12)

设 Δ x , Δ y 分别是x方向和y方向的空间步长， Δ t 表示时间步长， N = [ T / Δ t ] ，通过在点 ( x i , y k , t n ) 处离散 θ , p , S ，在点 ( x j + 1 2 , y k , t n ) 处离散u，在点 ( x j , y k + 1 2 , t n ) 处离散v，可以得到下列交错网格有限差分格式：

u j + 1 2 , k n + 1 − u j − 1 2 , k n + 1 Δ x + v j , k + 1 2 n + 1 − v j , k − 1 2 n + 1 Δ y = 0 (13)

u j + 1 2 , k n + 1 − u j + 1 2 , k n Δ t = − p j + 1 , k n − p j , k n Δ x + P r ( u j + 3 2 , k n − 2 u j + 1 2 , k n + u j − 1 2 , k n Δ x 2 + u j + 1 2 , k + 1 n − 2 u j + 1 2 , k n + u j + 1 2 , k − 1 n Δ y 2 )     − 1 ε ( ( u 2 ) j + 1 , k n − ( u 2 ) j , k n Δ x + ( u v ) j + 1 2 , k + 1 2 n − ( u v ) j + 1 2 , k − 1 2 n Δ y )     − P r ε D a u j + 1 2 , k n − 1.75 u j + 1 2 , k n ( u 2 ) j + 1 2 , k n + ( v 2 ) j + 1 2 , k n 150 D a ε (14)

v j , k + 1 2 n + 1 − v j , k + 1 2 n Δ t = − p j , k + 1 n − p j , k n Δ y + P r ( v j + 1 , k + 1 2 n − 2 v j , k + 1 2 n + v j − 1 , k + 1 2 n Δ x 2 + v j , k + 3 2 n − 2 v j , k + 1 2 n + v j , k − 1 2 n Δ y 2 )     − 1 ε ( ( v 2 ) j , k + 1 n − ( v 2 ) j , k n Δ y + ( u v ) j + 1 2 , k + 1 2 n − ( u v ) j − 1 2 , k + 1 2 n Δ x ) − P r ε D a v j , k + 1 2 n     − 1.75 v j , k + 1 2 n ( u 2 ) j + 1 2 , k n + ( v 2 ) j , k + 1 2 n 150 D a ε + P r R a ( θ j , k + 1 2 n + N S j , k + 1 2 n ) (15)

θ j , k n + 1 − θ j , k n Δ t = ( θ j + 1 , k n − 2 θ j , k n + θ j − 1 , k n Δ x 2 + θ j , k + 1 n − 2 θ j , k n + θ j , k − 1 n Δ y 2 )     − ( ( u θ ) j + 1 2 , k n − ( u θ ) j − 1 2 , k + 1 2 n Δ x + ( v θ ) j , k + 1 2 n − ( v θ ) j , k − 1 2 n Δ y ) (16)

S j , k n + 1 − S j , k n Δ t = 1 L e ( S j + 1 , k n − 2 S j , k n + S j − 1 , k n Δ x 2 + S j , k + 1 n − 2 S j , k n + S j , k − 1 n Δ y 2 )     − ( ( u S ) j + 1 2 , k n − ( u S ) j − 1 2 , k n Δ x + ( v S ) j , k + 1 2 n − ( v S ) j , k − 1 2 n Δ y ) (17)

将(14)式和(15)式代入(13)式得到关于p的泊松方程：

p j + 1 , k n − 2 p j , k n + p j − 1 , k n Δ x 2 + p j , k + 1 n − 2 p j , k n + p j , k − 1 n Δ y 2 = R 2     ( n = 0 , 1 , ⋯ , N ) (18)

R n = ( u ˜ j + 1 2 , k n − u ˜ j − 1 2 , k n ) + ( v ˜ j , k + 1 2 n − v ˜ j , k − 1 2 n )

其中， u ˜ j + 1 2 , k n = u j + 1 2 , k n Δ x Δ t + P r ( u j + 3 2 , k n − 2 u j + 1 2 , k n + u j - 1 2 , k n Δ x 3 + u j + 1 2 , k + 1 n − 2 u j + 1 2 , k n + u j + 1 2 , k - 1 n Δ x Δ y 2 )     − 1 ε ( ( u 2 ) j + 1 , k n − ( u 2 ) j , k n Δ x 2 + ( u v ) j + 1 2 , k + 1 2 n − ( u v ) j + 1 2 , k − 1 2 n Δ x Δ y ) − P r ε Δ x D a u j + 1 2 , k n     − 1.75 u j + 1 2 , k n ( u 2 ) j + 1 2 , k n + ( v 2 ) j + 1 2 , k n Δ x 150 D a ε

v ˜ j , k + 1 2 n = u j , k + 1 2 n Δ y Δ t + P r ( v j + 1 , k + 1 2 n − 2 v j , k + 1 2 n + u j -1 , k + 1 2 n Δ x 2 Δ y + v j , k + 3 2 n − 2 v j , k + 1 2 n + v j , k - 1 2 n Δ y 3 )     − 1 ε ( ( v 2 ) j , k + 1 n − ( u 2 ) j , k n Δ y 2 + ( u v ) j + 1 2 , k + 1 2 n − ( u v ) j − 1 2 , k + 1 2 n Δ x Δ y ) − P r ε Δ y D a v j , k + 1 2 n     − 1.75 v j , k + 1 2 n ( u 2 ) j , k + 1 2 n + ( v 2 ) j , k + 1 2 n Δ y 150 D a ε + P r R a Δ y ( θ j , k + 1 2 n + M S j , k + 1 2 n )

3. 稳定性分析和误差估计

引理：设 { a n } ， { b n } 是两个非负数列，并且 { c n } 为单调数列，如果满足：

a n + b n ≤ c n + λ ∑ i = 0 n − 1 a i ( λ > 0 ) ; a 0 + b 0 ≤ c 0 ,

那么就有： a n + b n ≤ c n exp ( n λ ) , n = 0 , 1 , 2 , ⋯ , N 。

定理：非平稳双扩散自然对流方程的有限差分格式(13)~(17)式在 4 Δ t ( | u | + | v | ) ≤ min ( P r , 1 , 1 L e ) 和 4 Δ t max { P r , 1 , 1 L e } ≤ min { Δ x 2 , Δ y 2 } 的条件下是局部稳定的。并且有如下的误差估计：

| u ( x j + 1 2 , y k , t n ) − u j + 1 2 , k n | + | v ( x j , y k + 1 2 , t n ) − v j , k + 1 2 n | + | θ ( x j , y k , t n ) − θ j , k n | + | S ( x j , y k , t n ) − S j , k n | + | p ( x j , y k , t n ) − p j , k n | = O ( Δ t , ( Δ x ) 2 , ( Δ y ) 2 ) (19)

证明：如果满足 P r Δ t / Δ x 2 ≤ 1 4 ， P r Δ t / Δ y 2 ≤ 1 4 ，并且 4 Δ t ( | u | + | v | ) ≤ min ( P r , 1 , 1 L e ) ，即

4 Δ t ( ‖ u ‖ ∞ + ‖ v ‖ ∞ ) ≤ min ( P r , 1 , 1 L e ) ，对于(13)式有

| u j + 1 2 , k n + 1 | ≤ Δ t Δ x ( | p j + 1 , k n | + | p j , k n | ) + ( 1 − 2 P r Δ t Δ x 2 − 2 P r Δ t Δ y 2 ) | u j + 1 2 , k n | + P r Δ t Δ x 2 | u j + 3 2 , k n |     + P r Δ t Δ y 2 ( | u j + 3 2 , k + 1 n | + | u j + 1 2 , k - 1 n | ) + Δ t ε ( | u j + 1 , k n | 2 + | u j , k n | 2 Δ x + | ( u v ) j + 1 2 , k + 1 2 n | + | ( u v ) j + 1 2 , k − 1 2 n | Δ y )     + P r ε Δ t D a | u j + 1 2 , k n | + 1.75 Δ t | u j + 1 2 , k n | 2 + | v j + 1 2 , k n | 2 150 D a ε | u j + 1 2 , k n | + | u j + 1 2 , k n | ≤ 2 Δ t Δ x ‖ p n ‖ ∞ + ( 1 + P r ε Δ t D a + P r 2 ε Δ x + P r 2 ε Δ y + 1.75 P r 4 150 D a ε ) ‖ u n ‖ ∞  

这里 ‖     ⋅     ‖ ∞ 是无穷范数，则可推得

‖ u n + 1 ‖ ∞ ≤ 2 Δ t Δ x ‖ p n ‖ ∞ + ( 1 + P r ε Δ t D a + P r 2 ε Δ x + P r 2 ε Δ y + 1.75 P r 4 150 D a ε ) ‖ u n ‖ ∞ , ( n = 1 , 2 , ⋯ , N ) (20)

因为是p泊松方程，所以 ‖ p n ‖ ∞ 是有界的 [9] 。不妨设 ‖ p n ‖ ∞ ≤ β 1 。

由(20)式可得

‖ u n + 1 ‖ ≤ 2 Δ t Δ x β 1 + ( 1 + P r ε Δ t D a + P r 2 ε Δ x + P r 2 ε Δ y + 1.75 P r 4 150 D a ε ) ‖ u n ‖ ∞ , ( n = 1 , 2 , ⋯ , N ) (21)

(21)式中从1到n相加，可得

‖ u n ‖ ∞ ≤ 2 n Δ t Δ x β 1 + ‖ u 0 ‖ ∞ + ( 1 + P r ε Δ t D a + P r 2 ε Δ x + P r 2 ε Δ y + 1.75 P r 4 150 D a ε ) ∑ j = 0 n − 1 ‖ u j ‖ ∞ , ( n = 1 , 2 , ⋯ , N ) (22)

由引理1得

‖ u n ‖ ∞ ≤ ( 2 n Δ t Δ x β 1 + ‖ u 0 ‖ ∞ ) exp ( n + n P r ε Δ t D a + n P r 2 ε Δ x + n P r 2 ε Δ y + 1.75 n P r 4 150 D a ε ) , ( n = 1 , 2 , ⋯ , N ) (23)

即当时间T是有限时，数列 { u n } 是局部稳定的，由有限差分稳定定理 [9] 可得数列 { u n } 是收敛的。

同理，差分格式(15)~(17)式按照上述方法可得

‖ v n + 1 ‖ ∞ ≤ 2 Δ t Δ y β 1 + ( 1 + P r ε Δ t D a + P r 2 ε Δ y + P r 2 ε Δ x + 1.75 P r 4 150 D a ε ) ‖ v n ‖ ∞                           + P r R a ‖ θ n ‖ ∞ + P r R a M ‖ S n ‖ ∞ , ( n = 1 , 2 , ⋯ , N ) (24)

‖ θ n + 1 ‖ ∞ ≤ ( 1 + 1 2 Δ x + 1 2 Δ y ) ‖ θ n ‖ ∞ ,               ( n = 1 , 2 , ⋯ , N ) (25)

‖ S n + 1 ‖ ∞ ≤ ( 1 + 1 2 L e Δ x + 1 2 L e Δ y ) ‖ S n ‖ ∞     ,                     ( n = 1 , 2 , ⋯ , N ) (26)

设 ϖ = max { P r ε Δ t D a + P r 2 ε Δ y + P r 2 ε Δ x + 1.75 P r 4 150 D a ε , P r R a + 1 2 Δ x + 1 2 Δ y , P r R a M + 1 2 L e Δ x + 1 2 L e Δ y } 。

由(23)~(25)式可得

‖ v n ‖ ∞ + ‖ θ n ‖ ∞ + ‖ S n ‖ ∞ ≤ ( 1 + ϖ ) ( ‖ v n − 1 ‖ ∞ + ‖ θ n − 1 ‖ ∞ + ‖ S n − 1 ‖ ∞ ) + 2 Δ t Δ y β 1 (27)

(26)式由1加到n，即

‖ v n ‖ ∞ + ‖ θ n ‖ ∞ + ‖ S n ‖ ∞ ≤ ( ‖ v 0 ‖ ∞ + ‖ θ 0 ‖ ∞ + ‖ S 0 ‖ ) exp ( n ϖ ) + 2 n Δ t Δ y β 1 (28)

当时间T是有限时，(26)式不等号右部分是有界的，由有限差分稳定定理 [10] 可得差分格式(23)~(25)是收敛的。

综上所述，非平稳双扩散自然对流问题的交错网格的有限差分格式是局部稳定的。

下证交错网格有限差分格式的截断误差是(19)式。

对于方程(1)，使用泰勒公式在点 ( x j , y k , t n + 1 ) 处展开，可得

u j + 1 2 , k n + 1 − u j − 1 2 , k n + 1 = u j + 1 2 , k n + 1 − u j , k n + 1 + u j , k n + 1 − u j − 1 2 , k n + 1 = Δ x 2 ( ∂ u ∂ x ) j , k n + 1 + 1 2 ！ ( Δ x 2 ) 2 ( ∂ 2 u ∂ x 2 ) j , k n + 1 + 1 3 ！ ( Δ x 2 ) 3 ( ∂ 3 u ∂ x 3 ) j , k n + 1 + ⋯     + Δ x 2 ( ∂ u ∂ x ) j , k n + 1 − 1 2 ！ ( Δ x 2 ) 2 ( ∂ 2 u ∂ x 2 ) j , k n + 1 + 1 3 ！ ( Δ x 2 ) 3 ( ∂ 3 u ∂ x 3 ) j , k n + 1 − ⋯ = Δ x ( ∂ u ∂ x ) j , k n + 1 + ( Δ x ) 3 24 ( ∂ 3 u ∂ x 3 ) j , k n + 1 + ⋯ (29)

v j , k + 1 2 n + 1 − v j , k − 1 2 n + 1 = v j , k + 1 2 n + 1 − v j , k n + 1 + v j , k n + 1 − v j , k − 1 2 n + 1 = Δ y 2 ( ∂ v ∂ y ) j , k n + 1 + 1 2 ！ ( Δ y 2 ) 2 ( ∂ 2 v ∂ y 2 ) j , k n + 1 + 1 3 ！ ( Δ y 2 ) 3 ( ∂ 3 v ∂ y 3 ) j , k n + 1 + ⋯     + Δ y 2 ( ∂ v ∂ y ) j , k n + 1 − 1 2 ！ ( Δ y 2 ) 2 ( ∂ 2 v ∂ y 2 ) j , k n + 1 = Δ y ( ∂ v ∂ y ) j , k n + 1 + ( Δ y ) 3 24 ( ∂ 3 v ∂ y 3 ) j , k n + 1 + ⋯ (30)

将上式插入方程(1)中，可得

[ ∂ u ∂ x + ∂ v ∂ y ] j , k n + 1 = − ( Δ x ) 2 24 ( ∂ 3 u ∂ x 3 ) j , k n + 1 − ( Δ y ) 2 24 ( ∂ 3 v ∂ y 3 ) j , k n + 1 + ⋯

即方程(1)的截断误差为： O ( ( Δ x ) 2 , ( Δ y ) 2 ) 。

对于方程(2)，使用泰勒公式在点 ( x i + 1 2 , y k , t n ) 处展开，可得

u j + 1 2 , k n + 1 − u j + 1 2 , k n = Δ t ( ∂ u ∂ t ) j + 1 2 , k n + 1 2 ! ( Δ t ) 2 ( ∂ 2 u ∂ t 2 ) j + 1 2 , k n + ⋯ (31)

p j + 1 , k n − p j , k n = ( p j + 1 , k n − p j + 1 2 , k n ) + ( p j + 1 2 , k n − p j , k n ) = Δ x 2 ( ∂ p ∂ x ) j + 1 2 , k n + 1 2 ! ( Δ x 2 ) 2 ( ∂ 2 p ∂ x 2 ) j + 1 2 , k n + 1 3 ! ( Δ x 2 ) 3 ( ∂ 3 p ∂ x 3 ) j + 1 2 , k n + ⋯     + Δ x 2 ( ∂ p ∂ x ) j + 1 2 , k n − 1 2 ! ( Δ x 2 ) 2 ( ∂ 2 p ∂ x 2 ) j + 1 2 , k n + 1 3 ! ( Δ x 2 ) 3 ( ∂ 3 p ∂ x 3 ) j + 1 2 , k n − ⋯ = Δ x ( ∂ p ∂ x ) j + 1 2 , k n + ( Δ x ) 3 24 ( ∂ 3 p ∂ x 3 ) j + 1 2 , k n + ⋯ (32)

u j + 3 2 , k n − 2 u j + 1 2 , k n + u j − 1 2 , k n = ( u j + 3 2 , k n − u j + 1 2 , k n ) + ( u j − 1 2 , k n − u j + 1 2 , k n ) = Δ x ( ∂ u ∂ x ) j + 1 2 , k n + ( Δ x ) 2 2 ! ( ∂ 2 u ∂ x 2 ) j + 1 2 , k n + ( Δ x ) 3 3 ! ( ∂ 3 u ∂ x 3 ) j + 1 2 , k n + ( Δ x ) 4 4 ! ( ∂ 4 u ∂ x 4 ) j + 1 2 , k n + ⋯       − Δ x ( ∂ u ∂ x ) j + 1 2 , k n + ( Δ x ) 2 2 ! ( ∂ 2 u ∂ x 2 ) j + 1 2 , k n − ( Δ x ) 3 3 ! ( ∂ 3 u ∂ x 3 ) j + 1 2 , k n + ( Δ x ) 4 4 ! ( ∂ 4 u ∂ x 4 ) j + 1 2 , k n − ⋯ = ( Δ x ) 2 ( ∂ 2 u ∂ x 2 ) j + 1 2 , k n + ( Δ x ) 4 12 ( ∂ 4 u ∂ x 4 ) j + 1 2 , k n + ⋯ (33)

u j + 1 2 , k + 1 n − 2 u j + 1 2 , k n + u j + 1 2 , k − 1 n = ( u j + 1 2 , k + 1 n − u j + 1 2 , k n ) + ( u j + 1 2 , k n − u j + 1 2 , k − 1 n ) = Δ y ( ∂ u ∂ y ) j + 1 2 , k n + ( Δ y ) 2 2 ! ( ∂ 2 u ∂ y 2 ) j + 1 2 , k n + ( Δ y ) 3 3 ! ( ∂ 3 u ∂ y 3 ) j + 1 2 , k n + ( Δ y ) 4 4 ! ( ∂ 4 u ∂ y 4 ) j + 1 2 , k n + ⋯       − Δ y ( ∂ u ∂ y ) j + 1 2 , k n + ( Δ y ) 2 2 ! ( ∂ 2 u ∂ y 2 ) j + 1 2 , k n − ( Δ y ) 3 3 ! ( ∂ 3 u ∂ y 3 ) j + 1 2 , k n + ( Δ y ) 4 4 ! ( ∂ 4 u ∂ y 4 ) j + 1 2 , k n − ⋯ = ( Δ y ) 2 ( ∂ 2 u ∂ y 2 ) j + 1 2 , k n + ( Δ y ) 4 12 ( ∂ 4 u ∂ y 4 ) j + 1 2 , k n + ⋯ (34)

( u 2 ) j + 1 , k n = ( u 2 ) j + 1 2 , k n + Δ x 2 ( 2 u j + 1 2 , k n ) + 1 2 ! ( Δ x 2 ) 2 [ 2 ( ∂ u ∂ x ) j + 1 2 , k n ] + 1 3 ! ( Δ x 2 ) 3 [ 2 ( ∂ 2 u ∂ x 2 ) j + 1 2 , k n ] + ⋯

( u 2 ) j − 1 , k n = ( u 2 ) j + 1 2 , k n − Δ x 2 ( 2 u j + 1 2 , k n ) + 1 2 ! ( Δ x 2 ) 2 [ 2 ( ∂ u ∂ x ) j + 1 2 , k n ] − 1 3 ! ( Δ x 2 ) 3 [ 2 ( ∂ 2 u ∂ x 2 ) j + 1 2 , k n ] + ⋯

( u 2 ) j + 1 , k n − ( u 2 ) j , k n = 2 Δ x ( u ) j + 1 2 , k n + ( Δ x ) 3 12 ( ∂ 2 u ∂ x 2 ) j + 1 2 , k n + ⋯ (35)

( u v ) j + 1 2 , k + 1 2 n = ( u v ) j + 1 2 , k n + Δ y 2 [ v j + 1 2 , k n ( ∂ u ∂ y ) j + 1 2 , k n + u j + 1 2 ， k n ( ∂ v ∂ y ) j + 1 2 , k n ]     + 1 2 ! ( Δ y 2 ) 2 [ 2 ( ∂ v ∂ y ∂ u ∂ y ) j + 1 2 , k n + v j + 1 2 , k n ( ∂ 2 u ∂ y 2 ) j + 1 2 , k n + u j + 1 2 , k n ( ∂ 2 v ∂ y 2 ) j + 1 2 , k n ]     + 1 3 ! ( Δ y 2 ) 3 [ 3 ( ∂ 2 v ∂ y 2 ∂ u ∂ y ) j + 1 2 , k n + 3 ( ∂ v ∂ y ∂ 3 u ∂ y 3 ) j + 1 2 , k n + v j + 1 2 , k n ( ∂ 3 u ∂ y 3 ) j + 1 2 , k n     + u j + 1 2 , k n ( ∂ 3 v ∂ y 3 ) j + 1 2 , k n ] + ⋯

( u v ) j + 1 2 , k − 1 2 n = ( u v ) j + 1 2 , k n − Δ y 2 [ v ( ∂ u ∂ y ) j + 1 2 , k n + u ( ∂ v ∂ y ) j + 1 2 , k n ]     + 1 2 ! ( Δ y 2 ) 2 [ 2 ( ∂ v ∂ y ∂ u ∂ y ) j + 1 2 , k n + v j + 1 2 , k n ( ∂ 2 u ∂ y 2 ) j + 1 2 , k n + u j + 1 2 , k n ( ∂ 2 v ∂ y 2 ) j + 1 2 , k n ]     − 1 3 ! ( Δ y 2 ) 3 [ 3 ( ∂ 2 v ∂ y 2 ∂ u ∂ y ) j + 1 2 , k n + 3 ( ∂ v ∂ y ∂ 3 u ∂ y 3 ) j + 1 2 , k n v j + 1 2 , k n ( ∂ 3 u ∂ y 3 ) j + 1 2 , k n     + u j + 1 2 , k n ( ∂ 3 v ∂ y 3 ) j + 1 2 , k n ] + ⋯

( u v ) j + 1 2 , k + 1 2 n − ( u v ) j + 1 2 , k − 1 2 n = Δ y [ v ( ∂ u ∂ y ) j + 1 2 , k n + u ( ∂ v ∂ y ) j + 1 2 , k n ] + ( Δ y ) 3 24 ! [ 3 ( ∂ 2 v ∂ y 2 ∂ u ∂ y ) j + 1 2 , k n       + 3 ( ∂ v ∂ y ∂ 2 u ∂ y 2 ) j + 1 2 , k n + v j + 1 2 , k n ( ∂ 3 u ∂ y 3 ) j + 1 2 , k n + u j + 1 2 , k n ( ∂ 3 v ∂ y 3 ) j + 1 2 , k n ] + ⋯ (36)

将(31)~(36)式代入到方程(2)中，可得

∂ u ∂ t + ∂ p ∂ x − P r ( ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 ) + 1 ε ( ∂ ( u 2 ) ∂ x + ∂ ( u v ) ∂ y ) + P r ε D a u + 1.75 u u 2 + v 2 150 D a ε = − 1 4 ( Δ t ) ( ∂ 2 u ∂ t 2 ) j + 1 2 , k n − ( Δ x ) 2 24 ( ∂ 3 p ∂ x 3 ) j + 1 2 , k n + P r [ ( Δ x ) 2 12 ( ∂ 4 u ∂ x 4 ) j + 1 2 , k n + ( Δ y ) 2 12 ( ∂ 4 u ∂ y 4 ) j + 1 2 , k n ]       − 1 ε [ ( Δ x ) 3 12 ( ∂ 2 u ∂ x 2 ) j + 1 2 , k n ] − P r ε D a u j + 1 2 , k n − 1.75 u j + 1 2 , k n ( u 2 ) j + 1 2 , k n + ( v 2 ) j + 1 2 , k n Δ x 150 D a ε       − 1 ε [ ( Δ y ) 2 24 ( 3 ( ∂ 2 v ∂ y 2 ∂ u ∂ y ) j + 1 2 , k n + 3 ( ∂ v ∂ y ∂ 2 u ∂ y 2 ) j + 1 2 , k n + v j + 1 2 , k n ( ∂ 3 u ∂ y 3 ) j + 1 2 , k n + u j + 1 2 , k n ( ∂ 3 v ∂ y 3 ) j + 1 2 , k n ) ] + ⋯

即方程(2)的截断误差为： O ( Δ t , ( Δ x ) 2 , ( Δ y ) 2 ) 。

同理可得，方程(3)~方程(5)的截断误差为： O ( Δ t , ( Δ x ) 2 , ( Δ y ) 2 ) 。

即非平稳双扩散自然对流方程的交错网格有限差分格式的截断误差为(19)式得证。

4. 数值模拟

下面给出数值算例说明上述交错网格有限差分格式的有效性和可行性。

在双扩散自然对流方程(1)~(5)中取 P r = 0.7 , L e = 2.0 , M = 1 , D a = 10 − 3 , R a = 10 3 , ε = 1 ，初边值条件为(6)~(12)，并取空间步长为 Δ x = Δ y = 0.01 ，时间步长为 Δ t = 10 − 4 。用交错网格差分格式(13)~(18)求得双扩散自然对流问题的数值解，将各个时刻的流线、温度和浓度分布状况画在图2中。图3描述的是在 t = 0.5 时刻浮力比 M = − 50 , 1 , 50 的流线、温度和浓度分布状况，浮力比 M ( − 50 ≤ M ≤ 50 ) 是溶质浮力与热浮力之间的比值。从图3可以看出，由于腔体的左壁是持续均匀加热的，所以流体会沿着顺时针方向从左壁向冷却的右壁转动。当M从−50增加到1，流函数的值减小，即流体的流量减少，流线集中在腔体壁附近且腔体的中心是空的。 M = 50 时，温度和浓度的变化主要集中在右臂的下侧和左壁的上侧，表明流体的变化主要是由于热传导导致的，这归结于热边界层厚度的增加；当M增加到1时，热量分散到了右壁；当M进一步增加到50时，温度和浓度的变化主要集中在冷却的右壁。对于低浮力比的情况，整个墙体受流体结构的影响，即随着浮力比增加，边界层厚度越薄。在高浮力比情况下，这种流体结构的变化对浓度场产生显著影响，即在墙体周围形成了垂直分层现象。与已发表的工作成果相比较，流体的运动、温度场和浓度场的变化基本吻合，不同浮力比情况下的流体的运动模式也很一致。

5. 结论

本文运用有限差分方法对非平稳双扩散自然对流问题进行了研究，构造了双扩散自然对流方程的交

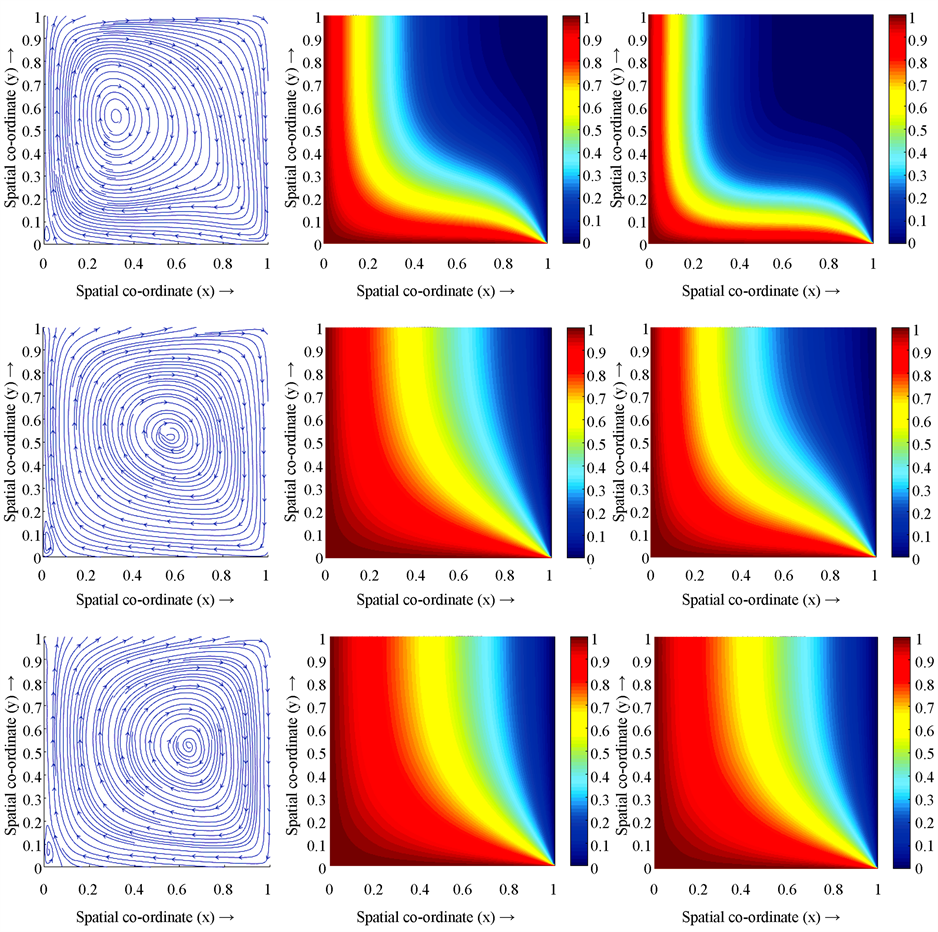
Figure 2. When M = 1 , streamlines, isotherms, isoconcentrations at t = 0.05 , 0.2 , 0.5 , in order from top to bottom

图2. M = 1 时，从上到下依次是 t = 0.05 , 0.2 , 0.5 时的流线图，温度图，浓度图

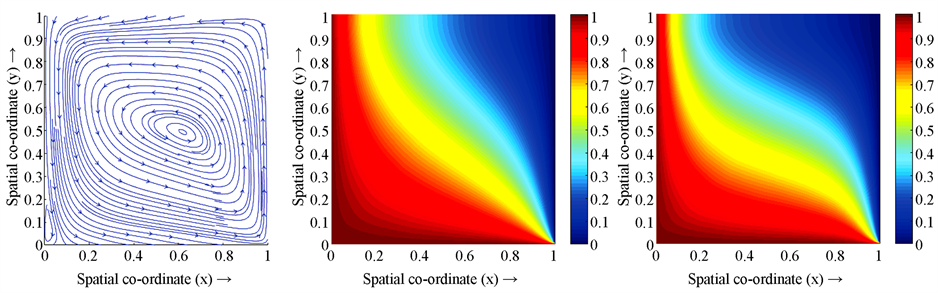
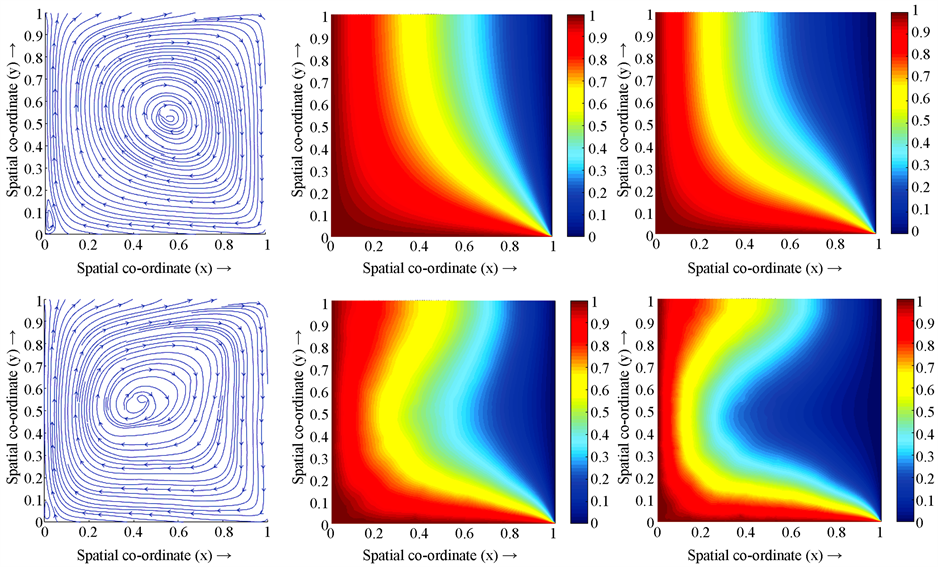
Figure 3. When t = 0.5 , streamlines, isotherms, isoconcentrations at M = − 50 , 1 , 50 , in order from top to bottom

图3. t = 0.5 时，从上到下依次是 M = − 50 , 1 , 50 的流线图，温度图，浓度图

错网格有限差分格式，并做了稳定性分析、给出了差分格式的误差估计。最后，利用所构造的有限差分格式进行编程计算，模拟充满多孔介质的方形腔体中流场、温度场、浓度场随时间的变化状况，并讨论了浮力比对流场、温度场、浓度场的影响。数值结果与已发表的工作成果相比具有很好的一致性，进一步表明了交错网格有限差分格式计算非平稳双扩散自然对流问题的有效性和可行性。

文章引用

蔡志飞. 多孔介质中非平稳双扩散自然对流的有限差分法
A Finite Difference Method for Unsteady Double-Diffusive Natural Convection in Porous Medium[J]. 应用数学进展, 2018, 07(08): 1008-1019. https://doi.org/10.12677/AAM.2018.78118

参考文献

  1. 1. 陈宝明, 王补宣, 方肇洪. 多孔介质自然对流中温度梯度与浓度梯度的相互耦合[J]. 工程热物理学报, 1995, V16(2): 210-214.

  2. 2. 竺可桢. 物理学[M]. 北京: 科学出版社, 1973: 1-3.

  3. 3. Nield, D.A. and Bejan, A. (2013) Convection in Porous Media. 4th Edition, Springer, New York. https://doi.org/10.1007/978-1-4614-5541-7

  4. 4. Basak, T., Roy, S., Matta, A. and Pop, I. (2010) Analysis of Heatline for Natural Convection within Porous Trapezoidal Enclosures: Effect of Uniform and Non-Uniform Heating of Bottom Wall. International Journal of Heat and Mass Transfer, 53, 5947-5961. https://doi.org/10.1016/j.ijheatmasstransfer.2010.07.026

  5. 5. Sathiyamoorthy, M., Basak, T. and Roy, S. (2011) Non-Darcy Buoyancy Flow in a Square Cavity Filled with Porous Medium for Various Temperature Difference Aspect Ratios. Journal of Porous Media, 14, 649-657. https://doi.org/10.1615/JPorMedia.v14.i7.80

  6. 6. Roy, S., Basak, T., Thirumalesha, Ch. and Murali Krishna, Ch. (2008) Finite Element Simulation on Natural Convection Flow in a Triangular Enclosure Due to Uniform and Nonuniform Bottom Heating. Journal of Heat Transfer, 130, Article Number: 032501. https://doi.org/10.1115/1.2804934

  7. 7. Nithiarasu, P., Seetharamu, K.N. and Sundarararjan, T. (1997) Natural Convective Heat Transfer in a Fluid Saturated Variable Porosity Medium. International Journal of Heat and Mass Transfer, 40, 3955-3967. https://doi.org/10.1016/S0017-9310(97)00008-2

  8. 8. Mahapatra, T.R., Pal, D. and Mondal, S. (2013) Effects of Buoyancy Ratio on Double-Diffusive Natural Convection in a Lid-Driven Cavity. International Journal of Heat and Mass Transfer, 57, 771-785. https://doi.org/10.1016/j.ijheatmasstransfer.2012.10.028

  9. 9. 张文生. 科学计算中的偏微分方程有限差分法[M]. 北京: 高等教育出版社, 2006.

  10. 10. Chung, T. (2002) Computational Fluid Dynamics. Cambridge University Press, Cambridge, 1036. https://doi.org/10.1017/CBO9780511606205

期刊菜单