Advances in Applied Mathematics
Vol.
07
No.
10
(
2018
), Article ID:
27212
,
9
pages
10.12677/AAM.2018.710145
The Transformed Rational Method for Solving Two Extended (3 + 1)-Dimensional Jimbo-Miwa Equations
Jinting Ha1, Xue Guan2, Huiqun Zhang1
1Department of Mathematics and Statistics, Qingdao University, Qingdao Shandong
2School of Science, Beijing University of Posts and Telecommunications, Beijing

Received: Oct. 1st, 2018; accepted: Oct. 15th, 2018; published: Oct. 22nd, 2018

ABSTRACT
In this paper, two extended (3 + 1)-dimensional Jimbo-Miwa equations can be researched with the transformed rational function method. As a result, new exact travelling wave solutions for two extended (3 + 1)-dimensional Jimbo-Miwa equations are obtained by means of Maple software. What’s more, if we choose different ordinary differential equations, we can obtain different types of travelling wave solutions which supplement the existing literatures.
Keywords:(3 + 1)-Dimensional Jimbo-Miwa Equation, Transformed Rational Function Method, New Exact Travelling Wave Solutions
有理函数变换法求解两类扩展的(3 + 1)维Jimbo-Miwa方程
哈金婷1,关雪2,张辉群1
1青岛大学,数学与统计学院,山东 青岛
2北京邮电大学理学院,北京

收稿日期:2018年10月1日;录用日期:2018年10月15日;发布日期:2018年10月22日

摘 要
在本文中,我们引入有理函数变换法对两类扩展的(3 + 1)维Jimbo-Miwa方程进行了研究。通过这种方法并借助于Maple软件得到了它们新的行波精确解,而且如果我们选择不同的常微分方程,还可以得到不同类的行波解,补充了以往文献的研究成果。
关键词 :(3 + 1)维Jimbo-Miwa方程,有理函数变换法,新的行波精确解

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
非线性发展方程在科学工程领域是一个研究热点,引起了学者们的广泛关注。值得注意的是,学者们借助丰富的研究手段求解了非线性发展方程比如Korteweg-de Vries方程,Boiti-Pempinelli-Tu方程和sine-Gordon方程等。研究方法多种多样,有齐次平衡法 [1] [2] ,李对称分析 [3] [4] [5] ,F展开法 [6] ,Jacobi椭圆函数法 [7] ,指数函数法 [8] [9] ,反散射变换法 [10] [11] 等。近几年,马文秀教授提出了一种能够有效得到非线性发展方程新行波解的方法,有理函数变换法 [12] 。这个方法不仅能够系统地得到新的行波解,还统一了指数函数法,齐次平衡法,扩展的双曲函数展开法,Jacobi椭圆函数展开法,F展开法,映射法等。在本文中,我们通过有理函数变换法得到了两类扩展的(3 + 1)维JM方程的新行波解。
KP可积族中的第二个方程为(3 + 1)维JM方程 [13] ,
(1)
其中, 。
(3 + 1)维JM方程(1)已经被许多方法所研究,比如扩展的有理函数变换法 [14] ,扩展的Tanh方法 [15] ,Hirtoa双线性法 [16] [17] ,多指数函数法 [18] ,有理函数变换法 [12] ,Bell多项式法 [19] 等。由于(3 + 1)维JM方程好的可积性质,它可以被扩展成如下的方程,
(2)
和
(3)
显然,(1)中的线性项 和 分别扩展成(2)中的 和(3)中的 。据我们所知,在文献 [20] 中,通过简化的Hirota方法得到了两类扩展的(3 + 1)维JM方程的多孤子解。在文献 [21] [22] 中,基于双线性形式得到了它们的lump解和lump-kink解。在文献 [23] 中,通过complex方法得到了(2)和(3)的亚纯解。
本文分为以下内容,在第二部分我们简单介绍有理函数变换法的基本步骤。第三部分和第四部分依据有理函数变换法研究了两类扩展的有理函数变换法,然后借助于符号计算得到了相应的研究结果。第四部分我们对本文进行了总结。
2. 有理函数变换法
在这一部分我们介绍有理函数变换法的基本思想,考虑非线性偏微分方程
(4)
其中 是一个关于 的函数。
首先作行波变换 ,k和c是任意的实常数,则(4)变为下面的常微分方程,
(5)
其中 ,且r是方程(5)中的最低阶导数。
假设
(6)
且 满足一阶微分方程
(7)
其中m,n是自然数, , 是待定常数,通过选择满足不同常微分方程的 ,方程(4)的行波解并且许多求解方法得到了统一。
3. 第一类扩展的(3 + 1)维Jimbo-Miwa方程
第一类扩展的(3 + 1)维Jimbo-Miwa方程为
(8)
首先作行波变换 , 是波数, 是波频。可将方程(8)约化为下面的常微分方程,
(9)
其中(9)中的各阶导数表示u关于 求导。
然后对方程(9)关于 积分并取积分常数为0得
(10)
设 , ,我们得到了方程(8)的变换形式,
(11)
3.1. 当 时
(11)可以变成
(12)
平衡(12)中的最高阶导数项和最高阶非线性项,有 。为了计算方便,我们取 ,借助于符号计算,得到了(12)的有理解v,
(13)
和
(14)
由于 满足一阶常微 ,所以第一类扩展的(3 + 1)维Jimbo-Miwa方程的指数函数行波解为
和
d为积分常数,其余的参数均为任意常数。
3.2. 当 时
(11)可以变成
(15)
平衡(15)中的最高阶导数项和最高阶非线性项,有 。我们取 ,借助于符号计算,得到了(15)的有理解v,
(16)
和
(17)
由于 和 均满足一阶常微 ,所以第一类扩展的(3 + 1)维Jimbo-Miwa方程的双曲函数行波解为
和
d为积分常数,其余的参数均为任意常数。
3.3. 当 时
(11)可以变成
(18)
平衡(18)中的最高阶导数项和最高阶非线性项,有 。类似地,我们取 ,借助于符号计算,得到了(18)的有理解v,
(19)
和
(20)
由于 满足一阶常微 ,则第一类扩展的(3 + 1)维Jimbo-Miwa方程的周期行波解为
和
d为积分常数,其余的参数均为任意常数。
3.4. 当 时
(11)可以变成
(21)
我们取 ,借助于符号计算,得到了(27)的有理解v,
(22)
和
(23)
由于 满足一阶常微 ,则第一类扩展的(3 + 1)维Jimbo-Miwa方程的有理解为
和
d为积分常数,其余的参数均为任意常数。
4. 第二类扩展的(3 + 1)维Jimbo-Miwa方程
第二类扩展的(3 + 1)维Jimbo-Miwa方程为
(24)
首先作行波变换 , 是波数, 是波频。
可将方程(24)约化为下面的常微分方程,
(25)
其中(25)中的各阶导数表示u关于 求导。
然后对方程(25)关于 积分并取积分常数为0,设 , ,我们得到了变换的扩展JM方程
(26)
4.1. 当 时
(26)可以变成
(27)
平衡(27)中的最高阶导数项和最高阶非线性项,有 。为了计算方便,我们取 ,借助于符号计算,得到了(27)的有理解v,
(28)
和
(29)
由于 满足一阶常微 ,因此第二类扩展的(3 + 1)维Jimbo-Miwa方程的指数函数行波解为
和
d为积分常数,其余的参数均为任意常数。
4.2. 当 时
(26)可以变成
(30)
方程(30)的有如下的有理解v,
(31)
和
(32)
由于 和 均满足一阶常微 ,因此第二类扩展的(3 + 1)维Jimbo-Miwa方程的双曲函数行波解为
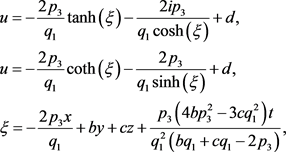
和
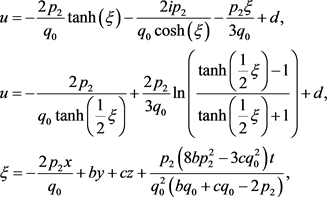
d为积分常数,其余的参数均为任意常数。
4.3. 当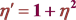 时
时
第二类扩展的(3 + 1)维Jimbo-Miwa方程的周期行波解为

和

d为积分常数,其余的参数均为任意常数。
4.4. 当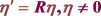 时
时
第二类扩展的(3 + 1)维Jimbo-Miwa方程的有理解为
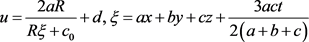
和
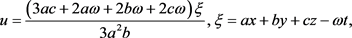
d为积分常数,其余的参数均为任意常数。
5. 结论
在本文中,我们借助于符号计算研究了两类扩展的(3 + 1)维Jimbo-Miwa方程,得到了丰富的行波精确解。如果选择的 满足其他形式的常微分方程,我们就可以得到更加多样化的行波精确解。值得注意的是,有理函数变换法可以用来求解其它的非线性方程,且扩展的有理函数变换法还可以得到孤子方程的复合解 [24] 。
满足其他形式的常微分方程,我们就可以得到更加多样化的行波精确解。值得注意的是,有理函数变换法可以用来求解其它的非线性方程,且扩展的有理函数变换法还可以得到孤子方程的复合解 [24] 。
文章引用
哈金婷,关雪,张辉群. 有理函数变换法求解两类扩展的(3 + 1)维Jimbo-Miwa方程
The Transformed Rational Method for Solving Two Extended (3 + 1)-Dimensional Jimbo-Miwa Equations[J]. 应用数学进展, 2018, 07(10): 1247-1255. https://doi.org/10.12677/AAM.2018.710145
参考文献
- 1. Wang, M.L. (1995) Solitary Wave Solutions for Variant Boussinesq Equations. Physics Letters A, 199, 169-172. https://doi.org/10.1016/0375-9601(95)00092-H
- 2. Wang, M.L. (1996) Exact Solutions for a Compound KdV-Burgers Equation. Physics Letters A, 213, 279-287. https://doi.org/10.1016/0375-9601(96)00103-X
- 3. Bluman, G.W. and Kumei, S. (1989) Symmetries and Differential Equations. Springer-Verlag, Berlin. https://doi.org/10.1007/978-1-4757-4307-4
- 4. Cantwell, B.J. (2002) Introduction to Symmetry Analysis. Cambridge University Press, Cambridge.
- 5. Dong, H.H., et al. (2016) A New Integrable Symplectic Map and the Lie Point Symmetry Associated with Nonlinear Lattice Equations. Journal of Nonlinear Sciences and Applications, 9, 5107-5118. https://doi.org/10.22436/jnsa.009.07.13
- 6. Zhou, Y.B., Wang, M.L. and Wang, Y.M. (2003) Periodic Wave Solutions to a Coupled KdV Equations with Variable Coefficients. Physics Letters A, 208, 31-36. https://doi.org/10.1016/S0375-9601(02)01775-9
- 7. Liu, S.K., et al. (2001) Jacobi Elliptic Function Expansion Method and Periodic Wave Solutions of Nonlinear Wave Equations. Physics Letters A, 289, 69-74. https://doi.org/10.1016/S0375-9601(01)00580-1
- 8. He, J.H. and Wu, H.X. (2006) Exp-Function Method for Nonlinear Wave Equations. Chaos Solitons Fractals, 30, 700-708. https://doi.org/10.1016/j.chaos.2006.03.020
- 9. He, J.H. and Abdou, M.A. (2007) New Periodic Solutions for Nonlinear Evolution Equations Using Exp-Function Method. Chaos Solitons Fractals, 34, 1421-1429. https://doi.org/10.1016/j.chaos.2006.05.072
- 10. Ablowitz, M.J. and Segur, H. (1981) Solitons and the Inverse Scattering Transform. SIMA, Philadephia. https://doi.org/10.1137/1.9781611970883
- 11. Novikov, S.P., Manakov, S.V., Pitaevskii, L.P. and Zakharov, V.E. (1984) Theory of Solitons: The Inverse Scattering Method. Springer-Verlag, Berlin.
- 12. Ma, W.X. and Lee, J.H. (2009) A Transformed Rational Function Method and Exact Solutions to the (3 + 1)-Dimensional Jimbo-Miwa Equation. Chaos Solitons Fractals, 42, 1356-1363. https://doi.org/10.1016/j.chaos.2009.03.043
- 13. Jimbo, M. and Miwa, T. (1983) Solitons and Infnite Dimensional Lie Algebras. Publications of Research Institute for Mathematical Sciences, 19, 943-1001. https://doi.org/10.2977/prims/1195182017
- 14. Zhang, H.Q. and Ma, W.X. (2014) Extended Transformed Rational Function Method and Applications to Complexiton Solutions. Applied Mathematics Computation, 230, 509-515. https://doi.org/10.1016/j.amc.2013.12.156
- 15. Hong, W.P. and Oh, K.S. (2000) New Solitonic Solutions to a (3 + 1)-Dimensional Jimbo-Miwa Equation. Computers & Mathematics with Applications, 39, 29-31. https://doi.org/10.1016/S0898-1221(00)00043-2
- 16. Wazwaz, A.M. (2008) Multiple-Soliton Solutions for the Calogero-Bogoyavlenskii-Schiff, Jimbo-Miwa and YTSF Equations. Applied Mathematics Computation, 203, 592-597. https://doi.org/10.1016/j.amc.2008.05.004
- 17. Yang, J.Y. and Ma, W.X. (2017) Abundant Lump-Type Solutions of the Jimbo-Miwa Equation in (3 + 1)-Dimensions. Computers & Mathematics with Applications, 73, 220-225. https://doi.org/10.1016/j.camwa.2016.11.007
- 18. Zhang, L., Lin, Y.Z. and Liu, Y.P. (2014) New Solitary Wave Solutions for Two Nonlinear Evolution Equations. Computers & Mathematics with Applications, 67, 1595-1606. https://doi.org/10.1016/j.camwa.2014.02.017
- 19. Singh, M. and Gupta, R.K. (2016) Bäcklund Transformations, Lax System, Conservation Laws and Multisoliton Solutions for Jimbo-Miwa Equation with Bell-Polynomials. Communications in Nonlinear Science and Numerical Simulation, 37, 362-373. https://doi.org/10.1016/j.cnsns.2016.01.023
- 20. Wazwaz, A.M. (2017) Multiple-Soliton Solutions for Extended (3 + 1)-Dimensional Jimbo Miwa Equations. Applied Mathematics Letters, 64, 21-26. https://doi.org/10.1016/j.aml.2016.08.005
- 21. Sun, H.Q. and Chen, A.H. (2017) Lump and Lump-Kink Solutions of the (3 + 1)-Dimensional Jimbo-Miwa and Two Extended Jimbo-Miwa Equations. Applied Mathematics Letters, 68, 55-61. https://doi.org/10.1016/j.aml.2016.12.008
- 22. Li Y.Z. and Liu, J.G. (2018) Abundant Lump and Lump-Kink Solutions for the Extended (3 + 1)-Dimensional Jimbo-Miwa Equation. Nonlinear Dynamics, 91, 497-504. https://doi.org/10.1007/s11071-017-3884-4
- 23. Li, H. and Li, Y.Z. (2018) Meromorphic Exact Solutions of Two Extended (3 + 1)-Dimensional Jimbo-Miwa Equations. Applied Mathematics Computation, 333, 369-375. https://doi.org/10.1016/j.amc.2018.03.099
- 24. Zhang, H.Q. and Ma, W.X. (2014) Extended Transformed Rational Function Method and Applications to Complexiton Solutions. Applied Mathematics and Computation, 230, 509-515. https://doi.org/10.1016/j.amc.2013.12.156