Advances in Applied Mathematics
Vol.
08
No.
10
(
2019
), Article ID:
32653
,
8
pages
10.12677/AAM.2019.810189
Weighted C-N Scheme of Homogeneous Fractional Diffusion Equations and Its Correction
Zhu Chen, Fenghui Huang*
Department of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Oct. 1st, 2019; accepted: Oct. 17th, 2019; published: Oct. 24th, 2019

ABSTRACT
For the homogeneous time fractional diffusion equation, the accuracy of the numerical method will decrease when the exact solution is not smooth enough. In this case, we consider a weighted Crank-Nicolson scheme (masked as weighted C-N scheme) and its correction. After correcting the first step of the weighted C-N scheme, the second-order time accuracy can be restored. Then we give the detailed convergence analysis, and numerical examples verify the effectiveness of the scheme.
Keywords:Time Fractional Diffusion Equation, Crank-Nicolson Scheme, Convergence
齐次分数阶扩散方程的加权C-N格式及其修正
陈著,黄凤辉*
华南理工大学数学学院,广东 广州

收稿日期:2019年10月1日;录用日期:2019年10月17日;发布日期:2019年10月24日

摘 要
对于齐次时间分数阶扩散方程,在精确解不光滑时,数值方法精度会下降。针对这种情况,本文提出加权Crank-Nicolson格式(简记为加权C-N格式)及其修正格式,在精确解不光滑时,修正原格式的第1步后,可恢复方法的时间2阶精度。本文接着给出详细的收敛性分析,并且数值算例验证了方法的有效性。
关键词 :时间分数阶扩散方程,Crank-Nicolson格式,收敛性

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
分数阶微分方程的数值方法的精度常依赖于精确解的光滑性。针对精确解不光滑的情况,许多学者开始研究数值方法的修正格式,以保持离散格式的高精度。例如,Lubich [1] [2] [3] 给出基于1阶和2阶向后差分格式的两种修正方法,并给出收敛性分析。Yan [4] [5] 考虑L1格式的修正格式,并提出基于分段2次插值
本文考虑如下齐次分数阶扩散方程:
(1)
其中 , 是Caputo时间分数阶导数,其定义为:
(2)
算子A表示有界正则区域上的自伴正定二阶椭圆偏微分算子 [4],满足
(3)
其中 表示 范数,记 为Riemman-Liouville导数,则有 。
2. 加权C-N格式及其修正格式
令 ,则方程(1)可表示为:
(4)
令 为时间步长, ,h为空间步长, 。 表示 的向后Euler卷积逼近,其生成函数为:
(5)
分数阶导数的逼近格式在 时刻的时间精度为1阶,在 时刻的时间精度为2阶,对 在 时刻和 时刻作线性拉格朗日插值,可得 时刻的逼近格式 。带入方程(4),可得加权C-N格式:
(6)
在精确解不光滑的情况下,加权C-N格式达不到2阶时间精度。我们对加权C-N格式(6)的第1步得初值条件添加一个权系数
,适当选取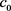 可使离散格式保持2阶精度,加权C-N修正格式如下:
可使离散格式保持2阶精度,加权C-N修正格式如下:
(7)
3. 加权C-N修正格式的收敛性分析
为了证明加权C-N修正格式的收敛性分析,我们先给出3个引理。
引理1:定义式子:
(8)
本文统一令 , [1],当权系数 时,则有:
(9)
其中C为正常数。
证明:令 ,,则 ,,,所以 ,即可证得 。
引理2:定义式子:
(10)
(11)
则下式成立:
(12)
(13)
其中 表示 范数,C为正常数。
证明:令 ,则 时, ,所以 ,即 。
由引理1可得 ,将 带入式(3)可得:
(14)
(15)
且下式成立:
(16)
带入式(10)即可证得式(12)和(13):
(17)
(18)
引理3: 分别由引理1和引理2定义,则下式成立:
(19)
证明:令
,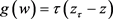 ,则
,,,所以可得
,即:
,则
,,,所以可得
,即:
(20)
由 ( [8] 引理B.1),且由式(16)及可得:
(21)
其中 ,即证得引理3。
为了给出收敛性分析,接下来我们分别借助Laplace变换和Cauchy积分公式,给出齐次分数阶扩散方程(4)的精确解和加权C-N修正格式(7)的数值解。对方程(4)作Laplace变换可得:
(22)
对式(21)作Laplace逆变换可得方程(4)的精确解:
(23)
其中 , [4]。
考虑加权C-N修正格式(7),式子两边同乘 ,并关于n求和, ,令 ,于是 ,由式(5)可得:
(24)
(25)
令 ,由Cauchy积分公式及式(8)、(10)和(11)可得加权C-N修正格式的数值解:
(26)
定理1 分别为 时刻方程(4)的精确解和加权C-N修正格式(7)的数值解,则下式成立:
(27)
证明: ,而 ,由引理1和引理2可得:
(28)
接着考虑 ,令 ,c为正常数,则:
(29)
(30)
则可证得 ,即权系数取 时,加权C-N修正格式为时间2阶精度。
4. 数值算例
数值算例1:考虑如下齐次分数阶扩散方程:
(31)
该方程的精确解为 ,u在 时不光滑。不同时间步长的误差如表1所示,不同 下的误差与对应步长的对数关系如图1所示,其中空间步长取 ,统一取离散误差为 误差 。
Table 1. L 2 error of weighted C-N scheme (6) and weighted C-N modified scheme (7)
表1. 加权C-N格式(6)和加权C-N修正格式(7)的 误差
表1给出不同 及不同时间步长取值下,两种方法所得的误差。方法(a)为加权C-N格式离散,方法(b)为加权C-N修正格式离散,由表1可以看出,两种格式误差均收敛,且修正后的误差更小,方法更精确。
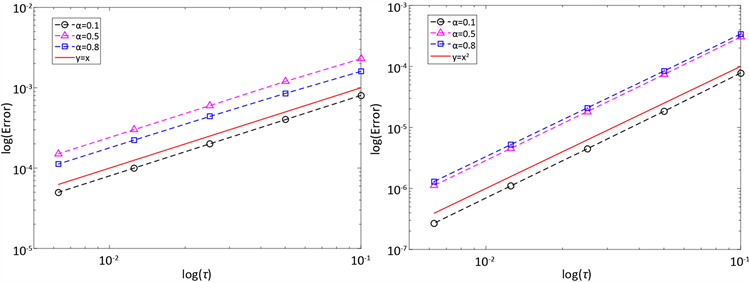
Figure 1. The relationship between error and time step
图1. 误差与时间步长的关系
图1给出不同 下误差与时间步长的关系,两坐标均为对数坐标,其中图1(a)为加权C-N格式,图1(b)为加权C-N修正格式。正如理论证明的结果一样,加权C-N格式只有1阶时间精度,而修正后的格式可达到2阶时间精度。
数值算例2:考虑如下齐次分数阶扩散方程:
(32)
该方程的精确解为 ,u在 时不光滑。取 ,不同时间步长下的两种格式的误差和精度如表2所示。
Table 2. Error and time accuracy of weighted C-N scheme (6) and weighted C-N modified scheme (7)
表2. 加权C-N格式(6)和加权C-N修正格式(7)的误差和时间精度
由表2可以看出,随着时间步长减小,两方法的误差均减小,但加权C-N格式只有1阶时间精度,而修正格式的精度可达到2阶。
基金项目
国家自然科学基金青年科学基金项目(61802129),广东省国家青年基金纵向协同项目(2018A030310381)。
文章引用
陈 著,黄凤辉. 齐次分数阶扩散方程的加权C-N格式及其修正
Weighted C-N Scheme of HomogeneousFractional Di?usion Equations and Its Correction[J]. 应用数学进展, 2019, 08(10): 1611-1618. https://doi.org/10.12677/AAM.2019.810189
参考文献
- 1. Lubich, C., Sloan, I.H. and Thomee, V. (1996) Nonsmooth Data Error Estimates for Approximations of an Evolution Equation with a Positive-Type Memory Team. Mathematics of Computation, 65, 1-17.
https://doi.org/10.1090/S0025-5718-96-00677-1 - 2. Lubich, C. (2004) Convolution Quadrature Revisited. Bit Numerical Mathematics, 44, 503-514.
https://doi.org/10.1023/B:BITN.0000046813.23911.2d - 3. Cuesta, E., Lubich, C. and Palencia, C. (2006) Convolution Quadrature Time Discretization of Fractional Diffusion-Wave Equations. Mathematics of Computation, 75, 673-696.
https://doi.org/10.1090/S0025-5718-06-01788-1 - 4. Yan, Y.B., Khan, M. and Ford, N.J. (2018) An Analysis of the Modified L1 Scheme for Time-Fractional Partial Differential Equations with Nonsmooth Data. SIAM Journal on Numerical Analysis, 56, 210-227.
https://doi.org/10.1137/16M1094257 - 5. Xing, Y.Y. and Yan, Y.B. (2018) A Higher Order Numerical Method for Time Fractional Partial Differential Equations with Nonsmooth Data. Journal of Computational Physics, 357, 305-323.
https://doi.org/10.1016/j.jcp.2017.12.035 - 6. Tadjeran, C., Meerschaert, M.M. and Scheffler, H.P. (2006) A Second-Order Accurate Numerical Approximation for the Fractional Diffusion Equation. Journal of Computational Physics, 213, 205-213.
https://doi.org/10.1016/j.jcp.2005.08.008 - 7. Jin, B.T., Lazarov, R. and Zhou, Z. (2018) An Analysis of the Crank-Nicolson Method for Subdiffusion. IMA Journal of Numerical Analysis, 38, 518-541.
https://doi.org/10.1093/imanum/drx019 - 8. Jin, B.T., Lazarov, R. and Zhou, Z. (2017) Correction of High-Order BDF Convolution Quadrature for Fractional Evolution Equations. SIAM Journal on Scientific Computing, 39, A3129-A3152.
https://doi.org/10.1137/17M1118816
