Advances in Applied Mathematics
Vol.
08
No.
12
(
2019
), Article ID:
33352
,
6
pages
10.12677/AAM.2019.812222
Relaxation Oscillations Analysis in a Predator-Prey System of Leslie Type
Chenrong Pan, Songlin Chen
School of Mathematical Science and Engineering, Anhui University of Technology, Ma’anshan Anhui

Received: Nov. 9th, 2019; accepted: Dec. 2nd, 2019; published: Dec. 9th, 2019

ABSTRACT
In this paper, we consider a predator-prey system of Leslie type with functional response. The equilibrium point type and stability of the system are analyzed, and the existence and uniqueness of relaxation oscillation period of the system are proved by using the entry-exit function and geometric singular perturbation theory.
Keywords:Leslie Predator-Prey System, Entry-Exit Function, Geometric Singular Perturbation Theory, Existence and Uniqueness
Leslie型捕食者–食饵系统的弛豫振荡分析
潘陈蓉,陈松林
安徽工业大学数理科学与工程学院,安徽 马鞍山

收稿日期:2019年11月9日;录用日期:2019年12月2日;发布日期:2019年12月9日

摘 要
在本文中,我们考虑一个具有功能反应的Leslie型捕食者–食饵系统。分析系统的平衡点类型和稳定性,利用入–出函数和几何奇异摄动理论证明了系统的弛豫振荡周期的存在唯一性。
关键词 :Leslie型捕食者–食饵系统,入–出函数,几何奇异摄动理论,存在唯一性

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
考虑如下具有功能反应的Leslie型捕食者–食饵系统 [1] :
(1)
其中, ,表示捕食者的摄取率作为食饵密度的函数 [2]。 ,对所有的 ,使得 ,因此,对于所有的 ,有 。x表示食饵种群的密度;y表示捕食者种群的密度;r和s都是正数,分别表示食饵和捕食者的内在增长率; ,表示食饵的环境承载力; 是支撑一个捕食者所需的食饵数量。根据生态系统的意义,我们在区域 上讨论 [3]。
近几年来,Jicai Huang等人研究了由Holling III型功能反应产生的Leslie型捕食者–食饵系统的分支 [1]。Claudia Valls等人研究了修正的Leslie-Gower模型的非线性震荡 [4]。Yanfei Dai等人研究了由Holling III型功能反应产生的Leslie型捕食者–食饵系统的四个极限环 [2]。本文研究具有功能反应的Leslie型捕食者–食饵系统的弛豫振荡。
对系统(1)作变换:
(2)
将 仍记为 ,则系统(1)可以化为:
(3)
2. 研究背景
2.1. 系统(3)的平衡点分析
对于任意的参数,系统(3)有一个双曲鞍点 ,它是一个边界平衡点。这个边界平衡点的生态学解释是:当缺乏捕食者时,食饵种群达到它的环境承载能力 [5]。研究系统(3)的正平衡点个数,我们能够得到下面的结论。
引理2.1:令 ,和 。
1) 如果 ,则系统(3)有一个基本的正平衡点;
2) 如果 ,并且
2.1) ,则系统(3)有两个不同的正平衡点:一个是基本的正平衡点,另一个是退化的正平衡点;
2.2) ,则系统(3)有一个正平衡点,并且为退化的正平衡点;
3)如果 ,且 ,则系统(3)有三个不同的基本的正平衡点。
2.2. 入–出函数
考虑慢–快平面系统:
(4)
其中, 是状态–空间变量, 表示时间尺度的比例,且 。假设函数f和g是足够平滑的,并且满足下列条件:
 (5)
(5)
当 时,解从点 开始,其中, ,解快速地被吸引到x轴,然后沿着x轴向右漂移,最后被x轴排斥。它在x轴上的一点 重新相交于直线 。当 时, 。其中 由下面的公式决定。
(6)
函数 被式(6)隐式地定义,函数 被称为入–出函数 [6]。
2.3. 极限系统的动力学
考虑慢–快系统,根据几何奇异摄动理论 [7] 知,系统(3)是慢–快系统的快时间尺度公式。令 ,得到慢–快系统的慢时间尺度公式为:
(7)
令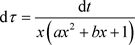 ,当
时,有
。从而得到:
,当
时,有
。从而得到:
(8)
系统(8)有一个平凡平衡点 ,和一个边界平衡点 。令 ,得到相关联的快系统为:
(9)
系统(9)具有快零点曲线 ,和慢零点曲线 。零点曲线不依赖于 。在式(8)和式(9)中,令 ,分别得到慢–快系统的慢子系统和快子系统:
(10)
和
(11)
慢子系统(10)的动力学受限于y轴和临界曲线:
(12)
对于快子系统(11),y轴和临界曲线 由平衡点组成。
3. 弛豫振荡
令 和 ,则(9)变为:
(13)
注意:(a)对于任意的 ,。即对于 ,在y轴正轴上有 。其中在 处, 从负数变为正数。即对于快子系统(11),当通过曲线 时,y轴正轴从排斥变为吸引。
(b)当 时,有 。其中, 为一般的折点, ,。
基于上述分析,我们得到下面的结果。
引理3.1:对于系统(13),存在唯一的 ( ),使得
(14)
引理3.1的证明:在系统(13)中,对于 ,有
(15)
和
(16)
并且有
(17)
和
(18)
综上可得,存在唯一的 ( ),使得
引理得证。
对于 附近的 ,我们定义 ( ),由公式 ,得到 。
命题3.2:如果
,且
是充分小的参数,
是
的一个充分小的邻域,则系统(9)通过
的解首先与直线
相交于点
。在
拓扑中,当 时,
。
时,
。
定理3.3:对于一个固定的参数 ,使得 和 ,在S中,存在一个邻域U,使得对于小参数 ,系统(13)在U中有唯一的闭轨 , 是双曲吸引的,并且在Hausdorff拓扑 [8] 中,当 时, 接近于S。
定理3.3的证明:利用Fenechel理论 [9] 描述抛物线吸引部分附近的流动,文献 [10] 中分析了抛物线折点附近的流动。对于小参数 ,我们利用式(9)定义映射 。其中, 是 的一个充分小的邻域。由文献 [11] 得知,存在常数 ,使得 的 C1 范数是 的阶。则对于小参数 ,我们利用 定义 。利用 定义庞加莱映射 。由命题3.3和上述分析得, 是一个收缩映射。
致谢
感谢审稿老师及编辑老师提出的宝贵意见。
文章引用
潘陈蓉,陈松林. Leslie型捕食者–食饵系统的弛豫振荡分析
Relaxation Oscillations Analysis in a Predator-Prey System of Leslie Type[J]. 应用数学进展, 2019, 08(12): 1937-1942. https://doi.org/10.12677/AAM.2019.812222
参考文献
- 1. Huang, J.C., Ruan, S.G. and Song, J. (2014) Bifurcations in a Predator-Prey System of Leslie Type with Generalized Holling Type III Functional Response. Journal of Differential Equations, 257, 1721-1752.
- 2. Dai, Y.F., Zhao, Y.L. and Sang, B. (2019) Four Limit Cycles in a Predator-Prey System of Leslie Type with Generalized Holling Type III Functional Response. Nonlinear Analysis: Real World Applications, 50, 218-239.
- 3. 卜令杰, 窦霁虹, 刘萌萌, 邢伟. 一类三次系统极限环的存在唯一性[J]. 延安大学学报(自然科学版), 2014, 33(2): 1-5.
- 4. Valls, C. (2019) Nonlinear Oscillations in the Modified Leslie-Gower Model. Nonlinear Analysis: Real World Applications, 51, 1-7.
- 5. 林园, 高瑾. Lotka-Volterra竞争扩散系统连接边界平衡点和正平衡点行波解的存在性[J]. 教育教学论坛, 2019(27): 95-98.
- 6. Maesschalck, P.D. and Schecter, S. (2016) The Entry-Exit Function and Geometric Singular Perturbation Theory. Journal of Differential Equations, 260, 6697-6715.
https://doi.org/10.1016/j.jde.2016.01.008 - 7. Lee, M.G. and Tzavaras, A. (2017) Existence of Localizing Solutions in Plasticity via Geometric Singular Perturbation Theory. SIAM Journal on Applied Dynamical Systems, 16, 337-360.
https://doi.org/10.1137/16M1087308 - 8. 王国俊. Lukasiewicz语义集上的紧Hausdorff拓扑[J]. 数学学报, 2002, 45(5): 919-924.
- 9. Panazzolo, D. and Da Silva, P.R. (2017) Regularization of Discontinuous Foliations: Blowing up and Sliding Conditions via Fenichel Theory. Journal of Differential Equations, 263, 8362-8390.
https://doi.org/10.1016/j.jde.2017.08.042 - 10. Krupa, M. and Szmolyan, P. (2001) Extending Geometric Singular Perturbation Theory to Nonhyperbolic Points-Fold and Canard Points in Two Dimensions. SIAM Journal on Mathematical Analysis, 33, 286-314.
https://doi.org/10.1137/S0036141099360919 - 11. Krupa, M. and Szmolyan, P. (2001) Relaxation Oscillation and Canard Explosion. Journal of Differential Equations, 174, 312-368.
https://doi.org/10.1006/jdeq.2000.3929