Advances in Applied Mathematics
Vol.
09
No.
10
(
2020
), Article ID:
38064
,
9
pages
10.12677/AAM.2020.910197
利用Laplace变换求解时间分数阶对流扩散方程
时旭1,2,崔晨1,刘佳奇1
1华侨大学数学科学学院,福建 泉州
2重庆大学光电工程学院,重庆
收稿日期:2020年9月26日;录用日期:2020年10月8日;发布日期:2020年10月15日

摘要
本文提出了求解时间分数阶对流扩散方程两种高效数值算法。首先基于Laplace变换及指数变换将原问题转化为整数阶扩散问题;然后采用Crank-Nicolson格式并分别结合二阶中心差分和四阶紧致差分方法,设计出两种求解时间分数阶对流扩散方程的高精度差分格式,并利用Fourier方法证明两种差分格式都是稳定的。数值实验验证了两种格式的有效性。
关键词
时间分数阶对流扩散方程,Laplace变换,指数变换,二阶中心差分格式,四阶紧致差分格式
Solving Time Fractional Convection-Diffusion Equation Using Laplace Transform
Xu Shi1,2, Chen Cui1, Jiaqi Liu1
1School of Mathematical Sciences, Huaqiao University, Quanzhou Fujian
2College of Optoelectronic Engineering, Chongqing University, Chongqing
Received: Sep. 26th, 2020; accepted: Oct. 8th, 2020; published: Oct. 15th, 2020

ABSTRACT
This paper proposes two efficient numerical algorithms for solving the time fractional convection-diffusion equation. First, the original problem is transformed into an integer-order diffusion problem based on Laplace transform and exponential transform. Then, using Crank-Nicolson format and combining second order central difference and fourth order compact difference respectively, two kinds of high precision difference formats for solving time fractional order convection-diffusion equations are designed, and both schemes are proved to be stable by using Fourier method. Numerical experiments verify the effectiveness of the two formats.
Keywords:Time Fractional Order Convection-Diffusion Equation, Laplace Transform, Exponential Transformation, Second Order Central Difference Scheme, Fourth Order Compact Difference Scheme

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在研究分子扩散、粘性流体运动及物质运输过程等问题时,经常要根据实际情况建立起相应的对流扩散方程来求解。特别是分数阶对流扩散方程,有时更能准确刻画物质的运动规律、描述一些物理现象。因此,设计出比较稳定的数值格式来求解时间分数阶对流扩散方程一直备受人们的关注,具有极为重要的理论意义和实际意义。
本文研究如下的时间分数阶对流扩散方程:
(1)
国内外学者们对分数阶导数、整数阶对流扩散方程及分数阶对流扩散方程进行了许多重要研究。如陈焕贞等 [1] 详细梳理了分数阶扩散模型方面的理论和数值模拟方面的进展和动态;Ren等 [2] 提出了一种用Laplace变换近似分数阶项的方法;李娴娟等 [3] 把谱方法用于求解分数阶偏微分方程在空间和时间方向上的离散,还用最优误差估计证明了该方法的收敛性,并用数值结果验证了理论分析;王玉娇等 [4] 讨论了分数阶导数的数值解法以及其在生物力学方面的一些应用;叶俊杰等 [5] 研究了一种求解Riemann-Liouville型分数阶微分方程的微分变换方法;董建强等 [6] 使用样条插值和帕德逼近设计了一种求解一维对流扩散方程具有高精度的紧致差分格式;郭非凡等 [7] 研究了变系数分数阶对流扩散方程的一种有限差分方法;刘扬等 [8] 构造了一种严格对角占优的Crank-Nicolson有限差分格式来求解一维非定常对流扩散方程;黄素珍等 [9] 通过指数变换、反指数变换和待定系数法,建立了一种三层差分格式来求解一维对流扩散方程;宋光珍 [10] 针对时间分数阶扩散方程初边值问题给出了两种高精度数值格式;余跃玉 [11] 针对变系数时间分数阶对流扩散方程设计出一种隐式有限差分格式,并给出格式差分解存在性与唯一性的证明;王学彬等 [12] 给出了两种常见分数阶导数的Laplace变换公式,同时给出了具体实例来说明如何使用Laplace变换;覃平阳等 [13] 提出一种隐式差分格式;张艳等 [14] 通过Laplace变换得出了分数阶微分方程Mittag-Leffler函数形式解析解;沈淑君等 [15] 讨论了时间、空间及时空方向的分数阶对流扩散方程的解法;常娟等 [16] 设计出一种高阶紧致指数型差分格式来求解对流扩散方程,并采用具有并行性的AGE迭代法对其求解。
本文利用Laplace变换逼近时间分数阶对流扩散方程的分数阶项,将其转化为整数阶问题,然后分别通过二阶中心差分格式和四阶紧致差分格式求方程的数值解。
2. 时间分数阶对流扩散方程的数值解
2.1. 利用Laplace变换将分数阶问题转化为整数阶问题
针对方程(1),首先使用Laplace变换逼近方程的分数阶导数:
(2)
其中, 是 的Laplace变换。由于 ,故可以将 线性化:
(3)
将(3)式代入到(2)式中可得(4)式:
(4)
再由Laplace逆变换,可得:
(5)
于是,原时间分数阶对流扩散方程可转化为如下的整数阶方程(6):
(6)
引入指数变换:
(7)
将(7)带入方程(6)整理可得:
(8)
令 ,,有:
(9)
2.2. 二阶中心差分格式
以 表示时间步长,以h表示空间步长。网格点为 ,其中 ,。
考虑方程(9)在 时刻的值并对于时间和空间导数均利用中心差分,可得:
(10)
式中:
(11)
(12)
项中 以第k + 1层和第k层的算数平均值代替,代入(10)式并略去高阶无穷小项,得到二阶中心差分格式:
(13)
2.3. 四阶紧致差分格式
为了进一步改进上述算法的空间精度,我们引入如下的padé逼近:
(14)
考虑方程(9)在 时刻的值并对于时间和空间导数项分别利用中心差分和上述padé逼近,可得:
(15)
并略去高阶无穷小项,得到如下四阶紧致差分格式:
(16)
3. 稳定性分析
下面我们将利用Fourier分析法,给出上述两种格式的稳定性分析。
定理1. 对于任意 ,差分格式(13)是无条件稳定的。
证明:利用Fourier分析法,令 ,得:
由此得到增长因子:
于是:
定理2. 对于任意 ,差分格式(22)是无条件稳定的。
证明:利用Fourier分析法,令 ,得:
由此得到增长因子:
于是:
易证 ,那么恒有 。从而此差分格式无条件稳定。
4. 数值算例
在本章,我们通过具体的数值算例来验证两种差分格式的有效性和准确性。首先,定义如下的最大相对误差:
其中, 为方程的精确解, 为方程的数值解( )。
4.1. 算例一
考虑如下时间分数阶对流扩散方程:
其中,
表1,表2给出了不同时空步长、不同 下的两种格式的最大相对误差。对比数据可以发现当 接近1或0时,数值解精度越高,而且在剖分数较少的情况下,格式2比格式1具有更高的精度。
Table 1. Example 1: Maximum relative error of the second-order central difference scheme
表1. 算例一:二阶中心差分格式最大相对误差
Table 2. Example 1: Maximum relative error of the fourth-order central difference scheme
表2. 算例一:四阶中心差分格式最大相对误差
图1给出了两种格式在 分别取0.3和0.8时的真实解图像和误差图像。

Figure 1. When alpha is 0.3 and 0.8, the numerical solution image of the first equation and the error image of the two formats
图1. 分别取0.3和0.8时算例一方程的数值解图像和两种格式的误差图像
4.2. 算例二
考虑如下时间分数阶对流扩散方程:
其中,
表3,表4给出了不同时空步长、不同α下的两种格式的最大相对误差。通过数据对比可以得到类似例一的结论。
Table 3. Example 2: Maximum relative error of the second-order central difference scheme
表3. 算例二:二阶中心差分格式最大相对误差
Table 4. Example 2: Maximum relative error of the fourth-order central difference scheme
表4. 算例二:四阶中心差分格式最大相对误差
图2给出了两种格式在α分别取0.3和0.8时的真实解图像和误差图像。
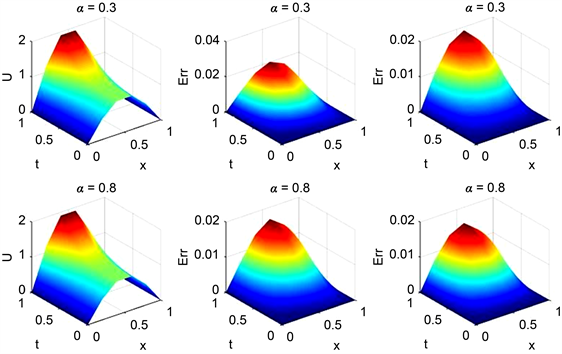
Figure 2. When alpha is 0.3 and 0.8, the numerical solution image of the second equation and the error image of the two formats
图2. 分别取0.3和0.8时算例二方程的数值解图像和两种格式的误差图像
5. 结论
基于Laplace变换和有限差分方法,本文提出了两种求解时间分数阶对流扩散方程的高效数值算法,证明了格式的无条件稳定性。数值实验表明,四阶紧致差分格式比二阶中心差分格式具有更高的计算效率和精度优势。与此同时,Laplace变换的使用限制了算法的精度,我们下一步将对此变换做进一步的改进。
基金项目
国家自然科学基金青年项目(11701196,11701197)资助。
文章引用
时 旭,崔 晨,刘佳奇. 利用Laplace变换求解时间分数阶对流扩散方程
Solving Time Fractional Convection-Diffusion Equation Using Laplace Transform[J]. 应用数学进展, 2020, 09(10): 1701-1709. https://doi.org/10.12677/AAM.2020.910197
参考文献
- 1. 陈焕贞, 杨素香, 刘思宇. 分数阶扩散模型数值模拟的研究进展[J]. 山东师范大学学报(自然科学版), 2019, 34(2): 127-136.
- 2. Ren, J.C., Sun, Z.Z. and Dai, W.Z. (2016) New Approximations for Solving the Caputo-Type Fractional Partial Differential Equations. Applied Mathematical Modelling, 40, 2625-2636. https://doi.org/10.1016/j.apm.2015.10.011
- 3. 李娴娟. 分数阶偏微分方程的理论和数值研究[D]: [博士学位论文]. 厦门: 厦门大学, 2009.
- 4. 王玉娇. 分数阶导数及其应用[D]: [硕士学位论文]. 太原: 太原理工大学, 2014.
- 5. 叶俊杰, 钱德亮. Riemann-Liouville型分数阶微分方程的微分变换方法[J]. 应用数学与计算数学学报, 2009, 23(2): 111-120.
- 6. 董建强, 罗传胜, 李春光, 景何仿. 基于样条插值求解对流扩散方程[J]. 数学的实践与认识, 2019, 49(8): 193-200.
- 7. 郭非凡, 张新东, 王硕. 时间分数阶变系数对流扩散方程的数值解法[J]. 山东科学, 2020, 33(1): 116-123.
- 8. 刘扬. 对流扩散方程的新型Crank-Nicholson差分格式[J]. 数学杂志, 2005(4): 463-467.
- 9. 黄素珍. 求解一维对流扩散方程的一种三层有限差分格式[J]. 盐城工学院学报(自然科学版), 2009, 22(1): 22-25.
- 10. 宋光珍. 时间分数阶扩散方程的两种数值解法[D]: [博士学位论文]. 青岛: 青岛大学, 2016.
- 11. 余跃玉. 变系数时间分数阶对流扩散方程的数值解法[J]. 北华大学学报(自然科学版), 2019, 20(1): 15-20.
- 12. 王学彬. 拉普拉斯变换方法解分数阶微分方程[J]. 西南师范大学学报(自然科学版), 2016, 41(7): 7-12.
- 13. 覃平阳, 张晓丹. 空间–时间分数阶对流扩散方程的数值解法[J]. 计算数学, 2008(3): 305-310.
- 14. 张艳, 黄震, 叶萌, 李泽妤. 利用分数阶微分方程模拟一维热传导问题[J]. 北京建筑工程学院学报, 2013, 29(4): 62-64.
- 15. 沈淑君. 分数阶对流–扩散方程的基本解和数值方法[D]: [博士学位论文]. 厦门: 厦门大学, 2008.
- 16. 常娟, 田芳. 求解对流扩散方程的一种新方法[J]. 宁夏师范学院学报, 2007(6): 33-35.
