Journal of Image and Signal Processing
Vol.05 No.01(2016), Article ID:16770,10
pages
10.12677/JISP.2016.51005
Two 3D Morphological Filtering Methods Based on Sphere Structuring Element
Bin Zhang1,2, Xiancheng Mao1,2*
1MOE Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Central South University, Changsha Hunan
2School of Geosciences and Info-Physics, Central South University, Changsha Hunan

Received: Dec. 29th, 2015; accepted: Jan. 12th, 2016; published: Jan. 15th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
3D morphological filtering based on mathematical morphology can become very time-consuming when using a large-scale structuring element involving the operation; however, if the structuring element is sphere, the Euclidean distance transform (EDT) could be used to perform basic morphological operations instead. Taking some geologic body as a case study, the comparison analysis results show that two filtering methods based on sphere structuring element have the same effects, whereas, the method based on EDT is more effective and applicable for large-scale structuring element involved.
Keywords:3D Morphological Filtering, Sphere Structuring Element, Mathematical Morphology, Euclidean Distance Transform

基于球形结构元素的两种三维形态滤波方法
张彬1,2,毛先成1,2*
1中南大学有色金属成矿预测教育部重点实验室,湖南 长沙
2中南大学地球科学与信息物理学院,湖南 长沙

收稿日期:2015年12月29日;录用日期:2016年1月12日;发布日期:2016年1月15日

摘 要
基于数学形态学的三维形态滤波在采用大规模结构元素进行运算时,变得异常耗时,若采用的结构元素为球形,则可以使用欧式距离变换代替基本的形态学运算。以某地质体二值图像为背景,对两种三维形态滤波方法进行对比分析,实验结果表明,基于球形结构元素的两种形态滤波方法的滤波效果完全相同,但基于欧式距离变换的形态滤波方法在针对大规模球形结构元素时更为有效。
关键词 :三维形态滤波,球形结构元素,数学形态学,欧式距离变换

1. 引言
形态滤波是从数学形态学 [1] [2] 中发展出来的一种新型的非线性滤波技术,相对于传统的频域滤波等数字滤波技术,形态滤波只取决于信号的局部形状特征,因而在诸如形状分析、模式识别、视觉校验等方面更为有效。基于数学形态学的形态滤波,采用具有一定形态的结构元素去量度和提取图像中的对应形状以达到图像分析与识别的目的 [3] - [5] ,其中,结构元素的选取至关重要,形态滤波结果直接取决于结构元素的形态和规模。
随着三维建模技术的广泛发展,三维图像变得越来越普及,传统的图像处理则更多地从二维领域转向三维领域 [6] [7] 。采用基于数学形态学的方法能够很好的解决三维图像的非线性形态探测问题,但是从形态滤波运算时间上考虑,它不但取决于目标图像的规模,还取决于结构元素的规模。尤其当我们为了获取更平滑的趋势形态,往往需要采用大规模的结构元素以滤除更多的不相关结构,由于三维图像本身的复杂性和规模大的特点,这将导致运算异常耗时。
欧式距离变换 [8] - [10] 产生的距离图像包含了每一像素距其最邻近特征(背景)像素之间的欧式距离。针对欧式距离变换的特殊性质,可以从距离图像中提取出相对原始图像一定范围内的腐蚀或膨胀图像,对比于数学形态学中的腐蚀与膨胀运算,若采用的结构元素为球形,则二者结果完全一致,因此可以采用基于欧式距离变换的形态滤波方法,提取目标物体的趋势形态,并且大幅度地减小了计算量。
在采用球形结构元素的前提下,本文将传统的基于数学形态学的滤波方法转化为基于欧式距离变换的方法。选用安徽省铜陵凤凰山矿田新屋里岩体 [11] 作为分析目标,对其进行二值化处理,得到新屋里岩体的二值图像,分别运用两种形态滤波方法对得到的图像进行滤波处理,对滤波结果和运算时间进行分析,比较两种方法的优缺点和适用性。
2. 基于数学形态学的方法
2.1. 数学形态学
数学形态学是由G. Matheron和J. Serra于六十年代中建立的 [12] ,最初被用于洛林铁矿的矿相学定量描述和云母页岩的气孔网络描述,现被广泛应用于计算机视觉、计算机绘图及数字图像处理领域。数学形态学有着严格的集合理论基础,其基于集合运算的处理方法,使其独立于其它滤波方法,可处理任何维度的复杂形态物体的滤波问题,具有形式简单,且易于实现的优点。
在数学形态学的运算过程中,常需要借助一定形态的结构元素,也可称之为探针,对目标物体进行形态探测。基本的数学形态学算子包括膨胀,腐蚀以及开运算和闭运算 [13] 。为了说明这四个基本运算的特点,以A表示输入图像,B表示结构元素,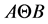 表示B对A的腐蚀,
表示B对A的腐蚀,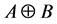 表示B对A的膨胀,
表示B对A的膨胀,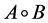 表示B对A的开变换,
表示B对A的开变换,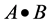 表示B对A的闭变换。那么,
表示B对A的闭变换。那么,
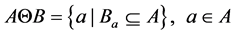 (1)
(1)
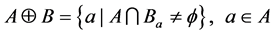 (2)
(2)
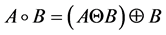 (3)
(3)
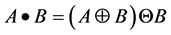 (4)
(4)
式中Ba是关于B对a向量的平移操作,从上述表达式可以看出,腐蚀变换要求对于A中所有点a,Ba完全包含于A,因此,腐蚀会消除图像中孤立的点和毛刺,从而使原始图像缩小。膨胀与腐蚀互为对偶运算,膨胀运算可由腐蚀运算的补集来定义,膨胀运算可以填补图像中的小孔和裂隙,从而使原始图像扩大。形态学开运算和闭运算则是由基本的腐蚀与膨胀的组合来定义,通过顺序组合腐蚀与膨胀运算,开运算和闭运算可以达到先腐蚀(膨胀)缩小(扩大),然后再进行一定程度的恢复,从而达到滤波的功能。
2.2. 滤波方法描述
虽然形态学开运算和闭运算可以达到基础滤波的功能,但一般场合下,通过组合开闭或闭开滤波算子可以达到更好的滤波效果,能够同时滤除图像中的小于结构元素的凸起与凹陷。本文选择先执行闭运算后执行开运算的闭开滤波变换,
 (5)
(5)
对地质体对象进行滤波处理。图1中,原始图像模拟地质体表面包含各种褶皱和超覆现象(图1(a)),使用球形结构元素进行滤波,开运算相当于球体在地质体内边界滚动以削平地质体凸峰(图1(b)和图1(c)),闭运算相当于球体在地质体外边界滚动以填补地质体的凹谷(图1(d)和图1(e)),使用闭开滤波的运算效果见图1(f)。


 (a) 原始图像 (b) 开运算 (c) 开运算效果
(a) 原始图像 (b) 开运算 (c) 开运算效果

 (d) 闭运算 (e) 闭运算效果 (f) 闭开滤波效果
(d) 闭运算 (e) 闭运算效果 (f) 闭开滤波效果
Figure 1. Morphological filtering principles and effects
图1. 形态滤波原理与效果图
结合表达式(3),(4)和(5)可以看出,闭开滤波的基本运算还是腐蚀与膨胀运算,因此,只需要分析出腐蚀与膨胀运算的实现算法即可。图2模拟了使用球形结构元素对地质体的腐蚀与膨胀操作过程。基于数学形态学的腐蚀与膨胀算法,针对图像中的每一像素与结构元素中的每一像素进行集合运算,以判断该像素点是否应该纳入腐蚀或膨胀集合(图3),具体实现可参见 [13] 。
从上述对腐蚀与膨胀的实现描述可知,结构元素的规模将直接影响滤波运算时间,由于地质体规模本身足够庞大,如果所选用球形结构元素的半径过大,可能会导致运算时间过长而无法接受。
3. 基于欧式距离变换的方法
3.1. 欧式距离变换
距离变换是图像处理领域历史悠久的研究话题。通过对某一图像进行距离变换,生成距离图像,距离图像中的信息则包含了每一像素距其最邻近特征(背景)像素之间的距离,如果这种距离测度表现为欧式距离,则称之为欧式距离变换。现有的欧式距离变换算法主要包括完全欧式距离变换 [14] [15] 和近似欧式距离变换 [16] 两类,前者计算得到的距离值更准确,但复杂度较高。本文采用基于模板扫描的三维带符号的欧式距离变换(3-SEDT)算法 [17] ,该算法计算结果采用距离向量的方式来表达,距离值可由距离向量的模计算得出,具有精度高,复杂度低的优点。
本文为了适应地质体距离场的表示,将3-SEDT算法中8个距离模板扫描方向稍加调整(图4)。设栅格空间大小为L × W × H,分别表示栅格空间的长宽高。3-SEDT初始化方案一般为:所有的特征体素初始距离向量为(0,0,0)向量,其它背景体素初始距离向量为(U,U,U)向量,其中U是一个很大的数,可以理解为无穷大。3-SEDT分自下而上(Upward)和自上而下(Downward)两个过程进行扫描:

Upward process:此过程沿栅格空间自下而上进行扫描,针对k轴的每个平面(From k = 2 to k = H-1),又包含两个子过程:前向(Forward)过程和后向(Backward)过程。前向和后向操作过程分别沿j轴正向和负向进行,此过程可以近似看做是一个2-SEDT,以下给出前向和后向操作步骤:
l Forward process:对每一行体素(From j = 1 to j = W-2),先使用模板1从左到右扫描(From i = 1 to i = L-2),再用模板2对同一行体素从右到左扫描(From i = L-1 to i = 0),该过程自后向前(沿j轴正向)进行,故称作前向过程;
l Backward process:对每一行体素(From j = W-2 to j = 0),先使用模板3从右到左扫描(From i = L-2 to i = 1),再用模板4对同一行体素从左到右扫描(From i = 1 to i = L-1),该过程自前向后(沿j轴负向)进行,故称作后向过程。
Downward Process:此过程沿栅格空间自上而下进行扫描,针对k轴的每个平面(From k = H-2 to k = 0),也包含两个子过程:后向过程和前向过程。这个与自下而上过程是类似的,只是扫描的顺序和方向发生了改变,以下是两个子过程的操作步骤:
l Backward process:对每一行体素(Form j = W-2 to j = 1),先使用模板5从右到左扫描(From i = L-2 to i = 1),再用模板6对同一行体素从左到右扫描(From i = 1 to i = L-1),该过程自前向后(沿j轴负向)进行,故称作后向过程;
l Forward process:对每一行体素(From j = 1 to j = W-1),先使用模板7从左到右扫描(From i = 1 to i = L-2),再用模板8对同一行体素从右到左扫描(From i = L-2 to i = 0),该过程自后向前(沿j轴正向)进行,故称作前向过程。


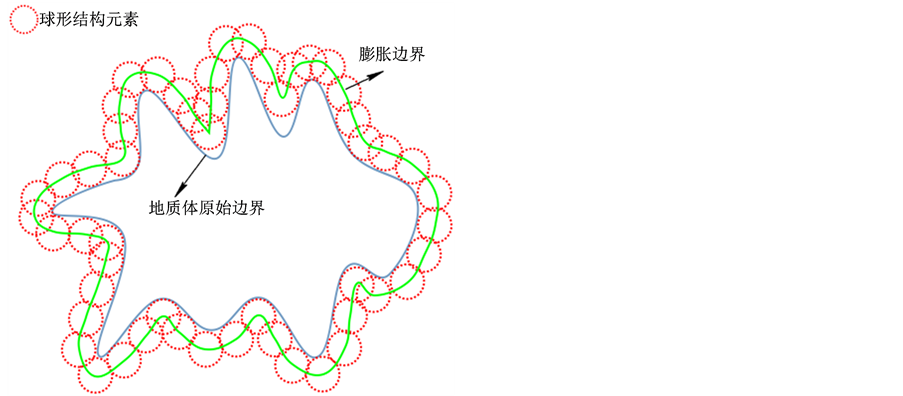 (a) 腐蚀运算 (b) 膨胀运算
(a) 腐蚀运算 (b) 膨胀运算
Figure 2. Erosion and dilation based on mathematical morphology
图2. 基于数学形态学的腐蚀与膨胀
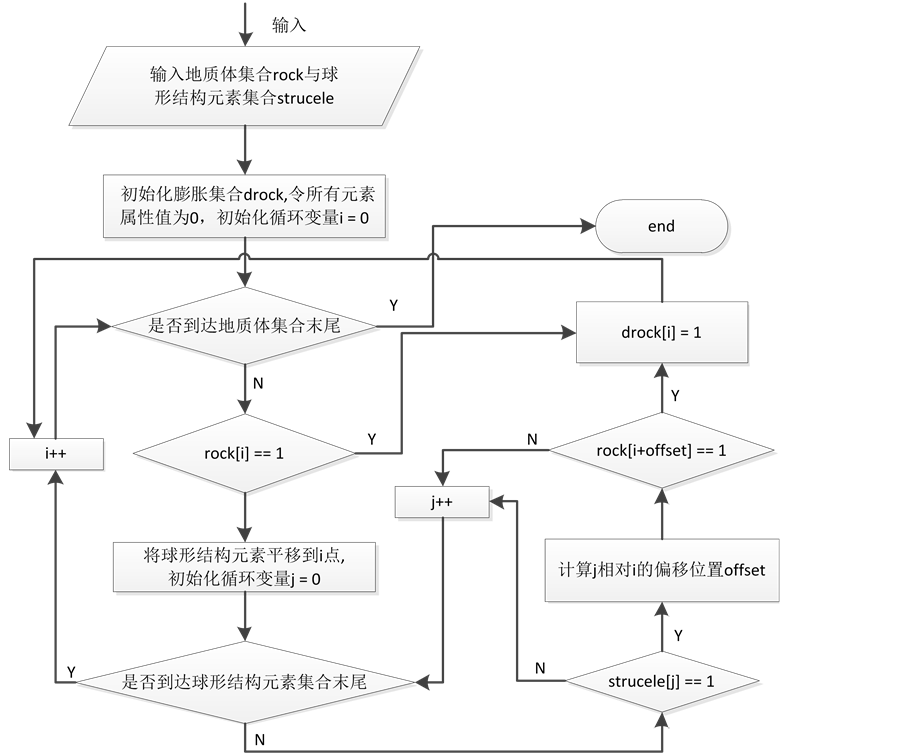
Figure 3. Flow chart of dilation based on mathematical morphology
图3. 基于数学形态学的膨胀流程图
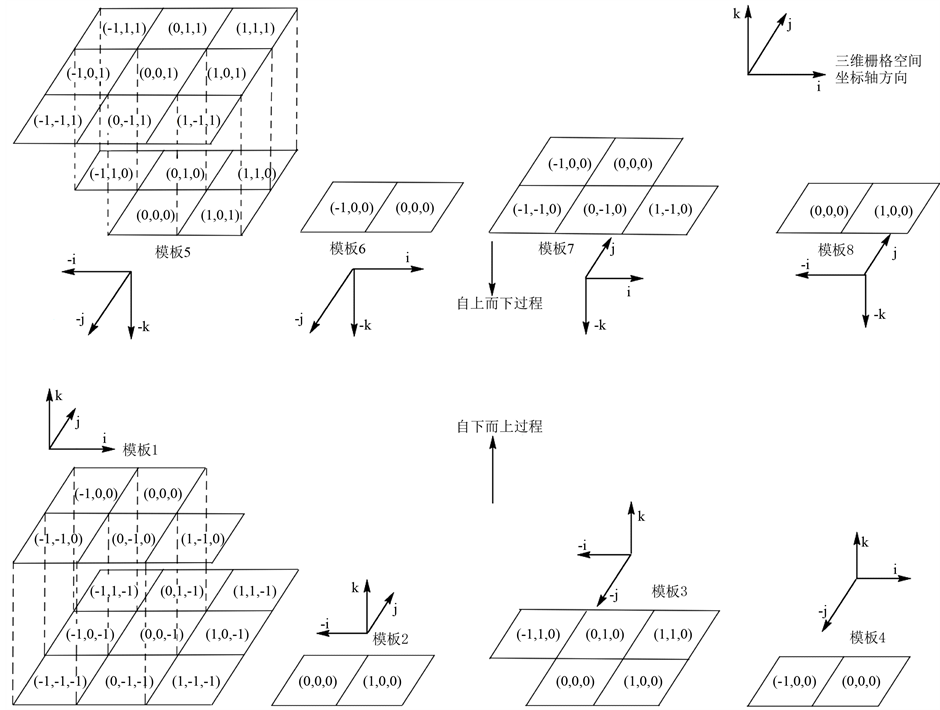
Figure 4. Eight distance templates used in 3-SEDT
图4. 3-SEDT所使用的8个模板
扫描每进行一步,需要对中心体素(模板中0向量所对应的栅格空间中的某一体素)作如下运算,以得到新的距离向量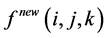 :
:
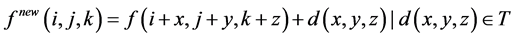 (6)
(6)
要求其中的向量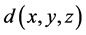 满足
满足
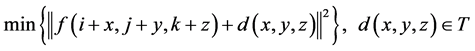 (7)
(7)
此时右边加法计算得到的向量才是新距离向量。表达式(6)中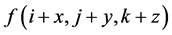 实际上是模板中
实际上是模板中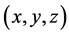 向量所对应中心体素周围体素的距离向量。
向量所对应中心体素周围体素的距离向量。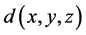 为模板中
为模板中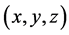 向量,T为模板空间,包含若干模板距离向量。
向量,T为模板空间,包含若干模板距离向量。
三维带符号的欧式距离变换,这里的“符号”有正负之分,指的是生成的距离场有内外之分。在三维地质空间中,以地质体表面为界,在地质体外部生成的距离场为正欧式距离场;在地质体内部生成的距离场为负欧式距离场。它们的计算方法相同,只是初始化方案不同,在正距离场的计算中,地质体空间所代表的三维二值图像中,岩体部分即属性值为1的部分,初始化距离向量为0向量,其余空白部分即属性值为0的部分初始化为无穷向量;而在负距离场的计算中则相反,岩体部分初始化距离向量为无穷向量,其余空白部分初始化为0向量。下面以正欧式距离场的计算为例,介绍三维地质体对象欧式距离场的生成步骤:

Step 1:准备地质体模型。建立要进行欧式距离变换的地质体的三维二值图像;
Step 2:距离场初始化。三维正欧式距离场初始化方案:将三维二值图像中的特征体元初始距离向量赋为(0,0,0)向量,将其它所有背景体元初始距离向量赋为无穷向量。
Step 3:三维欧式距离变换。利用已经定义好的8个距离模板在整个三维图像内进行扫描变换(此过程详见 [17] )。
Step 4:写距离场文件。(距离场文件中每个单元存储的都是该体体元距其最邻近特征体元的距离向量的坐标)。

3.2. 滤波方法描述
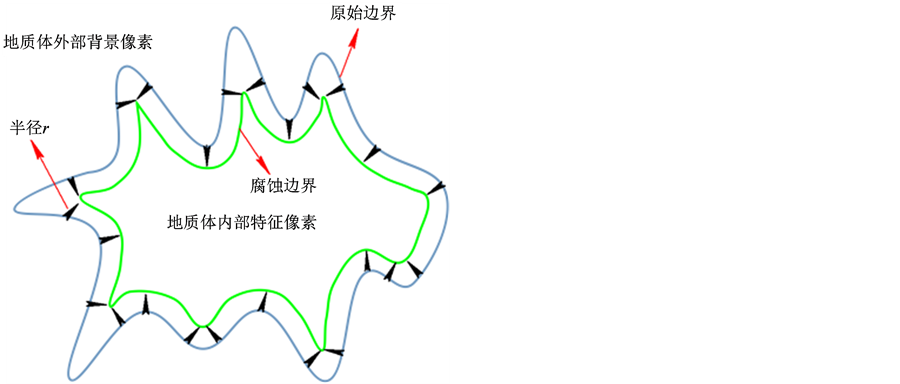
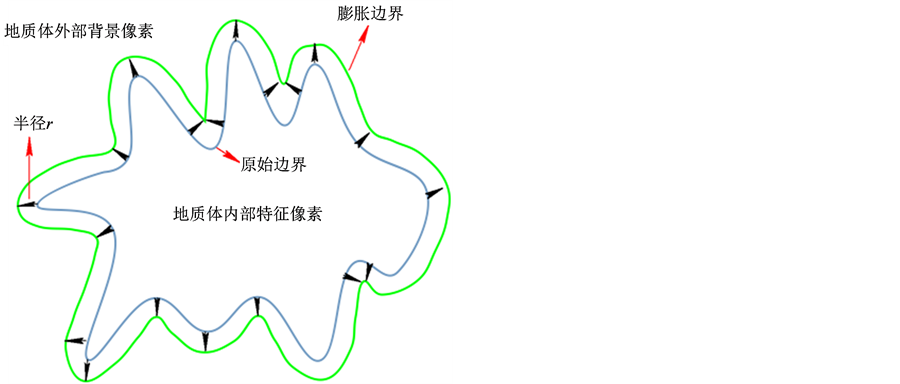
对欧式距离变换生成的距离场分析可知,在正欧式距离场中,岩体部分距离值为0,其余部分都被赋予了一定意义的距离向量,根据该位置体元距地质体表面的远近,由距离向量计算得到的距离值也不尽相同。因此,从正距离场中提取小于球体半径范围内的体元即可构成采用球形结构元素膨胀运算得到的结果,同样,从负距离场中提取大于球体半径范围内的体元即可构成采用球形结构元素腐蚀运算得到的结果(图5)。
为了更好地说明基于欧式距离变换的腐蚀与膨胀运算过程,使用A表示三维二值图像表达的地质体,Eouter表示生成的岩体外部正欧式距离场,Einner表示岩体内部负欧式距离场,给定的球形结构元素半径为r,则
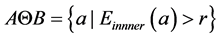 (8)
(8)
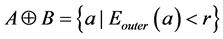 (9)
(9)
针对三维地质体对象,基于欧式距离变换的形态滤波可以采用类似数学形态学中级联滤波的方法,通过组合从正负欧式距离场一定半径范围内的体元提取过程,可以得到最终的滤波结果。从表达式(8)和(9)可以看出,基于欧式距离变换的形态滤波,每一次腐蚀与膨胀过程的工作重点在于欧式距离变换运算,与所选择的球形结构元素的规模基本无关,球形结构元素的半径只是用来规范选取的体元范围,保证最终两种方法的滤波结果一致。
4. 实验结果与分析
为了验证两种方法的正确性,以及对两种滤波方法的性能进行对比,本文选取安徽铜陵凤凰山矿田新屋里岩体作为目标,通过建立新屋里岩体的三维栅格模型,即三维二值图像,可以发现新屋里岩体表面存在广泛的弯曲和凹凸起伏现象(图6),选择该岩体进行形态滤波,可以很清晰地看出滤波效果,从而验证本文滤波方法的正确性。
分别采用10,20,40,80 m四种直径规模下的球形结构元素对新屋里岩体进行形态滤波,提取得到的岩体趋势形态见图7,从图中可以看出,随着结构元素的规模逐渐增大,滤波得到的岩体趋势形态越显光滑,充分展示了本文所实现的两种滤波方法的正确性。
经过验证,两种滤波方法得到的滤波效果图完全一致,表明两种滤波方法都可以得到正确的滤波结果。从理论时间复杂度考虑,若地质体的规模为N,球形结构元素直径为D,那么,基于数学形态学的腐蚀或膨胀运算,时间复杂度为O (N × D3),而采用基于欧式距离变换的腐蚀或膨胀运算,相应的时间复
 (a) 腐蚀运算 (b) 膨胀运算
(a) 腐蚀运算 (b) 膨胀运算
Figure 5. Erosion and dilation based on Euclidean distance transform
图5. 基于欧式距离变换的腐蚀与膨胀
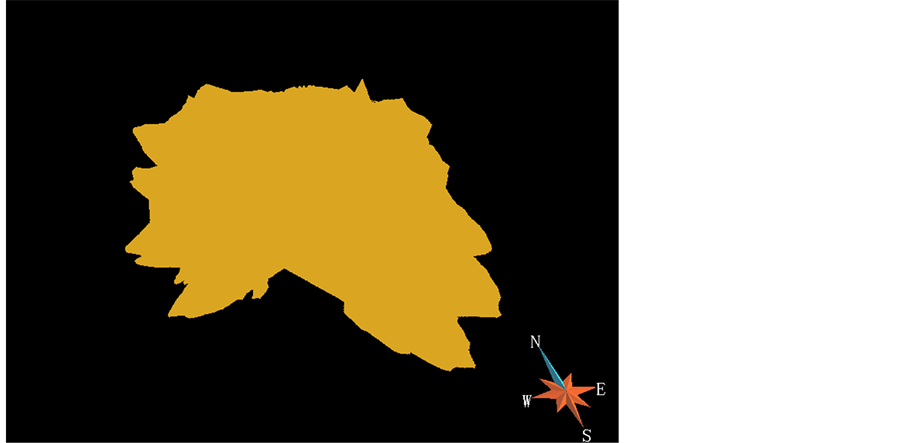
Figure 6. Original shape model of rock
图6. 地质体原始模型
杂度降为O (N)。因此,基于欧式距离变换的形态滤波似乎更满足大规模球形结构元素的滤波要求。为了验证这一结论,选择对两种滤波方法在不同规模球形结构元素下的运算时间进行统计实验。本次实验的计算平台为MS Windows 7系统,Intel corei5 2.3G和4GB内存的计算机,新屋里岩体的三维二值图像大小为880 × 1080 × 330。
从表1可以看出,两种形态滤波方法运算时间随着球体直径的增加而表现的截然不同,其中,基于数学形态学的形态滤波方法,其运算时间随着球体直径的增加而增长明显,且到了80 m直径规模的球形结构元素下,已经变得无法接受,而基于欧式距离变换的形态滤波方法,运算时间基本持平,与滤波球体直径几乎没有相关关系。这也验证了上述关于两种算法的理论时间复杂度分析。基于这些表现,我们认为,基于欧式距离变换的形态滤波总体性能要优于基于数学形态学的形态滤波方法,尤其是在需要使

 (a) 直径为10 m的球形结构元素滤波效果(b) 直径为20 m的球形结构元素滤波效果
(a) 直径为10 m的球形结构元素滤波效果(b) 直径为20 m的球形结构元素滤波效果
 (c) 直径为40 m的球形结构元素滤波效果(d) 直径为80 m的球形结构元素滤波效果
(c) 直径为40 m的球形结构元素滤波效果(d) 直径为80 m的球形结构元素滤波效果
Figure 7. Morphological filtering effects under different diameters
图7. 不同直径规模下的滤波效果图
Table 1. Computational times of two 3D morphological filtering methods under different diameters (time unit: s)
表1. 不同直径规模的球形结构元素下两种滤波方法运算时间(时间单位为s)
直径为10 m表示球形结构元素大小为10 × 10 × 10,依次类推
用大规模的球形结构元素时,这种优越性表现的更为明显。基于欧式距离变换的形态滤波方法,其运算时间主要来自于欧式距离变换的时间,针对本文的三维地质体对象,时间基本维持在2200秒左右,相对于本文后续计算的在直径为5 m的球形结构元素情况下,基于数学形态学的形态滤波时间为400秒左右,因此,在球形结构元素直径较小的情况下,选择基于数学形态学的形态滤波优势较为明显。
5. 结束语
本文以安徽铜陵凤凰山矿田新屋里岩体为背景,在选用球形结构元素的前提下,运用基于数学形态学与基于欧式距离变换的两种三维形态滤波方法对地质体二值图像展开滤波运算,并统计不同直径规模球形结构元素下的运算时间,分析得出如下结论:
1) 两种滤波方法得到的滤波结果完全一致;
2) 在针对大规模球形结构元素的形态滤波中,基于欧式距离变换的滤波方法运算时间明显少于基于数学形态学的方法,且随着滤波球体直径的增加,这种差别表现地越明显。
针对本文研究所选用的地质体对象,通过细致分析,我们发现滤波球体直径大于10 m的情况下,采用基于欧式距离变换的方法非常有效,其运算时间不会随着球形结构元素规模的增加而增加;滤波球体直径小于10 m时,可考虑直接采用基于数学形态学的方法,因为该方法运算时间是与球体规模紧密相关的,在球体直径较小时,采用该方法更为有效。本文下一步的工作将考虑对基于数学形态学的滤波方法设计出相应的并行算法,并予以实现,通过多处理器性能来改善串行计算时间上的局限性。
基金项目
国家自然科学基金资助项目(41472301, 41172297)。
文章引用
张 彬,毛先成. 基于球形结构元素的两种三维形态滤波方法
Two 3D Morphological Filtering Methods Based on Sphere Structuring Element[J]. 图像与信号处理, 2016, 05(01): 33-42. http://dx.doi.org/10.12677/JISP.2016.51005
参考文献 (References)
- 1. Serra, J. (1982) Image Analysis and Mathematical Morphology. Academic Press, London.
- 2. Serra, J. (1986) Introduction to Mathematical Morphology. Computer Vision Graphics & Image Processing, 35, 283- 305. http://dx.doi.org/10.1016/0734-189X(86)90002-2
- 3. 王树文, 闫成新, 张天序, 等. 数学形态学在图像处理中的应用[J]. 计算机工程与应用, 2004, 32(1): 89-92.
- 4. 刘志敏, 杨杰. 基于数学形态学的图像形态滤波[J]. 红外与激光工程, 1999, 28(4): 10-15.
- 5. 汤井田, 李晋, 肖晓, 等. 基于数学形态滤波的大地电磁强干扰分离方法[J]. 中南大学学报(自然科学版), 2012, 43(6): 2216-2221.
- 6. 陈汗青, 万艳玲, 王国刚. 数字图像处理技术研究进展[J]. 工业控制计算机, 2013, 26(1): 72-74.
- 7. 林雯. 基于三维图像处理的港口物流集装箱吊装真实化模拟[J]. 物流技术, 2014, 33(6): 360-362.
- 8. Danielsson, P.E. (1980) Euclidean Distance Mapping. Computer Graphics and Image Processing, 14, 227-248. http://dx.doi.org/10.1016/0146-664X(80)90054-4
- 9. 蔡建军, 孔令富, 李海涛. 基于欧式距离变换的人体2D关节点标定[J]. 计算机仿真, 2012, 29(7): 243-246.
- 10. 解聪, 雷辉,徐星, 等. 基于并行欧式距离变换的三维障碍距离场计算[J]. 浙江大学学报(工学版), 2014, 48(2): 360-367.
- 11. 毛先成, 唐艳华, 赖建清, 等. 凤凰山矿田成矿地质体三维结构与控矿地质因素分析[J]. 地质学报, 2011, 85(9): 1508-1518.
- 12. 姜红军, 冯立昇, 平子良. 数学形态学早期思想的形成[J]. 西北大学学报(自然科学版), 2011, 41(6): 1112-1116.
- 13. 崔屹. 图象处理与分析——数学形态学方法及应用[M]. 北京: 科学出版社, 2000.
- 14. 陈崚. 完全欧几里得距离变换的最优算法[J]. 计算机学报, 1995, 18(8): 612-616.
- 15. 任勇勇, 潘泉, 张绍武, 等. 基于围线分层扫描的完全欧式距离变换算法[J]. 中国图像图形学报, 2011, 16(1): 33- 36.
- 16. 崔峰, 汪雪林, 彭思龙. 近似欧式距离变换的一种并行算法[J]. 中国图像图形学报, 2004, 9(6): 694-698.
- 17. 蔺宏伟, 王国瑾. 三维带符号的欧式距离变换及其应用[J]. 计算机学报, 2003, 26(12): 1646-1651.
*通讯作者。
