Journal of Image and Signal Processing
Vol.
10
No.
01
(
2021
), Article ID:
40078
,
12
pages
10.12677/JISP.2021.101005
基于分式惩罚函数的块稀疏信号重构
陈鸽
西南大学数学与统计学院,重庆

收稿日期:2020年12月28日;录用日期:2021年1月20日;发布日期:2021年1月28日

摘要
压缩感知作为一种新颖的信号处理理论突破了传统的采样定理,以信号的稀疏性和可压缩性为基础,实现对信号的高效获取和精确重构,在各个领域均有实际意义。本文以压缩感知为基础,研究基于分式惩罚函数的块稀疏信号重构问题,即以分式函数 代替 ,将 范数优化问题转化为FPB优化问题,同时给出了FPB-DC算法,并用ADMM算法解决FPB-DC算法遗留下来的凸子问题。另外我们进行了数值仿真模拟实验,在信噪比、重构准确率等方面与Lasso-ADMM算法、FP-DC算法做了相关比较,实验表明:成功率随稀疏度增加时,新算法的成功率显著高于其余两种算法;SNR在随稀疏度增加时,整体上FPB-DC算法的SNR高于其余两种算法;FPB-DC算法在重构性能上确实具有一定优势。
关键词
压缩感知,信号重构,FPB-DC算法,分式惩罚函数,块稀疏

Block Sparse Signal Reconstruction Based on Fractional Penalty Function
Ge Chen
School of Mathematics and Statistics, Southwest University, Chongqing
Received: Dec. 28th, 2020; accepted: Jan. 20th, 2021; published: Jan. 28th, 2021

ABSTRACT
As a novel signal processing theory, compressed sensing breaks through the traditional sampling theorem. Based on the sparsity and compressibility of the signal, it can achieve efficient acquisition and accurate reconstruction of the signal, which has practical significance in various fields. Based on compressed sensing, this paper studies the problem of block sparse signal reconstruction based on fractional penalty function. The fractional function is used instead of , the norm optimization problem is transformed into FPB optimization problem, and the FPB-DC algorithm is given. The algorithm uses the ADMM algorithm to solve the convex problem left over from the FPB-DC algorithm. In addition, we have carried out numerical simulation experiments, and compared with Lasso-ADMM and FP-DC algorithm in terms of signal-to-noise ratio and reconstruction accuracy. The results show that the success rate of the new algorithm is significantly higher than that of the other two algorithms when the sparsity increases; with the increase of sparsity, the SNR of FPB-DC algorithm is higher than that of the other two algorithms on the whole; FPB-DC algorithm does have some advantages in reconstruction performance.
Keywords:Compressed Sensing, Signal Recovery, FPB-DC Algorithm, Fractional Penalty Function, Block Sparsity

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着科技的不断进步及大数据时代的来临,人们对信息的传输、处理、储存要求日益提高,如何收集和分析海量的数据以获取有效信息显得极为重要。1928年,由美国物理学家H.奈奎斯特提出的奈奎斯特采样定理(Nyquist采样定理) [1],以大于信号中最高频率的2倍的采样频率,使得采样之后的数字信号完整地保留原始信号中的信息,但奈奎斯特采样频率会受物理条件及其硬件设施的限制。
2006年,由美国科学院院士D. Donoho、E. Candes及华裔科学家T. Tao等人提出了的压缩感知 压缩传感,Compressive Sensing)理论 [2] [3] 与Nyquist理论不同,它突破了Nyquist理论对信号采样的限制,该理论的原理是只需信号在某个领域上是稀疏的或可压缩的,就可以用一个与变换基不相关的观测矩阵将变换后的高维稀疏信号投影到低维空间上,然后通过求解优化问题将少量的投影信息高精度地恢复成原始信号。其过程是将压缩与采样合并进行,实现了信号的高效采集,使得高速、高质量的信息传输成为可能。该理论一经提出便引起学者广泛研究,目前已在磁共振成像(MRI)、天文学、线性编码、模式识别、地质勘探、生物传感、CT断层扫描等领域得到广泛应用。
CS理论的关键环节是信号重构,且建立在数据稀疏特征上,其目的是从非自适应的低维数据准确有效地重构原始高维数据。信号重构过程中最直接方法是将其转化为一个极小 范数下的最优化问题,但这是一个NP难问题(NP指非确定性多项式),理论上很难求解。在实际中,一种是去寻找其近似求解方法,经典算法有贪婪算法和硬阈值算法 [4] [5] [6],这两类算法结构简单,计算速度快,但是其准确率不高,容易受到噪声干扰。另一种是寻找新的模型替代 范数,再求解,首先由Candes和Tao等人提出 [7] 范数替代 范数求解 [8] [9],尽管 范数是 范数在逼近论角度看来是最凸的逼近,但该方法不能得到充分稀疏的解。而文献 [10] 中提出了用一个分式函数的极限来近似 范数,可以得到更加精确的结果。
然而随着逐渐深入的研究,发现一些信号数据是以块的形式聚集在一起,有着特殊的结构化稀疏特征,即块稀疏性,表现最为明显是彩色图像处理应用 [11],以上重构方法并不能有效应对这些数据。因此,研究块稀疏数据相关的理论和算法在实际应用中有着十分重要的科学意义。Eldar等人 [12] 针对这一问题进行研究,并提出 问题,即文章中问题(3),针对这一问题的求解,可以用BCD算法 [13] 以及ADMM [14] 等方法。
受文献 [10] 中方法的启发,用基于块的分式函数重新建模问题(9),将 优化问题转化为FPB优化问题,同时探讨了关于该问题的算法,给出了FPB-DC算法,并用ADMM算法解决FPB-DC算法遗留下来的凸子问题。另外我们进行了数值仿真模拟实验,在信噪比、重构准确率等方面与Lasso-ADMM算法、FP-DC算法做了相关比较,实验表明:成功率随稀疏度增加时,新算法的成功率显著高于其余两种算法;SNR在随稀疏度增加时,整体上FPB-DC算法的 高于其余两种算法;FPB-DC算法在重构性能上确实具有一定优势。
2. 压缩感知及块压缩感知理论
2.1. 压缩感知理论
z是采样得到的信号,经过正交变换或小波变换后的系数是稀疏的,即 ,其中 为信号z的系数稀疏表示,且 ,k为稀疏度, 表示x中非0元素的个数。测量信号y在无噪的情况下可以表示为 ,, 为基函数字典,测量矩阵 ,一般令 , 且被称为感知矩阵(传感矩阵),信号重构问题其实就是稀疏信号的恢复过程,类似于一个解码的过程,通过y反求x。可以将其转化为极小 范数 [15] 的求解问题(1)。
(1)
还可以将上述极小化 范数问题(1)转化为如下无约束极小化 正则化问题。
(2)
由于 是不连续函数,不满足范数的齐次性,即 ,因此该问题是一个NP难问题,会有无穷多个解;为了克服这个问题,经过一系列的探索,找到了一些求解该问题最优解的方法,比如最凸优化算法、贪婪算法、正交匹配追踪法(OMP) [16]、迭代阈值法 [6] 等。
2.2. 块压缩感知理论
自从压缩感知技术被提出后,随着广泛的关注和深入的研究,发现一些信号数据是以块的形式聚集在一起,和传统的稀疏信号不同,有着特殊的结构化稀疏特征,即块稀疏性,在图像和视频中广泛存在。
2.2.1. 块稀疏概念
从数学的角度来说,块稀疏就是信号中的非0元素以块的形式出现,给定一个分块 ,任意向量 都可以表示为
如果向量x至多有k个非0块,就称该向量为块k-稀疏信号,记为 。其中
表示指示函数。
同时,测量矩阵B可以表示为
则从 中重构稀疏信号的问题转化为 的块稀疏信号重构问题。
2.2.2. 块压缩感知重构理论
上述块稀疏信号我们不能用传统的压缩感知方法来处理,同时深层的稀疏结构性质又不能被忽视。因此,我们需要改进原始的极小化 范数方法,文献 [17] 中使用极小化 范数方法和极小化 ( )范数方法代替原来的 范数,这样做可以使块的结构特征得以体现,还能使原来的NP-hard问题变得简单,我们称这种方法为极小化 方法,有学者 [17] 提出如下的极小化 问题
(3)
其中 ,在这种结构中,信号恢复的方法是建立在 范数( 范数)上的,但是还存在一些问题,比如数据之间还存在很大的冗余性,并且没有去除,这样最终会降低精确重构效果。我们发现在文献 [10] [18] 中提出了用分式惩罚函数替代不连续函数 ,可以提高信号重构的精确度。
3. FP0优化问题理论分析及算法
3.1. 分式惩罚函数及FP0优化问题
由于问题(1)的 范数优化问题是NP难问题,很难得到解,因此我们用分式函数 替代 ,精简计算复杂度,将 范数优化问题(1)转化为基于分式惩罚函数的 范数优化问题,即下面式子所表示的FP0优化问题
(4)
其中 。可以将其等价转化为无约束优化问题,
( ) (5)
3.2. FP0优化问题最优解的性质
在文献 [10] [18] 中提出了FP0化问题的局部最优解 的稀疏度最大,不会超过rank(B);FP0优化问题的局部最优解的个数是有限的,严格证明了对于向量 ,,以及 如果满足
1) 矩阵 非奇异,i.e.矩阵 的列线性无关;
2) ;
3) 向量 是不动点, ,其中 ;
4) ,其中 表示给定对称矩阵的最小特征值
那么向量 是无约束(FP0)优化问题的部分最优解。特别的是,当(4)的不等式严格成立时,则向量 是无约束(FP0)优化问题的严格局部最优解。
3.3. FP0优化问题与L0-范数优化问题的等价性分析
对于 范数优化问题,我们利用分式函数 替代不连续函数 ,最终将 范数优化问题转化为FP0优化问题.但我们必须保证在一定条件下,使(FP0)优化问题的最优解( )仍然是原问题 范数优化问题的最优解( ),在文献 [10] 中已经分别给出了基于RIP性质条件下的FP0优化问题与 范数优化问题是等价的这一结论。
首先,测量矩阵B需要满足一定条件来保证感知矩阵Φ满足RIP性质,即找到一个适当大的L,使 始终成立。再者,需要满足基于分式函数的稀疏优化问题的稀疏解的精确恢复条件,即对于给定的测量矩阵D,找到 ,使得
(6)
成立,那么存在 ,对于任意的 ,,使( )优化问题的最优解 唯一且等于 范数优化问题的最优解 。
4. 基于分式惩罚函数的块稀疏信号重构FPB-DC算法
前面介绍块稀疏信号恢复的方法可以建立在 范数上,但是由于数据之间还存在很大的冗余性没有去除这一问题,就会降低我们需要精确重构的测量次数。而FP0优化问题能够很好的代替不连续函数 ,并且得到无约束FP0优化问题的最优解是局部最优解这一结论。因此,我们考虑将分式惩罚函数及块稀疏性进行结合,将问题(3)式进行优化,本文将研究基于分式惩罚函数的块稀疏信号重构,即FPB
优化问题。我们利用块分式函数 代替 范数 ,将 范数优化问题转化为(FPB)
优化问题,对信号的稀疏性进行正则化约束。最终,对DC算法(差分凸函数算法)进行改进,提出新的算法即FPB-DC算法,并且采用ADMM算法解决其凸 正则化子问题。
考虑以下无约束FPB优化问题
(7)
其中 。
4.1. DC算法
DC算法 [19] (差分凸优化算法)充分利用了凸分析方法可以将非凸优化问题转化为凸优化问题,而且该算法的特点是收敛速度快;在此之前先介绍一下DC函数。
DC函数定义如下:
若D是 的一个凸子集,对于实值函数 : ,如果存在两个下半连
续凸函数 , : ,并且满足 ,则称函数 在D上是DC的。若 ,就称 为DC函数。 , 叫做DC直流分解,是关于 的分量。无约束DC规划问题如以下表达式
(8)
利用函数 在当前迭代点 处的仿映射来近似代替函数L,即
DC算法中包含两个数列 ,, 是 在 处的次梯度,有以下迭代计算:
为 的最小解,证明如下:
特别的是 ,
因此该迭代产生了一个单调递减序列 ,并且它的收敛性证明了 是有界的。
4.2. FPB-DC算法
考虑(7)式无约束FPB优化问题
其中 。我们可以进行DC分解,令 ,,即
因为 是可微的, ,,当 时, ,又因为 ,所以
因此有如下的迭代结果:
关于上式的终止条件是 当 ,即对于给定的 ,有 。
每迭代一次,我们需要求解一次凸 正则化子问题,即
(10)
事实上,该问题是一个无约束 范数优化问题,在本文中我们用ADMM算法求解。
4.3. ADMM算法解决凸子问题
在DC迭代中,需要解决以下形式的凸子问题
(11)
,是一个常数向量。关于上式问题可以通过交替方向乘子法(ADMM),ADMM算法既有乘子法的强收敛性,又有对偶上升法的分解性。它利用一种交替求解的想法,将大的全局问题分解为容易求解的、小的局部子问题,再通过协调子问题的解来得到全局问题的最优解。这是一种多用途的算法,在文献 [20] 中首次引入,将(11)式重新定义为下面式子
(12)
形成拉格朗日函数:
其中y是拉格朗日乘数, 是惩罚参数,ADMM迭代步骤如下:
在x的更新步骤中, ,,则x的更新结果如下:
在c的更新步骤中,我们需要定义一个软阈值函数
则c的更新结果如下
ADMM算法的停止条件是:
,
,
其中 , 是原始残差和对偶残差,特别地,在第l次迭代中, 是绝对容错度, 是相对容错度。
5. 数值仿真实验与分析
为了进一步的阐述并且证明以上所提出算法的有效性,我们执行了相关的数值实验,将该算法应用到一般的压缩感知问题中去,即通过已知获得的随机信号观测变量准确重构出原稀疏信号变量。实验中,通过计算机随机模拟出一组长度为n且稀疏度为k的随机信号x,并且我们还要求该随机信号的非零元素位置都是随机选择的,都服从标准正态分布,并对该随机信号正规化、单位化处理。同时产生维度为 的采样矩阵B,其中的元素都独立服从高斯分布。实验在CPU为2.60GHz AMD的笔记本电脑中用MATLAB(R2016b)软件操作实现的。
5.1. FPB-DC算法的信号恢复
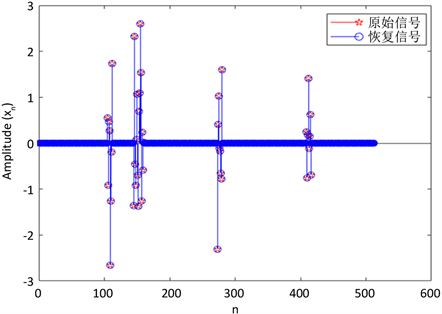
Figure 1. Reconstruction result of original signal
图1. 原始信号重构结果
在数值实验中,选取满足 高斯独立分布的 维矩阵B来恢复块k-稀疏向量 ,这样的矩阵在RIP性质上,满足的概率很大。采用的是维度为 256 × 512的采样矩阵B,并设定信号长度为256,块数s = 64,稀疏度为 的原始信号,我们令参数 ,,参数 ,执行FPB-DC算法,结果如图1所示。
从上图我们可以看出重构信号(蓝色)能够完全覆盖原始信号(红色),说明了新提出的FPB-DC算法重构性能比较好。
5.2. 算法比较
为了研究各算法之间的差异与关系,证明提出的新算法(FPB-DC算法)在信号重构上确实有一定的进步,我们将该算法与Lasso-ADMM、FP-DC算法进行比较,因为FPB-DC算法与Lasso-ADMM、FP-DC算法都是将ADMM与其他高精度算法结合起来解决优化问题,从而得到最优解。
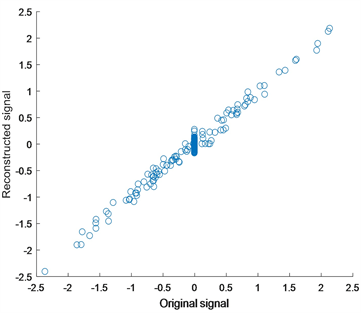
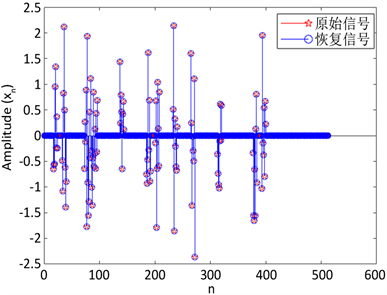
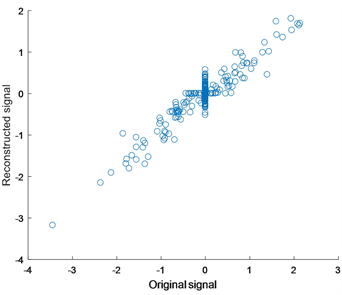
我们得到图2的实验结果,它们分别展现了FPB-DC算法与Lasso-ADMM、FP-DC算法的重构结果及对应的重构信号 与原始信号x元素之间一一对应的散点图,其中散点图对应的点与斜率为1的直线拟合得越好,说明我们重构的信号与原始信号越接近。
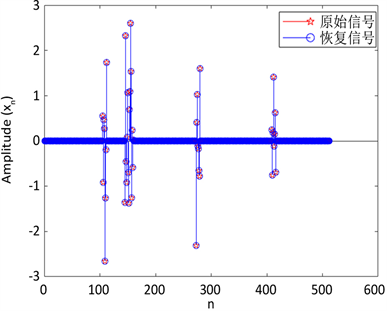 (a)
(a)
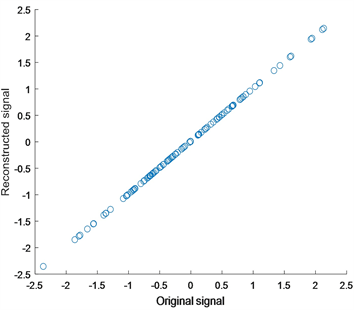 (b)
(b)
 (c)
(c)
 (d)
(d)
 (e)
(e)
 (f)
(f)
Figure 2. Reconstruction performance comparison of each algorithm
图2. 各算法重构性能比较
在图2中,图a、c、e分别为FPB-DC、Lasso-ADMM、MP-DC算法的重构结果,图 分别为原始信号与FPB-DC、Lasso-ADMM、MP-DC算法下重构信号的散点图;从图中反映的情况来看,我们提出的FPB-DC算法散点图拟合的更好,展现出更高质量的重构性能,从图中反映的情况来看,我们提出的FPB-DC算法散点图拟合的更好,展现出更高质量的重构性能,并且FPB-DC算法和FP-DC、Lasso-ADMM
算法下的相对误差即 ,分别为0.007331,0.05174,0.034692,因此FPB-DC算法的重构性能较好。
5.2.1. 信噪比上的对比
在接下来,我们利用信噪比SNR(信号与噪声的比例)对其进一步测量,具体公式如下所示。SNR值越高则算法的重构性能越好。我们考虑重构信号的信噪比随着信号稀疏度k的增加所呈现的变化趋势。

Figure 3. The change trend of SNR of each algorithm with the increase of sparsity k
图3. 各算法对应的信噪比随稀疏度k的增加所呈现的变化趋势
在该实验中,采用的是维度为256 × 512的采样矩阵B,块数为64,原始信号x的稀疏度k设置为0~20;其余参数设定与前面一致,我们每一个实验结果都采用随即模拟实验100次的结果所取的平均值。
所有的测试结果在图3中展示出来,从图的整体曲线趋势来看,当稀疏度 时,FPB-DC算法的SNR = 38,FP-DC和Lasso-ADMM算法的SNR一样,即SNR = 20,FPB-DC算法的SNR要高一些;而在 时,FPB-DC算法和和Lasso-ADMM算法的SNR一样,即SNR = 7,FP-DC算法的SNR = 4;因此整体上来看FPB-DC算法比FP-DC和Lasso-ADMM算法在信号重构方面更具有优势和效率,但在图3中当稀疏度k从15逐渐增大时,所呈现的FPB-DC算法重构性能优于FP-DC和Lasso-ADMM算法的效果并不怎么显著,其原因可能是该实验中对应不同稀疏度的信号重构参数的选择欠妥或者是算法本身的局限性,但从总体上来看新算法的信噪比(SNR)相对要高一些,即说明新算法的重构性能是有所改善优化的。
5.2.2. 重构准确率上的对比
为了再次证明提出的新算法(FPB-DC算法)在信号重构上确实有一定的进步,我们记录了随着原始信号稀疏水平k的变化,不同算法获得的重构信号的准确率大小。本次试验中的成功率定义为: 。在本次实验中,依旧采用维度为256 × 512的采样矩阵B来进行测试参数设定与前面保持一致,每个算法在不同的稀疏水平下都是随机重复执行100次。

Figure 4. Signal reconstruction accuracy of each algorithm under different original signal sparsity levels
图4. 在不同的原信号稀疏水平下各算法对应的信号重构准确率
结果如图4所示,我们将原信号的稀疏水平设置为5∼20的区间内,从上图我们可以看出:当稀疏度 时,FPB-DC算法的成功率为90%,Lasso-ADMM算法的成功率为70%,FP-DC算法的成功率为18%,因此在 时FPB-DC算法比FP-DC、Lasso-ADMM算法的信号恢复成功率都高;当稀疏度 时,FP-DC、Lasso-ADMM算法的成功率为0,FPB-DC算法的成功率为10%,而在 时,FPB-DC算法的成功率才为0,随着稀疏度的增加,FP-DC、Lasso-ADMM算法的成功率先趋于0,这也说明了基于分式惩罚函数的块稀疏算法(FPB-DC)的重构优越性。
6. 总结
本篇文章中,我们提出了基于分式惩罚函数的块稀疏信号恢复问题,对于(5)式,将块稀疏信号恢复
的方法建立在 范数上,我们用分式函数 代替 范数 ,对信号的稀疏性进行正
则化约束,即得到FPB优化问题,并针对该问题,我们提出FPB-DC算法,从数值实验结果中信号恢复的信噪比大小和成功率来看,实现了算法重构性能和收敛速度的改善。另外,我们还发现FPB-DC算法在准确重构原信号时所需的样本采样量明显低于FP-DC、Lasso-ADMM算法,为数据信号的采样缓解了压力。但是发现仍然有待解决的问题:本文的算法理论分析是以无噪声信号处理为基础的,没有考虑有噪声信号的重构理论。该问题也需要进一步研究。
文章引用
陈 鸽. 基于分式惩罚函数的块稀疏信号重构
Block Sparse Signal Reconstruction Based on Fractional Penalty Function[J]. 图像与信号处理, 2021, 10(01): 36-47. https://doi.org/10.12677/JISP.2021.101005
参考文献
- 1. Nyquist, H. (1928) Certain Topics in Telegraph Transmission Theory. Transactions of the American Institute of Electrical Engineers, 47, 617-644.
https://doi.org/10.1109/T-AIEE.1928.5055024 - 2. Donoho, D.L. (2006) Compressed Sensing. IEEE Transactions on Information Theory, 52, 1289-1306.
https://doi.org/10.1109/TIT.2006.871582 - 3. Candes, E.J., Romberg, J.K. and Tao, T. (2006) Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Transactions on Information Theory, 52, 489-509.
https://doi.org/10.1109/TIT.2005.862083 - 4. Blumensath, T. and Davies, M.E. (2009) Iterative Hard Thresholding for Compressed Sensing. Applied and Computational Harmonic Analysis, 27, 265-274.
https://doi.org/10.1016/j.acha.2009.04.002 - 5. Blumensath, T. and Davies, M.E. (2010) Normalized Iterative Hard Thresholding: Guaranteed Stability and Performance. IEEE Journal of Selected Topics in Signal Processing, 4, 298-309.
https://doi.org/10.1109/JSTSP.2010.2042411 - 6. 杨海蓉, 方红, 张成, 等. 基于回溯的迭代硬阈值算法[J]. 自动化学报, 2011, 37(3): 276-282.
- 7. 蔡剑. DC规划的分支算法[J]. 科学技术与工程, 2009, 9(9): 2271-2286
- 8. Candes, E.J. and Tao, T. (2005) Decoding by Linear Programming. IEEE Transactions on Information Theory, 51, 4203-4215.
https://doi.org/10.1109/TIT.2005.858979 - 9. Donoho, D.L. (2006) For Most Large Under-Determined Systems of Linear Equations the Minimal l1-Norm Solutionis Also the Sparsest Solution. Communications on Pure and Applied Mathematics, 59, 796-825.
https://doi.org/10.1002/cpa.20132 - 10. 崔安刚. 基于分式函数的l0-范数优化的理论与DC算法研究[D]: [硕士学位论文]. 西安: 西安工程大学, 2016: 9-36.
- 11. Majumdar, A. and Ward, R. (2010) Compressed Sensing of Color Images. Signal Processing, 90, 3122-3127.
https://doi.org/10.1016/j.sigpro.2010.05.016 - 12. Eldar, Y.C. and Mishali, M. (2009) Robust Recovery of Signals from a Structured Union of Subspaces. IEEE Transactions on Information Theory, 55, 5302-5316.
https://doi.org/10.1109/TIT.2009.2030471 - 13. Qin, Z.W., Scheinberg, K. and Goldfarb, D. (2013) Efficient Block-Coordinate Descent Algorithms for the Group Lasso. Mathematical Programming Computation, 5, 143-169.
https://doi.org/10.1007/s12532-013-0051-x - 14. Boyd, S., Parikh, N., Chu, E., et al. (2011) Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends in Machine Learning, 3, 1-122.
https://doi.org/10.1561/2200000016 - 15. Mohimani, H., Babaie, Z.M. and Jutten, C. (2009) A Fast Approach for Overcomplete Sparse Decomposition Based on Smoothed l0-Norm. IEEE Transactions on Signal Processing, 57, 286-302.
https://doi.org/10.1109/TSP.2008.2007606 - 16. Tropp, J. and Gilbert, A. (2007) Signal Recovery from Random Measurements via Orthogonal Matching Pursuit. IEEE Transactions on Information Theory, 53, 4655-4666.
https://doi.org/10.1109/TIT.2007.909108 - 17. 王文东. 块压缩感知的l2/l1(0 < q≤1)极小化算法研究[D]: [硕士学位论文]. 重庆: 西南大学, 2014: 12-24.
- 18. Li, H.Y., Zhang, Q., Cui, A.G. and Peng, J.G. (2017) Minimization of Fraction Penalty in Compressed Sensing. IEEE Transactions on Neural Networks and Learning Systems, 17, 9-16.
- 19. Baraniuk, R.G. (2007) Compressed Sensing. IEEE Signal Processing Magazine, 24, 118-121.
https://doi.org/10.1109/MSP.2007.4286571 - 20. 戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报, 2011, 34(3): 401-425.