Software Engineering and Applications
Vol.3 No.03(2014), Article
ID:13709,7
pages
DOI:10.12677/SEA.2014.33010
Personalized Mechanism of Randomization Based on Multi-Agent Technology
School of Economics and Management, Beijing Jiaotong University, Beijing
Email: 11243022@bjtu.edu.cn, 13120630@bjtu.edu.cn
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Apr. 8th, 2014; revised: May 11th, 2014; accepted: May 20th, 2014
ABSTRACT
Due to the homogeneity of cellular and the simplicity of algorithm, traditional CA modeling use common randomization probability to describe behaviors of velocity randomization, which is difficult to reflect the factors on velocity randomization completely. In this paper, we decompose factors of velocity randomization in “ideal model” and “participant characteristic model”, integrate those factors and create the mechanism of personalized randomization in “Multi-Agent interaction model”. Integrity of the simulation on behaviors of velocity randomization is enhanced effectively by introducing the mechanism we create. For individual traffic participants, behaviors of velocity randomization are no longer explained by a simple, abstract randomization probability, but decided by its unique personalized velocity randomization mechanism. While for the entire transportation system, differences between the individual participants lead to different personalized velocity randomization mechanism.
Keywords:Multi-Agent, Velocity Randomization, Personalization, Factor Decomposition, Factor Integration

基于多Agent技术的个性化随机慢化机制研究
于黎明,乔 欢
北京交通大学,经济管理学院,北京
Email: 11243022@bjtu.edu.cn, 13120630@bjtu.edu.cn
收稿日期:2014年4月8日;修回日期:2014年5月11日;录用日期:2014年5月20日

摘 要
元胞个体的同质化与单一性,以及模型演化算法的简单性,导致传统元胞自动机(CA)模型忽略参与者个体差异,使用共性化随机慢化概率统一表述随机慢化行为,难以完整反映随机慢化行为的影响因素。本文通过多层次Agent模型中的理想模型和参与者特征模型对随机慢化行为影响因素进行分解,进而通过多Agent协同模型进行随机慢化行为影响因素集成,形成个性化随机慢化机制。引入该机制后,对于个体交通参与者,其随机慢化行为不再由简单、抽象的随机慢化概率涵盖,而是由其独有的个性化的随机慢化机制决定;而对于整个交通系统,由于参与者个体之间的差异性,导致不同参与者随机慢化的机制体现出个性化差异,系统对于随机慢化行为模拟的完整性得到有效增强。
关键词
多Agent,随机慢化,个性化,因素分解,因素集成

1. 引言
在交通社会系统中,存在诸多引发司机采取减速行为的因素,其中既包括交通工程因素,也包括社会文化因素。由于这些因素难以穷尽,而且不同因素之间产生许多组合效果,因此国内外学者普遍将司机因各种不确定因素而采取的减速行为定义为随机慢化行为。
对于随机慢化行为的处理,传统基于CA的交通建模一般通过规定“随机慢化概率”从而实现司机的随机慢化行为。1992年Nagel和Schreckenberg提出了NaSch模型,最早在车辆运动中引入了随机慢化的可能性,以区间[0,1]内的一个恒定常数p作为随机慢化概率,来反映驾驶员不同的行为习惯及各种不确定因素造成的车辆减速过程。为了更好的反映随机慢化的影响因素,国内外学者提出了许多改进模型,调整随机慢化规则中行驶车辆的减速概率。例如:
Barlovic等人提出的VDR模型[1] 是NaSch模型的一个简单扩展模型,模型中车辆在随机慢化过程中的减速概率不再是区间[0,1]内的恒定常数,而是车辆速度的函数,也即p = p(v)。李晓白等人提出了一个能近似考虑前车速度效应(VE)的模型[2] ,加入前车速度的影响,在NaSch模型基础上对减速条件做了改进,模拟效果比NaSch模型更接近于实际情况。姜锐等人提出了由车辆停留时间确定随机慢化概率的交通流模型[3] ,李启朗等人则提出了基于车间距的交通流模型[4] 。而在近期的研究中,驾驶员特性的影响也引起了越来越多的关注。例如考虑驾驶员安全驾驶需求的影响[5] ,考虑混合车辆之间的速度差异及驾驶员敏感程度的不同的影响[6] ,考虑驾驶员不确定性敏感预期行为的影响[7] ,考虑安全距离的影响[8] ,考虑驾驶员不同特性的影响[9] ,考虑司机的记忆效应和当前环境的影响[10] ,考虑驾驶员不同驾驶水平的影响[11] 等。
尽管随着研究的深入,国内外学者从不同角度对随机慢化概率做出完善,然而现有交通建模研究以随机慢化概率处理随机慢化行为的方法却存在以下几点缺陷:
其一,将越多导致司机随机慢化的因素引入随机慢化概率,则随机慢化概率的抽象简化程度就越高,也就越难完整反映所有因素,同时,数学建模难度也越大。
其二,对于不同类型的司机,可能造成其随机慢化行为的因素将随其参与者特征的变化而产生差异。随机慢化概率可以反映其中的共性因素,却难以反映其中的个性因素。
造成以上缺陷的主要原因是:传统CA模型中元胞的同质化与单一性,以及模型演化算法的简单性,导致建模过程中不得不忽略随机慢化规则中的参与者个体差异,使用共性化随机慢化概率的形式统一表述、抽象简化。
为解决以上问题,本文通过引入多层次Agent模型,将随机慢化行为的处理方法由共性化的随机慢化概率转化为个性化的随机慢化机制,从而有效增强交通模拟系统对于社会复杂性的描述:对于个体交通参与者,其随机慢化行为就不再由一个简单、抽象的随机慢化概率涵盖,而是由其独有的个性化的随机慢化机制决定;而对于整个交通系统,由于参与者个体之间的差异性,导致不同参与者随机慢化的机制也不尽相同,系统对于随机慢化行为模拟的完整性度得到有效增强。
全文共包括引言、结论在内的5个部分,其中第2部分将给出基于多层次Agent模型的随机慢化影响因素分解方法,各种随机慢化行为的影响因素将在理想模型和参与者特征模型中被分解,进而归为不同类型Agent的属性;第3部分将给出基于多Agent协同模型的随机慢化行为影响因素集成过程,主体参与者Agent感知其他Agent(如道路、其他参与者)属性,再由其知识库通过获取的Agent属性形成随机慢化行为的影响因素,进而结合自身参与者Agent属性,形成个性化的随机慢化机制;第4部分以黄灯困境为例,对随机慢化行为因素分解方法以及个性化随机慢化机制形成过程进行模拟实证。
2. 基于多层次Agent模型的随机慢化影响因素分解
随机慢化行为的影响因素主要包括交通工程因素以及社会心理因素两大类,为了完整体现这两类因素,需要对其进行分解,再将分解后的基本元素赋予各类Agent成为它们的属性。各类随机慢化影响因素经分解得到的基本元素的数量相对因素本身较少,因此这种处理方法可以确保因素描述的完整性。
多层次Agent模型包括“理想模型”、“参与者特征模型”以及“多Agent协同模型”三个层次。理想模型是基于交叉口设计规范与交通法规的抽象和简化,在理想模型中,整个交通系统像机器一样有序运行;在参与者特征模型中,通过引入基于计划行为理论的参与者Agent知识库系统对理想模型中的参与者Agent基本结构进行拓展,从而体现交通参与者复杂的交通行为和交通心理;本节进行重点介绍交通工程因素和社会心理因素被分解为基本元素并分别赋予理想模型和参与者模型中的各类Agent成为其属性的过程。
2.1. 基于理想模型的交通工程因素分解
交通工程因素包括:车辆类型、车速、车辆位置、车间距、交通信号、道路状况、防护措施等。这些因素经分解可以转化为以下基本元素:路块长宽、路块位置、路权、道路被占据的状态、道路的通行方向,参与者类型、参与者在整个空间内所处的位置、参与者的瞬时速度,交通控制者类型、交通信号组合、交通指令等。
理想模型包括道路元胞Agent、参与者Agent以及交通控制Agent的Agent,上文提到的基本元素将分别被赋予以上各类Agent,成为它们的属性,以下具体介绍:
2.1.1. 道路元胞Agent属性
道路元胞空间分布如图1所示,定义每个元胞个体对应现实交通中长度为8 m,宽度为4 m的路块。
除了路块长宽外,路块位置、路权、道路被占据的状态以及道路的通行方向转化为以下道路元胞Agent属性:
cell.location(x,y),表示道路元胞Agent在整个元胞空间内所处的位置,(x,y)是道路元胞Agent的坐标序号。
cell.ownership,表示道路元胞Agent的路权归属,0表示路权归行人所有,1归机动车所有。
cell.occupy.state,表示道路元胞Agent被占据的状态,0表示未被占据,1表示被正常占据,2表示冲突下的占据(如某一路块发生车辆追尾事故追尾或者车辆、行人相撞事故等)。

Figure 1. Cellular space of intersection
图1. 交叉口元胞空间
cell.direction,表示道路元胞Agent上的通行方向。0表示禁行,1表示直行,2表示左转向,3表示右转向。该属性允许存在不同数值组合。例如,cell.direction = 1,2表示此区域的车辆既可以直行又可以左转向。
2.1.2. 参与者Agent属性
参与者类型、参与者在整个空间内所处的位置、参与者的瞬时速度转化为以下参与者Agent属性:
participant.type,表示参与者类型,0表示参与者是行人,1表示参与者是机动车。
participant.location(x,y),表示参与者Agent在整个元胞空间内所处的位置,(x,y)是道路元胞Agent的坐标序号。
participant.speed,表示参与者Agent的瞬时速度。
2.1.3. 交通控制Agent属性
交通控制者类型、交通信号组合、交通指令转化为以下交通控制Agent属性:
control.type,表示交通控制者类型,0表示交通控制者是信号灯,1表示交通控制者是交警。
control.signal,表示信号灯给出的交通信号组合。
control.order,表示交警发出的交通指令。
2.2. 基于参与者特征模型的社会心理因素分解
对于特定的交通参与者,影响其随机慢化行为的交通工程因素主要通过感知周边环境而获得,而社会心理因素,如驾驶员性格、情绪、受教育程度,交通法律法规(可以认为是交通参与者自身拥有的一类知识)等,则存在于参与者自身。
参与者特征模型中,通过引入知识库系统对理想模型中的参与者Agent进行拓展,从而体现交通参与者复杂的社会心理特征。社会心理因素可以转化为以下基本元素:性别、年龄、职业、文化程度、驾龄、对法规条文的认知程度等,以上基本元素将被归入知识库系统,作为参与者Agent属性。
如图2所示,计划行为理论[12] 指出,交通参与者对于周边环境的外在感知(包括感知对象、感知范围等)以及主观规范是由其所受教育决定的;而交通参与者对于交通情景的态度以及对认知行为的控制则是由其心理决定的。本文中,外在已确定为对于交通工程因素组成要素的感知,因此,“文化程度”决定了交通参与者的主观规范;性别、年龄、职业、驾龄、对法规条文的认知程度同属于心理影响因素,其中,性别、年龄、职业、驾龄构成交通参与者对于特定交通情景的态度,而对法规条文的认知程度则作为交通参与者的认知行为控制。
如图3所示,Agent知识库系统主要由规划器和决策器组成。外在感知引入周边环境信息;主观规范和态度共同构成了Agent知识库系统的规划器,二者依据参与者对外部交通环境的感知,形成一种或多种的随机慢化行动计划;而认知行为控制则发挥决策器的作用,决定了参与者对于规划器形成的多种行动计划的最终选择。
3. 基于多Agent协同模型的随机慢化影响因素集成
3.1. 多Agent协同模型中的主体参与者Agent
个性化随机慢化机制的形成依靠多Agent协同完成,该协同过程是以每一个参与者Agent为主体进行的,这里定义生成个性化随机慢化机制的参与者Agent为主体参与者Agent。如图4所示,主体参与者Agent可通过获取其他Agent特征(包括感知道路以及与其他参与者之间的交互),并结合自身知识库,形成个性化的随机慢化机制,最终采取随机慢化行为,更新其在元胞空间内的位置。
3.2. 随机慢化行为影响因素集成过程
在多Agent协同模型中,通过多Agent协同设计实现交叉口系统运行过程中不同交通要素之间的交互驱动。基于多Agent协同的个性化随机慢化机制由主体参与者Agent与其他Agent协同完成,主要包括以下三个步骤:
1) 获取其他Agent特征
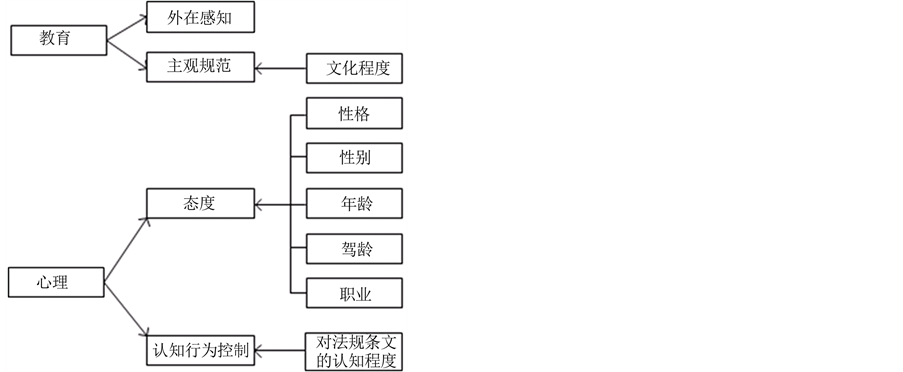
Figure 2.Theory of planned behavior
图2. 计划行为理论

Figure 3. The knowledge base system of traffic participant
图3. 参与者Agent知识库系统

Figure 4. The structure of main traffic participant
图4. 主体参与者Agent结构
获取其他Agent特征是参与者Agent感知外部环境的过程:主体参与者Agent通过感知其他参与者Agent、交通管理Agent以及道路元胞Agent,可以获取基本路况信息。
2) 因素处理
因素处理是基本Agent属性形成影响随机慢化因素的过程:步骤(1)中主体参与者Agent感知其他参与者Agent以及道路元胞Agent,获得的基本路况信息仅是简单的Agent属性,需要通过知识库系统的处理,形成影响随机慢化的因素。例如,某一机动车Agent在获取了前车Agent所在道路元胞坐标以及自身所在道路元胞坐标后,知识库系统就能根据以上数据计算得出该车与前车的车间距。
3) 结合自身特征形成个性化随机慢化机制
步骤(1)、(2)得到的结果是随进慢化行为的外部影响因素。多数情况下,随机慢化行为的影响因素还包括主体参与者Agent自身的性格、心理等,此时,需要知识库系统将内外部因素综合,形成最终的随机慢化机制。
4. 引入个性化随机慢化机制的黄灯困境模拟
4.1. 黄灯困境简述
“黄灯困境”是指黄灯闪烁时,司机在刹车决策上遇到的两难境地。在“通过决策区域”内,司机将会直接通过交叉口;在“制动决策区域”内,司机将会采取刹车制动;在“困境区域内”,司机将会面临两难选择——如果不采取刹车减速,则有可能因为“闯黄灯”而受罚;如果采取刹车减速,则有可能造成追尾事故,这种窘境使得驾驶员不知道何时使用何种决策才能保证不违法又能保证安全通行。
在面临黄灯困境时,驾驶员最终采取的行车决策受到交通管理政策、社会文化环境、自身受教育水平等诸多因素影响,黄灯困境是体现司机随机慢化行为一个典型情景。
4.2. 随机慢化行为影响因素分解
黄灯困境下,影响驾驶员随机慢化行为的交通工程因素为黄灯亮起的时刻“机动车距离交叉口停车线的距离”,该因素可以被分解为以下要素:路块位置坐标、路块长宽,参与者位置坐标,分解的到的要素成为以下Agent属性:cell.location(x,y),participant.location(x,y),路块长宽,以上Agent属性定义见上文。
影响驾驶员随机慢化行为的社会心理因素上文已经做出介绍,经过大量文献调查分析总结,综合考虑驾驶员的各种社会心理因素,可将驾驶员类型分为保守型、冒险型和正常型三类。其中女性中保守型的比例最高,而文化程度为大专以上的冒险型的比率最低。当车辆处于困境区域时,保守型驾驶员选择制动策略的概率最高,而冒险型驾驶员选择通过的概率最高。当考虑驾龄因素时,驾龄越高的驾驶员趋于正常类型的比率最高
4.3. 随机慢化行为影响因素集成
黄灯困境下,以机动车Agent(司机)为主体参与者Agent的随机慢化行为影响因素集成过程如下:
1) 机动车Agent(司机)感知自身所在道路元胞以及停车线所在道路元胞,分别获取二者位置坐标participant.location(x,y),cell.location(x,y)。
2) 知识库系统根据(1)中所得坐标结合路块长宽换算得到机动车Agent当前位置与停车线之间的距离。
3) 知识库系统结合机动车距离停车线的距离、驾驶员类型(社会心理因素的集合),形成最终的个性化随机慢化机制。
4.4. 模拟结果
基于个性化随机慢化机制,本文运用java平台开发了交叉口黄灯困境问题的仿真平台。如图5所示,系统运行36 s后,东西方向(黄灯控制)车道的车流量较好地展现了黄灯困境的交通情景特征,从而验证了本文所建立的个性化随机慢化机制是有效的。
5. 结论
本文基于多Agent协同理论,提出通过多层次Agent模型将共性化的随机慢化概率转化为个性化的随机慢化处理机制的方法:在理想模型和参与者特征模型中,各种影响随机慢化行为的因素被分解归为不同类型Agent的属性;在多Agent协同模型中,参与者Agent通过感知其他Agent,获取影响随机慢化行为的因素,进而结合自身属性,生成个性化的随机慢化机制。本文通过对黄灯困境进行情景模拟,得到与现实交通情景拟合程度较高的模拟结果,个性化随机慢化机制的有效性得以验证。个性化随机慢化机制丰富了交通系统对于随机慢化行为影响因素描述的完整性,增强了随机慢化行为影响因素的可拓展性,降低了随机慢化模型的建模难度,为随机慢化行为的处理提供了新思路。

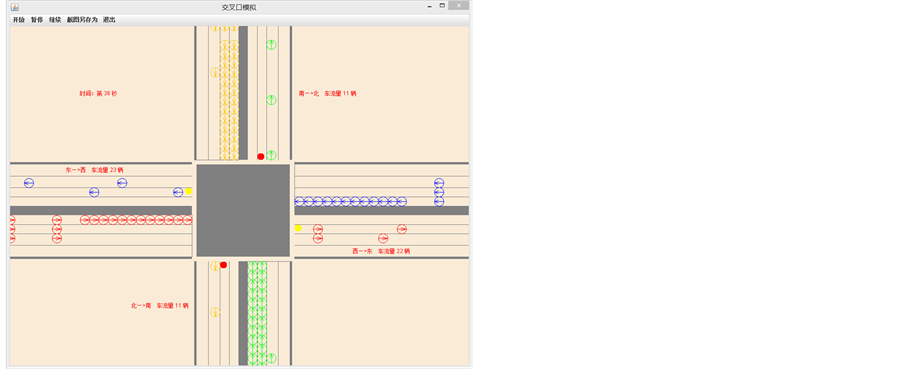
Figure 5. The result of system operation
图5. 系统运行结果
未来研究应丰富知识库系统中由Agent属性形成随机慢化行为影响因素的方法以及综合多种因素形成随机慢化机制的方法,以期进一步完善个性化随机慢化机制。
致 谢
本文为国家自然科学基金项目(NSFC:51278030)。
参考文献 (References)
- [1] Barlovic, R., Santen, L. and Schadschneider, A. (1998) Metastable states in cellular automata for traffic flow. European Physical Journal B, 5,793-800.
- [2] Li, X.B., Wu, Q.S. and Jiang, R. (2001) Cellular automaton model considering the velocity effect of Acar on the successive car. Physical Review E, 64, 066128.
- [3] Jiang, R. and Wu, Q.S. (2006) A stopped time dependent randomization cellular automata Model for traffic flow controlled by traffic light. Physica A, 364, 493-496.
- [4] Li, Q.L., Wang, B.H. and Liu, M.R. (2011) An improved cellular automaton traffic model considering gap-dependent delay probability. Physica A, 390, 1356-1362.
- [5] Mou, Y.B. and Zhong, C.W. (2005) Cellular automaton model of traffic flow based on safety driving. Acta Physica Sinica, 54, 5597-5601. (in Chinese)
- [6] Kuang, H., Kong, L.J. and Liu, M.R. (2004) The study of a cellular automaton traffic flow model with mixed different-maximum-speed vehicles on single lane. Acta Physica Sinica, 53, 2894-2898. (in Chinese)
- [7] Lei, L., Xue, Y. and Dai, S.Q. (2003) One-dimensional sensitive driving cellular automaton model for traffic flow. Acta Physica Sinica, 52, 2121-2126. (in Chinese)
- [8] Bai, K.Z., Tan, H.L., Liu, M.R. and Kong, L.J. (2003) A study on an improved Nagel-Schreckenberg traffic flow model with open boundary conditions. Acta Physica Sinica, 52, 2421-2426. (in Chinese)
- [9] Chen, S.D., Zhu, L.H., Kong, L.J. and Liu, M.R. (2007) The effect of noise-first and anticipation headway on traffic flow. Acta Physica Sinica, 56, 2517-2522. (in Chinese)
- [10] Huang, H.J., Ding, J.X. and Tang, T.Q. (2009) A cellular automaton model of traffic considering the dynamic evolution of velocity randomization probability. Acta Physica Sinica, 58, 7591-7595. (in Chinese)
- [11] 花伟, 许良 (2007)考虑驾驶水平的元胞自动机交通流模型. 交通运输系统工程与信息, 4, 111-114.
- [12] Gou, J.Q. and Guo, S.Y. (2013) Simulation of humanism design of road intersections based on behavior-intensive ca model. Advances in Information Sciences and Service Sciences, 5, 520-528.