Dynamical Systems and Control
Vol.07 No.02(2018), Article ID:24724,8
pages
10.12677/DSC.2018.72013
Synchronization of Fractional-Order Time-Delay Chaotic Systems and Its Application in Secure Communication
Ruoxun Zhang, Yongli Liu, Jingbo Gong
Xingtai University, Xingtai Hebei
Received: Mar. 29th, 2018; accepted: Apr. 23rd, 2018; published: Apr. 30th, 2018

ABSTRACT
This paper studies the synchronization of fractional-order delay chaotic systems. By the stability theorem of fractional-order linear delay systems, a sufficient condition for the global asymptotic stability of fractional time-delay systems is proposed. Combined with the new theory and the characteristics of the chaotic system, a linear controller is designed. Only one state variable needs to be transmitted to achieve the synchronization of the fractional-delay Chen chaotic system, and a secure communication is designed.
Keywords:Fractional-Order Time-Delay Chaotic System, Single-Drive Variable, Secure Communication
分数阶时滞混沌系统的同步和在 保密通信中的应用
张若洵,刘永利,巩敬波
邢台学院,河北 邢台
收稿日期:2018年3月29日;录用日期:2018年4月23日;发布日期:2018年4月30日

摘 要
本文研究了分数阶时滞混沌系统的同步。通过分数阶线性延迟系统的稳定性定理,提出了分数阶时滞系统全局渐近稳定的充分条件。结合新理论和混沌系统的特征,设计了一种线性控制器,只需要传递一个状态量来实现分数阶时滞Chen混沌系统的同步,并设计了一种安全性更好的分数阶混沌保密通信方案。
关键词 :分数阶时滞混沌系统,单驱动变量,保密通信

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
分数阶微积分被认为是传统的整数阶微积分的推广。近年来,它成为一种非常有用的工具来描述各种系统的演变。在许多情况下,用分数阶描述系统比采用整数阶描述更加充分、精确。目前,分数阶微积分被广泛应用于物理,控制工程和信号处理等各个领域 [1] - [6] 。许多研究人员广泛研究了分数阶动力系统的问题,并提出了一些重要的结果 [7] - [13] 。近来,研究分数阶混沌系统已成为一个积极的研究领域。许多研究人员研究了分数阶混沌系统的控制和同步。已经提出了一些实现混沌稳定性或同步性的方法,如PC方法,耦合方法 [14] [15] ,非线性状态观测器方法 [16] [17] ,自适应控制 [18] [19] [20] ,主动控制方法 [21] ,滑模控制 [22] [23] 和投影同步 [24] 。值得指出的是,这些关于分数阶混沌系统的同步的论文主要是无时滞的,或者这些论文中提出的控制器是非线性反馈。在实际工程过程中,许多系统经常遇到时间延迟。对于动态系统,时滞通常会导致系统不稳定并降低系统性能。混沌系统的稳定性通常是某些应用的先决条件。因此,在混沌系统的实际应用中,时滞模型更为普遍。同时,线性反馈控制特别有吸引力,由于其简单的配置和实现,已经被普遍应用于实际之中。在本文中,通过比较定理和一类分数阶线性延迟系统的稳定性定理,得到了分数阶时滞混沌系统的全局渐近稳定的充分条件。基于该理论和混沌系统的特点,设计了一种线性反馈控制器,实现了分数阶时滞混沌系统的同步,并设计了一种安全性更好的分数阶混沌保密通信方案。
2. 预备知识
定义2.1. 阶次为α的函数x(t)的Caputo微分定义为
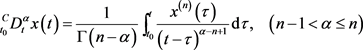 (1)
(1)
引理2.1. ( [25] )设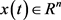 为可微向量函数。则对于
为可微向量函数。则对于 和
和 有
有
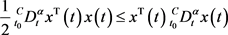 (2)
(2)
引理2.2. [26] 设连续可微函数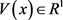 为
为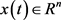 的Lyapunov函数,并且满足
的Lyapunov函数,并且满足
 (3)
(3)
其中 ,
,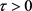 为时滞时间h(t)在时间区间
为时滞时间h(t)在时间区间 连续。如果
连续。如果 ,那么
,那么 。
。
Theorem 2.1. 考虑如下分数阶时滞系统:
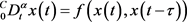 (4)
(4)
其中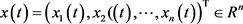 和
和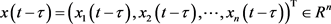 分别是状态向量和时滞状态向量,
分别是状态向量和时滞状态向量,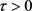 是时滞;
是时滞;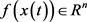 是非线性向量,
是非线性向量,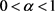 。如果存在两个常数
。如果存在两个常数 和
和 且
且
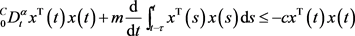 (5)
(5)
那么分数阶时滞系统(4)渐进稳定,即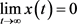 .
.
证明:因为
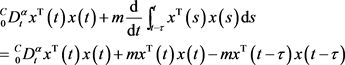
所以由(5)得
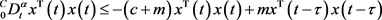 (6)
(6)
设 ,则式(6)变为
,则式(6)变为
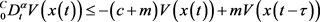
常数 和
和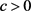 ,有
,有 ,根据引理2.2,
,根据引理2.2, ,即
,即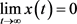 。
。
3. 分数阶时滞混沌系统的线性同步
考虑分数阶Chen时滞混沌系统
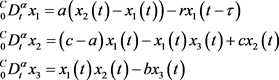 (7)
(7)
当 和
和 ,系统(7)的动力学行为是混沌的。当
,系统(7)的动力学行为是混沌的。当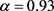 时,最大Lyapunov指数为0.9366,吸引子如图1所示。
时,最大Lyapunov指数为0.9366,吸引子如图1所示。
系统(7)为驱动系统,具有单一状态参量的控制器的响应系统为
 (8)
(8)
定义系统同步误差 ,选取控制器为
,选取控制器为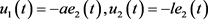 。当选取l > 31.5时,系统(8)与(7)渐进同步。
。当选取l > 31.5时,系统(8)与(7)渐进同步。
证明:由系统(8)和(7)可得误差系统
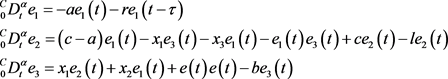 (9)
(9)

Figure 1. Attractors of fractional-order Chen chaotic system with time-delay (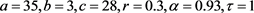 )
)
图1. 分数阶Chen时滞混沌系统的吸引子( )
)
设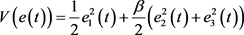 ,(
,( ),则
),则
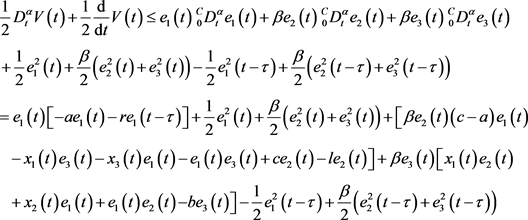
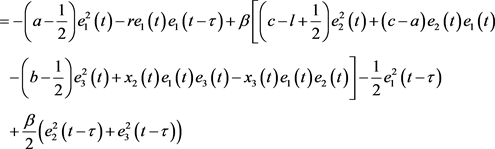
由于混沌的有界性,存在一个正常数M,满足 ,所以
,所以
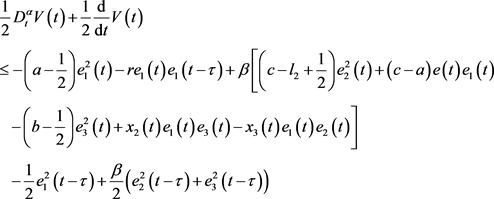
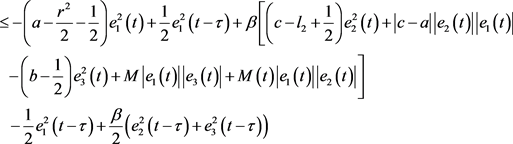
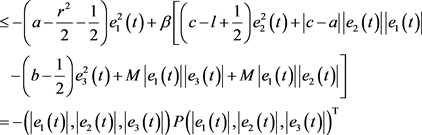
其中

如果下面两个不等式成立,则P是正定的

所以如果 ,其中
,其中 ,P是正定的。从吸引子看
,P是正定的。从吸引子看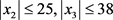 ,取
,取 ,当
,当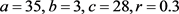 时,
时, ,取
,取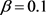 ,当
,当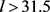 时,P是正定的。这时有
时,P是正定的。这时有
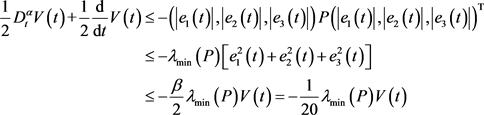
其中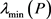 是正定矩阵P的最小特征值.根据Theorem 2.1,系统(8)和(7)同步。图2为l = 32时,系统的同步误差。
是正定矩阵P的最小特征值.根据Theorem 2.1,系统(8)和(7)同步。图2为l = 32时,系统的同步误差。
4. 分数阶时滞混沌系统的线性同步在保密通信中的应用
保密通信数学模型:
发射系统:

Figure 2. Synchronization errors evolution of systems (8) and (7)
图2. 系统(8)和(7)的同步误差演变
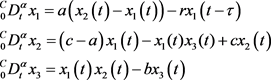 (10)
(10)
发射信号: 和
和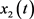
接收系统:
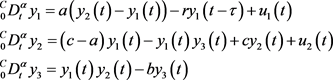 (11)
(11)
控制器为
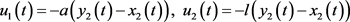
恢复信号为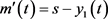 。
。
选择 和
和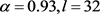 ,信息信号
,信息信号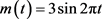 ,对所提出的通信方案进行数值模拟,结果如图3所示;我们搭建电路进行模拟,结果如图4所示。
,对所提出的通信方案进行数值模拟,结果如图3所示;我们搭建电路进行模拟,结果如图4所示。
5. 结论
本文研究了分数阶时滞混沌系统的混沌同步和和在保密通信中的应用问题。基于非线性时滞系统的一个特殊定理,导出了分数阶时滞混沌系统的线性反馈。可以看出,该方法可应用于其他分数阶时滞混沌系统,也可以导出线性控制器。基于比较定理和一类分数阶线性延迟系统的稳定性定理,得到了分数阶时滞混沌系统的全局渐近稳定的充分条件。并用该理论和混沌系统的特点,设计了一种线性反馈控制器,实现了分数阶时滞混沌系统的同步,设计了一种安全性更好的分数阶混沌保密通信方案。
 (a)
(a) 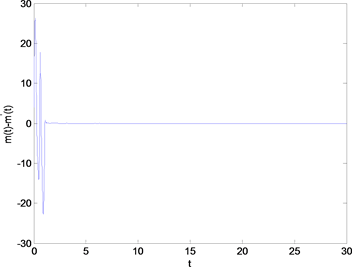 (b)
(b)
Figure 3. Simulation results of the communication scheme. (a) is the recovered signal, and (b) is the error between the original signal and the recovered signal
图3. 通信方案模拟结果(a)为恢复信号,(b)为原信号与恢复信号之间的误差
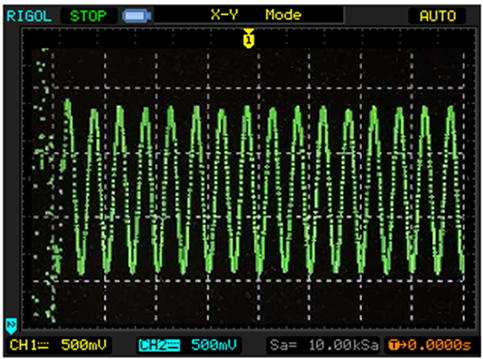
Figure 4. Circuit simulation results-the recovered signal 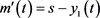
图4. 电路模拟结果-恢复的信号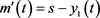
基金项目
邢台市科技支撑计划项目(项目编号:2016ZC191)。
文章引用
张若洵,刘永利,巩敬波. 分数阶时滞混沌系统的同步和在保密通信中的应用
Synchronization of Fractional-Order Time-Delay Chaotic Systems and Its Application in Secure Communication[J]. 动力系统与控制, 2018, 07(02): 116-123. https://doi.org/10.12677/DSC.2018.72013
参考文献
- 1. Heaviside, O. (1971) Electromagnetic Theory. Chelsea, New York. (Reprint of Volumes 1 (1893), 2 (1899) and 3 (1912)).
- 2. Hilfer, R. (2000) Applications of Fractional Calculus in Physics. World Scientific Singapore, Singapore.
https://doi.org/10.1142/3779 - 3. Kilbas, A. and Srivastava, H. and Trujillo, J. (2006) Theory and Applications of Fractional Differential Equations. Elsevier, Boston.
- 4. Koeller, R.C. (1984) Application of Fractional Calculus to the Theory of Viscoelasticity. Journal of Applied Mechanics, 51, 299-307.
https://doi.org/10.1115/1.3167616 - 5. Magin, R.L. (2010) Fractional Calculus Models of Complex Dynamics in Biological Tissues. Computers & Mathematics with Applications, 59, 1586-1593.
https://doi.org/10.1016/j.camwa.2009.08.039 - 6. Podlubny, I. (1999) Fractional Differential Equations. Academic Press. San Diego.
- 7. Deng, W.H., Li, C.P. and Lu, J.H. (2007) Stability Analysis of Linear Fractional Differential System with Multiple Time Delays. Nonlinear Dynamics, 48, 409-416.
https://doi.org/10.1007/s11071-006-9094-0 - 8. Hadi, D., Dumitru, B. and Jalil, S. (2012) Stability Analysis of Caputo Fractional-Order Nonlinear Systems Revisited. Nonlinear Dynamics, 67, 2433-2439.
https://doi.org/10.1007/s11071-011-0157-5 - 9. Lazarevic, M. (2011) Stability and Stabilization of Fractional Order Time Delay Systems. Scientific Technical Review, 61, 123-137.
- 10. Li, Y., Chen, Y.Q. and Podlubny, I. (2009) Mittag-Leffer Stability of Fractional Order Nonlinear Dynamic Systems. Automatica, 45, 1965-1969.
https://doi.org/10.1016/j.automatica.2009.04.003 - 11. Lu, J.G. and Chen, Y. (2013) Stability and Stabilization of Fractional-Order Linear Systems with Convex Polytopic Uncertainties. Fractional Calculus and Applied Analysis, 16, 142-157.
https://doi.org/10.2478/s13540-013-0010-2 - 12. Sabatier, J., Moze, M. and Farges, C. (2010) LMI Sta-bility Conditions for Fractional Order Systems. Computers & Mathematics with Applications, 59, 1594-1609.
https://doi.org/10.1016/j.camwa.2009.08.003 - 13. Stamova, I. and Stamov, G. (2014) Stability Analysis of Im-pulsive Functional Systems of Fractional Order. Communications in Nonlinear Science and Numerical Simulation, 19, 702-709.
https://doi.org/10.1016/j.cnsns.2013.07.005 - 14. Zhu, H., Zhou, S.B. and He, Z. (2009) Chaos Syn-chronization of the Fractional-Order Chen’s System. Chaos, Solitons and Fractals, 41, 2733-2740.
https://doi.org/10.1016/j.chaos.2008.10.005 - 15. Li, C.P. and Deng, W.H. (2006) Chaos Synchronization of Fractional-Order Differential Systems. International Journal of Modern Physics B, 20, 791-803.
https://doi.org/10.1142/S0217979206033620 - 16. Lu, J.G. (2006) Nonlinear Observer Design to Synchronize Fractional-Order Chaotic System via a Scaler Transmitted Signal. Physica A, 359, 107-118.
https://doi.org/10.1016/j.physa.2005.04.040 - 17. Wu, X.J., Lu, H.T. and Shen, S.L. (2009) Synchronization of a New Fractional-Order Hyperchaotic System. Physics Papers A, 373, 2329-2337.
https://doi.org/10.1016/j.physleta.2009.04.063 - 18. Zhang, R.X. and Yang, S.P. (2010) Adaptive Synchronization of Fractional-Order Chaotic Systems. Chinese Physics B, 19, Article ID: 020510.
https://doi.org/10.1088/1674-1056/19/2/020510 - 19. Zaid, M. (2010) Odibat, Adaptive Feedback Control and Synchronization of Non-Identical Chaotic Fractional Order Systems. Nonlinear Dynamics, 60, 479-487.
https://doi.org/10.1007/s11071-009-9609-6 - 20. Zhang, R.X. and Yang, S.P. (2011) Adaptive Synchronization of Fractional-Order Chaotic Systems via a Single Driving Variable. Nonlinear Dynamics, 66, 831-837.
https://doi.org/10.1007/s11071-011-9944-2 - 21. Srivastava, M., Ansari, S.P., Agrawal, S.K., Das, S. and Leung, A.Y.T. (2014) Anti-Synchronization between Identical and Non-Identical Fractional-Order Chaotic Systems using Active Control Method. Nonlinear Dynamics, 76, 905-914.
https://doi.org/10.1007/s11071-013-1177-0 - 22. Zhang, R.X. and Yang, S.P. (2012) Robust Chaos Synchroniza-tion of Fractional-Order Chaotic Systems with Unknown Parameters and Uncertain Perturbations. Nonlinear Dynamics, 69, 983-992.
https://doi.org/10.1007/s11071-011-0320-z - 23. Zhang, R.X. and Yang, S.P. (2013) Robust Synchronization of Two Different Fractional-Order Chaotic Systems with Unknown Parameters using Adaptive Sliding Mode Approach. Nonlinear Dynamics, 71, 269-278.
https://doi.org/10.1007/s11071-012-0659-9 - 24. Zhang, L.G. and Yan, Y. (2014) Robust Synchronization of Two Different Uncertain Fractional-Order Chaotic Systems via Adaptive Sliding Mode Control. Nonlinear Dynamics, 76, 1761-1767.
https://doi.org/10.1007/s11071-014-1244-1 - 25. Aguila-Camacho, N., Duarte-Mermoud, M.A. and Gallegos, J.A. (2014) Lyapunov Functions for Fractional Order Systems. Communications in Nonlinear Science and Numerical Sim-ulation, 19, 2951-2957.
https://doi.org/10.1016/j.cnsns.2014.01.022 - 26. Chen, L, Wu, R., Cao, J. and Liu, J.-B. (2015) Stability and Synchronization of Memristor-Based Fractional-Order Delayed Neural Networks. Neural Networks, 71, 37-44.
https://doi.org/10.1016/j.neunet.2015.07.012