Dynamical Systems and Control
Vol.
12
No.
02
(
2023
), Article ID:
64024
,
12
pages
10.12677/DSC.2023.122009
基于自适应控制的船舶轨迹跟踪算法研究
张祎
天津工业大学,计算机科学与技术学院,天津
收稿日期:2023年3月13日;录用日期:2023年4月10日;发布日期:2023年4月17日

摘要
本篇论文针对带有扰动的自主水面船舶系统,提出了基于自适应律的固定时间滑模控制算法。在控制器的设计中,采用双层嵌套自适应方案以减小抖振现象,控制增益的值根据外部扰动动态变化;将固定时间控制理论应用到船舶轨迹跟踪的研究领域中,能使轨迹误差不受初始运动状态的影响,在固定时间内到达滑模面。另外,提出的控制方法能保证船舶运动轨迹的有界性。最后,设计了一个仿真实验,证明所提方法的有效性及可行性。
关键词
滑模控制,自适应律,固定时间稳定,船舶系统

Research on Ships Trajectory Tracking Algorithm Based on Adaptive Control
Yi Zhang
School of Computer Science and Technology, Tiangong University, Tianjin
Received: Mar. 13th, 2023; accepted: Apr. 10th, 2023; published: Apr. 17th, 2023

ABSTRACT
This paper presents a fixed-time sliding mode control algorithm based on adaptive law for ships with disturbance. In the design of the controller, a dual layer nested adaptive scheme is used to reduce the chattering phenomenon, and the value of the control gain changes dynamically according to the external disturbance. Applying the fixed-time control theory to the research field of ships trajectory tracking can make the trajectory error independent of the initial state and reach the sliding surface in fixed time. In addition, the proposed control method can ensure the boundedness of the system trajectory. Finally, a simulation experiment is designed to verify the effectiveness and availability of the proposed method.
Keywords:Sliding Mode Control, Adaptive Law, Fixed-Time Stability, Ships

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近十几年来,多个国家在智能船舶领域取得较大进展,即利用自动控制技术等手段,在船舶航行和货物运输方面实现自主决策和自动安全航行 [1] [2] 。在相关研究领域中,轨迹跟踪是指使船舶按预先设定的轨迹精确移动 [3] ,为了避免实际环境中存在的不确定扰动对系统性能产生消极影响,可以采用滑模控制方法提高系统的鲁棒性 [4] [5] 。滑模控制是一种简单的控制方法,其中滑动模态可以进行设计,从而获得优越的控制效果,其优势体现在两方面,首先,调节的参数少,响应速度快;其次,对参数变化和扰动有很强的抑制能力,这对于在复杂环境下工作的机器来说非常有利,使得系统受到外部干扰时具有较强的稳定性,这两个特性使得滑模控制方法受到广泛关注 [6] [7] 。例如,文献 [8] [9] [10] [11] 分别研究了水下航行器、直升机系统、飞行器系统和机器人系统的滑模控制方案。
然而,当系统状态到达滑模面之后,难以严格地沿着滑模面向平衡点滑动,而是在滑模面两侧来回运动,从而产生抖振效应。这种抖振容易激发系统的未建模特性,给滑模控制在实际系统中的应用带来困难。为了解决这个问题,文献 [12] 引入边界层和饱和函数的概念,但边界层的厚度需要自适应调整,导致要提前知道扰动值,使系统的鲁棒性降低;文献 [13] 研究了高阶滑模控制方法,具有较高的控制精度,但其实现复杂。文献 [14] 将控制增益设计为时变函数,有效降低了抖振。
从系统稳定的角度来看,确保船舶的轨迹在一个可以提前预算出的时间段内跟踪到期望轨迹,也是船舶的轨迹跟踪控制中必须研究的问题。固定时间稳定是有限时间稳定的一个拓展,能为船舶的实际工作节省成本,带来更多便利。文献 [15] 设计了固定时间扩展状态观测器,能提供快速准确的响应和良好的抖振抑制;文献 [16] 研究了耦合不连续神经网络的固定时间同步问题,该控制律下计算出的稳定时间估计值的上界更加准确。文献 [17] 设计了一个反馈控制器,能够为神经网络固定时间同步提供充分条件。文献 [18] 设计了一种基于固定时间扰动观测器的反步控制方案,利用观测器来估计和补偿跟踪误差的不确定性和柔性效应,使用的滤波器能够避免复杂度过高的问题,从而保证稳定性。
根据以上分析,如何在保证船舶运动固定时间稳定的同时,用一种相对简单且易于实现的控制方法减小控制器的抖振幅度和频率,是一个有待研究和解决的问题。因此,本篇论文研究了一种基于自适应控制的船舶轨迹跟踪固定时间滑模控制算法,使时变的控制增益按照期望趋势变化,在到达滑模面之前尽可能大,在到达之后尽可能小。在这种方案下,增益由一组双层嵌套自适应律表示,确保了到达滑模面之前的抗扰动性,有效降低控制器的振幅以减小抖振。在另一方面,通过改进简单线性滑模控制器,实现系统的固定时间稳定,在任何初始状态下,都能保证系统在有限时间内跟踪到理想轨迹。本文的第二章给出了船舶系统的动力学模型,在第三章和第四章中,分别从理论和实验方面证明了此种算法的准确与可行。
2. 船舶系统模型
2.1. 动力学模型
船舶系统的模型描述如下:
(1)
其中 代表位置向量, 代表速度向量, 表示控制输入, 表示外部环境中的扰动。矩阵 、M、 ,和 分别表示如下:
其中 , , , ,
, , , ,m表示船舶的质量, 表示船舶的重心到坐标系原点的距离。旋转矩阵 满足 , 以及 ,其中矩阵 具有以下形式:
将矩阵 和 拆解为 , 。令 , ,对 求导得:
(2)
其中 , , 。于是得到以下船舶动力学模型:
(3)
2.2. 轨迹误差模型
将船舶的期望位置和速度设置为 , ,期望轨迹的动力学方程如下:
(4)
式中 。将位置误差和速度误差定义为 和 ,可以得到船舶系统的轨迹跟踪误差方程为:
(5)
式中 , 。
3. 基于自适应的固定时间滑模控制算法
采用以下滑模变量和控制器:
(6)
式中的常数满足 , , , , , , 。假设扰动的上界值为 ,扰动导数的上界值为 。
定理1. 在滑模面和控制器(6)的控制下,船舶系统会在固定时间
(7)
内到达滑模面,并且实现全局渐近稳定。
证明:对滑模变量s求导可得:
(8)
当轨迹误差处于到达阶段时,构建李雅普诺夫函数 ,并进行求导,则有:
(9)
由于 ,于是有:
(10)
其中 ,于是船舶系统会在固定时间
(11)
之内收敛到滑模面。到达之后, ,于是有
(12)
上式确保了船舶系统向原点收敛的渐近稳定性。
接下来考虑令控制增益 自适应,随着扰动灵活变化。带有自适应项的控制器设计如下:
(13)
令 ,其中
(14)
考虑 的等效控制 ,需要满足 以消除扰动。利用低通滤波的方法,可以得到等效控制的近似估计值为:
(15)
式中 是一个时间常数,应选取较小值。用不等式 表明估计的精度,选取 和 使不等式成立。给标量 和 选取合适的值,满足以下不等式:
(16)
在自适应项和等效控制的估计值之间建立关系式 。为了使扰动能够被完全抵消,将常数的范围选定为 , 。定义第一个误差变量为:
(17)
如果误差变量大于零,那么控制增益的值就一定大于扰动,从而确保滑动发生。将第一层设计为:
(18)
式中 。在系统到达滑模面之前,误差变量 ,控制增益以时变函数 的速率保持增长,之后再下降,使得 趋于零。定义第二个误差变量为:
(19)
式中h满足 。根据 是否已知,可将自适应律的第二层分两种情况设计。
情况一:当 已知时,将第二层设计为:
(20)
式中 。
定理2. 对于系统(5),采用控制律(13),自适应律(18)、(20),那么误差变量 可以收敛到零,从而系统能够到达滑模面,并且函数 和 是有界的。
证明:构建李雅普诺夫函 ,并求导可得:
(21)
首先对 进行求导:
(22)
接下来 求导:
(23)
应用基本不等式 ,则有:
(24)
根据上式可知,变量 和 会在有限时间内趋向于零。从 的定义来看,自适应增益会一直大于扰动值,并且两者差值保持在一个较小的范围内。可以推知, 是有界的,从而 和 也是有界的。
情况二:当 未知时,将第二层设计为:
(25)
式中 。
定理3. 对于自主水面船舶系统(5),采用控制律(13),自适应律(18)、(25),对于给定的 和 ,存在一个标量 满足
(26)
使得误差变量 能够收敛到 ,并且 和 是有界的。
证明:构建李雅普诺夫函数 ,已知 。
当 时, 。对 进行求导,则有:
(27)
根据先前的推导,可得:
(28)
当 时, 成立,于是有:
(29)
根据自适应律的设计, 恒成立。因此 的值总是随着时间增加,并在t = 0时刻取得最小值,于是 也恒成立。如果 ,可以直接得出结论 ;如果 ,根据函数 的定义, 的边界可以表示如下:
(30)
由上式可以看出, 的关系式恰好满足椭圆方程,其中 和 分别对应坐标系中的横轴和纵轴,目的是为 选取一个合适的值确保不等式(26)成立。当函数 在集合 之外时,就会有 驱使函数进入集合 ,并且 是一个不变集。如果 进入了集合 ,那么就会有 成立。当 没有进入集合时, ,对不等式两边进行积分可得:
(31)
式中 。由此,函数 是有界的,从而 , 和 都是有界的。当时间趋于无穷时, 将会趋于零,那么其范围就一定会满足条件 。
接下来讨论 和 的有界性,根据 的定义可得:
(32)
上式表明 是有界的,从而有:
(33)
上式是确保系统发生滑动的充分条件,根据 的定义可得:
(34)
由于 是有界的,且 ,因此:
(35)
上式证明了 的有界性,从而 也是有界的。
情况二的优势在于,扰动导数的上界不需要是已知的,通过给定 ,h和 的值,存在一个足够大的 ,确保有常数 ,使得定理2中的不等式成立。
综合讨论系统的整个运动过程,结合定理1和定理2, 已知时,整个过程是渐近稳定的。在扰动导数的上界未知时,结合定理1和定理3,系统的运动过程也依然是全局渐近稳定的。因此,无论匹配扰动导数的上界是否已知,系统的轨迹误差都会实现全局渐近稳定性。
由以上理论推导可以看出,在外部扰动及其导数值未知的情况下,控制增益能够灵活变化,在很大程度上减弱了扰动对动力学系统的消极影响;同时,在固定时间控制器的作用下,无论初始位置如何变化,到达阶段所用的时间都大致相同。因此,从这两个角度来看,自适应固定时间稳定滑模控制算法的优势在于,消除了一些不确定因素的负面作用,从而提高系统的鲁棒性和稳定性。
4. 数值仿真
将船舶系统的有关参数设置为 , , , , , , , , , , , , , , , , , , , , , 。
将外部扰动设置为: 。定义期望轨迹为:
将滑模变量的系数设置为
将控制增益的值选择为 ,其他相关参数设置为 , , , , 。采用两个不同的初始状态 和 ,滑模变量以及轨迹误差的实验效果分别如图1和图2。可以看出,系统轨迹到达滑模面和轨迹误差收敛到零的时间范围固定,不受初始状态的影响。
在双层嵌套自适应律中,选取常数 , , , , , , 。实际环境中的扰动都是不可测的,因此只展示在扰动导数上界未知情况下的实验结果。采用自适应增益方案后,控制输入的变化情况如图3,增益和扰动的变化情况如图4。控制输入的抖振幅度明显减小到500以下,并且增益能够实时追随着扰动进行动态变化。
根据图4,假设扰动的上界 ,自适应增益的最大值 ,可以计算出稳定时间 。如图5,滑模变量的收敛时间在第2 s之前,满足稳定时间的范围。如图6和图7,在船舶系统开始运动不到5 s时,其位置轨迹和速度轨迹都可以跟踪上期望轨迹 和 ,轨迹误差也在5 s之前趋向于零,实现了较好的跟踪效果。

Figure 1. Sliding mode variable under different initial states
图1. 不同初始状态下的滑模变量
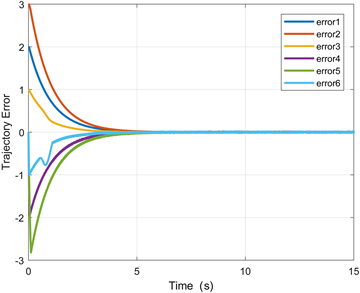
Figure 2. Trajectory error under different initial states
图2. 不同初始状态下的轨迹误差
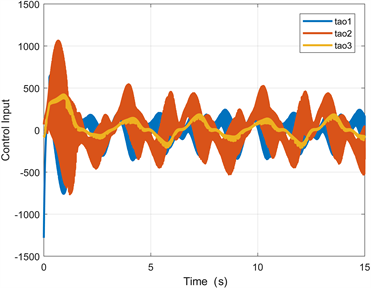
Figure 3. Control input under adaptive gain
图3. 自适应增益下的控制输入
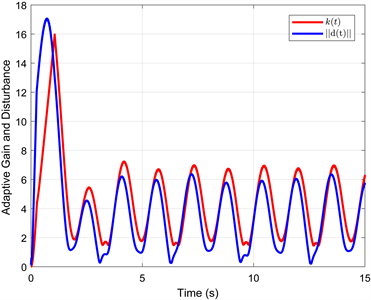
Figure 4. Control gain and norm of disturbance
图4. 控制增益和扰动范数
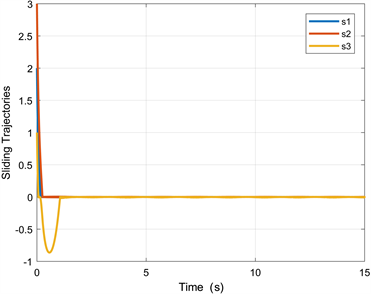
Figure 5. Sliding mode
图5. 滑模变量
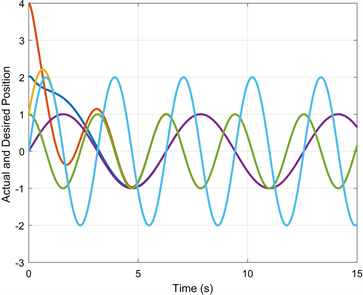
Figure 6. The actual and desired trajectory of autonomous surface vehicle
图6. 船舶系统的真实轨迹与期望轨迹

Figure 7. The trajectory error of autonomous surface vehicle
图7. 船舶系统的轨迹误差
5. 结论
本篇论文针对船舶系统的轨迹跟踪问题,采用了一种固定时间滑模控制器,并且将其中的控制增益设计为自适应的双层嵌套形式,再分别通过理论和实验证明了研究方法的准确性与可行性。一方面,可以实现船舶轨迹误差在到达阶段的固定时间稳定性,即不论初始位置如何变化,总会在固定时间内到达滑模面;另一方面,动态变化的控制增益能灵活地跟随扰动,并且和扰动的误差保持在一个趋于零的小范围内,有效减小了控制器抖振的幅度和频率,节约通信资源。最后通过仿真实例,证明了理论方法的有效性。
文章引用
张 祎. 基于自适应控制的船舶轨迹跟踪算法研究
Research on Ships Trajectory Tracking Algorithm Based on Adaptive Control[J]. 动力系统与控制, 2023, 12(02): 86-97. https://doi.org/10.12677/DSC.2023.122009
参考文献
- 1. 郑华荣, 魏艳, 瞿逢重. 水面无人艇研究现状[J]. 中国造船, 2020, 61(S1): 228-240.
- 2. 李永杰, 张瑞, 魏慕恒, 等. 船舶自主航行关键技术研究现状与展望[J]. 中国舰船研究, 2021, 16(1): 32-44.
- 3. Li, L., Li, J. and Zhang, S. (2021) State-of-the-Art Trajectory Tracking of Autonomous Vehicles. Mechanical Sciences, 12, 419-432.
https://doi.org/10.5194/ms-12-419-2021 - 4. Zhang, J., Zhang, Q. and Wang, Y. (2017) A New Design of Sliding Mode Control for Markovian Jump Systems Based on Stochastic Sliding Surface. Information Sciences, 391-392, 9-27.
https://doi.org/10.1016/j.ins.2017.02.005 - 5. Mishra, R.N. and Mohanty, K.B. (2020) Development and Implementation of Induction Motor Drive Using Sliding-Mode Based Simplified Neuro-Fuzzy Control. Engineering Applications of Artificial Intelligence, 91, Article ID: 103593.
https://doi.org/10.1016/j.engappai.2020.103593 - 6. Zhu, S., Polyakov, A. and Nakonechnyi, O. (2017) Sliding Mode Control Design for Linear Evolution Equations with Uncertain Measurements and Exogenous Perturbations. IFAC-PapersOnLine, 50, 8513-8517.
https://doi.org/10.1016/j.ifacol.2017.08.872 - 7. Feng, J., Gao, S., Zhao, D., et al. (2020) Dynamic Output Feedback Sliding Mode Control for Non-Minimum Phase Systems with Application to an Inverted Pendulum. IFAC-PapersOnLine, 53, 5165-5170.
https://doi.org/10.1016/j.ifacol.2020.12.1182 - 8. Liu, X., Zhang, M., Chen, J., et al. (2020) Trajectory Tracking with Quaternion-Based Attitude Representation for Autonomous Underwater Vehicle Based on Terminal Sliding Mode Control. Applied Ocean Research, 104, Article ID: 102342.
https://doi.org/10.1016/j.apor.2020.102342 - 9. Boukadida, W., Benamor, A., Messaoud, H., et al. (2019) Multi-Objective Design of Optimal Higher Order Sliding Mode Control for Robust Tracking of 2-DoF Helicopter System Based on Metaheuristics. Aerospace Science and Technology, 91, 442-455.
https://doi.org/10.1016/j.ast.2019.05.037 - 10. Zc, A., Tj, B. and Yn, A. (2020) Self-Triggered Sliding Mode Control for Digital Fly-by-Wire Aircraft System. Journal of the Franklin Institute, 357, 10492-10512.
https://doi.org/10.1016/j.jfranklin.2020.08.028 - 11. Qureshi, M.S., Swarnkar, P. and Gupta, S. (2018) A Supervisory On-Line Tuned Fuzzy Logic Based Sliding Mode Control for Robotics: An Application to Surgical Robots. Robotics and Autonomous Systems, 109, 68-85.
https://doi.org/10.1016/j.robot.2018.08.008 - 12. Chen, M., Wu, Q.X. and Cui, R.X. (2013) Terminal Sliding Mode Tracking Control for a Class of SISO Uncertain Nonlinear Systems. ISA Transactions, 52, 198-206.
https://doi.org/10.1016/j.isatra.2012.09.009 - 13. Hao, C.A., St, A., Jh, A., et al. (2021) High-Order Sliding Mode Control of a Doubly Salient Permanent Magnet Machine Driving Marine Current Turbine. Journal of Ocean Engineering and Science, 6, 12-20.
https://doi.org/10.1016/j.joes.2020.04.001 - 14. Hwang, C.-L. (1996) Sliding Mode Control Using Time-Varying Switching Gain and Boundary Layer for Electrohydraulic Position and Differential Pressure Control. Control Theory and Applications, IEE Proceedings, 143, 325-332.
https://doi.org/10.1049/ip-cta:19960377 - 15. Zhang, L., Xia, Y., Shen, G., et al. (2021) Fixed-Time Attitude Tracking Control for Spacecraft Based on a Fixed-Time Extended State Observer. Science China Information Sciences, 64, 1-17.
https://doi.org/10.1007/s11432-019-2823-9 - 16. Hu, C., Yu, J., Chen, Z., et al. (2017) Fixed-Time Stability of Dynamical Systems and Fixed-Time Synchronization of Coupled Discontinuous Neural Networks. Neural Networks, 89, 74-83.
https://doi.org/10.1016/j.neunet.2017.02.001 - 17. Chen, C., Li, L., Peng, H., et al. (2020) A New Fixed-Time Stability Theorem and Its Application to the Fixed-Time Synchronization of Neural Networks. Neural Networks, 123, 412-419.
https://doi.org/10.1016/j.neunet.2019.12.028 - 18. Wang, X., Guo, J., Tang, S., et al. (2019) Fixed-Time Disturbance Observer Based Fixed-Time Back-Stepping Control for an Air-Breathing Hypersonic Vehicle. ISA Transactions, 88, 233-245.
https://doi.org/10.1016/j.isatra.2018.12.013