Advances in Marine Sciences
Vol.
06
No.
02
(
2019
), Article ID:
30628
,
13
pages
10.12677/AMS.2019.62007
Short-Term Prediction of Significant Wave Height Based on EMD Decomposition
Shiyi Kan*, Ting Yu, Li Liu
College of Science, China University of Petroleum (East China), Qingdao Shandong

Received: May 13th, 2019; accepted: May 28th, 2019; published: Jun. 4th, 2019

ABSTRACT
Waves are closely related to human activities at sea, and play an important role in the fields of navigation, marine development, disaster prevention and mitigation. Wave prediction, especially the prediction of significant wave height, has always been the focus of ocean research. Because of the random characteristics and uncertainties of waves, the accuracy of wave prediction is still the key problem to be solved. In this paper, the wave data in Bohai Sea are deeply studied to predict the short-term significant wave height by a hybrid model based on empirical mode decomposition (EMD) and support vector regression (SVR). Empirical mode decomposition (EMD) can adaptively decompose non-stationary time series into a series of intrinsic mode functions (IMFs) and residuals with frequencies from high to low. According to the severity of trend changes of the IMFs, different kernel functions are selected for support vector regression prediction. Then, the weighted combination of each prediction component is used to obtain the accurate prediction value of the original series. The short-term prediction experiment of significant wave height in Bohai Sea in 2012 shows that the hybrid model based on empirical mode decomposition (EMD) and support vector regression model (SVR) is more accurate than the single support vector regression model.
Keywords:Empirical Mode Decomposition, Support Vector Regression, Prediction of Significant Wave Height, Hybrid Model
基于EMD分解的海浪有效波高短期预测研究
阚世宜*,于婷,刘莉
中国石油大学(华东),理学院,山东 青岛

收稿日期:2019年5月13日;录用日期:2019年5月28日;发布日期:2019年6月4日

摘 要
海浪与人类的海上活动密切相关,其在航海运输、海洋开发、防灾减灾等领域中具有重要地位。海浪预报,尤其是海浪有效波高的预报一直是海洋研究的重点。由于海浪具有很多的随机特性和不确定因素,海浪预报的准确度依然是目前要解决的关键问题。本文深入研究了渤海海浪数据,拟采用基于经验模式分解(EMD)和支持向量回归模型(SVR)联合的混合模型进行短期海浪有效波高预测。经验模式分解能够自适应地将非平稳时间序列分解为频率由高到低的一系列本征模函数(Intrinsic Mode Function, IMF)和残差,然后根据本征模函数各自趋势变化的剧烈程度选择不同的核函数进行支持向量回归预测,接着对各预测分量进行加权组合,得到原始序列的准确预测值。渤海2012年的海浪有效波高短期预测实验表明,基于经验模式分解(EMD)和支持向量回归模型(SVR)联合的混合模型预测结果比单一的支持向量回归模型预测结果更准确。
关键词 :经验模式分解,支持向量回归,海浪有效波高预测,混合模型

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
海浪对人类海上作业活动有着巨大的影响,因此进行海浪预报是至关重要的。海浪有效波高短期预测是海洋工程和海岸安全的重要内容。目前有四类方法实现海浪有效波高预测:海浪数值模型,经典的时间序列模型,机器学习模型和混合模型 [1] 。
海浪数值模型要建立在明确的物理过程上,它的预测缺少实时性,所以数值方法的应用还存在一定的局限性。经典的时间序列模型,包括自回归(AR)模型、移动平均(MA)模型、自回归移动平均(ARMA)模型和差分自回归移动平均(ARIMA)模型。但时间序列模型不适用于非线性和非平稳的海浪波高的预测。机器学习方法,能够在不预先了解输入和输出变量之间的关系的情况下进行非线性建模,包括人工神经网络(ANN)模型、遗传算法等。然而,使用一个模型建立非线性和非平稳的时间序列是非常困难的,因为在数据中隐藏了太多可能的模式。因此,研究混合模型提高海浪预报的准确性很有必要。
EMD方法是分析非稳态信号的一种独特分析方法,在理论上可以用于任何类型的信号分解,现主要用于地球物理探测、地震工程、结构损害侦测、潜艇设计、血压变化和心律不整、卫星资料分析等各项研究 [2] 。EMD方法还未普遍应用于海浪有效波高的预测,本文只是一次尝试。应用EMD方法在海浪数据预测海浪有效波高的实验中有很好的效果,但在用风场数据预测海浪有效波高的实验中面临一个问题:风和浪分解后的本征模函数个数不一样,进行SVR预测时找不到有效参数。这是目前待解决的问题。
海浪有效波高为非线性非平稳时间序列,经验模式分解(EMD)方法在分析非线性和非平稳序列方面具有先天的优势。该方法具有自适应、正交性、完备性等特点。Mahjoobi和Mosabbeb (2009)首次将支持向量回归模型应用于海浪有效波高的预测。基于经验模式分解方法的支持向量回归模型克服了支持向量回归模型处理非平稳时间序列能力不强的问题。本文分别采用单一的支持向量回归模型和经验模式分解与支持向量回归模型联合的方法分别对渤海的海浪有效波高建立短期预测模型,对比发现经验模式分解与支持向量回归联合模型取得了更准确的预测效果,弥补了单一的支持向量回归模型预测的滞后性。
2. 研究范围和使用的数据
有效波高是指按一定规则统计的实际波高值。由于海面波浪实际上是各种不同波高、周期、进行方向的多种波的无规则组合,因此一个波浪的波高值没有代表性。为此,在任一个由n个波浪组成的波群中,将波列中的波高由大到小依次排列,确定前n/3个波为有效波。有效波的波高和周期则等于这n/3个波的平均波高和平均周期。
本文研究区域位于渤海,又称渤海湾和直隶湾(Gulf of Chihli)。渤海是一个近封闭的内海,三面环陆,在辽宁、河北、山东、天津三省一市之间。它的具体位置在北纬37˚07'~41˚0'、东经117˚35'~121˚10'。本文从全国数据浮标中心(National Data Buoy Center)获取了北纬38˚9'31、东经121˚40'48的一个浮标上的海浪有效波高资料。数据收集期为2012年12月15日至2013年2月15日,每隔1小时收集一次。但是,2012年12月28日至2013年1月6日期间缺少数据集。海浪有效波高的情况如图1所示。

Figure 1. Significant wave height
图1. 海浪有效波高
3. 模型的建立
被测海浪时间序列是由不同的振荡尺度组成的复杂非线性和非平稳信号。在实现波浪预测时,利用单一模型进行预测多振荡尺度会产生一定的困难。因此,本文在单一模型的基础上选用联合EMD与SVR的混合模型,利用EMD对被测海浪时间序列进行适当的信号预处理来提高SVR模型的预测性能。
3.1. 经验模式分解
经验模式分解法(Empirical mode decomposition, EMD)在1998年由Huang [3] 提出,理论上可以应用于任何类型的时间序列(信号)的分解。它在处理非平稳非线性数据上,比之前的平稳化方法更具有明显的优势。它作为一种完全的数据驱动方法,一经提出就在不同的工程领域得到了迅速有效的应用,如用在海洋、大气、天体观测资料与地球物理记录分析等方面。时间序列的平稳性,一般指宽平稳,即时间序列的均值和方差为与时间无关的常数,其协方差与时间间隔有关而与时间无关 [4] 。这种方法的本质是通过数据的特征时间尺度来获得本征波动模式,从而分解数据。这种分解过程可以形象地称之为“筛选”过程。
EMD分解方法是基于以下假设条件:
1) 数据至少有两个极值,一个最大值和一个最小值;
2) 数据的局部时域特性是由极值点间的时间尺度唯一确定;
3) 如果数据没有极值点但有拐点,则可以通过对数据微分一次或多次求得极值,然后再通过积分来获得分解结果。
经验模式分解的基本思想:将一个频率不规则的波化为多个单一频率的波+残波的形式,即原波形 = + 余波。它的分解过程 [5] 如下:
· 找出原时间数据序列 所有的极大值点和极小值点并用三次样条插值函数拟合形成原数据的上包络线 和下包络线 ,取上包络线和下包络线的均值记作 ,即 。
· 将原数据序列 减去该平均包络 ,得到一个新的数据序列 ,即 。
· 验证 是否满足IMF的条件,若还存在负的局部极大值和正的局部极小值,则执行步骤1)到步骤2),直到 是本征模函数为止。
· 经过n个转移过程后,将得到第n个IMF组分 和相应的残差,重复整个算法,当残差变为单调函数时,停止迭代。
· 最终得到分解后的时间数据序列方程: 。
3.2. 支持向量回归
3.2.1. 支持向量回归的应用性
支持向量机(Support Vector Machines, SVM) [6] 是20世纪90年代Vapnik提出的一种新的机器学习方法并被广泛应用于解决高度非线性分类和回归问题。支持向量回归机(Support Vector Regression, SVR) [7] 是其重要的应用分支。在结构风险最小化的假设下,SVR能最小化经验性风险和学习机器的置信区间,以达到良好的泛化能力。
3.2.2. 支持向量回归的理论基础
根据给定的波高时间序列 可以得到训练数据集 ,其中输入数据 是一个m维向量,输出数据 是基于m维空间上的线性回归函数。
下面给出SVR模型的估计:
(1)
其中W是m维加权向量, 是m维向量函数,(·)表示内积运算,b是标量,N为训练样本个数。它的基本思想是一个非线性函数通过使用一组基函数 和权重系数W转换为线性形式。支持向量机方法的目的是将经验风险和整体拟合误差降到最小,W和b通过最小化下列泛函进行估计。
(2)
式中 为SVR的实际输出; 为e不敏感损失函数,它能够用稀疏数点表现,其定义如下:
(3)
式(3)表明若SVR的输出 与实际输出 的绝对值小于设定的ε时,损失函数值可忽略不计;否则令损失函数的值大于0,其大小为 超出ε的部分。从而使回归问题等同于下面的优化问题。
(4)
其中C是正则化常数, 是估计误差。为了求解优化问题,引入拉格朗日函数L (Vapnik, 1998)。
(5)
在这里 表示拉格朗日乘子。利用拉格朗日函数,方程(4)中的优化问题得到了(6)所示的Karush-Kuhn-Tucker (KKT)条件。Vapnik (1998)给出了线性方程组(6)的详细推导和数学证明。
(6)
线性方程组(6)可以进一步写成
(7)
其中, ,I是一个单位矩阵, , 是一个核函数。
核函数的选择没有一般的指导原则,不同的核函数适用于不同的问题。广泛使用的内核函数包括:线性函数、σ函数、多项式函数和径向基函数(RBF)。其中径向基函数(RBF)不仅易于实现,而且还具有将训练数据非线性地映射到无限维空间的特点。Mahjoobi和Mosabbeb (2009)也证明,带有RBF核的SVR模型在海浪预报中表现良好。因此,本文采用了RBF核函数 [8] 。
宽度为β的RBF函数表示为
(8)
(9)
其中 为输入向量, 为RBF核函数的参数。通过求解线性方程组(7),可以得到SVR模型中b和a的参数,并将回归函数改写为:
(10)
在SVR模型中,RBF的参数 和SVM模型的惩罚参数C,将对预测结果产生很大的影响 [9] 。
3.3. 联合EMD与SVR的有效波高短期预测模型建立
在海浪有效波高预测的EMD-SVR模型的实现过程中包括三个步骤。首先,海浪有效波高时间序列由EMD进行平稳化处理,得到一系列的不同频率的平稳分量,即本征模函数(IMF)和残差,它们更能准确地反映海浪的特征信息。根据这些分量的变化规律建立不同的SVR预测模型,最后通过对分量的预测结果进行等权叠加组合,得到最终预测结果 [10] 。如下图2所示。

Figure 2. EMD-SVR model building diagram
图2. EMD-SVR模型建立图
SVR回归算法可实现线性或非线性的函数映射,其训练过程实际就是一个优化计算的过程,故可应用SVR实现组合预测。其基本思想是:将各个IMF的SVR同时刻的预测结果作为输入,将同时刻的相应的实际值作为输出。然后对网络进行足够的学习训练,直到找到最优参数为止 [11] 。从而使得各个参加组合预测的分量和实际输出值之间建立一种非线性映射关系。对于训练好的网络,当输入端为各个不同IMF的SVR预测值时,其输出即为组合后的最终预测值。
3.4. 统计参数
为了定量比较模型的性能,观察和预测有效波高的值,我们计算了均方根误差(RMSE)、相关系数(R)和一致性指数(IA)进行统计比较。这些统计指标被定义为
(11)
(12)
(13)
其中, 是观测到的(预测的)参数,n表示目标预测的SWH的总数, 是观测(预测)参数的平均值。
4. 渤海海浪有效波高预测实验
在本实验中,将数据集分为两部分。一部分是810个有效波高组成的训练数据,它被用来建立模型。另一部分是剩下的480个有效波高,它作为测试数据对模型进行验证。
将从浮标收集的渤海海浪有效波高数据进行处理,对于缺失数据,用前一小时的海浪有效波高代替。为了避免经验模式分解之后产生的本征模函数及残差的个数不同,将训练集与测试集作为整体进行分解,分解情况如下图3。
从图中可以看出,分解后的分量表现出更强的规律性,能较好的反映海浪特征。IMF1为海浪剧烈变化的高频分量,数值较小,反映海浪受随机因素的影响;IMF2、IMF3数值小,为高频周期分量;IMF4,IMF5有部分高频与原始负荷变化相似,数值大,有周期性,平缓变化,为基本海浪周期分量;IMF6、IMF7数值小,为低频周期分量;IMF8为趋势项及残差。
根据不同分量的特征,分别选择合适的核函数,采用交叉验证和网格搜索法确定SVR模型中的参数。最终在各个分量的最优核函数参数条件下,对所有组件的预测进行等权叠加汇总,达到最终的预测结果。分别对0,3,6,9,12时后的海浪进行预测,预测结果如下图4,且评价指标在下表1。
从图4中可以看出,EMD-SVR模型对0小时海浪有效波高的预测与实际观测值拟合地非常好,对3小时海浪有效波高的预测除了极个别最高点达不到之外,预测值几乎与实际观测值重合,而6,9,12小时海浪有效波高的预测结果不如0,3小时海浪有效波高的预测结果。
为了对比验证混合模型的有效性和可行性,用单一的SVR模型也对0,3,6,9,12时后的海浪有效波高进行预测,预测结果如下图5,且评价指标在下表2。
从图5中可以看出,SVR模型对0小时海浪有效波高的预测与实际观测值拟合地非常好,对3小时海浪有效波高的预测与实际观测值整体趋势相同,但是存在滞后性,而6,9小时海浪有效波高的预测结果与实际观测值大体上拟合,但滞后性更严重,而12小时海浪有效波高的预测结果与实际观测值拟合效果较差。
通过对比可以发现,单一的SVR模型进行预测时存在明显的滞后性,而EMD-SVR模型很好的改善了这一点,而从评价指标来看,EMD-SVR模型比单一的SVR模型的预测结果均方根误差更小,相关系数更大,一致性指数也大。因为EMD将非平稳的原始海浪有效波高时间序列分解为一系列平稳的具有一定规律的单一分量,跟原始海浪有效波高序列相比,这些分量更易预测;其次,与传统的神经网络方法相比,SVR不是以经验风险最小化为原则,而是建立在结构风险最小化原理基础上,通过调整常数,使误差尽可能小的同时,使回归函数尽可能平滑,故它具有更强的推广能力。
同时,可以发现无论是单一的SVR模型还是EMD-SVR模型,其在0,3,6小时的预测结果明显优于9,12小时后的预测结果。

Figure 3. EMD decomposition graph
图3. EMD分解图
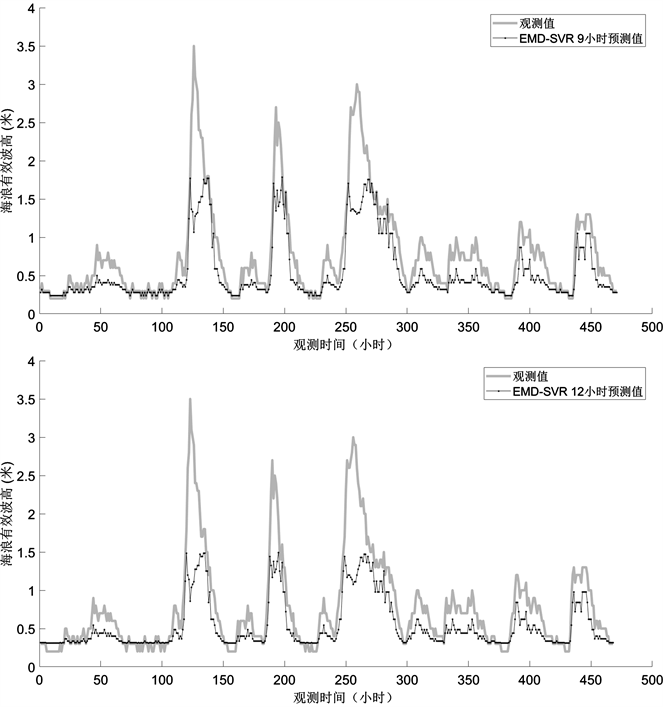
Figure 4. Predicted and observed values of EMD-SVR at different time points
图4. EMD-SVR在各个时间点的预测值与观察值
Table 1. Error index of EMD-SVR prediction at different time points
表1. EMD-SVR预测各个时间点的误差指数
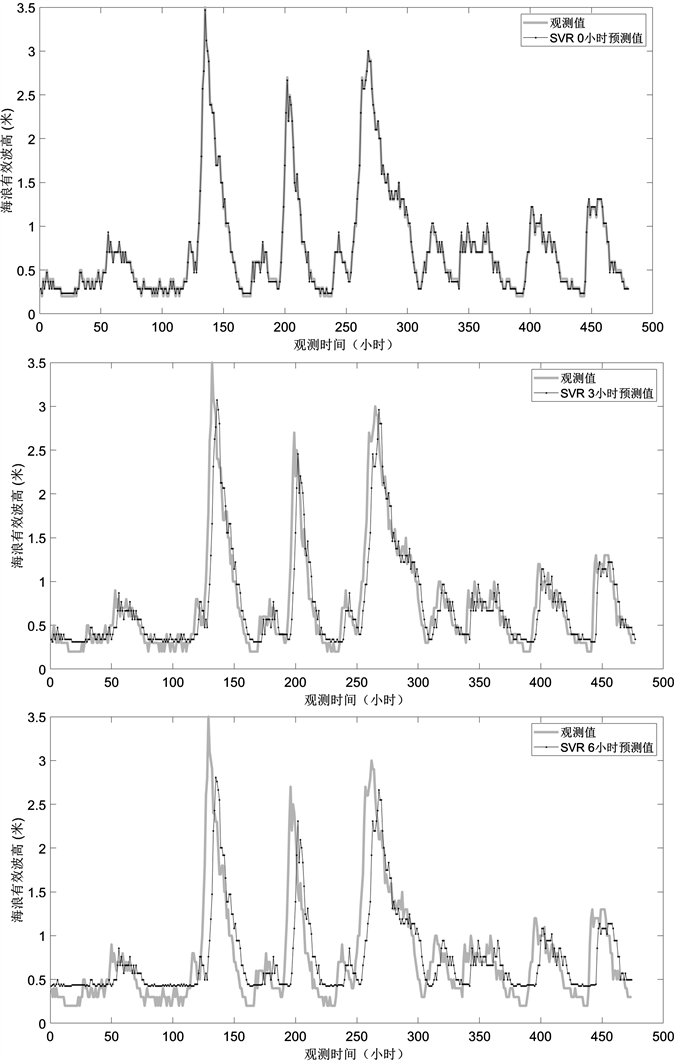

Figure 5. Predicted and observed values of SVR at various time points
图5. SVR在各个时间点的预测值与观察值
Table 2. Error index of SVR prediction at different time points
表2. SVR预测各个时间点的误差指数
5. 结论
将海浪有效波高时间序列用EMD进行平稳化处理,能得到一系列的不同频率的平稳分量,这些分量更能准确地反映原始序列的特征信息。根据这些分量的变化规律建立不同的SVR子模型,最后通过SVR对子模型进行等权叠加得到最终预测结果。试验结果表明,EMD-SVR模型具有良好的预测能力,弥补了单一的SVR模型的滞后性。
基金项目
中国石油大学(华东)大学生创新创业训练项目。
文章引用
阚世宜,于 婷,刘 莉. 基于EMD分解的海浪有效波高短期预测研究
Short-Term Prediction of Significant Wave Height Based on EMD Decomposition[J]. 海洋科学前沿, 2019, 06(02): 51-63. https://doi.org/10.12677/AMS.2019.62007
参考文献
- 1. Duan, W.Y., Han, Y., Huang, L.M., Zhao, B.B. and Wang, M.H. (2016) A Hybrid EMD-SVR Model for the Short-Term Prediction of Significant Wave Height. Ocean Engineering, 124, 54-73. https://doi.org/10.1016/j.oceaneng.2016.05.049
- 2. Huang, W., Shen, Z., Huang, N.E. and Fung, Y.C. (1998) Engineering Analysis of Biologicall Variables: An Example of Blood Pressure over 1 Day. Proceedings of the National Academy of Sciences of the United States of America, 95, 4816-4821. https://doi.org/10.1073/pnas.95.9.4816
- 3. Rilling, G., Flandrin, P. and Goncalves, E. (2003) On Empirical Mode Decomposition and Its Algorithms. Proceeding of IEEE EUSIPCO Work, 2003, 8-11.
- 4. 潘红宇, 编著. 时间序列分析[M]. 北京: 对外经济贸易大学出版社, 2006.
- 5. Balocchi, R., Menicucci, D. and Varanini, M. (2003) Empirical Mode Decomr Position to an Approach the Problem of Detecting Sources from a Reduced Number of Mixtures. Proceeding of the 25th Annual International Conference of the IEEE EM BS, 4, 2443-2446.
- 6. 张春友, 闫伟, 吴晓强, 等. 基于SVR的图书馆数字资源服务绩效评价方法[J]. 现代电子技术, 2018, 41(22): 21-24, 29.
- 7. 李亚巍, 卞双. 支持向量回归机理论及其应用[J]. 中国电力教育, 2005(S2): 183-184.
- 8. 肖建, 于龙, 白裔峰. 支持向量回归中核函数和超参数选择方法综述[J]. 西南交通大学学报, 2008, 43(3): 297-303.
- 9. 杨玫, 刘瑜, 孔波. SVR模型参数选择方法的研究[J]. 计算机时代, 2009(11): 53-55.
- 10. 姚琦, 牛瑞卿, 赵金童, 等. 基于经验模式分解–支持向量机的滑坡位移预测方法研究[J]. 安全与环境工程, 2017, 24(1): 26-32.
- 11. 王巍, 赵宏, 梁朝晖, 等. 基于EMD和SVR的混合智能预测模型及实证研究[J]. 计算机工程与应用, 2012, 48(4): 225-227.
NOTES
*通讯作者。
