Geomatics Science and Technology
Vol.06 No.03(2018), Article ID:25956,8
pages
10.12677/GST.2018.63021
Point Cloud Data Registration Based on Least Squares
Kun Chen, Yuefeng Lu*, Xiaorong Chu, Lijuan Lu
Shandong University of Technology, Zibo Shandong

Received: Jun. 23rd, 2018; accepted: Jul. 11th, 2018; published: Jul. 18th, 2018

ABSTRACT
Based on the principle of least squares, this paper studies the point cloud three-dimensional coordinate transformation model and iterative solution method. It introduces a method that solves the rotation matrix’s elements as an unknown parameter without seeking the rotation angle, and converts the original seven-parameter model into a thirteen-parameter model, and the model and solution to solve the parameters are introduced. It compensates for the shortcomings of the traditional seven-parameter method in the face of large rotation angle. This method can solve the three-dimensional coordinate transformation of arbitrary rotation angle.
Keywords:Point Cloud, Least Squares, Three-Dimensional Coordinate Transformation
基于最小二乘原理的点云数据配准
陈坤,逯跃锋*,楚潇蓉,陆黎娟
山东理工大学,山东 淄博

收稿日期:2018年6月23日;录用日期:2018年7月11日;发布日期:2018年7月18日

摘 要
基于最小二乘原理,本文研究了点云三维坐标转换的模型及其迭代解法,介绍了一种不求旋转角度而将旋转矩阵的元素作为未知参数进行求解的方法,将原本的七参数模型转换成十三参数模型,介绍了求解参数的模型和解法。弥补了传统七参数法在面对大旋转角时的不足,该方法能够解决任意旋转角的三维坐标转换。
关键词 :点云,最小二乘,三维坐标转换

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
三维激光扫描技术是近十几年迅速发展起来的一项三维数据获取的新兴技术。它可以通过对研究对象数字化,得到大量点的三维坐标集合,称为点云数据。
点云配准实质是将扫描采样获得的不同扫描坐标系下的两组包含重复区域的点云数据,通过确定公共点之间的坐标变换参数转换至统一坐标系。
郑二龙等提出一种非迭代的求解七参数的方法,首先根据奇异值分解求出坐标转换矩阵,再根据最小二乘法,求解出3个平移参数和一个尺度参数 [1] 。曾文宪等提出了一种适用于任意旋转角的非线性模型 [2] 。陈义等提出以方向余弦为参数,构造旋转矩阵,然后对矩阵线性化,利用最小二乘迭代法,求解出转换参数 [3] 。
传统的七参数方法在用于旋转角很小的情况时,会忽略一些互乘项,旋转矩阵的元素由正弦函数和余弦函数组成,在面对小旋转角时会将正弦相似为0,余弦相似为1,相应的尺度参数和该部分互乘项之间的关系也被忽略,在面对大角度旋转角时,由于这些近似,求解的参数估值会产生偏差,甚至会导致失真。因此本文我们采用十三参数的模型,采取不求旋转角,求旋转矩阵的方法,将旋转矩阵的九个元素当作未知参数进行求解,可以解决任意旋转角的坐标转换。
2. 最小二乘理论
最小二乘原理及其最优化准则是求解参数最优估值过程中最常用的函数模型,最小二乘的函数模型和随机模型归纳为 [4] :
函数模型为:
(1)
随机模型:
(2)
式中,B为系数矩阵,X为待估的参数向量,L为实际观测向量,d为随机观测误差。D为d的协方差阵,Q为协因数阵,p为观测值权阵。 为单位权中误差。平差时,一般对参数X都取近似值 ,令
(3)
带入上式并令
(4)
上式中, 为观测方程的近似值,所以l是观测值与其近似值之差,由此可得误差方程为:
(5)
由最大似然估计求得的最小二乘最优平差准则为:
(6)
在该准则下,针对不同的问题,可以构建不同的平差方法。间接平差方法就是在该平差准则要求下常用的求解待定参数的方法。按照最小二乘原理,满足上式平差准则的要求。按照数学上求函数自由极值的方法可得间接平差的解法,可导出求解公式为:
(7)
3. 最小二乘的三维坐标转换通用模型
最小二乘(LS)是求解非线性方程的组的数学解法,在求解三维坐标转换参数中,将观测向量作为待估参数,三维坐标转换模型可描述为 [4] :
(8)
式中,n表示两点集中公共点个数, 表示 的元素为1的向量; 分别为源数据坐标系和目标数据坐标系下的公共点坐标; 为旋转矩阵。旋转矩阵为正交矩阵,应满足正交矩阵的条件 。
旋转矩阵 为 的乘积,其中 分别为:
在三维坐标转换模型中,七参数法是应用最广泛的。所谓七参数包括一个比例参数、坐标原点的三个平移参数以及三坐标轴旋转的三个角度值。七参数的坐标转换模型为:
(9)
当两个三维坐标系中,有三个或三个以上的同名点时,即可运用七参数法进行求解。但是七参数法在欧拉旋转角较小的情况下,不但进行了近似,而且还忽略了一些互乘项,近似化程度过高模型容易失真。在三维配准过程中,为实现任意角度的三维坐标配准,有人提出了在不求欧拉旋转角的情况下,求旋转矩阵 的方法,即把旋转矩阵的9个元素当作未知数进行求解。
即可得:
此时未知参数为 十三个参数。
对式(9)用Taylor级数展开将非线性七参数模型进行线性化。在参数初值 ,根据(9),令 得:
(10)
式中, 为平移参数改正数, 为尺度参数改正数, 为旋转矩阵的微分。当两数据点集中,有足够的对应控制点时(三个或者三个以上),根据式(10)就可构造三维坐标转换模型,并结合一定平差方法和最优准则进行求解计算得到参数的最佳估值。
4. 最小二乘的三维坐标转换模型的解法
上面介绍了基于最小二乘的三维坐标转换模型的建立,下面将推导该模型的解法。三维坐标转换的公式为 [5] :
(11)
式中, 为原坐标系下的坐标, 为目标坐标系下的坐标, 为平移参数,K为式(9)中k+1,R为旋转矩阵。
旋转矩阵为正交矩阵,应满足正交矩阵的条件 ,则旋转矩阵的九个元素满足下面的非线性条件:
(12)
从而,R矩阵中仅有三个独立参数,其他6个参数可以通过正交条件用三个独立参数表示。
在以往空间坐标系转换中,若有三个以上的公共控制点,应用最小二乘原理解算式(11)便可得到三个平移参数、三个旋转参数、一个尺度参数。但由于旋转矩阵中仅有三个独立参数,而其余六个是非线性函数,因此直接解算式(11)非常麻烦。因此将1个尺度参数、3个平移参数、9个方向余弦参数共13个参数设为位置参数。将式(11)用Taylor展开得:
(13)
其中:
则可以列出误差方程
(14)
式中:
(15)
则可以表示成间接平差的形式:
(16)
式中, ; 。
接着对6个正交约束条件进行线性化,并写为标准形式为:
(17)
式中:
附有限制条件的间接平差的数学模型为:
(18)
(19)
法方程为:
(20)
式中, ; ; ;
则得到其解为:
(21)
应用本方法进行坐标转换,可按以下步骤实现:
1) 近似值的确定。一般情况下,取
, ,
2) 按式(16)组成误差方程,若有n个点,则可有3n个误差方程;
3) 按式(17)组成约束条件方程。
4) 根据附有限制性条件的间接平差来求解参数的最新值,此时需要注意的是矩阵B的条件数非常大,在求逆时需要使用广义逆矩阵的方法求 。
5) 迭代的终止条件是上一次计算出来的参数与本次计算得到的参数之间的差值的绝对值小于10-6。根据参数的大小判断是否满足收敛要求,重复步骤2~4,直到满足收敛要求。
5. 实验分析
为验证附上述两节中三维坐标转换的模型和解法的可行性。本文结合MATLAB程序语言,利用三维激光扫描仪在常州地铁扫描的数据中的两站点云数据来演示点云坐标的配准过程:
1) 利用上述方法根据标靶球的坐标来求解转换参数。
转换参数结果如下:
Table 1. 1, 2 Station target ball coordinates
表1. 1、2测站标靶球坐标
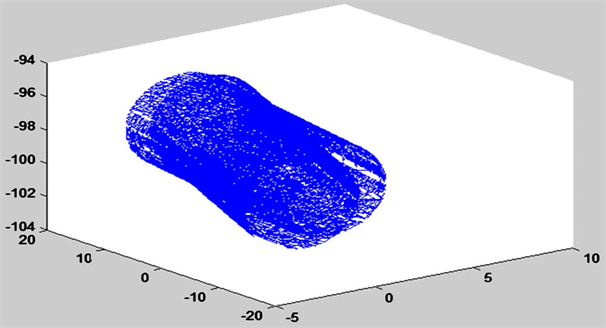
Figure 1. Unregistered point cloud
图1. 未配准点云图
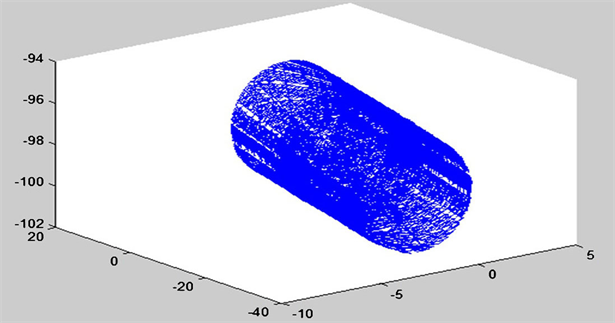
Figure 2. Two-site cloud with registration
图2. 配准完的两站点云
2) 利用上述求得的转换参数对两站的点云数据进行配准。源数据点和目标数据点坐标如表1所示,未配准点云如图1所示,配准完点云如图2所示。
6. 小结
在配准过程中,常用的七参数模型在面对小旋转角时会进行相似以及忽略一些互乘项,因此当旋转角为大旋转角时便会由于近似化程度过高使程序失真。本文采取在不求欧拉旋转角的情况下,求旋转矩阵的方法,即把旋转矩阵的9个元素当作未知数进行求解的十三参数的方法,该方法适用于求解任意旋转角的三维坐标转换,大大提高了该方法的适用性。
基金项目
地理国情监测国家测绘地理信息局重点实验室开放基金(项目编号:2016NGCM01)。
文章引用
陈坤,逯跃锋,楚潇蓉,陆黎娟. 基于最小二乘原理的点云数据配准
Point Cloud Data Registration Based on Least Squares[J]. 测绘科学技术, 2018, 06(03): 188-195. https://doi.org/10.12677/GST.2018.63021
参考文献
- 1. 郑二龙, 伍吉仓, 吕志鹏. 一种求解三维坐标转换参数的非迭代方法[J]. 测绘通报, 2014(8): 40-43.
- 2. 曾文宪, 陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报(信息科学版), 2003, 28(5): 566-568.
- 3. 陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报(信息科学版), 2004, 29(12): 1101-1105.
- 4. 刘亚彬. 基于总体最小二乘的点云三维配准及改进的ICP算法研究[D]: [硕士学位论文]. 徐州: 中国矿业大学, 2016.
- 5. 官云兰, 贾凤海. 地面三维激光扫描多站点云数据配准新方法[J]. 中国矿业大学学报, 2013, 42(5): 880-886.
NOTES
*通讯作者。
