Journal of Aerospace Science and Technology
Vol.05 No.03(2017), Article ID:22194,12
pages
10.12677/JAST.2017.53017
A Hybrid Optimization Method for Interplanetary Transition Trajectory Optimization
Mingying Huo, Naiming Qi, Shilei Cao, Yanmao Ye
Department of Aerospace and Mechanics Engineering, Harbin Institute of Technology, Harbin Heilongjiang

Received: Sep. 7th, 2017; accepted: Sep. 21st, 2017; published: Sep. 28th, 2017

ABSTRACT
In this paper, a hybrid genetic algorithm Gauss pseudospectral method is proposed for the interplanetary transition trajectory optimization. The initial guesses for the state and control histories used in the Gauss pseudospectral method are interpolated from the best solution of a genetic algorithm. The minimum-time low-thrust transfer trajectory from a geocentric circular orbit to an areocentric circular orbit was computed to verify the proposed hybrid optimization method. The numerical results show that the proposed hybrid approach effectively includes global search ability of genetic algorithm and the high convergence rate of sequential quadratic programming, and has the capability to search the feasible and global optimal solution without any initial value guess.
Keywords:Gauss Pseudospectral Method, Genetic Algorithm, Trajectory Optimization
一种用于行星间转移轨迹优化的混合优化方法
霍明英,齐乃明,曹世磊,叶炎茂
哈尔滨工业大学航空宇航与力学工程系,黑龙江 哈尔滨
收稿日期:2017年8月25日;录用日期:2017年9月7日;发布日期:2017年9月28日

摘 要
本文针对行星间转移轨迹优化问题,提出一种结合Gauss伪谱法和遗传算法的混合优化方法。这种混合优化方法通过遗传算法全局寻优获得Gauss伪谱法中所用的状态变量及控制变量初值,然后Gauss伪谱法根据遗传算法获得的初值进一步寻优,从而克服了传统间接优化法和直接优化法对初值的依赖。本文以地球至火星低推进过渡轨迹优化问题为例,对所提出的混合优化方法进行验证。仿真结果表明,这种优化方法既具有遗传算法的全局寻优能力又具有Gauss伪谱法的局部强收敛特性,能够在无任何初值猜测的情况下完成对近似全局最优解的搜索。
关键词 :Gausss伪谱法,遗传算法,轨迹优化

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
航天器轨迹优化是总体优化设计中的重要组成部分,在航天器设计状态基本已定的情况下,轨迹优化是提高航天任务及航天器性能为数不多的途径,在某种程度上也是唯一途径 [1] 。起初学者们都采用最优控制理论推导轨迹最优的解析解,如今归纳为解析法,该方法对于简单的线性系统比较有效,对于复杂非线性系统就显得力不从心 [2] 。得益于计算机技术的飞速发展,数值解法以其对复杂非线性系统的高效优化能力,近年来得到了国内外相关专家的关注。
就轨迹优化问题的转换方法为例,数值解法主要有直接法和间接法两类。间接法的基本原理是基于 Pontryagin极大值原理将最优控制问题转化为Hamilton边值问题,具有满足一阶最优条件且精度高等优点。但是由于间接法中的协态变量初值猜测困难且收敛半径小,限制了间接法的应用与发展。直接法通过把控制变量或状态变量离散化,将连续系统最优控制问题转换为一个非线性规划问题,再采用参数化优化方法求解使性能指标最优的参数,从而获得最优控制问题的解 [1] 。直接法避免了间接法对协态变量初值敏感的缺点,且可以有效处理约束条件,近几十年来得到快速的发展。
Gauss伪谱法由David Benson提出,作为直接优化方法中的一种,利用全局插值多项式的有限基来近似状态量和控制量,用Legendre-Gauss (LG)配点规则保证微分方程组满足约束条件,对多项式进行求导来近似动力学方程中的状态变量对时间的导数,从而将连续最优问题转化成非线性规划问题 [3] 。然后通过成熟的序列二次规划(SQP)方法对非线性规划问题求解。最近关于伪谱法的大量研究表明,伪谱法优化参数较少,计算精度较高,且满足一阶最优条件,实现了直接法与间接法的统一。理论上Gauss伪谱法可以直接应用于轨迹优化问题,但是当选取LG点较多时会出现初值赋值繁琐,且不合适的初值猜测会导致最终优化结果收敛到不可行解或局部最优解。而且Gauss伪谱法的最优求解策略为序列二次规划算法,这种算法局部搜索能力很强且效率较高,但是不具备对全局最优解的搜索能力,获得的解多为局部最优解。
针对Gauss伪谱法的上述问题,本文提出一种结合Gauss伪谱法和遗传算法的混合优化方法。这种混合优化方法的基本思想是首先通过较少的LG点对原问题进行离散化,然后通过遗传算法(GA)对最优解进行全局随机搜索,所得最优解经过插值后作为Gauss伪谱法较多LG点非线性规划问题的初值猜测,然后通过序列二次规划算法对最优解进行计算。这种优化方法有效地结合了遗传算法的全局随机搜索能力和序列二次规划算法的局部强搜索能力,能够在无任何初值猜测情况下完成对近似全局最优解的搜索。
本文以低推进飞行器从地球至火星过渡轨迹优化问题为例,验证所提出的混合优化算法。本文组织结构如下:第二节对地球至火星轨迹优化问题进行描述,第三节主要阐述混合优化算法的具体实施方法,第四节对仿真计算结果进行分析,第五节总结全文,得出结论。
2. 问题描述
为了验证所提出混合优化方法的性能,本文以Sean Tang描述的低推进飞行器地球至火星过渡轨迹优化问题 [4] 为例,采用混合优化方法对此问题进行优化,与Sean Tang采用Hermite-Legendre-Gauss- Lobatto配点法的优化结果进行对比。Sean Tang将上述优化问题分作三个阶段,即地球影响球逃离阶段、日心运动阶段和火星同步轨道抵达阶段(下文简称为地球中心段,太阳中心段和火星中心段),各阶段均为两体运动问题,中心引力天体分别为地球、太阳和火星,运动阶段划分示意图如图1所示。
2.1. 性能指标
低推进飞行器地球至火星过渡轨迹优化问题的优化性能指标为时间最优,即优化目标在最短的时间完成自地球同步轨道至火星同步轨道的过渡。由于将整个过渡过程分作地球中心段、太阳中心段和火星中心段三个阶段,本问题的优化性能指标可写做
(1)
其中
为飞行器脱离地球影响球所用时间; 为飞行器自地球公转轨道过渡至火星公转轨道所用时间;
为飞行器自火星影响球边界至火星同步轨道所用时间。
为飞行器自地球公转轨道过渡至火星公转轨道所用时间;
为飞行器自火星影响球边界至火星同步轨道所用时间。
2.2. 动力学方程
假设空间飞行器在地球中心段、太阳中心段和火星中心段中分别只受到地球的引力、太阳的引力和火星的引力。则通过图2可以得出,在地球中心极坐标系 下的低推进飞行器动力学方程如下:

Figure 1. Sketch map of motion phase division
图1. 运动阶段划分示意图

Figure 2. Space vehicle propulsion angle
图2. 空间飞行器推进角示意图
(2)
其中 为地球的引力常数; 为推力的指向角; 为推力产生的加速度大小; 为空间飞行器在地球中心极坐标系下的径向速度; 为空间飞行器在地球中心极坐标系下的切向速度。
同理,在太阳中心极坐标系 和火星中心极坐标系 下的动力学方程如式(3)和式(4)所示。
(3)
(4)
其中 为太阳引力常数; 为火星引力常数。
2.3. 边界约束
假设空间飞行器的起始轨道为地球同步轨道,则地球中心段轨迹优化初始状态为
(5)
其中 为地球的平均半径。
地球中心段的结束条件为空间飞行器抵达地球影响球边界,即
(6)
火星中心段起始于空间飞行器进入火星影响球,其初始状态为
(7)
其中 为火星的平均半径。
火星中心段的结束条件为空间飞行器抵达火星同步轨道,即
(8)
空间飞行器抵达地球影响边界后便进入太阳中心段,通过分析图3(a)中的几何关系,可得出地球中心段与太阳中心段之间的坐标转换方程。
 (9)
(9)
其中
为地球绕太阳转过的角度,在
时刻 ,
为地球的公转角速度。
,
为地球的公转角速度。
同理,通过分析图3(b)中的几何关系,可得出太阳中心段和火星中心段的坐标转换方程。
 (a)
(a) (b)
(b)
Figure 3. Coordinate system transformation. (a) Transformation from Geocentric to Heliocentric coordinate; (b) Transformation from Heliocentric to Mars coordinate
图3. 坐标系转换示意图。(a)地心–日心坐标转换示意图;(b)日心–火星坐标系转换示意图
(10)
其中 为火星绕太阳转过的角度,在 时刻 ; 为火星的公转角速度; 为任务初始时刻火星领先地球的角度,为与参考文献 [4] 中所描述的问题一致,取 。
3. 混合优化方法
从理论上分析,直接应用一般的Gauss伪谱法可以求解轨迹优化问题,然而在实际应用中却存在以下困难:1) 当选取配点较多时,设计变量数目会比较庞大,给定设计变量的工作会比较繁琐,且不恰当的初值会使问题收敛到不可行解。2) Gauss伪谱法将动力学方程转化为代数等式约束方程,当选取配点较多时,相应的代数约束方程将较多,在如此多约束条件下,很难直接快速地找到可行解 [1] 。
考虑到Gauss伪谱法应用于轨迹优化的问题,提出一种结合高斯伪谱法和遗传算法的混合优化方法。这种混合优化方法的基本思想是首先通过较少的LG点对原问题进行离散化,然后通过遗传算法对最优解进行全局随机搜索,所得最优解经过插值后作为Gauss伪谱法较多LG点非线性规划问题的初值猜测,然后通过序列二次规划算法对最优解进行计算,基于混合优化法的轨迹优化流程如图4所示。由于地球中心运动段、太阳中心运动段和火星运动中心段优化问题相似,因此本节以地球中心运动段轨迹优化问题为例,对所提出的混合优化方法进行阐述,太阳中心段和火星中心段优化轨迹生成方法与之相似。

Figure 4. Trajectory optimization process based on hybrid optimization method
图4. 基于混合优化方法的轨迹优化流程
3.1. 基于Gauss伪谱法的离散化
Gauss伪谱法的基本思想是用全局正交多项式对状态空间和控制空间进行逼近,将动力学微分约束转化成代数约束,从而可以用成熟的非线性规划方法求解最优控制问题 [5] 。Gauss伪谱法的配点选取 阶LG点,即 阶Legendre多项式的根。
最优控制问题的时间区间为 ,而采用Gauss伪谱法需要将时间区间转换到 区间内:
(11)
用N阶拉格朗日插值多项式对状态变量和控制变量进行拟合近似:
(12)
(13)
其中: 为 个LG点,均在 区间内, , 。
则状态变量和控制变量的微分可近似为:
(14)
其中
(15)
(16)
则将动力学微分约束转化成代数约束:
(17)
边界约束通过Gauss二次积分转化为:
(18)
由于本问题性能指标为Blaze型,不存在积分项,因此地球中心段优化性能指标函数为:
(19)
地球中心段动力学约束微分方程式(1)转化成的代数约束方程如式(20),离散后的边界约束方程如式(21),本问题离散后共 个代数约束方程。
(20)
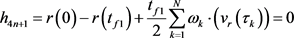 (21)
(21)
3.2. 基于遗传算法的初值估计
遗传算法作为一种主要用于计算离散优化问题近似解的工具,在连续优化问题中的应用并不是很具有吸引力。然而,由于遗传算法的无需初值计算能力和全局随机搜索能力使其非常适合于配点法和伪谱法的初值计算 [5] 。通过结合遗传算法全局随机搜索能力和序列二次规划算法强收敛能力,所提出的混合优化算法能够在无任何初值猜测的情况下完成对近似全局最优解的搜索。近年来,国内相关学者也基于现代寻优算法开展了空间飞行器轨迹优化研究 [6] [7] [8] [9] [10] 。
通常意义而言,遗传算法主要用于处理无约束非线性规划问题,然而实际问题中所要处理的问题经常是有约束非线性规划问题。本文通过应用罚函数法,将原约束问题转换成非约束问题。在地球中心段轨迹优化问题中,遗传算法优化性能指标为
(22)
其中 为罚因子。
3.3. 基于序列二次规划的最优解计算
最优解计算是以遗传算法计算结果作为非线性规划问题的初值进行寻优,性能指标为时间最优。本文中,最优解计算采用MATLAB优化工具箱中的fmincon函数,优化策略采用序列二次规划优化算法。最优解计算处理的非线性规划问题如下
(23)
4. 仿真计算及结果分析
本文将地球至火星过渡轨迹划分为三个阶段,即地球中心段、太阳中心段和火星中心段。本节基于所提出的混合优化方法对三段轨迹分别进行优化。为与Sean Tang的优化问题一致,本文的优化顺序如下:
1) 首先对地球中心段过渡轨迹进行正向轨迹优化,根据所得地球中心段终端状态通过坐标转换方程(9)得到太阳中心段始端状态;
2) 然后对火星中心段过渡轨迹进行反向轨迹优化,即以终端约束作为始端状态,以始端约束作为终端状态进行轨迹优化,根据所得火星中心段始端状态通过坐标转换方程(10)得到太阳中心段终端状态;
3) 最后根据所获得的始端状态和终端状态对太阳中心段过渡轨迹进行优化。
4.1. 地球中心段
在地球中心段轨迹优化过程中,初始解计算选取LG点个数为14,种群数量为100,最大迭代次数为200。最优解计算选取LG点个数为100,约束允许误差为 (TolCon)。地球中心段最优轨迹如图5所示,相对轨道半径–时间曲线、极角–时间曲线、径向速度–时间曲线、切向速度–时间曲线如图6所示。
4.2. 火星中心段
在火星中心段轨迹优化过程中,初始解计算选取LG点个数为14,种群数量为100,最大迭代次数为200。最优解计算选取LG点个数为80,约束允许误差为 (TolCon),火星中心段最优轨迹如图7所示。

Figure 5. Optimal trajectory in the geocentric section
图5. 地球中心段最优轨迹
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
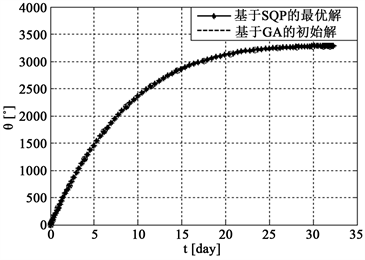
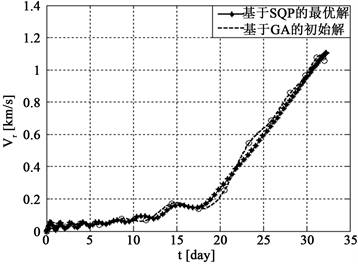
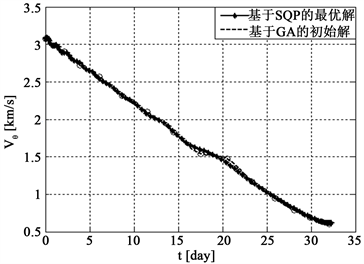
Figure 6. Curve of time-state variables in the geocentric section. (a) Curve of time-radius; (b) Curve of time-Polar; (c) Curve of time-Radial velocity; (d) Curve of time-Tangential velocity
图6. 地球中心段时间–状态变量曲线图。(a)时间–轨道半径曲线;(b)时间–极角曲线;(c)时间–径向速度曲线;(d)时间–切向速度曲线

Figure 7. Optimal trajectory in central section of mars
图7. 火星中心段最优轨迹
4.3. 太阳中心段
在太阳中心段轨迹优化过程中,初始解计算选取LG点个数为14,种群数量为100,最大迭代次数为200。最优解计算选取LG点个数为80,约束允许误差为 (TolCon),太阳中心段最优轨迹如图8所示。
(TolCon),太阳中心段最优轨迹如图8所示。
4.4. 结果分析
由仿真结果可以看出,基于遗传算法的初始解和基于序列二次规划的最优解均能很好地满足边界约束,且最优解与初始解的变化趋势是一致的。因此,遗传算法适用于Gauss伪谱法中非线性规划问题的初值估计,所提出的混合优化算法是合理的。
通过与Sean Tang提出的HLGL配点法优化结果进行对比,本文所提出的混合算法的优化结果与其十分常接近,且总飞行时间小于Sean Tang所采用的方法,如表1所示。由此可见,本文所提出的优化方法有效地结合了遗传算法的全局随机搜索能力和序列二次规划算法的局部强搜索能力,能够在无任何初值猜测情况下完成对近似全局最优解的搜索。
5. 结论
本文针对行星间转移轨迹优化问题,提出一种结合遗传算法和Gauss伪谱法的混合优化方法。并以文献 [4] 中描述的地球至火星转移轨迹优化问题为例,用所提出的混合优化方法对其进行优化。仿真结果表明,遗传算法适用于Gauss伪谱法中非线性规划问题的初值估计,且总飞行时间小于文献 [4] 中的飞行时间。另外,所采用的Gauss伪谱法采用全局插值多项式进行离散,相比于文献 [4] 中的配点法具有一定优越性。仿真结果验证了所提出的混合优化方法能够在无任何初值猜测的情况下完成对近似全局最优解的搜索。本文提出的混合优化方法为状态变量和控制变量初值猜测困难的优化问题提供了一种有效的优化策略。本文所提出的方法相比于文献 [4] 最突出的优点是能够在无任何初值猜测的情况下完成轨迹优化。

Figure 8. Optimal trajectory in the Heliocentric section
图8. 太阳中心段最优轨迹
Table 1. Performance indicators for each stage
表1. 各阶段性能指标表
基金项目
中国博士后科学基金资助(2017M611372),黑龙江省政府博士后基金资助(NO.LBH-Z16082),微小型航天器技术国防重点学科实验室开放基金资助(HIT.KLOF.MST.201607),上海航天科技创新基金资助(NO.SAST2016039)。
文章引用
霍明英,齐乃明,曹世磊,叶炎茂. 一种用于行星间转移轨迹优化的混合优化方法
A Hybrid Optimization Method for Interplanetary Transition Trajectory Optimization[J]. 国际航空航天科学, 2017, 05(03): 151-162. http://dx.doi.org/10.12677/JAST.2017.53017
参考文献 (References)
- 1. 唐国金, 罗亚中, 雍恩米. 航天器轨迹优化理论、方法及应用[M]. 北京: 科学出版社, 2011.
- 2. 陈功, 傅瑜, 郭继峰. 飞行器轨迹优化方法综述[J]. 飞行力学, 2011, 29(4): 1-5.
- 3. Benson, D. (2005) A Gauss Pseudospectral Transcription for Optimal Control. Massachusetts Institute of Technology, Cambridge.
- 4. Tang, S. and Conway, B.A. (1995) Optimization of Low-Thrust Interplanetary Trajectories Using Collocation and Nonlinear Programming. Journal of Guidance, Control, and Dynamics, 18, 599-604.
- 5. 顾晓婕, 王新民, 李俨. 基于多模型切换的多观测器轨迹优化研究[J]. 控制与决策, 2011, 26(6): 873-878.
- 6. 黄海滨, 马广富, 等. 基于伪谱法的编队卫星队形重构防碰撞轨迹优化[J]. 控制与决策, 2012, 27(4): 551-556.
- 7. 叶媛媛, 闵春平, 沈林成. 多UCAV 任务分配的混合遗传算法与约束处理[J]. 控制与决策, 2006, 21(7): 781-786.
- 8. Subbarao, K. and Shippey, B.M. (2009) Hybrid Genetic Algorithm Collocation Method for Trajectory Optimization. Journal of Guidance, Control, and Dynamics, 32, 1396-1403.
- 9. 韩敏, 王明慧, 范剑超. 基于改进差分进化算法的在线轨迹优化[J]. 控制与决策, 2012, 27(2): 247-251.
- 10. 何大阔, 王福利, 毛志忠. 离散非线性规划问题的改进遗传算法[J]. 控制与决策, 2006, 21(4): 396-399.
