辽宁师范大学数学学院，辽宁 大连

收稿日期：2021年12月26日；录用日期：2022年1月16日；发布日期：2022年1月28日

摘要

近年来，许多基于张量核范数的方法被提出解决张量填充的问题，并在图像和视频修复任务中受到了极大的关注。但是，核范数优化过程中会存在过度收缩问题。为了解决这个问题，通过可逆线性变换的张量积和张量奇异值分解，提出了基于张量分解的双核范数，证明了张量Schatten-p (p = 1/2)范数与张量双核范数的一致性，构造了双核范数正则化张量填充模型，并且通过交替方向乘子法求解优化模型。在合成数据和真实世界的数据集上的实验结果，可以看出所提出的算法比目前最优的张量填充方法更有效。

关键词

张量填充，张量分解，凸优化，交替方向乘子法

Robust Low-Rank Tensor Completion via Double Nuclear Norm Minimization

Jun Zhang, Zheng’er Li, Wei Jiang

School of Mathematics, Liaoning Normal University, Dalian Liaoning

Received: Dec. 26^th, 2021; accepted: Jan. 16^th, 2022; published: Jan. 28^th, 2022

ABSTRACT

Recently, methods based on tensor nuclear norm are proposed to address the issue of tensor completion, which have received great attention in the inpainting tasks of image and video. However, excessive shrinkage problem exists in the process of nuclear norm optimization. In order to solve this issue, with tensor-tensor product and tensor singular value decomposition based on inverse linear transforms, tensor double nuclear norm based on tensor factorization is defined. We also prove that it is equivalent to tensor Schatten-p (p = 1/2) norm and propose a double nuclear norm regularized tensor completion (DNTC) model. ADMM is used to solve this optimization model. It’s shown that the proposed method is more accurate and effective than the state-of-the-art methods for tensor completion through the experimental results on synthetic and real data sets.

Keywords:Tensor Completion, Tensor Factorization, Convex Optimization, Alternating Direction Method of Multipliers

Copyright © 2022 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

张量 [1] 作为向量和矩阵的高阶推广，是多维数据应用的表达方式。例如，彩色图像可以被视为具有行、列和色彩通道的三阶张量，而灰度视频是具有两个空间模式和一个时间模式的三阶张量。分析高阶张量数据直观方法是将其转换为矩阵，利用矩阵的性质对数据进行分析，但这种转换通常会导致信息丢失和性能下降。高维数据分析技术充分利用了张量的多线性结构，为张量数据提供了统一的理论框架，可以实现高效的分析效果。实际上，张量数据可能会部分丢失或被严重损坏，需要构造有效模型恢复部分丢失与损坏的数据，由此引入张量填充问题 [2]。

$\mathcal{T}\in {ℝ}^{n_1\times n_2\times n_3}$ 是三维观测张量， $\mathcal{X}\in {ℝ}^{n_1\times n_2\times n_3}$ 是恢复的低秩张量，张量填充的模型为：

$\underset{\mathcal{X}}{\min }\mathrm{rank}\left(\mathcal{X}\right)\text{s}\text{.t}\text{.}{\mathcal{P}}_{\Omega }\left(\mathcal{X}\right)={\mathcal{P}}_{\Omega }\left(\mathcal{T}\right)$ (1)

其中， $\mathrm{rank}\left(\mathcal{X}\right)$ 为 $\mathcal{X}$ 的秩函数， $\Omega \subseteq \left\{\left(i,j,k\right)|i\in \left\{1,2,\cdots ,n_1\right\},j\in \left\{1,2,\cdots ,n_2\right\},k\in \left\{1,2,\cdots ,n_3\right\}\right\}$ 是 $\mathcal{T}$ 的已知元素相对应的索引集， ${\mathcal{P}}_{\Omega }(\cdot )$ 为采样算子，定义为

${\mathcal{P}}_{\Omega }\left(\mathcal{X}\right)=\{\begin{array}{l}{\mathcal{X}}_{ijk},\text{if}\left(i,j,k\right)\in \Omega \hfill \\ 0,\text{otherwise}.\hfill \end{array}$ (2)

基于不同的张量分解，定义不同张量秩，比如基于CANDECOMP/PARAFAC分解的CP秩 [3]，基于Tucker分解 [4] 的Tucker秩，基于Tensor-Train分解 [5] 的TT秩，和基于张量奇异值分解的tubal秩 [6]。

CP秩定义为秩1张量分解的最小数量，其计算通常为NP-hard问题 [7]。张量Tucker秩是一个向量，其元素分别是沿着每种模展开矩阵的秩 [2]。TT秩是由均衡矩阵形成的矩阵的秩组成，即沿着模排列对张量进行矩阵化 [8]。近年来，通过对三阶张量进行傅里叶变换产生的张量积 [9]，基于张量奇异值分解 [6]，诱导出张量tubal秩 [10] [11]。张量tubal秩是张量中非零对角管(tubes)的个数。

直接最小化秩函数通常是NP-hard问题，基于张量秩的不同定义，提出了各种张量核范数作为张量秩替代。Friedland等 [10] 将张量核范数定义为CP秩的凸包络，但很难测量相对于CP秩的紧度。为了解决这个问题，刘等 [2] 给出了一种张量核范数定义为模展开矩阵核范数的和(Sum of Nuclear Norms, SNN)作为Tucker秩的凸包络。但是，SNN将高阶张量展开为矩阵，从而破坏了张量数据的内部结构。为了保持张量的结构，Semerci等人 [12]，在傅立叶域中基于张量tubal秩，提出了一种新的张量核范数(Tensor Nuclear Norm, TNN)。随后，张等 [12] 人将TNN应用于张量填充，并获得了较好的图像与视频恢复效果。

尽管TNN具有完美的数学理论支撑，但是存在两个问题。首先，作为张量tubal秩的凸松弛，在优化TNN的过程中，对不同的奇异值减去相同域值，从而导致了等距收缩问题。其次，对高维张量数据进行奇异值分解，计算代价太高。使用非凸函数代替核范数作为秩函数的松弛，可以避免等距收缩问题。张量分解的方法，可以有效地降低计算复杂度。基于这两种思想，我们提出了基于双核范数最小化的低秩张量填充。首先给出张量双核范数的定义，然后证明张量双核范数等价于具体的张量Schatten-p (p = 1/2)范数 [13]。采用两个小的张量张量积表示原张量，从而避免解大张量奇异值问题。基于张量分解的思想，给出了相应的凸替换，将非凸问题转换为凸问题。由于对小张量进行奇异值分解，模型的计算复杂度会大大减少，并且每个子问题都有一个闭式解。

2. 张量基础

为了方便起见，用粗体小写字母粗体 $a$，粗体大写字母 $A$ 与粗体手写体字母 $\mathcal{A}$ 表示标量，矩阵和张量。对于 $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$，第 $\left(i,j,k\right)$ 个位置上的元素表示为 $\mathcal{A}\left(i,j,k\right)$ 或 ${\mathcal{A}}_{ijk}$，第i个水平切片、侧面切片与正面切片分别表示为 $\mathcal{A}\left(i,:,:\right)$，$\mathcal{A}\left(:,i,:\right)$ 和 $\mathcal{A}\left(:,:,i\right)$，特别地，用 ${\mathcal{A}}^{\left(i\right)}$ 表示第i个正面切片。第 $\left(i,j\right)$ 个管可以用 $\mathcal{A}\left(i,j,:\right)$ 表示，它实际上是一个长度为 $n_3$ 的向量。张量Frobenius范数定义为 ${\Vert \mathcal{A}\Vert }_F=\sqrt{{\displaystyle {\sum }_{ijk}{\Vert {\mathcal{A}}_{ijk}\Vert }^2}}$。令 $L:{ℝ}^{n_1\times n_2\times n_3}\to {ℝ}^{n_1\times n_2\times n_3}$ 是张量空间上的任意可逆线性变换，对 $\mathcal{A}$ 的每一个管纤维进行变换，可以得到 $\bar{\mathcal{A}}=L\left(\mathcal{A}\right)$，基于可逆线性变换，给出块对角矩阵和块循环矩阵的定义：

$\bar{A}=\mathrm{bdiag}\left(\bar{\mathcal{A}}\right)=\left[\begin{array}{cccc}{\bar{A}}^{\left(1\right)}& & & \\ & {\bar{A}}^{\left(2\right)}& & \\ & & \ddots & \\ & & & {\bar{A}}^{\left(n_3\right)}\end{array}\right]$,$\mathrm{bcirc}\left(\mathcal{A}\right)=\left[\begin{array}{cccc}{A}^{\left(1\right)}& A^{\left(n_3\right)}& \cdots & A^{\left(2\right)}\\ A^{\left(2\right)}& A^{\left(1\right)}& \cdots & A^{\left(3\right)}\\ ⋮& ⋮& \ddots & ⋮\\ A^{\left(n_3\right)}& A^{\left(n_3-1\right)}& \cdots & A^{\left(1\right)}\end{array}\right]$ (3)

此外，张量的展开、折叠算子定义如下：

$\mathrm{unfold}\left(\mathcal{A}\right)=\left[\begin{array}{c}{A}^{\left(1\right)}\\ A^{\left(2\right)}\\ ⋮\\ A^{\left(n_3\right)}\end{array}\right]$,$\mathrm{fold}\left(\mathrm{unfold}\left(\mathcal{A}\right)\right)=\mathcal{A}$ (4)

根据以上定义，给出张量核范数与张量tubal秩的定义。

定义1.1. (张量积) [10]：假设L是任意可逆线性变换， $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$，$\mathcal{B}\in {ℝ}^{n_2\times n_4\times n_3}$，则基于L的张量积定义为 $\mathcal{A}{\ast }_L\mathcal{B}=\mathrm{fold}\left(\text{bcirc}\left(\mathcal{A}\right)\cdot \mathrm{unfold}\left(\mathcal{B}\right)\right)$。

定义1.2. (张量转置) [10]：假设L是任意可逆线性变换， $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$，则 $\mathcal{A}$ 的转置 ${\mathcal{A}}^{\top }$ 定义为 $L{\left({\mathcal{A}}^{\top }\right)}^{\left(i\right)}={\left(L{\left(\mathcal{A}\right)}^{\left(i\right)}\right)}^{\top },i=1,\cdots ,n_3$。

定义1.3. (单位张量) [10]：假设L是任意可逆线性变换， $\mathcal{I}\in {ℝ}^{n_1\times n_2\times n_3}$，若 $L\left(\mathcal{I}\right)$ 的每一个正面切片都是 $n\times n$ 的单位矩阵，则 $\mathcal{I}$ 为单位张量。

定义1.4. (正交张量) [10]：假设L是任意可逆线性变换， $\mathcal{Q}\in {ℝ}^{n_1\times n_2\times n_3}$，如果满足 ${\mathcal{Q}}^{\top }{\ast }_L\mathcal{Q}=\mathcal{Q}{\ast }_L{\mathcal{Q}}^{\top }=\mathcal{I}$，则 $\mathcal{Q}$ 为正交张量。

定义1.5. (F-对角张量) [10]：假设L是任意可逆线性变换， $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$，若 $L\left(\mathcal{A}\right)$ 的每一个正面切片都是对角矩阵，则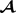为F-对角张量。

定理1.1. (张量奇异值分解) [10]：假设L是任意可逆线性变换， $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$，则 $\mathcal{A}$ 可以分解成 $\mathcal{A}=\mathcal{U}{\ast }_L\mathcal{S}{\ast }_L{\mathcal{V}}^{\top }$，其中 $\mathcal{U}{\ast }_L{\mathcal{U}}^{\top }=\mathcal{I}$，$\mathcal{V}{\ast }_L{\mathcal{V}}^{\top }=\mathcal{I}$ 且 $\mathcal{S}\in {ℝ}^{n_2\times n_2\times n_3}$ 是F-对角张量。

定义1.6. (张量multi秩、tubal秩) [10]：假设L是任意可逆线性变换，满足 $L^{\top }L=L{L}^{\top }=\mathcal{l}{I}_{n_3}$ 且 $\mathcal{l}>0$，给定 $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$，将其奇异值分解 $\mathcal{A}=\mathcal{U}{\ast }_L\mathcal{S}{\ast }_L{\mathcal{V}}^{\top }$，则张量multi秩定义为

$\text{ran}{\text{k}}_{\text{m}}\left(\mathcal{A}\right)=\left(\text{rank}{\left(\bar{A}\right)}^{\left(1\right)},\cdots ,\text{rank}{\left(\bar{A}\right)}^{\left(n_3\right)}\right)$ (5)

张量tubal秩定义为 $\mathcal{S}$ 的非零奇异管的数量，即

${\text{rank}}_{\text{t}}\left(\mathcal{A}\right)=\#\left\{i,\mathcal{S}\left(i,i,:\right)\ne 0\right\}=\#\left\{i,\mathcal{S}\left(i,i,1\right)\ne 0\right\}$ (6)

定义1.7. (张量核范数) [10]：假设L是任意可逆线性变换， $\mathcal{A}\in {ℝ}^{n_1\times n_2\times n_3}$，将其进奇异值分解 $\mathcal{A}=\mathcal{U}{\ast }_L\mathcal{S}{\ast }_L{\mathcal{V}}^{\top }$，则张量核范数定义为 ${\Vert \mathcal{A}\Vert }_{*}=\langle \mathcal{S},\mathcal{I}\rangle ={\displaystyle \underset{i=1}{\overset{r}{\sum }}\mathcal{S}\left(i,i,1\right)}$，其中r为 $\mathcal{A}$ 的tubal秩。

定理1.2. (张量奇异值阈值算子) [11]：对于任意 $\tau >0$，给定 $\mathcal{Y}\in {ℝ}^{n_1\times n_2\times n_3}$，则

$\underset{\mathcal{X}}{\min }\tau {\Vert \mathcal{X}\Vert }_{*}+\frac{1}{2}{\Vert \mathcal{X}-\mathcal{Y}\Vert }_F^2$ (7)

的解为 ${\mathcal{D}}_{\tau }\left(\mathcal{Y}\right)=\mathcal{U}{\ast }_L{\mathcal{S}}_{\tau }{\ast }_L{\mathcal{V}}^{\top }$，其中 ${\mathcal{S}}_{\tau }=L^{-1}\left({\left(\bar{\mathcal{S}}-\tau \right)}_{+}\right)$ 且 $t_{+}=\max \left(t,0\right)$。

3. 基于张量双核范数最小化的低秩张量填充

3.1. 双核范数

定义2.1：对于任意的张量 $\mathcal{X}\in {ℝ}^{n_1\times n_2\times n_3}$，其tubal秩 ${\text{rank}}_{\text{t}}\left(\mathcal{X}\right)\le r$。 $\mathcal{X}$ 可以被分解为两个张量的乘积，即 $\mathcal{X}=\mathcal{U}{\ast }_L{\mathcal{V}}^{\top }$，其中 $\mathcal{U}\in {ℝ}^{n_1\times r\times n_3}$，$\mathcal{V}\in {ℝ}^{n_2\times r\times n_3}$ 且 $\text{ran}{\text{k}}_{\text{t}}\left(\mathcal{U}\right)=\text{ran}{\text{k}}_{\text{t}}\left(\mathcal{V}\right)=r$。则张量双核范数定义为

${\Vert \mathcal{X}\Vert }_{TDN}=\underset{\mathcal{X}=\mathcal{U}{\ast }_L{\mathcal{V}}^{\top }}{\min }\frac{1}{4}{\left({\Vert \mathcal{U}\Vert }_{*}+{\Vert \mathcal{V}\Vert }_{*}\right)}^2$ (8)

定理2.1：给定 $\mathcal{U}\in {ℝ}^{n_1\times r\times n_3}$，$\mathcal{V}\in {ℝ}^{n_2\times r\times n_3}$，$\mathcal{X}\in {ℝ}^{n_1\times n_2\times n_3}$，满足 $\mathcal{X}=\mathcal{U}{\ast }_L{\mathcal{V}}^{\top }$ 且 $\text{ran}{\text{k}}_{\text{t}}\left(\mathcal{X}\right)\le r$，则有

${\Vert \mathcal{X}\Vert }_{\text{TDN}}={\Vert \mathcal{X}\Vert }_{{\mathcal{S}}_{1/2}}$ (9)

其中， ${\Vert \cdot \Vert }_{\text{TDN}}$ 表示张量双核范数， ${\Vert \cdot \Vert }_{{\mathcal{S}}_{1/2}}$ 表示张量Schatten-p范数。

3.2. 模型建立与求解

基于Schatten-p范数最小化的框架，张量双核范数正则化张量填充模型表示如下：

$\underset{\mathcal{U},\mathcal{V},\mathcal{X}}{\min }\frac{1}{2}\left({\Vert \mathcal{U}\Vert }_{*}+{\Vert \mathcal{V}\Vert }_{*}\right)+\frac{1}{2}\lambda {\Vert {\mathcal{P}}_{\Omega }\left(\mathcal{X}-\mathcal{T}\right)\Vert }_F^2,\text{s}\text{.t}.\text{}\mathcal{X}=\mathcal{U}{\ast }_L{\mathcal{V}}^{\top }$ (10)

为了求解优化(13)，使用交替方向乘子法，引入辅助变量 $\hat{\mathcal{U}}$ 与 $\hat{\mathcal{V}}$，优化以下式子：

$\underset{\mathcal{U},\mathcal{V},\mathcal{X}}{\min }\frac{1}{2}\left({\Vert \hat{\mathcal{U}}\Vert }_{*}+{\Vert \hat{\mathcal{V}}\Vert }_{*}\right)+\frac{\lambda }{2}{\Vert {\mathcal{P}}_{\Omega }\left(\mathcal{X}-\mathcal{T}\right)\Vert }_F^2,\text{s}\text{.t}.\mathcal{X}=\mathcal{U}{\ast }_L{\mathcal{V}}^{\top },\hat{\mathcal{U}}=\mathcal{U},\mathcal{V}=\mathcal{V}$ (11)

增广拉格朗日函数为：

$\begin{array}{l}{\mathcal{L}}_{\mu }\left(\mathcal{U},\mathcal{V},\mathcal{X},\hat{\mathcal{U}},\hat{\mathcal{V}},\left\{{\mathcal{Y}}_i\right\}\right)\\ =\frac{1}{2}\left({\Vert \hat{\mathcal{U}}\Vert }_{*}+{\Vert \hat{\mathcal{V}}\Vert }_{*}\right)+\frac{\lambda }{2}{\Vert {\mathcal{P}}_{\Omega }\left(\mathcal{X}-\mathcal{T}\right)\Vert }_F^2+\langle {\mathcal{Y}}_1,\mathcal{U}-\hat{\mathcal{U}}\rangle +\langle {\mathcal{Y}}_2,\mathcal{V}-\hat{\mathcal{V}}\rangle \\ +\langle {\mathcal{Y}}_3,\mathcal{X}-\mathcal{U}{\ast }_L{\mathcal{V}}^{\top }\rangle +\frac{\mu }{2}\left({\Vert \mathcal{U}-\hat{\mathcal{U}}\Vert }_F^2+{\Vert \mathcal{V}-\hat{\mathcal{V}}\Vert }_F^2+{\Vert \mathcal{X}-\mathcal{U}{\ast }_L{\mathcal{V}}^{\top }\Vert }_F^2\right)\end{array}$ (12)

其中， ${\mathcal{Y}}_1$，${\mathcal{Y}}_2$ 与 ${\mathcal{Y}}_3$ 是拉格朗日乘子张量， $\mu >0$ 是惩罚参数。使用交替方向乘子法更新。

1) 固定 ${\mathcal{V}}_k$ 、 ${\hat{\mathcal{U}}}_k$ 、 ${\hat{\mathcal{V}}}_k$ 、 ${\mathcal{X}}_k$ 、 ${\mathcal{Y}}_1^k$ 、 ${\mathcal{Y}}_2^k$ 、 ${\mathcal{Y}}_3^k$，更新 ${\mathcal{U}}_{k+1}$ ：

$\begin{array}{c}{\mathcal{U}}_{k+1}=\underset{\mathcal{U}}{\arg \min }\langle {\mathcal{Y}}_1^k,\mathcal{U}-{\hat{\mathcal{U}}}_k\rangle +\langle {\mathcal{Y}}_3,{\mathcal{X}}_k-\mathcal{U}{\ast }_L{\mathcal{V}}_k^{\top }\rangle \\ +\frac{{\mu }_k}{2}\left({\Vert \mathcal{U}-{\hat{\mathcal{U}}}_k\Vert }_F^2+{\Vert {\mathcal{X}}_k-\mathcal{U}{\ast }_L{\mathcal{V}}_k^{\top }\Vert }_F^2\right)\end{array}$ (13)

令(16)对 $\mathcal{U}$ 求偏导并将等于0，则有

${\mathcal{U}}_{k+1}=\left({\mu }_k{\hat{\mathcal{U}}}_k-{\mathcal{Y}}_1^k+\mathcal{G}{\ast }_L{\mathcal{V}}_k\right){\left({\mu }_k\mathcal{I}+\mu {\mathcal{V}}_k^{\top }{\ast }_L{\mathcal{V}}_k\right)}^{-1}$ (14)

其中， $\mathcal{G}={\mu }_k{\mathcal{X}}_k+{\mathcal{Y}}_3^k$。

2) 固定 ${\mathcal{U}}_{k+1}$ 、 ${\hat{\mathcal{U}}}_k$ 、 ${\hat{\mathcal{V}}}_k$ 、 ${\mathcal{X}}_k$ 、 ${\mathcal{Y}}_1^k$ 、 ${\mathcal{Y}}_2^k$ 、 ${\mathcal{Y}}_3^k$，更新 ${\mathcal{V}}_{k+1}$，同理，有

$\begin{array}{c}{\mathcal{V}}_{k+1}=\underset{\mathcal{V}}{\arg \min }\langle {\mathcal{Y}}_2^k,\mathcal{V}-{\hat{\mathcal{V}}}_k\rangle +\langle {\mathcal{U}}_{k+1}{\ast }_L{\mathcal{V}}^{\top }-{\mathcal{X}}_k,{\mathcal{Y}}_3^k\rangle \\ +\frac{{\mu }_k}{2}\left({\Vert \mathcal{V}-{\hat{\mathcal{V}}}_k\Vert }_F^2+{\Vert {\mathcal{X}}_k-{\mathcal{U}}_{k+1}{\ast }_L{\mathcal{V}}^{\top }\Vert }_F^2\right)\end{array}$ (15)

对 $\mathcal{V}$ 进行求偏导且为0，可得，

${\mathcal{V}}_{k+1}=\left({\mu }_k{\hat{\mathcal{V}}}_k-{\mathcal{Y}}_2^k+\mathcal{G}{\ast }_L{\mathcal{U}}_{k+1}\right){\left({\mu }_k\mathcal{I}+{\mu }_k{\mathcal{U}}_{k+1}^{\top }{\ast }_L{\mathcal{U}}_{k+1}\right)}^{-1}$ (16)

其中， $\mathcal{G}=\mu \mathcal{X}+{\mathcal{Y}}_3$.

3) 固定 ${\mathcal{U}}_{k+1}$ 、 ${\mathcal{V}}_{k+1}$ 、 ${\hat{\mathcal{V}}}_k$ 、 ${\mathcal{X}}_k$ 、 ${\mathcal{Y}}_1^k$ 、 ${\mathcal{Y}}_2^k$ 、 ${\mathcal{Y}}_3^k$，更新 ${\hat{\mathcal{U}}}_{k+1}$，有

$\begin{array}{c}{\hat{\mathcal{U}}}_{k+1}=\underset{\hat{\mathcal{U}}}{\arg \min }\frac{1}{2}{\Vert \hat{\mathcal{U}}\Vert }_{*}+\langle {\mathcal{Y}}_1^k,{\mathcal{U}}_{k+1}-\hat{\mathcal{U}}\rangle +\frac{{\mu }_k}{2}{\Vert {\mathcal{U}}_{k+1}-\hat{\mathcal{U}}\Vert }_F^2\\ =\underset{\hat{\mathcal{U}}}{\arg \min }\frac{1}{2}{\Vert \hat{\mathcal{U}}\Vert }_{*}+\frac{{\mu }_k}{2}{\Vert \hat{\mathcal{U}}-\left({\mathcal{U}}_{k+1}+{\mu }_k^{-1}{\mathcal{Y}}_1^k\right)\Vert }_F^2\\ ={\mathcal{D}}_{\frac{1}{2{\mu }_k}}\left({\mathcal{U}}_{k+1}+{\mu }_k^{-1}{\mathcal{Y}}_1^k\right)\end{array}$ (17)

4) 固定 ${\mathcal{U}}_{k+1}$ 、 ${\mathcal{V}}_{k+1}$ 、 ${\hat{\mathcal{U}}}_{k+1}$ 、 ${\mathcal{X}}_k$ 、 ${\mathcal{Y}}_1^k$ 、 ${\mathcal{Y}}_2^k$ 、 ${\mathcal{Y}}_3^k$，更新 ${\hat{\mathcal{V}}}_{k+1}$，有

$\begin{array}{c}{\hat{\mathcal{V}}}_{k+1}=\underset{\hat{\mathcal{V}}}{\arg \min }\frac{1}{2}{\Vert \hat{\mathcal{V}}\Vert }_{*}+\langle {\mathcal{Y}}_2^k,{\mathcal{V}}_{k+1}-\hat{\mathcal{V}}\rangle +\frac{{\mu }_k}{2}{\Vert {\mathcal{V}}_{k+1}-\hat{\mathcal{V}}\Vert }_F^2\\ =\underset{\hat{\mathcal{V}}}{\arg \min }\frac{1}{2}{\Vert \hat{\mathcal{V}}\Vert }_{*}+\frac{{\mu }_k}{2}{\Vert \hat{\mathcal{V}}-\left({\mathcal{V}}_{k+1}+{\mu }_k^{-1}{\mathcal{Y}}_2^k\right)\Vert }_F^2\\ ={\mathcal{D}}_{\frac{1}{2{\mu }_k}}\left({\mathcal{V}}_{k+1}+{\mu }_k^{-1}{\mathcal{Y}}_2^k\right)\end{array}$ (18)

5) 固定 ${\mathcal{U}}_{k+1}$ 、 ${\mathcal{V}}_{k+1}$ 、 ${\hat{\mathcal{U}}}_{k+1}$ 、 ${\hat{\mathcal{V}}}_{k+1}$ 、 ${\mathcal{Y}}_1^k$ 、 ${\mathcal{Y}}_2^k$ 、 ${\mathcal{Y}}_3^k$，更新 ${\mathcal{X}}_{k+1}$，有

$\begin{array}{c}\mathcal{X}=\underset{\mathcal{X}}{\arg \min }\frac{\lambda }{2}{\Vert {\mathcal{P}}_{\Omega }\left(\mathcal{X}-\mathcal{T}\right)\Vert }_F^2+\langle {\mathcal{Y}}_3^k,\mathcal{X}-{\mathcal{U}}_{k+1}{\ast }_L{\mathcal{V}}_{k+1}^{\top }\rangle +\frac{{\mu }_k}{2}{\Vert \mathcal{X}-{\mathcal{U}}_{k+1}{\ast }_L{\mathcal{V}}_{k+1}^{\top }\Vert }_F^2\\ =\underset{\mathcal{X}}{\arg \min }{\Vert {\mathcal{P}}_{\Omega }\left(\mathcal{X}-\mathcal{T}\right)\Vert }_F^2+\frac{{\mu }_k}{\lambda }{\Vert \mathcal{X}-\left({\mathcal{U}}_{k+1}{\ast }_L{\mathcal{V}}_{k+1}^{\top }\text{}-\text{}{\mu }_k^{-1}{\mathcal{Y}}_3^k\right)\Vert }_F^2\\ ={\mathcal{U}}_{k+1}{\ast }_L{\mathcal{V}}_{k+1}^{\top }\text{}+{\mu }_k^{-1}{\mathcal{Y}}_3^k+P_{\Omega }\left(\frac{\lambda \mathcal{T}+{\mu }_k{\mathcal{U}}_{k+1}{\ast }_L{\mathcal{V}}_{k+1}^{\top }\text{}-{\mathcal{Y}}_3^k}{\lambda +{\mu }_k}\right)\end{array}$ (19)

6) 固定 ${\mathcal{U}}_{k+1}$ 、 ${\mathcal{V}}_{k+1}$ 、 ${\hat{\mathcal{U}}}_{k+1}$ 、 ${\hat{\mathcal{V}}}_{k+1}$ 、 ${\mathcal{X}}_{k+1}$ 、 ${\mathcal{Y}}_2^k$ 、 ${\mathcal{Y}}_3^k$，更新 ${\mathcal{Y}}_1^{k+1}$，有

${\mathcal{Y}}_1^{k+1}={\mathcal{Y}}_1^k+{\mu }_k\left({\mathcal{U}}_{k+1}-{\hat{\mathcal{U}}}_{k+1}\right)$ (20)

7) 固定 ${\mathcal{U}}_{k+1}$ 、 ${\mathcal{V}}_{k+1}$ 、 ${\hat{\mathcal{U}}}_{k+1}$ 、 ${\hat{\mathcal{V}}}_{k+1}$ 、 ${\mathcal{X}}_{k+1}$ 、 ${\mathcal{Y}}_1^{k+1}$ 、 ${\mathcal{Y}}_3^k$，更新 ${\mathcal{Y}}_2^{k+1}$，有

${\mathcal{Y}}_2^{k+1}={\mathcal{Y}}_2^k+{\mu }_k\left({\mathcal{V}}_{k+1}-{\hat{\mathcal{V}}}_{k+1}\right)$ (21)

8) 固定 ${\mathcal{U}}_{k+1}$ 、 ${\mathcal{V}}_{k+1}$ 、 ${\hat{\mathcal{U}}}_{k+1}$ 、 ${\hat{\mathcal{V}}}_{k+1}$ 、 ${\mathcal{X}}_{k+1}$ 、 ${\mathcal{Y}}_1^{k+1}$ 、 ${\mathcal{Y}}_2^{k+1}$，更新 ${\mathcal{Y}}_3^{k+1}$，即

${\mathcal{Y}}_3^{k+1}={\mathcal{Y}}_3^k+{\mu }_k\left({\mathcal{X}}_{k+1}-{\mathcal{U}}_{k+1}{\ast }_L{\mathcal{V}}_{k+1}^{\top }\right)$ (22)

9) 更新参数 ${\mu }_k$

${\mu }_{k+1}=\rho {\mu }_k$ (23)

4. 实验

4.1. 合成数据

随机生成张量 $\mathcal{U}\in {ℝ}^{n_1\times r\times n_3}$ 与 $\mathcal{V}\in {ℝ}^{n_2\times r\times n_3}$，其中 $\mathcal{U}$ 与 $\mathcal{V}$ 的元素是从标准高斯分布中独立采样的。通过张量积 $\mathcal{U}{\ast }_L\mathcal{V}$，构建出tubal秩为r的张量 $\mathcal{X}\in {ℝ}^{n_1\times n_2\times n_3}$。随机选取 $\mathcal{X}$ 的 $p{n}_1{n}_2{n}_3$ 个位置构建相对应的索引集 $\Omega$，其中p为观测率。因此，合成数据构建方式如下，

$\mathcal{T}=\mathcal{X}+\sigma \mathcal{Z},{\mathcal{T}}_{ijk}={\mathcal{X}}_{ijk}+\sigma {\mathcal{Z}}_{ijk},\left(i,j,k\right)\in \Omega$ (24)

其中， $\mathcal{Z}$ 为均值为0，方差为1的高斯白噪声。

考虑三种可逆线性变换：1) 离散傅里叶变换(Discrete Fourier Transform, DFT)；2) 离散余弦变换(Discrete Cosine Transform, DCT)；3) 正交变换(Random Orthogonal Transform, ROM)。假设 $n_1=n_2=n_3=50$，正则化参数设为 $1/\left(2\sqrt{\max \left(n_1,n_2\right)}\right)$。采用相对均方误差测量结果，即

$\text{RSE}=\frac{{\Vert \hat{\mathcal{X}}-\mathcal{X}\Vert }_F}{{\Vert \mathcal{X}\Vert }_F}$ (25)

若 $\text{RSE}\le {10}^{-3}$，则可认为精确恢复。从表1的实验结果可以看出，在三种可逆线性变换的条件下，RSE远远小于10⁻³。因此，在不同的采样率与可逆线性变换下，部分观测张量可以精确恢复出来。这表明了基于任何可逆线性变换的DNTC是可行的、鲁棒的。

表1. 在不同线性变换下的随机数据填充的RSE结果

4.2. 图像修复

在图像修复任务中，选取ZJU数据集中4张图像，用TNN [11]、TCTF [14] 与DNTC三种方法进行对比，将峰值信噪比(Peak Signal to Noise Ratio, PSNR)、结构相似性(Structured Similarity Index, SSIM)与时间作为评价指标。实验中，观测率设置为0.4。图1为观测率0.4下的图像修复结果对比，表2给出了PSNR、SSIM与时间指标的直观对比结果。

表2. 自然图像上PSNR、SSIM与时间的性能对比

图1. 不同方法在4个图像上修复结果

从图1结果可以看出，在观测率为0.4的情况下，DNTC在3种可逆变换下的视觉效果差别不太明显，均比TNN与TCTF更好得刻画出细节部分。从表2可以看出，在峰值信噪比，基于任意线性变换的DNTC平均比TNN结果提升2 dB以上、比TCTF平均提升5 dB；在结构相似比方面，DNTC均高于TNN与TCTF，且最低提升0.02，原因是本文提出的双核范数比核范数更逼近张量的tubal秩，避免了等距收缩问题。

除此之外，DNTC的运行时间明显低于TNN的时间，主要原因是DNTC采取了张量分解的方法，对两个小的张量进行优化，从而降低了计算复杂度。与另一个张量分解方法TCTF相比，DNTC在DFT与DCT下与TCTF的时间结果较为相似，甚至更快。在ROM下少慢于TCTF。主要是由于TCTF只是用Frobenius范数作为正则化项，不需要张量奇异值分解，计算复杂度较低，但该方法不能很好的刻画张量的线性结构，因此PSNR数值最低。而在ROM下，DNTC没有快速算法，导致了计算复杂度高于TCTF。

5. 结束语

针对张量填充问题，结合了Schatten-p范数与张量分解的思想，提出了基于双核范数最小化方法，保证了张量填充的效果优越性，并提高了优化速度。在后续工作中，将双核范数扩展到张量低秩表示模型中，以利于子空间聚类。

文章引用

张 军,李峥儿,姜 伟. 基于双核范数最小化的低秩张量填充
Robust Low-Rank Tensor Completion via Double Nuclear Norm Minimization[J]. 应用数学进展, 2022, 11(01): 442-449. https://doi.org/10.12677/AAM.2022.111052

参考文献