Modeling and Simulation
Vol.
12
No.
03
(
2023
), Article ID:
65594
,
17
pages
10.12677/MOS.2023.123217
基于动静态刚度和阻尼性能提升的机床立柱结构优化设计
张轶杰
上海理工大学机械工程学院,上海
收稿日期:2023年3月15日;录用日期:2023年5月12日;发布日期:2023年5月22日

摘要
以三轴直驱立式铣床的立柱为研究对象,以最大化静刚度与固有频率为目标,采用自适应成长法,对机床立柱的加强筋布局进行优化。为同步提升机床的抗振能力,选取对加工精度最敏感的若干个模态作为目标模态,在立柱上布置多级谐质量阻尼器(TMD)系统并确定了其最优安装位置及调谐参数。机床的动静态仿真结果表明,通过该设计方法,在立柱减重8.7%的同时维持了机床原有的动静态刚度性能,并在目标模态处对结构的振动响应进行了有效的抑制,验证了加强筋-TMD组合结构的设计可行性。
关键词
自适应成长法,立柱结构,加强筋布局优化,多目标优化,调谐质量阻尼器

Optimization Design of Machine Tool Column Structure Based on Dynamic and Static Stiffness and Damping Performance Improvement
Yijie Zhang
School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai
Received: Mar. 15th, 2023; accepted: May 12th, 2023; published: May 22nd, 2023

ABSTRACT
The column of a three-axis direct drive vertical milling machine was as research object. Adaptive growth method was adopted to optimize the layout of stiffeners of machine tool column, aiming at maximizing the static stiffness and natural frequency. In order to improve the anti-vibration ability of the machine tool synchronously, several modes which were most sensitive to the machining accuracy were selected as the target modes, a multiple TMD system was arranged on the column and its optimal installation position and tuning parameters were determined. The dynamic and static simulation results of the machine tool show that the column structure maintains the original dynamic and static stiffness performance while the weight is reduced by 8.7%. Moreover, the vibration response of the structure is effectively suppressed at the target mode, which verifies the design feasibility of the stiffener-TMD composite structure.
Keywords:Adaptive Growth Method, Column Structure, Stiffener Layout Optimization, Multiple Objectives Optimization, Tuned Mass Damper

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
立柱作为立式铣床机床的中间支撑件,下接床身,上接滑座、主轴箱等运动部件,起到提供支撑和传递载荷的作用,因此立柱的动静态力学性能对机床的加工精度和切削效率有着至关重要的作用。立柱因承受运动件重力载荷或加工时的反作用力而产生的结构变形会经过前端部件的逐级放大,进而影响刀尖点的运动轨迹,而其动态刚性和动态稳定性也会直接影响整机的固有频率和加工时的振动响应幅值。因此,为提升机床的综合力学性能,有必要在设计时确保立柱具有较好的动静态刚度以及阻尼性能。
由于机床立柱主要承受弯曲和扭转载荷作用,通常采用加筋箱型结构。然而在传统的机床部件设计中,其筋板布局往往基于经验设计,通过增加重复的周期数量以及筋板厚度来达到提升部件刚度的效果,难以达到轻质高刚的设计目的。为获得最优的加强筋布局,学者们提出了一系列不同的拓扑优化方法,如变密度法 [1] 、水平集法 [2] 、变厚度法 [3] 、均匀化方法 [4] 等。Jiao [5] 等人以机床床身的刚度和固有频率为约束,通过拓扑优化大大减轻了床身结构的重量。Park和Youn [6] 提出了一种自适应内正面水平集方法来设计加强肋布局。Du和Olhoff [7] 针对自由振动结构的单阶及多阶固有频率优化问题,讨论了不同的SIMP (Solid Isotropic Material with Penalization)法优化模型对求解该问题的有效性。然而上述优化方法都只能获得隐式的优化结果,设计人员在后处理阶段无法准确地提取结构特征,使所得结果失去最优性。
针对这类有特定结构特征需求的设计问题,Dorn等 [8] 最先提出了用杆单元建立基结构并将连续体拓扑优化问题转换为杆单元尺寸优化问题的基结构法,该方法可以获得显式的优化结果,有利于解决实际的设计问题。丁晓红 [9] [10] [11] 等从自然界植物根系的生长机理中获得启发,提出一种基于灵敏度计算的自适应成长法(Adaptive Growth Method, AGM),通过构建由板壳单元组成的基结构,自适应成长法可以获得清晰的加强筋布局。李宝童等 [12] [13] [14] 也根据类似的仿生思想提出了针对加强筋布局优化的叶脉成长法,并以此为基础提出了增强刚度转移法(Enhanced Stiffness Transformation Approach, ESTA),使加强筋摆脱了基结构对其生长方向和长度的限制,但也因筋板的生长自由度过大,容易出现不连续筋板、平行筋板等问题,而由此衍生出的后处理过程则再次减弱了筋板布局的最优性。
结构的动态性能除与结构的刚度有关外,还与结构的阻尼性能有关。调谐质量阻尼器(TMD)因其阻尼性能好、体积小、设计及安装成本低等特点,在土木、建筑、机械等领域的振动抑制问题中起到了较好的作用。Fei等人 [15] 对切削加工过程中的工件布置TMD,有效抑制了铣削加工过程中的颤振问题,提高了加工系统的切削稳定性和加工精度,并提升了机床的使用寿命。宋吉祥等人 [16] 研究了在周期载荷与冲击载荷下,不同数量和分布形式的TMD对系统的振动抑制效果。Brecher等人 [17] 提出了一种多级多质量阻尼器(MMD)的解析调节方法,弥补了单个TMD振动抑制带宽窄的问题并提升了TMD在失谐系统中的鲁棒性。沈磊等人 [18] 考虑了TMD与结构加强筋布局之间相互作用关系,提出了一种TMD与加强筋布局的协同优化方法,获得了更优于传统顺序优化方法的振动抑制效果。但上述这些研究大多只考虑结构动静态刚度或抗振阻尼性能中的一种,缺少对二者的综合考虑。
本文以立式铣床的立柱结构设计为例,将加强筋布局与TMD的参数调谐同时结合到立柱的结构设计问题中,利用加强筋轻质高刚的结构特征提升立柱的动静态刚度,而对于工作频段中无法避免的共振情况,则用多级TMD系统提升机床的阻尼性能,对多个关键频段的振动响应进行抑制。机床关键位置的局部变形、整机固有频率以及振动位移响应曲线将被用于评价机床综合力学性能,验证加强筋-TMD结构的设计有效性。
2. 设计对象及其动静态性能分析
2.1. 设计对象
图1(a)为某三轴直驱立式铣床,由作为支撑件的床身、立柱和作为运动件的滑座、滑枕、工作台组成。其中,立柱的变形不仅会直接引起前端运动件的位移进而影响刀具的位置,还会增加安装在立柱上的导轨的直线度误差,这一误差将随着运动件的位置变化而改变,大大降低了导轨的导向精度和刀具移动时的精度维持性能。因此选取立柱部件为研究对象,建立机床的有限元模型如图1(b)所示。
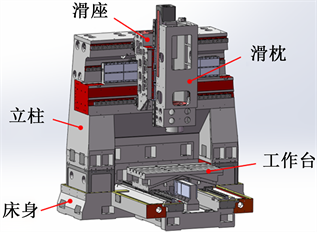 (a) 机床几何模型
(a) 机床几何模型
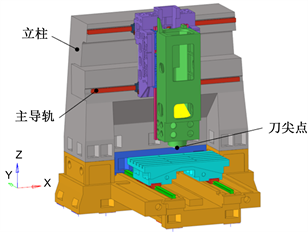 (b) 机床有限元模型
(b) 机床有限元模型
Figure 1. Model of three-axis direct drive vertical milling machine
图1. 三轴直驱立式铣床模型
2.2. 静刚度分析
立式铣床在加工过程中受到的主要外界载荷为加工平面内的切削力,而立柱由切削力所产生的变形可视为X方向切削力导致的整机扭转变形和Y方向切削力导致的整机弯曲变形的组合,本文以高速钢铣刀端铣铝合金工件作为研究工况,切削力大小可由经验公式计算获得:
(1)
其中刀具材料修正系数CP为297;铣削深度ap为1.8 mm;每齿进给量fz为0.5 mm;铣削宽度B为8 mm;铣刀齿数Z为4;铣刀直径d为10 mm;工件材料修正系数KP为0.75。计算得到切削力为554 N,根据经验比例公式得主切削力Pv = 543 N (X方向),进给力PH = 166 N (Y方向),背向力P0 = 305 N (Z方向)。
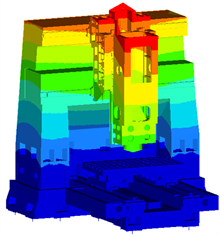
对原结构整机进行有限元分析,机床在切削力作用下的整机静力学仿真结果如图2所示,以刀尖点的位移与立柱主导轨两个法向方向(Y和Z向)上的变形作为衡量整机静刚度的标准。
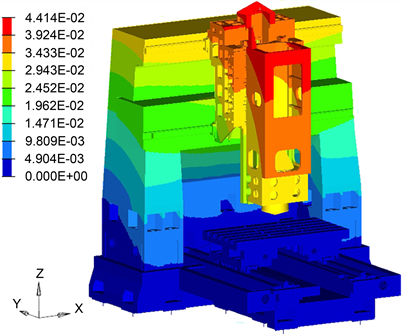
Figure 2. Statics analysis results of machine tools
图2. 机床静力学分析结果
 (a) 主导轨Y方向变形曲线
(a) 主导轨Y方向变形曲线
 (b) 主导轨Z方向变形曲线
(b) 主导轨Z方向变形曲线
Figure 3. Column main rail deformation under cutting force
图3. 切削力作用下的立柱主导轨变形
从图2、图3的仿真结果可知,立柱、滑座与滑枕的变形使刀尖点产生了28.29 μm的位移,同时立柱主导轨在法向方向上也出现了一定程度的变形。因此,提升立柱结构的抗弯与抗扭刚度有利于提升机床的加工精度与加工稳定性。
2.3. 动力学性能分析
研究机床的动力学性能可以帮助了解结构自身的固有动态属性,并预测在外界载荷激励下机床的振动响应,从而找到当前结构的薄弱点,制定相应的优化方案。
对机床进行模态分析可以得到其自振频率以及相应的模态振型,而结构的低阶模态往往更容易被激发,因此对整机的前六阶模态进行分析。整机的前六阶模态频率与振型如下图4所示。
 (a) 第一阶模态(50.2 Hz)
(a) 第一阶模态(50.2 Hz)
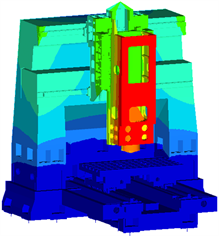 (b) 第二阶模态(83 Hz)
(b) 第二阶模态(83 Hz)
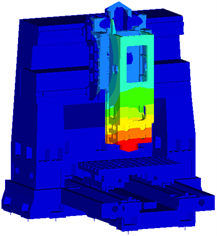 (c) 第三阶模态(111.4 Hz)
(c) 第三阶模态(111.4 Hz)
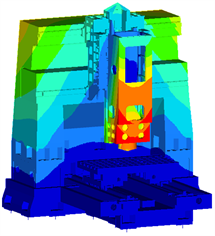 (d) 第四阶模态(129.6 Hz)
(d) 第四阶模态(129.6 Hz)
 (e) 第五阶模态(159.4 Hz)
(e) 第五阶模态(159.4 Hz)
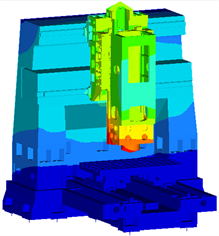 (f) 第六阶模态(176.5 Hz)
(f) 第六阶模态(176.5 Hz)
Figure 4. The first six modes of machine tool
图4. 机床前六阶模态
可以看到,整机的前六阶模态中有五阶的振型与立柱的振动有关,分别是以立柱前后弯曲为主要振型的第一和第六阶模态以及以立柱扭转为主要振型的第二、四和五阶模态,因此优化立柱的动刚度对提升机床的低阶模态频率有重要意义。
由于机床加工时受到的激振频域较宽,不可避免的会覆盖到机床的低阶模态,因此有必要结合前六阶模态分析的结果,对机床进行谐响应分析,将切削力以谐响应载荷的形式加载至刀尖点位置,刀尖点在三个方向上的位移频响曲线如图5所示。在X方向的频响曲线中存在三个位移峰值点,分别对应整机的第二、四、五阶模态,即机床的扭转振型,其中第二阶模态频率处的响应峰值最高;Y方向的频响曲线中存在两个峰值点,其中第一个峰值点发生在第一阶模态频率处并对应机床的前后弯曲振型,第二个峰值点出现在第三阶模态频率处,对应的模态振型为滑枕的局部弯曲变形,且该处的响应峰值远高于前者;Z方向存在两个主要的响应峰值点,与Y方向的情况类似,同样对应第一阶模态与第三阶模态,其中第一阶模态频率处的最大位移响应在Y与Z方向数值相近,而第三阶模态频率处Z方向的最大位移响应则明显小于Y方向。由此可知,强化立柱的抗振性能有助于提升机床在X和Z方向的加工精度。
 (a) X方向频率–位移响应曲线
(a) X方向频率–位移响应曲线
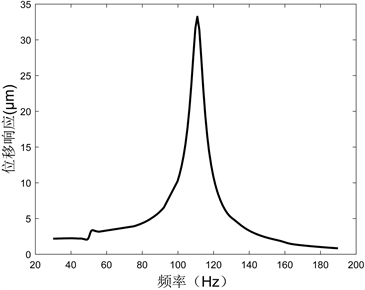 (b) Y方向频率–位移响应曲线
(b) Y方向频率–位移响应曲线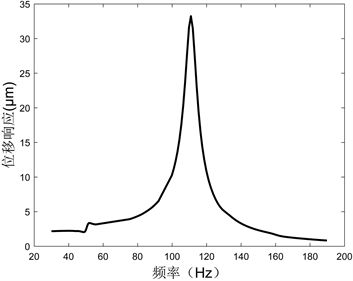 (c) Z方向频率–位移响应曲线
(c) Z方向频率–位移响应曲线
Figure 5. Frequency response curve of cutter tip under harmonic load
图5. 简谐载荷下的刀尖点频响曲线
3. 基于自适应生长的筋板布局优化方法
3.1. 自适应成长法则
自然界中,植物为了适应不同的生长环境会演化出形态、功能各异的根系和茎秆结构,这些结构使得不同植物能根据自身特有的生物特性找到最高效的养分汲取途径和自支撑形态,而其生长过程则可看作是每株植物个体针对当前外界环境所给出的约束条件为自身寻找最优解的过程。不论是养分的运输还是提供自支撑刚性,都能抽象为给不同形式的能量规划最佳的传递路径,而这一概念恰好与工程问题中的加强筋布局设计高度相似。通过引入自适应成长法则,加强筋的布局也可以根据不同的支撑、载荷条件,针对不同的力学性能需求设计出最佳的能量传递路径,从而实现结构的最优设计。
以三维箱型结构为例,首先在模型内根据载荷约束条件选择“种子点”作为筋板生长的初始起点,筋板(壳单元)从“种子点”开始向全局方向生长,并在到达一定厚度值后拥有“分支”能力,将其周围的筋板单元填加到设计变量中参与后续的优化迭代。整个迭代过程基于筋板厚度对目标函数的灵敏度分析,有利于实现优化目标的筋板将快速分支、生长,反之则会被退化。通过不断重复这一过程,最终获得符合性能需求的最优筋板布局。
3.2. 模型建立
为构建可供筋板“生长”的三维箱体模型,首先用线性六面体单元对箱体进行离散化,并基于箱体外侧表面的节点建立带有厚度尺寸的壳单元,用于模拟箱体的外壳。随后在每个六面体单元内根据设计规定的拔模方向建立壳单元,用于模拟筋板结构。外壳作为优化问题的非设计域,模型内的其他壳单元则为加强筋结构的可设计域。其中,外壳的厚度为指定设计对象的实际厚度,筋板单元的初始厚度为某较小值。
值得关注的是,尽管在静力学问题中小厚度的筋板对结构整体力学性能的影响有限,但在动力学问题中基结构却会对结构的动刚度产生不可忽视的影响 [19] 。为此引入基于筋板厚度的材料惩罚机制,如式(2)所示,使处于生长初期或不重要的小厚度筋板更轻、更软,而对生长“成熟”的大厚度筋板赋予材料的真实属性。
(2)
其中,Eh和ρh为第h个筋板在优化过程中的弹性模量和密度;E和ρ为其材料原有的弹性模量和密度;Tmin、Tm、Tmax分别对应筋板的最小厚度、成熟厚度及最大厚度;P为惩罚因子,本文中取值为5。通过公式(2)的材料惩罚,有效降低了基结构对动力学性能和局部模态等问题的影响。
3.3. 设计流程
基于自适应成长法的筋板布局优化的流程可分为以下四步:
1) 建立箱体基结构模型
根据目标模型尺寸建立三维箱体结构并将其用六面体单元离散网格化,参考2.2中的方法建立箱体的外壳以及内部的周期性基结构,其中箱体外壳设为非设计域。
2) 设置优化参数并选择种子点
根据设计对象设置筋板厚度的最大值Tmax、初始值Tinit以及其成熟厚度Tm,当筋板由初始厚度增长至Tm及以上时赋予其“分支”能力,可将其周围的加强筋单元激活并参与优化迭代。此外,厚度低于Tm的加强筋的材料属性会根据式(2)进行惩罚,以消除基结构对箱体动力学性能的影响。基结构中的壳单元为优化的设计域,为降低其计算量,设计域中的单元只有在被激活为“活动筋板”时才会加入优化迭代的计算,而最初的“活动筋板”则通过“种子点”的选择来确定。
3) 灵敏度分析
对建立的箱型结构进行有限元分析,计算其动静态力学性能,并如式(3)计算“活动筋板”的厚度关于目标函数的灵敏度,加强筋会根据下降梯度最速的方向进行生长。为保证箱体内的加强筋结构满足拔模约束,对投影方向的筋板灵敏度求平均。
(3)
4) 加强筋更新并重构模型
根据灵敏度计算的结果,用MMA算法对所有“活动筋板”的厚度进行更新,同时根据式(2)的材料插值方法赋予其新的材料属性。当更新后的“活动筋板”厚度大于Tm时,与其相连的筋板则会被激活为“活动筋板”参与下一步的优化迭代,等于Tinit则被“退化”,从“活动筋板”中移除。
重复(3)、(4)步骤的迭代过程,直到满足以下两个收敛条件时优化结束:1) 连续三次迭代的目标函数值变化小于容差ε;2) 优化迭代次数大于设定最大值。
4. 立柱筋板布局优化设计
4.1. 设计模型
为用上述加筋优化方法对立柱的动静态力学性能进行优化,将立柱主要的加筋区域简化为规则的矩形箱体,拔模方向设置为Y方向,如图6所示。
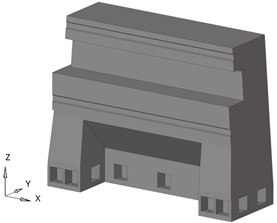 (a) 几何模型
(a) 几何模型
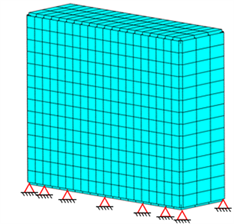 (b) 设计模型
(b) 设计模型
Figure 6. Simplification of column model
图6. 立柱模型简化
箱体的约束条件根据立柱与床身的螺栓连接位置对14个节点进行全自由度约束,载荷则如式(7)通过力的平移定理将1.1节中的切削力以及主轴箱和滑座的重力等效为立柱上的集中力和力矩,由导轨滑块副的四个滑块进行传递,如图7所示。箱体结构的优化同样需要考虑主轴处于不同位置时立柱的整体刚度,因此设置了主轴处于左极限位、中间位以及右极限位的三种工况。
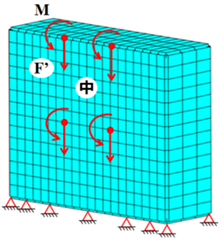 (a) 载荷等效
(a) 载荷等效
 (b) 工况设置
(b) 工况设置
Figure 7. Working conditions setting of column
图7. 立柱工况设置
(4)
其中,F为原载荷,F'为平移至每个滑块作用点上的等效力,M为等效力矩,e为原载荷作用点到滑块的偏心距。
在立柱的动力学优化问题的建模中,为了更符合立柱在装配状态下的模态特征,将滑枕与滑座简化为四个质量点加载于四个滑块所在的位置,并同样考虑滑枕工作位置的不同对整体模态的影响,根据滑枕位置建立左极限位、中间位以及右极限位三个模态工况。
4.2. 优化模型及过程
为合理分配不同结构的功能与优势特点,从而最大程度地提升结构的综合力学性能,选择用轻质高刚的加强筋结构来提升立柱的静刚度和固有频率,优化数学模型如下所示:
(5)
优化目标为最小化立柱在静态工况下的全局应变能并最大化立柱前六阶固有频率,通过带权重的折中规划得到目标函数。其中,w为动静态问题的权重系数;i对应不同加工位置时的三种工况;Ci(T)为静载荷下的全局应变能; 、 分别为优化前第i工况下的全局应变能以及针对其单工况优化后的全局应变能; 为立柱的第i阶固有频率; 、 分别为i工况优化前的第j阶固有频率以及对其单目标优化后的第j阶固有频率; 为不同工况之间的加权系数; 为i工况下前六阶固有频率之间的加权系数;η是由优化前后的体积v0与v之比所得的体积分数。
为了使筋板的“生长”趋势更符合力的传递路径,同时也能给予算法更合适的初值,将图7中的8个载荷作用点以及14个约束点作为“种子点”,加强筋将以“种子点”为起点向灵敏度最大的方向生长,使载荷与支撑形成闭环连接。图8(a)为优化迭代的第一步,“种子点”附近的基结构单元被激活为“活动筋板”,随着迭代步的增加,更多的筋板被激活并参与迭代,大量的低厚度筋板逐步被少数更厚的筋板所取代,最终经过图8(b)、图8(c)所示的迭代过程生长为图8(d)中的筋板布局。图8(e)为立柱的全局动柔度与筋板体积的迭代变化曲线。
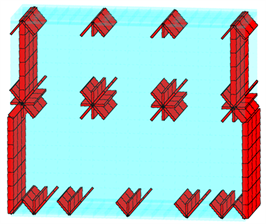 (a) 第2步迭代
(a) 第2步迭代
 (b) 第7步迭代
(b) 第7步迭代
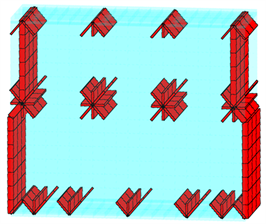 (c) 第15步迭代
(c) 第15步迭代
 (d) 第74步迭代
(d) 第74步迭代
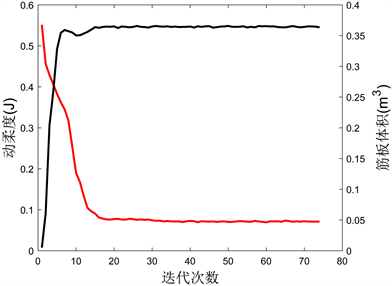 (e) 迭代曲线
(e) 迭代曲线
Figure 8. Iterative process of stiffener layout optimization
图8. 筋板布局优化迭代过程
立柱的加筋优化在74个迭代步后完成收敛,其大致的拓扑结构在优化前15步内便已逐渐成型,而后续的迭代过程则可视为对筋板厚度的尺寸优化,细小的分支筋板退化消失,多余的材料则进一步增加主体筋板的厚度,最终形成封闭且连续的加强筋结构。与初始的“米”字型筋板布局相比,优化后的结构明显增加了交叉斜筋相对于竖筋的比重,且斜筋的分布方式也与原结构有较大差异,这使得目前的立柱结构能更好地适应其实际加工工况,有效地应对可能影响机床加工精度的结构变形及振动。
4.3. 结果对比
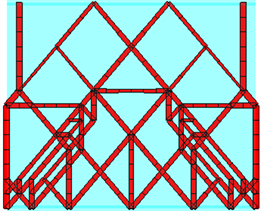
基于图8(d)的设计结果,进行工程化设计,最终的立柱筋板布局如图9所示。优化后的立柱相较于原结构减重8.7%,使用HT300为铸造材料时可减重416 KG。
将其装配至整机模型中再次进行有限元分析,与1.1、1.2节中的分析结果进行对比。表1为优化前后刀尖点的静态位移对比,可以看到优化后的立柱结构在减轻重量的同时也降低了静力载荷下刀尖点在各个方向上的位移,使机床整体静刚度得到了小幅度的提升。图10为优化前后主导轨的直线度误差对比,由于导轨上的节点位移包含了导轨自身的变形以及立柱的变形,且后者在优化前后的大小不同,故无法直接从图中读取直线度误差。为了更直观地进行对比,连接导轨两端作直线,并过直线两侧最大变形点作平行包络线,计算两包络线之间的距离,结果如表2所示。可以看到优化前后的直线度误差变化均在0.06 μm以内,优化后的结构在Y方向上拥有更小的直线度误差,而在Z方向上则较原结构略有增加,基本保持立柱原有的静态刚度。
 (a) 优化后的立柱筋板布
(a) 优化后的立柱筋板布
 (b) 工程化后的立柱筋板布局
(b) 工程化后的立柱筋板布局
Figure 9. Stiffener layout of column
图9. 立柱筋板布局
Table 1. Cutter tip displacement under cutting force
表1. 切削力作用下刀尖点位移
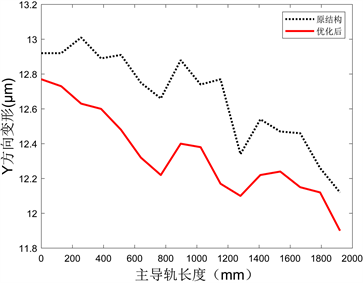 (a) 主导轨Y方向变形曲线
(a) 主导轨Y方向变形曲线
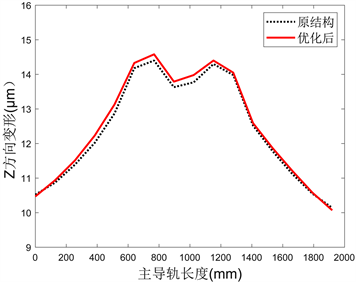 (b) 主导轨Z方向变形曲线
(b) 主导轨Z方向变形曲线
Figure 10. Deformation curve of column main rail
图10. 立柱主导轨的变形曲线
Table 2. Comparison of straightness error in the normal direction of the main rail
表2. 主导轨法向方向直线度误差对比
优化后的前六阶模态振型不变,其固有频率的前后变化幅度如图11所示,前五阶模态频率较优化前均有不同程度的上升,第六阶仅下降0.1 Hz,其中提升幅度最大的第二、四、五阶模态均与立柱的扭转有关,而第一、六阶模态则与立柱的弯曲有关,该趋势与静刚度的变化情况一致。从上述分析结果中可以看到,在减重8.7%的情况下,整机的动静态力学性能基本维持原有水平甚至获得了小幅度的提升,从而证明了立柱筋板布局优化对轻量化以及改善整机综合力学性能的有效性。
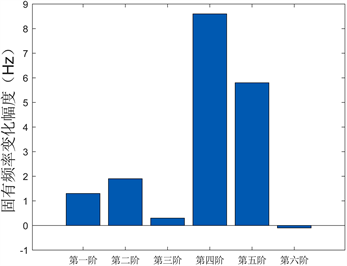
Figure 11. The natural frequency change of the machine tool after optimization
图11. 优化后的整机固有频率变化
5. 阻尼器调谐优化
提升结构的动态性能需要同时考虑其动刚度及阻尼性能,前文通过对加强筋布局进行优化,使机床在减重的同时也提高了自身的固有频率,而对于实际加工中无法避开的低阶共振频率,可通过在结构外部安装调谐质量阻尼器来为机床提供额外的阻尼性能,从而实现对结构振动的有效抑制。
5.1. 箱型结构–阻尼器有限元建模
若将箱型结构的连续体有限元模型视为单自由度系统,如图12(a),用质量M0,刚度K0,阻尼C0来表示,且假设箱型结构安装有n个TMD,每个阻尼器用质量mj,刚度kj,阻尼cj (j = 1, ∙∙∙, n)来表示,则该主结构–阻尼器系统在受到外部简谐载荷Feiωt时满足振动平衡方程:
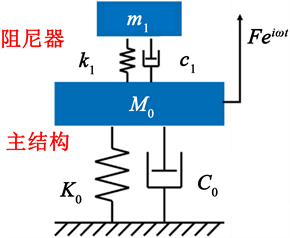 (a) 单自由度箱体模型
(a) 单自由度箱体模型
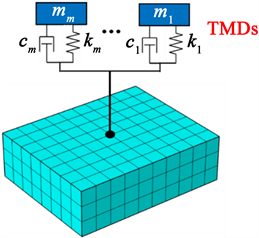 (b) 多自由度箱体模型
(b) 多自由度箱体模型
Figure 12. The diagram of box-TMD model
图12. 箱体-TMD模型示意图
(6)
其中,u0和uj分别为主结构和第j个TMD的位移,ω为激振频率。
在有限元模型中,单个阻尼器的安装对应箱体表面上的单个节点,将箱体视为连续体结构如图12(b),主结构–阻尼系统的整体刚度矩阵K与质量矩阵M均由主结构与阻尼器各自的矩阵组装得到,而主结构的阻尼相对TMD而言可忽略不计,因此阻尼器的阻尼矩阵即可视为整体的阻尼矩阵。系统的属性矩阵表示如下:
(7)
上式中的 与 为主结构的刚度与阻尼矩阵,其构成为标准的连续体有限元模型矩阵形式; 与 分别为阻尼器的刚度与阻尼矩阵,对于结构中存在n个阻尼器的情况,单个阻尼器的属性矩阵为简单的对称矩阵,如式(8)所示
(8)
5.2. 阻尼器参数优化
TMD的作用原理是附加与主结构共振频率相近的质量–刚度–阻尼系统,利用质量块与主结构的振动相位差削弱振动幅度,并通过阻尼将振动能量转化为热能进行耗散。TMD的设计不仅需要对其刚度、阻尼进行调谐,从而使阻尼器与主结构的共振频率尽可能地接近,还需要考虑其质量块的大小、安装位置以及阻尼器的数量,才能最大程度地发挥其减振效果。
在对TMD的刚度和阻尼参数进行优化之前,首先需要确定TMD的质量、数量及安装位置。以往的设计中通常将主结构抽象为单自由度,根据理论公式计算TMD刚度、阻尼参数的调谐值,而忽略了安装位置对其减振性能的影响 [17] 。对于不同的TMD位置,可以通过式(9)计算安装阻尼器后结构第r阶模态下的等效模态质量Mr:
(9)
其中 和 分别为主结构附加额外质量前后的第r阶频率。计算结果显示,当阻尼器安装在第r阶模态的最大模态位移处时,主结构的Mr最小,这意味着相同附加重量下此时阻尼器与主结构的质量比最大,起到的减振作用也最佳。从上述分析中可以看到,所谓的最佳安装位置只是针对某一个目标模态而言的,由于单一的TMD仅对某一阶振型有控制作用 [20] ,因此对于不同的目标模态也要确定相应的安装位置。
TMD的质量越大,对主结构产生的惯性力越大,同时其阻尼带宽也随之会增大 [21] ,但额外的附加质量也可能会带来部分结构模态频率降低的问题,因此在实际工程问题中TMD与主结构的质量比一般控制在0.005~0.03之间,本文中的立柱结构重量大约为6吨,故针对每个目标模态的附加质量选择为30 KG。
理想情况下可以将工作频段内的每阶模态都作为目标模态,设计对应的TMD,但这也会导致总的附加质量过重以及TMD之间安装位置出现干涉的情况。此外,随着结构中附加的TMD数量增加,虽然整体的位移抑制效果也会呈非线性的缓慢增加,但平均到每个TMD上的效率则明显下降 [21] ,因此在确定目标模态时应结合实际问题选择优先级最高的模态进行抑制。从图5的原结构谐响应分析中可以看到,对机床三个方向的加工精度影响最显著且与立柱相关的模态为第一阶(50.2 Hz)与第二阶(83 Hz)模态,因此将其选为振动抑制的目标模态,每个目标模态配置两个TMD,因此单个TMD的质量为15 KG。根据式(9)的计算,两组TMD的安装位置如图13所示。
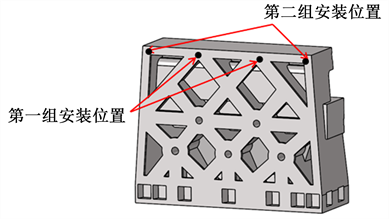
Figure 13. Installation position of TMDs
图13. TMD安装位置示意图
在确定了阻尼器的安装位置之后,需要对TMD的刚度、阻尼参数进行调谐优化,以往的设计中会通过理论计算方法获得最优刚度、阻尼参数的近似解析解,当针对H∞优化准则(最小化振动幅值最大值)进行调谐时的近似求解公式如式(10)所示,
(10)
其中 为对第r阶目标模态的固有频率; 为第r阶目标模态的TMD质量;τ为TMD与主结构的质量比。但对于多自由度高度非线性的复杂模型,很难通过该公式获得满足实际需求的最优调谐参数,因此需要在整机有限元模型中利用数值优化算法求得刚度、阻尼参数的数值最优解。使用序列二次规划算法(SQP)进行优化计算,参数优化的数学模型如下:
(11)
式中, 为主结构在目标模态下的最大动柔度,将式(10)计算所得近似解析解作为kr与cr的初始值,以避免出现局部最优解并且可以更快地完成收敛。最终调谐优化所得的第一组TMD刚度为3980 N/mm,阻尼为0.85 N*S/mm;第二组TMD刚度为9100 N/mm,阻尼为1.41 N*S/mm。
图14为安装TMD前后的刀尖点位移响应对比,可以看到在通过TMD对第一阶与第二阶模态进行振动抑制后,50 Hz和83 Hz处的位移响应峰值发生了明显的变化。第一阶模态所对应的立柱弯曲变形主要影响刀具Z方向的振动位移响应,在安装TMD后其响应峰值从4.5 μm降低至3.5 μm,Y方向的位移响应也受其影响,在50 Hz处从3.4 μm降低至2.9 μm,而受第二阶模态对应的立柱扭转变形影响最大的X方向位移响应峰值则从23.6 μm降低至14.6 μm,而其他频率的位移响应峰值则没有发生明显的变化,所选用的TMD在显著降低了目标模态位移响应峰值的同时也并没有使该阶模态的频率发生前移。由此可见,通过在机床立柱上安装TMD对特定频率下的振动响应进行抑制的方法有效且可行,附加阻尼器对机床阻尼性能的强化可显著减小刀具在振动激励下的位移响应幅值,从而降低零件加工的表面粗糙度。
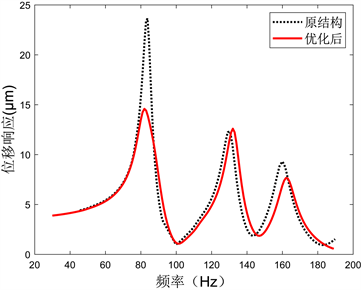 (a) X方向对比
(a) X方向对比
 (b) Y方向对比
(b) Y方向对比
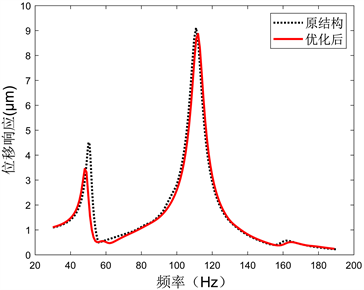 (c) Z方向对比
(c) Z方向对比
Figure 14. Comparison of cutter tip displacement response before and after optimization
图14. 优化前后的刀尖点位移响应对比
6. 结论
本文通过对机床的动、静态进行有限元分析,探讨了立柱结构对机床加工性能的影响;将加筋结构与多级TMD系统的组合形式应用于立柱结构的设计中,根据其各自的功能优势分配相应的设计目标并进行优化,使立柱乃至整机的动静态刚度以及阻尼性同时获得提升。首先以立柱的静柔度及固有频率为目标,采用自适应成长法对其加强筋布局进行优化,在减重8.7%的基础上使立柱保持了原有的静刚度水平并在固有频率上获得了一定程度的上升;之后选取了两阶对加工精度影响最为敏感的模态作为目标模态,通过优化得到了两组TMD的最佳安装位置以及调谐参数,使整机在两阶目标模态下的刀尖点位移响应大幅下降。本文提供的设计案例证明了加强筋–多级TMD系统对提升结构动静态刚度及减振性能的有效性,且本文所提出的设计方法具有可应用性强、设计周期短的优势,对实际的工程设计问题具备一定的参考价值。
致谢
十分感谢导师丁晓红教授在本人完成课题期间在相关专业理论知识和研究思路上的悉心指导以及平台资源的提供,丁老师在严格把关研究过程与成果的同时,也给予了学生充分的思考和创新空间,鼓励学生主动探索问题并尝试不同的解决途径,其对待科研问题的认真与专注以及分析问题时灵活且严谨的思维,给我的科研不断带来激励与启发。同样也感谢课题组的张横、王瀚、熊敏老师和沈磊师兄在课题中给我提供的建议与技术支持,帮助我从更多角度认识问题、解决问题。最后希望在课题组的继续努力下,未来能在机床结构优化设计的领域中取得更好的研究成果。
基金项目
国家重点研发计划(2022YFB4600184);国家自然科学基金资助项目(52005337)。
文章引用
张轶杰. 基于动静态刚度和阻尼性能提升的机床立柱结构优化设计
Optimization Design of Machine Tool Column Structure Based on Dynamic and Static Stiffness and Damping Performance Improvement[J]. 建模与仿真, 2023, 12(03): 2359-2375. https://doi.org/10.12677/MOS.2023.123217
参考文献
- 1. Sigmund, O. (2001) A 99 Line Topology Optimization Code Written in Matlab. Structural and Multidisciplinary Optimization, 21, 120-127. https://doi.org/10.1007/s001580050176
- 2. Mei, Y. and Wang, X. (2004) A Level Set Method for Struc-tural Topology Optimization and Its Applications. Advances in Engineering Software, 35, 415-441. https://doi.org/10.1016/j.advengsoft.2004.06.004
- 3. Lam, Y. and Santhikumar, S. (2003) Automated Rib Location and Optimization for Plate Structures. Structural and Multidisciplinary Optimization, 25, 35-45. https://doi.org/10.1007/s00158-002-0270-7
- 4. Ansola, R., Canales, J., Tarrago, J.A. and Rasmussen, J. (2004) Com-bined Shape and Reinforcement Layout Optimization of Shell Structures. Structural and Multidisciplinary Optimization, 27, 219-227. https://doi.org/10.1007/s00158-004-0399-7
- 5. Jiao, M., Guo, X.H. and Wan, D.D. (2012) Finite Element Analysis and Lightweight Research on the Bed of a Large Machine Tool Based on HyperWorks. Applied Mechanics and Materials, 121-126, 3294-3298. https://doi.org/10.4028/www.scientific.net/AMM.121-126.3294
- 6. Park, K.-S. and Youn, S.-K. (2008) Topology Op-timization of Shell Structures Using Adaptive Inner-Front (AIF) Level Set Method. Structural and Multidisciplinary Optimiza-tion, 36, 43-58. https://doi.org/10.1007/s00158-007-0169-4
- 7. Du, J.B. and Olhoff, N. (2007) Topological Design of Freely Vibrating Continuum Structures for Maximum Values of Simple and Multiple Eigenfrequencies and Frequency Gaps. Structural and Multidisciplinary Optimization, 34, 91-110. https://doi.org/10.1007/s00158-007-0101-y
- 8. Dorn, W.C., Gromory, R.E. and Greeberg, H.J. (1964) Automatic Design of Optimal Structures. Journal de Mecanique, 3, 22-52.
- 9. Ding, X.H. and Yamazaki, K. (2005) Adaptive Growth Technique of Stiffener Layout Pattern for Plate and Shell Structures to Achieve Minimum Compliance. Engineering Optimization, 37, 259-276. https://doi.org/10.1080/0305215512331328231
- 10. 丁晓红, 李国杰. 箱型支撑结构加筋板布局设计方法研究[J]. 中国机械工程, 2012, 23(4): 449-453. https://doi.org/10.3969/j.issn.1004-132X.2012.04.019
- 11. Zhang, H., Ding, X.H., Dong, X.H. and Xiong, M. (2018) Optimal Topology Design of Internal Stiffeners for Machine Pedestal Structures Using Biological Branching Phenomena. Structural and Multidisciplinary Optimization, 57, 2323-2338. https://doi.org/10.1007/s00158-017-1862-6
- 12. Li, B.T., Hong, J., Yan, S. and Liu, Z.F. (2013) Multidiscipline Topology Optimization of Stiffened Plate/Shell Structures Inspired by Growth Mechanisms of Leaf Veins in Nature. Mathematical Problems in Engineering, 2013, Article ID: 653895. https://doi.org/10.1155/2013/653895
- 13. Li, B.T., Ge, L.H. and Hong, J. (2017) An Intelligent Computational Approach for Design Optimization of Stiffened Engineering Structures. International Journal of Precision Engineering and Manufactur-ing, 18, 1005-1012. https://doi.org/10.1007/s12541-017-0118-0
- 14. Li, B.T., Xuan, C.B., Tang, W.H., et al. (2019) Topology Optimization of Plate/Shell Structures with Respect to Eigenfrequencies Using a Biologically Inspired Algorithm. Engineering Optimization, 51, 1829-1844. https://doi.org/10.1080/0305215X.2018.1552952
- 15. Fei, J.X., Lin, B., Yan, S., et al. (2017) Chatter Mitigation Using Moving Damper. Journal of Sound and Vibration, 410, 49-63. https://doi.org/10.1016/j.jsv.2017.08.033
- 16. 宋吉祥, 吴炜, 严定帮, 等. 冲击/周期载荷作用下分布式调谐质量阻尼器对响应控制的影响[J]. 上海航天(中英文), 2021, 38(1): 13-19. https://doi.org/10.19328/j.cnki.1006-1630.2021.01.002
- 17. Brecher, C., Schmidt, S. and Fey, M. (2016) Analytic Tuning of Robust Multi-Mass Dampers. CIRP Annals, 65, 365-368. https://doi.org/10.1016/j.cirp.2016.04.102
- 18. Shen, L., Ding, X.H., Hu, T.N., Zhang, H. and Xu, S.P. (2021) Simultaneous Optimization of Stiffener Layout of 3D Box Structure Together with Attached Tuned Mass Dampers under Harmonic Excitations. Structural and Multidisciplinary Optimization, 64, 721-737. https://doi.org/10.1007/s00158-021-02880-9
- 19. Hu, T.N., Ding, X.H., Shen, L. and Zhang, H. (2020) Im-proved Adaptive Growth Method of Stiffeners for Three-Dimensional Box Structures with Respect to Natural Frequencies. Computers & Structures, 239, Article ID: 106330. https://doi.org/10.1016/j.compstruc.2020.106330
- 20. 王鹏, 杨明亮, 李哲人, 等. 基于改进遗传算法的TMD阻尼器的优化布置[J]. 机床与液压, 2019, 47(16): 17-21, 29. https://doi.org/10.3969/j.issn.1001-3881.2019.16.004
- 21. 同长虹, 张小栋. 调谐质量阻尼器参数优化及其应用[J]. 振动、测试与诊断, 2007, 27(2): 146-149. https://doi.org/10.3969/j.issn.1004-6801.2007.02.013
