基于潜伏感染和饱和发生率的HIV感染模型 An HIV Infection Model Based on Latent Infection and Saturated Incidence Rate

doi:10.12677/AAM.2022.115308

Advances in Applied Mathematics
Vol. 11 No. 05 ( 2022 ), Article ID: 51827 , 13 pages
10.12677/AAM.2022.115308

基于潜伏感染和饱和发生率的HIV感染模型

宋世杰，陈莺蓉，李朋朔，王艳

●How to Cite this Article

中国石油大学(华东)理学院，山东青岛

收稿日期：2022年4月25日；录用日期：2022年5月19日；发布日期：2022年5月27日

摘要

本文根据HIV在感染者体内的感染过程，考虑到T细胞的潜伏感染以及免疫应答，建立具有饱和发生率的HIV感染模型，来模拟感染过程中病毒颗粒和T细胞之间的相互关系。首先，依据模型求解得到唯一的未感染平衡点 $E_{0}$ 和感染平衡点 $E^{*}$ ，然后通过利用微分方程稳定性理论，得到模型在两类平衡点的局部渐近稳定性，随后在实际参数意义下对模型进行数值模拟，以此验证平衡点的稳定性。最后，通过模型比较，说明所建模型的合理性和正确性。

关键词

HIV病毒，免疫应答，常微分方程，稳定性

An HIV Infection Model Based on Latent Infection and Saturated Incidence Rate

Shijie Song, Yingrong Chen, Pengshuo Li, Yan Wang

College of Science, China University of Petroleum (East China), Qingdao Shandong

Received: Apr. 25^th, 2022; accepted: May 19^th, 2022; published: May 27^th, 2022

ABSTRACT

In this paper, an HIV infection model with saturation incidence rate is developed based on the infection process of HIV in infected individuals, taking into account the latent infection of T cells and the immune response, to simulate the interrelationship between viral particles and T cells during the infection process. Firstly, the model is solved to obtain unique uninfected and infected equilibria $E_{0}$ and infected equilibria $E^{*}$ , and then the local asymptotic stability of the model at the two types of equilibria is obtained by using the stability theory of ordinary differential equation. The model is then numerically simulated in the sense of actual parameters to verify the stability of the equilibrium point. Finally, through the model comparison, the rationality and accuracy of the built model are explained.

Keywords:HIV Virus, Immune Response, Ordinary Differential Equation, Stability

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

艾滋病是当今世界最严重的疾病之一，它具有强大的传播性且难以消灭。21世纪以来，世界各地有大量的艾滋病感染者出现，给家庭和社会都带来了一定的损失因此，因此，如何有效地预防和治疗艾滋病，是当今社会面临的一项重大难题。

艾滋病(Acquired Immune Deficiency Syndrome, AIDS)是当今一种危害性极大的传染病，是由人类免疫缺陷病毒(Human Immunodeficiency Virus, HIV)感染人体后，导致感染者抵抗力明显丧失的一种难以治愈的疾病。HIV病毒在侵入人体后，人体内的T淋巴细胞将受到大量的破坏，T淋巴细胞的丧失会导致人的抵抗力降低和部分免疫功能的丧失，而人在丧失免疫功能后，将极易感染恶性肿瘤等相关疾病，因此艾滋病患者拥有较高的死亡率。HIV在人体内具有很长的潜伏期，在此期间，病毒并不会伤害到感染者，但感染者体内的免疫功能却会逐渐丧失。一旦发病，在病毒的攻击下人体将受到巨大的伤害。

目前，凭借已有的医疗水平并不能很好地消灭艾滋病，因此现阶段的艾滋病治疗的主要目的在于去最大限度和持久地降低人体内HIV病毒含量、提高艾滋病感染者的生活质量以及尽可能地减少艾滋病感染者的死亡率和阻止艾滋病的进一步扩散。其中，免疫调节及免疫重建治疗 [1] 是当前最常见的艾滋病的治疗方法之一。

人们通过多年来的研究，不断地优化和改进HIV病毒动力学模型，模型由最初的经典三维模型 [2] 不断更新。基于前人研究的基础上，本项目从HIV潜伏机制和免疫应答效应入手，建立先前未被研究过的基于饱和发生率的HIV感染模型，求解模型的未感染平衡点 $E_{0}$ 和感染平衡点 $E^{*}$ ，并在理论上验证这两个平衡点的稳定性。该模型的研究更加贴近真实情况，可以对医疗人员提交出有用的数据，为HIV病毒的发展和防治提供数学依据。

2. 基于饱和感染、免疫应答和潜伏感染的HIV模型

2.1. 模型的建立

研究发现饱和发生率对病毒模型研究更具有实际意义，因此为了更好地进行模型分析与研究，我们所讨论的模型将在HIV病毒饱和感染的基础上进行，即建立基于饱和发生率的HIV感染模型。同时，我们发现在病毒感染健康的T细胞时，CD4⁺ T细胞经过一段时间之后被激活才会成为发病的感染CD4⁺ T细胞 [3]，另外人体内含有的CTL免疫细胞会清除部分已被感染的T细胞 [4]，于是，我们将上述因素进行综合考虑，建立了如下模型：

$\begin{array}{l} \frac{d T}{d t} = λ - d_{1} T - \frac{β T V}{1 + a V}, \\ \frac{d L}{d t} = \frac{η β T V}{1 + a V} - α L - d_{2} L, \\ \frac{d I}{d t} = \frac{(1 - η) β T V}{1 + a V} + α L - d_{3} I - p I C, \\ \frac{d V}{d t} = k I - d_{4} V, \\ \frac{d C}{d t} = q I - d_{5} C, \end{array}$ (2-1)

其中， $T (t)$ 表示在t时刻的CD4⁺ T细胞中未受HIV病毒感染的浓度， $I (t)$ 为在t时刻CD4⁺ T细胞中受感染部分的浓度， $V (t)$ 表示t时刻人体体内的病毒粒子浓度， $L (t)$ 表示在t时刻CD4⁺ T细胞中潜伏感染部分的浓度， $C (t)$ 表示t时刻人体体内CTL细胞的浓度。 $λ$ 表示单位时间内生成的未被感染的CD4⁺ T细胞浓度， $d_{1}$ 表示单位时间内死亡的未受感染的细胞浓度， $d_{2}$ 表示单位时间内死亡的潜伏感染的细胞浓度， $d_{3}$ 表示单位时间内死亡的受感染的细胞浓度， $d_{4}$ 表示单位时间内清除的病毒颗粒浓度， $d_{5}$ 表示单位时间内死亡的CTL细胞浓度。 $α$ 表示单位时间里被激活的潜伏感染的CD4⁺ T细胞浓度， $β$ 表示单位时间里被感染的HIV病毒的浓度， $η$ 表示单位时间里被潜伏感染的CD4⁺ T细胞浓度，p表示单位时间里被CTL细胞清除的已感染细胞的浓度，k表示感染CD4⁺ T细胞死亡时释放的HIV病毒颗粒比率，q表示单位时间里受已感染细胞的影响CTL细胞的浓度。

2.2. 模型平衡点

模型(2-1)存在唯一的未感染平衡点 $E_{0} = (T_{0}, 0, 0, 0, 0)$ ，其中 $T_{0} = \frac{λ}{d_{1}}$ 。

定义模型(2-1)的基本再生常数 $R_{0}$ ：

$R_{0} = \frac{[α + (1 - η) d_{2}] β k λ}{d_{1} d_{3} d_{4} (α + d_{2})} .$

接下来，我们求解模型(2-1)的感染平衡点 $E^{*} = (T^{*}, L^{*}, I^{*}, V^{*}, C^{*})$ ，令方程右端项为0，可以得到以下方程组：

$\begin{array}{l} λ - d_{1} T^{*} - \frac{β T^{*} V^{*}}{1 + a V^{*}} = 0, \\ \frac{η β T^{*} V^{*}}{1 + a V^{*}} - α L^{*} - d_{2} L^{*} = 0, \\ \frac{(1 - η) β T^{*} V^{*}}{1 + a V^{*}} + α L^{*} - d_{3} I^{*} - p I^{*} C^{*} = 0, \\ k I^{*} - d_{4} V^{*} = 0, \\ q I^{*} - d_{5} C^{*} = 0, \end{array}$ (2-2)

CTL免疫细胞被激活条件下的感染平衡点为

$E^{*} = (\frac{λ d_{4} + a k I^{*} λ}{d_{1} d_{4} + a d_{1} k I^{*} + β k I^{*}}, \frac{β k I^{*} η λ}{(d_{1} d_{4} + a d_{1} k I^{*} + β k I^{*}) (α + d_{2})}, I^{*}, \frac{k I^{*}}{d_{4}}, \frac{q I^{*}}{d_{5}}) .$

将 $E^{*}$ 代入(2-2)的第三个方程中，令方程左端为可 $F (I^{*})$ 以得到

$\begin{matrix} F (I^{*}) = [\frac{- p q a k}{d_{5}} (β k + d_{1} a k)] I^{*}^{3} - [(d_{3} k^{2} a β + d_{3} k^{2} a^{2} d_{1}) + \frac{p q d_{4}}{d_{5}} (β k + d_{1} a k) + d_{1} d_{4} \frac{p q a k}{d_{5}}] I^{*}^{2} \\ - (d_{3} d_{4} β k + \frac{p q d_{4}^{2} d_{1}}{d_{5}}) I^{*} + d_{4} λ (1 - η) β k + \frac{η λ β k α}{α + d_{2}} \end{matrix}$

令 $I^{*} = 0$

$F (0) = d_{3} (\frac{(1 - η) β k λ}{d_{1} d_{3} d_{4}} + \frac{η α β k λ}{d_{1} d_{3} d_{4} (α + d_{2})} - 1) = d_{3} (R_{0} - 1),$

当 $R_{0} > 1$ 时， $F (0) > 0$ 。又由 $lim_{I \to + \infty} F (I^{*}) < 0$ 且

$\begin{matrix} F^{'} (I^{*}) = [\frac{- 3 p q a k}{d_{5}} (β k + d_{1} a k)] I^{*}^{2} - 2 [(d_{3} k^{2} α β + d_{3} k^{2} a^{2} d_{1}) + \frac{p q d_{4}}{d_{5}} (β k + d_{1} a k) + d_{1} d_{4} \frac{p q a k}{d_{5}}] I^{*} \\ - d_{3} d_{4} β k - \frac{p q d_{4}^{2} d_{1}}{d_{5}} \\ = - [\frac{3 p q a k}{d_{5}} (β k + d_{1} a k)] I^{*}^{2} - 2 [d_{3} k^{2} α β + d_{3} k^{2} a^{2} d_{1} + \frac{p q d_{4}}{d_{5}} (β k + d_{1} a k) + d_{1} d_{4} \frac{p q a k}{d_{5}}] I^{*} \\ - (d_{3} d_{4} β k + \frac{p q d_{4}^{2} d_{1}}{d_{5}}) \\ < 0, \end{matrix}$

可知， $F (I^{*})$ 是关于 $I^{*}$ 的单调递减函数，由零点定理可知方程 $F (I^{*}) = 0$ 在 $R_{0} > 1$ 时的正根存在且唯一，因此 $R_{0} > 1$ 时，模型(2-2)存在唯一的正平衡点。

3. 解的存在唯一性及非负性

定理4.1：当初始条件为 $T (0) \geq 0, L (0) \geq 0, I (0) \geq 0, V (0) \geq 0, C (0) \geq 0$ 时，模型(2-1)存在唯一的非负解。

证明：因为模型右端表达式是关于t的连续函数，且其一阶导数也是关于t的连续函数，由常微分方程组的存在唯一性定理可知，在初始条件下模型存在唯一解。下面，我们证明模型解的非负性。

由模型的第一个方程 ${\frac{d T}{d t} |}_{T = 0} = λ > 0$ ，又由 $T (0) \geq 0$ ，得对所有的 $t \geq 0$ 都有 $T (t) \geq 0$ 。

由模型的第二个方程 ${\frac{d L}{d t} |}_{L = 0} = \frac{η β T V}{1 + a V} > 0$ 。假设存在 $t_{1} = \inf {t | L (t) = 0, t > 0}$ ，使得 $\frac{d}{d t} L (t_{1}) = \frac{η β T (t_{1}) V (t_{1})}{1 + a V (t_{1})} \leq 0$ ，从而 $V (t_{1}) \leq 0$ ，由于 $V (0) \geq 0$ ，则存在 $t_{2} = \inf {t | V (t) = 0, t \in [0, t_{1})}$ ，使得 $\frac{d}{d t} V (t_{2}) \leq 0$ 。此时， $\frac{d}{d t} V (t_{2}) = k I (t_{2}) \leq 0$ ，由于 $I (0) \geq 0$ 则存在 $t_{3} = \inf {t | V (t) = 0, t \in [0, t_{2})}$ ，使得 $\frac{d}{d t} I (t_{3}) \leq 0$ 。因为 $\frac{d}{d t} I (t_{3}) = \frac{(1 - η) β T (t_{3}) V (t_{3})}{1 + a V (t_{3})} + α L (t_{3}) \leq 0$ ，所以 $L (t_{3}) < 0$ ，由于 $L (0) \geq 0$ ，则存在 $t_{4} = \inf {t | V (t) = 0, t \in [0, t_{3})}$ 。这与假设中定义的 $t_{2}$ 相矛盾，因此假设不成立。

于是 ${\frac{d L}{d t} |}_{L = 0} = \frac{η β T V}{1 + a V} > 0$ ，因为 $L (0) \geq 0$ ，则对所有 $t \geq 0$ 都有 $L (t) \geq 0$ ，有 ${\frac{d I}{d t} |}_{I = 0} = \frac{(1 - η) β T V}{1 + a V} + α L > 0$ 。又因为 $I (0) \geq 0$ ，则对所有 $t \geq 0$ 都有 $I (t) \geq 0$ ，所以有 ${\frac{d V}{d t} |}_{V = 0} = k I > 0$ 。又因为 $V (0) \geq 0$ ，则对所有 $t \geq 0$ 都有 $V (t) \geq 0$ ，所以 ${\frac{d C}{d t} |}_{C = 0} = q I > 0$ 。又因为 $C (0) \geq 0$ ，则对所有 $t \geq 0$ 都有 $C (t) \geq 0$ 。由此可得该唯一的解非负。

综上所述，模型(2-1)的解满足存在唯一性和非负性。

4. 平衡点的稳定性

首先考虑模型(2-1)在平衡点 $E = (\tilde{T}, \tilde{L}, \tilde{I}, \tilde{V}, \tilde{C})$ 的情况，计算其雅克比矩阵 [5] 为

$J (E) = [\begin{matrix} - d_{1} - \frac{β \tilde{V}}{1 + a \tilde{V}} & 0 & 0 & \frac{- β \tilde{T}}{{(1 + a \tilde{V})}^{2}} & 0 \\ \frac{η β \tilde{V}}{1 + a \tilde{V}} & - α - d_{2} & 0 & \frac{η β \tilde{T}}{{(1 + a \tilde{V})}^{2}} & 0 \\ \frac{(1 - η) β \tilde{V}}{1 + a \tilde{V}} & α & - d_{3} - p \tilde{C} & \frac{(1 - η) β \tilde{T}}{{(1 + a \tilde{V})}^{2}} & - p \tilde{I} \\ 0 & 0 & k & - d_{4} & 0 \\ 0 & 0 & q & 0 & - d_{5} \end{matrix}] .$

定理4.1 当 $R_{0} < 1$ 时，未感染平衡点 $E_{0}$ 是局部渐近稳定的；当 $R_{0} > 1$ 时，未感染平衡点 $E_{0}$ 是不稳定的。

证明：模型(2-1)在未感染平衡点 $E_{0} = (\frac{λ}{d_{1}}, 0, 0, 0, 0)$ 处的雅克比矩阵为

$J (E_{0}) = [\begin{matrix} - d_{1} & 0 & 0 & \frac{- β λ}{d_{1}} & 0 \\ 0 & - α - d_{2} & 0 & \frac{η β λ}{d_{1}} & 0 \\ 0 & α & - d_{3} & \frac{(1 - η) β λ}{d_{1}} & 0 \\ 0 & 0 & k & - d_{4} & 0 \\ 0 & 0 & q & 0 & - d_{5} \end{matrix}],$

得特征方程

$(ζ + d_{1}) (ζ + d_{4}) (ζ + d_{5}) g (ζ) = 0,$

$g (ζ) = ζ^{3} + a_{1} ζ^{2} + a_{2} ζ + a_{3},$

其中，

$a_{1} = \frac{d_{1} d_{3} + d_{1} α + d_{1} d_{2} + d_{1} d_{4}}{d_{1}} > 0,$

$a_{2} = \frac{d_{1} d_{4} α + d_{1} d_{2} d_{4} + d_{1} d_{3} (α + d_{2} + d_{4}) - k β λ (1 - η)}{d_{1}},$

$a_{3} = \frac{(α + d_{2}) d_{1} d_{3} d_{4}}{d_{1}} - [α + (1 - η) d_{2}] k β λ = \frac{(1 - R_{0}) d_{1} d_{3} d_{4} (α + d_{2})}{d_{1}},$

而通过观察我们已得出 $ζ_{1} = - d_{1} < 0$ ， $ζ_{2} = - d_{4} < 0$ ， $ζ_{3} = - d_{5} < 0$ 。

而根据上式对 $a_{3}$ 化简，我们可以发现在 $R_{0} < 1$ 时， $a_{3} > 0$ 恒成立。且

$H_{1} = a_{1} > 0,$

$\begin{matrix} H_{2} = | \begin{matrix} a_{1} & a_{3} \\ 0 & a_{2} \end{matrix} | = a_{1} a_{2} - a_{3} \\ = (d_{3} + d_{4}) d_{3} d_{4} + α d_{2} {(d_{3} + d_{4})}^{2} + \frac{k β λ (η - 1) (d_{3} + d_{4})}{d_{1}} \\ + α d_{2} (d_{3} + d_{4}) (α + d_{2}) + \frac{α k η β λ}{d_{1}} \\ > 0, \end{matrix}$

$H_{3} = | \begin{matrix} a_{1} & a_{3} & 0 \\ 1 & a_{2} & 0 \\ 0 & a_{1} & a_{0} \end{matrix} | = a_{3} H_{2} > 0,$

故由Routh-Hurwitz判据 [6] 可知，特征方程的根具有负实部。在 $R_{0} < 1$ 时，未感染平衡点具有局部渐近稳定性。

当 $R_{0} > 1$ 时， $a_{3} < 0$ ，而当 $ζ \to + \infty$ 时， $g (ζ) > 0$ ；当 $ζ = 0$ 时， $g (ζ) = a_{3} < 0$ ，由零点定理可知 $g (ζ)$ 至少有一个正根。因此在 $R_{0} > 1$ 时，未感染平衡点是不稳定的。定理得证。

定理4.2 当 $R_{0} > 1$ 且 $H_{4} > 0$ 时，感染平衡点 $E^{*}$ 是局部渐近稳定的。

证明：通过将平衡点 $E^{*} = (T^{*}, L^{*}, I^{*}, V^{*}, C^{*})$ 处的雅克比矩阵由特征方程式 $| ξ E - J (E^{*}) | = 0$ 表示，可以得到：

$| \begin{matrix} ξ + d_{1} + \frac{β V^{*}}{1 + a V^{*}} & 0 & 0 & \frac{β T^{*}}{{(1 + a V^{*})}^{2}} & 0 \\ \frac{- η β V^{*}}{1 + a V^{*}} & ξ + α + d_{2} & 0 & - \frac{η β T^{*}}{{(1 + a V^{*})}^{2}} & 0 \\ \frac{(η - 1) β V^{*}}{1 + a V^{*}} & - α & ξ + d_{3} + p C^{*} & \frac{(η - 1) β T^{*}}{{(1 + a V^{*})}^{2}} & p I^{*} \\ 0 & 0 & - k & ξ + d_{4} & 0 \\ 0 & 0 & - q & 0 & ξ + d_{5} \end{matrix} |,$

进一步得出特征方程

$(ζ + d_{1}) (ζ + d_{4}) (ζ + d_{5}) h (ζ) = 0,$

$h (ζ) = ζ^{5} + b_{1} ζ^{4} + b_{2} ζ^{3} + b_{3} ζ^{2} + b_{4} ζ + b_{5} .$

其中

$b_{1} = d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + \frac{β V^{*}}{1 + a V^{*}} + α + p C^{*} > 0,$

$\begin{matrix} b_{2} = - (1 - η) \frac{k β T^{*}}{{(1 + a V^{*})}^{2}} + (d_{4} + d_{5}) (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) + d_{4} d_{5} + (α + d_{2} + d_{3} + p C^{*}) (d_{1} + \frac{β V^{*}}{1 + a V^{*}} + d_{4} + d_{5}) \\ + (d_{3} + p C^{*}) (α + d_{2}), \end{matrix}$

$\begin{matrix} b_{3} = [d_{2} η - d_{2} - α - (d_{1} + d_{5}) (1 - η)] \frac{k β T^{*}}{{(1 + a V^{*})}^{2}} + (d_{1} + d_{2} + d_{4} + α + \frac{β V^{*}}{1 + a V^{*}}) q p I^{*} \\ + (α + d_{2} + d_{3} + p C^{*}) [(d_{4} + d_{5}) (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) + d_{4} d_{5}] + d_{4} d_{5} (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) \\ + (d_{1} + d_{4} + d_{5} + \frac{β V^{*}}{1 + a V^{*}}) (d_{3} + p C^{*}) (d_{2} + α), \end{matrix}$

$\begin{matrix} b_{4} = [(d_{1} + d_{5}) (d_{2} η - d_{2} - α) - d_{1} d_{5} (1 - η)] \frac{k β T^{*}}{{(1 + a V^{*})}^{2}} \\ + {(α + d_{2} + d_{3} + p C^{*}) d_{4} d_{5} (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) + (d_{3} + p C^{*}) (α + d_{2}) [(d_{4} + d_{5}) (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) + d_{4} d_{5}]} \\ + [d_{1} d_{4} + d_{4} \frac{β V^{*}}{1 + a V^{*}} + (α + d_{2}) (d_{1} + d_{4} + \frac{β V^{*}}{1 + a V^{*}})] q p I^{*}, \end{matrix}$

$\begin{matrix} b_{5} = d_{1} d_{5} (d_{2} η - d_{2} - α) \frac{k β T^{*}}{{(1 + a V^{*})}^{2}} + (d_{3} + p C^{*}) (α + d_{2}) d_{4} d_{5} (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) \\ + (α + d_{2}) (d_{1} d_{4} + d_{4} \frac{β V^{*}}{1 + a V^{*}}) q p I^{*}, \end{matrix}$

而通过观察我们已得出 $ζ_{1} = - d_{1} < 0$ ， $ζ_{2} = - d_{4} < 0$ ， $ζ_{3} = - d_{5} < 0$ ，且

$H_{1} = b_{1} > 0,$

$\begin{array}{l} H_{2} = b_{1} b_{2} - b_{3} \\ = (d_{1} + \frac{β V^{*}}{1 + a V^{*}} + d_{2} + d_{3} + d_{4} + d_{5} + α + p C^{*}) \times [(1 - η) \frac{k β T^{*}}{{(1 + a V^{*})}^{2}} + (d_{4} + d_{5}) (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) \\ + d_{4} d_{5} + (α + d_{2} + d_{3} + p C^{*}) (d_{1} + \frac{β V^{*}}{1 + a V^{*}} + d_{2} + d_{3}) + (d_{3} + p C^{*}) (α + d_{2}) + q p I^{*}] \\ + [(d_{1} + d_{5}) (1 - η) + d_{2} (1 - η) + α] \frac{k β T^{*}}{{(1 + a V^{*})}^{2}} - (d_{1} + d_{2} + d_{4} + α + \frac{β V^{*}}{1 + a V^{*}}) q p I^{*} \\ - (α + d_{2} + d_{3} + p C^{*}) [(d_{4} + d_{5}) (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) + d_{4} d_{5}] - d_{4} d_{5} (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) \end{array}$

$\begin{array}{l} - (d_{1} + \frac{β V^{*}}{1 + a V^{*}} + d_{4} + d_{5}) (d_{3} + p C^{*}) (α + d_{2}) \\ = (\frac{β V^{*}}{1 + a V^{*}} + d_{3} + d_{4} + p C^{*}) (1 - η) \frac{k β T^{*}}{{(1 + a V^{*})}^{2}} + (d_{1} + \frac{β V^{*}}{1 + a V^{*}} + d_{4} + d_{5}) [(d_{4} + d_{5}) (d_{1} + \frac{β V^{*}}{1 + a V^{*}}) + d_{4} d_{5}] \\ + (d_{1} + \frac{β V^{*}}{1 + a V^{*}} + d_{2} + d_{3} + d_{4} + d_{5} + α + p C^{*}) (α + d_{2} + d_{3} + p C^{*}) (d_{1} + \frac{β V^{*}}{1 + a V^{*}} + d_{4} + d_{5}) \\ + (d_{2} + d_{3} + α + p C^{*}) (d_{3} + p C^{*}) (α + d_{2}) + (d_{3} + d_{5} + p C^{*}) q p I^{*} \\ > 0, \end{array}$

$\begin{array}{l} H_{3} = b_{3} | \begin{matrix} b_{1} & b_{3} \\ 1 & b_{2} \end{matrix} | - b_{1} | \begin{matrix} b_{1} & b_{5} \\ 1 & b_{4} \end{matrix} | \\ = b_{3} (b_{1} b_{2} - b_{3}) - b_{1} (b_{1} b_{4} - b_{5}) \\ = {[(α + d_{2}) (d_{4} (d_{3} + d_{5} + p C) + d_{5} (2 p C + d_{3})) + d_{4} d_{5} (d_{3} + 2 p C)] \begin{matrix} \end{matrix} \\ + [d_{4} (d_{3} + d_{5} + p C) + d_{5} (2 p C + d_{3}) + (d_{2} + α) (d_{3} + d_{4} + d_{5} + p C)] (d_{1} + \frac{β V}{1 + a V}) \\ - [α + (1 - η) (d_{1} + d_{2} + d_{5})] \frac{β T k}{{(1 + a V)}^{2}}} \end{array}$

$\begin{array}{l} \times {(d_{3} + d_{5} + p C) [(α + d_{2}) (d_{2} + d_{3} + d_{5} + p C + α) + d_{4} (d_{2} + d_{3} + d_{4} + d_{5} + p C + α)] \begin{matrix} \end{matrix} \\ + (2 p C + d_{3}) d_{5} [d_{2} + d_{3} + d_{4} + d_{5} + p C + α + (d_{1} + \frac{β V}{1 + a V}) (1 - α - d_{2} - d_{4})] \\ + (d_{2} + α) d_{4} (d_{2} + d_{3} + d_{5} + p C + α) + (d_{1} + d_{2} + d_{3} + d_{5} + p C + α + \frac{β V}{1 + a V}) \\ (d_{1} + \frac{β V}{1 + a V}) (d_{2} + d_{3} + d_{5} + p C + α) + \frac{β T k}{{(1 + a V)}^{2}} [α + (1 - η) (- d_{3} - p C - α - \frac{β V}{1 + a V})]} \\ - {[d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + p C + α + \frac{β V}{1 + a V}]}^{2} \times (d_{1} + \frac{β V}{1 + a V}) \end{array}$

$\begin{array}{l} [(d_{2} + α) (d_{4} (d_{3} + d_{5} + p C) + d_{5} (d_{3} + 2 p C)) + d_{4} d_{5} (d_{3} + 2 p C)] \\ + (d_{2} + d_{3} + d_{4} + d_{5} + p C + α) d_{4} d_{5} (d_{2} + α) (d_{3} + 2 p C) - [d_{2} + d_{3} + d_{4} + d_{5} + p C + α + d_{1} + \frac{β V}{1 + a V}] \\ \times {d_{5} [α + d_{2} (1 - η)] + d_{1} [α + (1 - η) (d_{2} + d_{5})]} \frac{β T k}{{(1 + a V)}^{2}} + d_{2} d_{5} [d_{2} (1 - η) + α] \frac{β T k}{{(1 + a V)}^{2}} \end{array}$

$\begin{array}{l} = {(d_{3} + 2 p C) d_{5} (α + d_{1} + d_{2} + d_{4} + \frac{β V}{1 + a V}) + (α + d_{2}) (d_{3} + d_{5} + p C) (d_{1} + d_{4} + \frac{β V}{1 + a V}) \\ + d_{4} (d_{2} + d_{3} + d_{5} + p C + α) (d_{1} + \frac{β V}{1 + a V}) + (α + d_{2}) (d_{2} + d_{3} + d_{5} + p C + α)} \times {(d_{2} + d_{3} + d_{5} + p C + α) \begin{matrix} \end{matrix} \\ [(α + d_{2}) (d_{2} + d_{3} + d_{5} + p C + α)] + (d_{2} + d_{3} + d_{5} + p C + α) [(d_{3} + 2 p C) d_{5} + {(d_{1} + \frac{β V}{1 + a V})}^{2} \\ \begin{matrix} \end{matrix} + d_{4} (d_{2} + d_{3} + d_{5} + p C + α)] + (d_{1} + \frac{β V}{1 + a V}) [(d_{3} + 2 p C) d_{5} (1 + α + d_{2} + d_{4}) + {(d_{2} + d_{3} + d_{4} + d_{5} + p C + α)}^{2}] \end{array}$

$\begin{array}{l} + \frac{β T k}{{(1 + a V)}^{2}} [α + (1 - η) (+ d_{3} + d_{4} + p C + α + \frac{β V}{1 + a V})]} + {(d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + p C + α + \frac{β V}{1 + a V})}^{2} \\ \times (d_{1} + \frac{β V}{1 + a V}) [(α + d_{2}) d_{4} (d_{3} + d_{5} + p C) + (d_{3} + 2 p C) d_{5} + (d_{3} + 2 p C) d_{4} d_{5}] + d_{4} d_{5} (d_{2} + d_{3} + d_{4} + d_{5} + p C + α) \\ (α + d_{2}) (d_{3} + 2 p C) (d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + p C + α + \frac{β V}{1 + a V}) + \frac{β T k}{{(1 + a V)}^{2}} (d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + p C + α + \frac{β V}{1 + a V}) \\ {(1 - η) (d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + p C + α + \frac{β V}{1 + a V}) [d_{2} d_{5} + d_{1} (d_{2} + d_{5})] + d_{1} d_{5} [α + d_{2} (1 - η)]} \\ > 0, \end{array}$

$H_{4} = b_{4} H_{3} - b_{5} (b_{1} b_{2}^{2} + b_{5} - b_{2} b_{3} - b_{1} b_{4}),$

$H_{5} = b_{5} H_{4},$

故由Routh-Hurwitz判据可知，特征方程具有负实部的根。在 $R_{0} > 1$ 且 $H_{4} > 0$ 时，感染平衡点是局部渐近稳定的。定理得证。

5. 数值模拟

5.1. 模型数值模拟

参考文献 [7] 是基于CTL免疫的HIV感染模型研究，文献 [8] 是通过病毒动力学模型研究HIV感染治疗，两篇文献都提供了本文需要的部分参数范围及数据取值。因此结合文献 [7] 与文献 [8] 的数据，在本部分中进行整理，将参数的含义、单位及其取值范围，以数值模拟所取的参数值形式在列表1显示。

Table 1. The meaning and value of the parameters in the model (2-1)

表1. 模型(2-1)中参数的含义与取值

研究未感染平衡点的局部渐近稳定性。

首先，代入参数表1中的Data 1可计算得到基本再生数 $R_{0} = 0.5442 < 1$ 。其次，通过Matlab进行数值模拟，其中初值选取为 $T (0) = 2000, L (0) = 0.001, I (0) = 0.001, V (0) = 0.001, C (0) = 0.001$ ，计算未感染的细胞个数T = 1145.52，模拟结果如图1所示，不难看出，模型(2-1)的数值模拟结果趋于未感染平衡点 $E_{0}$ ，符合定理4.1未感染平衡点 $E_{0}$ 的局部渐近稳定性。

接下来研究感染平衡点的局部渐近稳定性。首先，代入参数表1中的Data 2可计算得到基本再生数 $R_{0} = 7.7129 > 1$ ，且经过验证满足定理4.2中的充分条件H₄ > 0。其次，通过Matlab数值模拟，其初值同样选取为 $T (0) = 2000, L (0) = 0.001, I (0) = 0.001, V (0) = 0.001, C (0) = 0.001$ ，模拟结果如图2所示。不难看出，模型(2-1)的数值模拟结果趋于未感染平衡点 $E^{*}$ ，符合定理4.2感染平衡点 $E^{*}$ 的局部渐近稳定性。

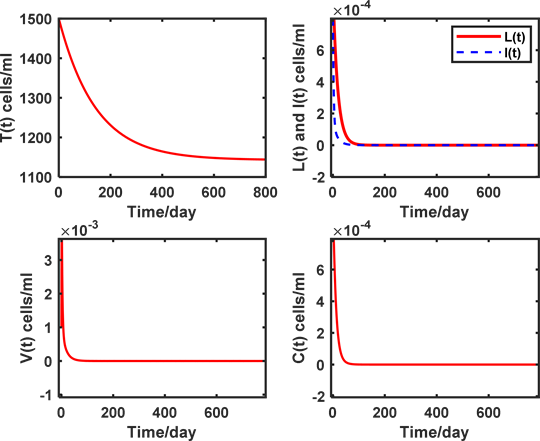
Figure 1. The local asymptotic stability of the uninfected equilibrium of the model (2-1)

图1. 模型(2-1)的未感染平衡点的局部渐近稳定性

Figure 2. The local asymptotic stability of the infected equilibrium of the model (2-1)

图2. 模型(2-1)的感染平衡点的局部渐近稳定性

5.2. 模型比较

当模型(2-1)不考虑潜伏感染的T细胞的情况时，HIV的感染动力学模型为：

$\begin{array}{l} \frac{d T}{d t} = λ - d_{1} T - \frac{β T V}{1 + a V}, \\ \frac{d I}{d t} = \frac{β T V}{1 + a V} - d_{3} I - p I C, \\ \frac{d V}{d t} = k I - d_{4} V, \\ \frac{d C}{d t} = q I - d_{5} C . \end{array}$ (5-1)

接下来利用数值模拟分析模型(2-1)和模型(5-1)的差异。为了使模型比较拥有较好的结果，选取代入参数表1中的Data 2，初值为 $T (0) = 1000, I (0) = 0.001, V (0) = 0.001, C (0) = 0.001$ 。运用Matlab软件进行操作，结果如图3所示。可得出结论，若受潜伏时期影响，受感染的CD4⁺T细胞的浓度、血液里病毒粒子的浓度将以更慢的速度达到稳定趋于零的状态，而在t时刻未受HIV病毒感染的CD4⁺ T细胞的浓度与CTL细胞的浓度具有相近的变化趋势。这说明潜伏模型会延长人体感染病毒的时间，而对感染病毒的细胞浓度无明显影响。

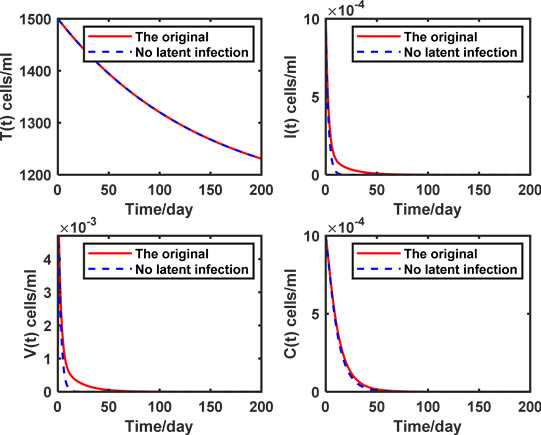
Figure 3. The comparison results of model (2-1) and model (5-1)

图3. 模型(2-1)和模型(5-1)的比较结果

当模型(2-1)不考虑免疫应答的情况时，HIV的感染动力学模型为：

$\begin{array}{l} \frac{d T}{d t} = λ - d_{1} T - \frac{β T V}{1 + a V}, \\ \frac{d L}{d t} = \frac{η β T V}{1 + a V} - α L - d_{2} L, \\ \frac{d I}{d t} = \frac{(1 - η) β T V}{1 + a V} + α L - d_{3} I, \\ \frac{d V}{d t} = k I - d_{4} V . \end{array}$ (5-2)

接下来利用数值模拟分析模型(2-1)和模型(5-2)的差异。为了使模型比较拥有较好的结果，选取代入参数表1中的Data 2，初值为 $T (0) = 1000, I (0) = 0.001, V (0) = 0.001, C (0) = 0.001$ 。利用Matlab软件进行操作，结果如图4。从图中可以看出，受免疫应答的影响，血液里病毒粒子的浓度与CTL细胞的浓度到达的峰值更低，同时会以更快的速度达到稳定趋于零的状态，而在t时刻未受HIV病毒感染的CD4⁺ T细胞的浓度与受感染的CD4⁺ T细胞的浓度具有相近的变化趋势，免疫应答影响不大。

Figure 4. The comparison results of model (2-1) and model (5-2)

图4. 模型(2-1)和模型(5-2)的比较结果

6. 结语

本文在考虑潜伏感染和免疫应答这两种生物学机理的基础上，首先通过建立基于饱和发生率的HIV感染模型，并求解得到模型的未感染和感染平衡点，并通过推导定义基本在生数 $R_{0}$ ，然后通过微分方程稳定性理论证明得在 $R_{0} < 1$ 时未感染平衡点具有局部渐近稳定性，当 $R_{0} > 1$ 时感染平衡点具有局部渐近稳定性。最后为验证平衡点的稳定性，我们对所建模型进行了数值模拟，并将所建模型与相关模型进行对比，以此得到模型与理论分析的正确性，为疾病控制中心和临床试验者提供病情监测和数据收集的定量依据。后人也可以在此模型的基础上考虑时滞等因素的影响，以此对模型进行进一步的丰富和完善。

基金项目

中国石油大学(华东)大学生创新创业训练计划资助项目(202012045)

文章引用

宋世杰,陈莺蓉,李朋朔,王艳. 基于潜伏感染和饱和发生率的HIV感染模型
An HIV Infection Model Based on Latent Infection and Saturated Incidence Rate[J]. 应用数学进展, 2022, 11(05): 2900-2912. https://doi.org/10.12677/AAM.2022.115308

参考文献

1. 孙起麟. 艾滋病病毒感染和治疗动力学的理论研究与应用[D]: [博士学位论文]. 北京: 北京科技大学, 2015.

2. 黎静. HIV感染模型的动力学分析[D]: [硕士学位论文]. 长沙: 湖南大学, 2012.

3. 杜百知. 具有潜伏细胞的HIV感染模型的动力学分析[D]: [硕士学位论文]. 衡阳: 南华大学, 2017.

4. 张剑锋, 李玉闽. CTL免疫反应的HIV感染模型的动力学分析[J]. 漳州师范学院学报(自然科学版), 2009, 22(1): 30-34.

5. 雷学红, 许云霞. 具有时滞和免疫反应的离散HIV感染模型的稳定性分析[J]. 湖北民族大学学报(自然科学版), 2021, 39(3): 291-298.

6. Chen, W., Tuerxun, N. and Teng, Z.D. (2020) The Global Dynamics in a Wild-Type and Drug-Resistant HIV Infection Model with Saturated Incidence. Advances in Difference Equations, 2020, Article No. 25. https://doi.org/10.1186/s13662-020-2497-2

7. Wang, Y., Zhou, Y.C., Brauer, F. and Heffernan, J.M. (2013) Viral Dynamics Model with CTL Immune Response Incorporating Antiretroviral Therapy. Journal of Mathematical Bi-ology, 67, 901-934. https://doi.org/10.1007/s00285-012-0580-3

8. Hill, A.L., Rosenbloom, D.I.S., Nowak, M.A. and Siliciano, R.F. (2018) Insight into Treatment of HIV Infection from Viral Dynamics Models. Immunological Reviews, 285, 9-25. https://doi.org/10.1111/imr.12698

期刊菜单