Pure Mathematics
Vol.04 No.04(2014), Article ID:13855,7
pages
10.12677/PM.2014.44020
The Recursive Formula of Two Kinds of Formal Power Series
Yanli Chen, Wanhui Ji
Yinchuan Energy Institute, Yinchuan
Email: chenyanli8866.hi@163.com
Received: Jun. 10th, 2014; revised: Jul. 8th, 2014; accepted: Jul. 16th, 2014
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
By using the trigonometric function, the hyperbolic function and the series expansion of their product, the expansions and the recursive formula of these two forms of power series [ (
(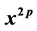 ’s ratio of secx series) and
’s ratio of secx series) and 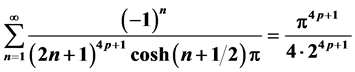 (
(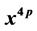 ’s ratio of secxsechx series )] are derived. At the same time, we prove them one by one using the residue theorem.
’s ratio of secxsechx series )] are derived. At the same time, we prove them one by one using the residue theorem.
Keywords:Series of Trigonometric Function, Formal Power Series, Recursive Formula, Residue Theorem

两类形式幂级数的 递推公式
陈艳丽,及万会
银川能源学院,银川
Email: chenyanli8866.hi@163.com
收稿日期:2014年6月10日;修回日期:2014年7月8日;录用日期:2014年7月16日

摘 要
应用三角函数、双曲函数以及二者乘积的级数展开式,推导出两个形式幂级数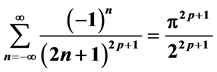 [级数
[级数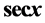 中
中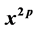 的系数]和
的系数]和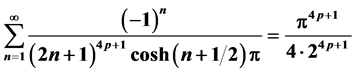 [级数
[级数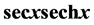 中
中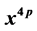 的系数]的展开式及递推公式,并应用留数基本定理逐一作出证明。
的系数]的展开式及递推公式,并应用留数基本定理逐一作出证明。
关键词 :三角函数的级数,形式幂级数,递推公式,留数定理

1. 引言
三角函数和双曲函数二者的级数,通常在研究数论的一些问题时需要用到。王欣[1] 应用Cauchy留数定理、部分分式、形式幂级数和超几何级数等经典分析方法,研究了含自由参数的三角函数恒等式、有限三角和的封闭公式以及其它类型的三角和恒等式等组合计算问题。及万会,吴永[2] 针对双曲函数方幂和做了一定的研究。
在此基础上,本文首先应用三角函数、双曲函数的以及二者乘积的级数展开式推导出形式幂级数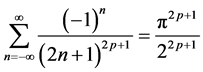 [级数
[级数 中
中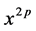 的系数]的表达式,并且得到了一个表达形式较为简单的递推公式。同时应用此方法求得形式幂级数
的系数]的表达式,并且得到了一个表达形式较为简单的递推公式。同时应用此方法求得形式幂级数 。
。
[级数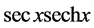 中
中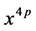 的系数]的表达式和递推公式,并应用留数基本定理逐一作出证明。
的系数]的表达式和递推公式,并应用留数基本定理逐一作出证明。
引理1[3] :三角函数展开成级数如下(用数学软件maple13展开)
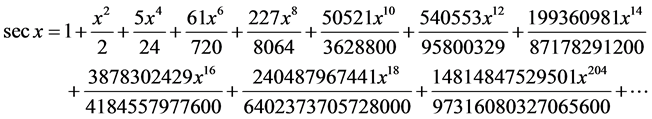 (1)
(1)
 (2)
(2)
所以
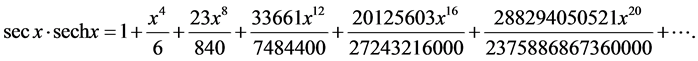 (3)
(3)
引理2[4] [5] :(留数基本定理)如果函数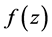 在扩充复平面内只有有限个奇点,那么
在扩充复平面内只有有限个奇点,那么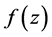 在所有各奇点(包括
在所有各奇点(包括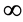 点)的留数总和必等于零。
点)的留数总和必等于零。
2. 和式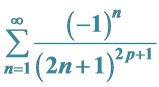 的计算
的计算
2.1. 考虑围线积分
如图1所示,取矩形区域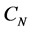 ,顶点
,顶点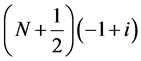 ,
,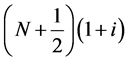 ,
,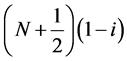 和
和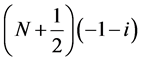 。
。
图1表示,当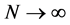 时,函数
时,函数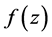 在复平面内向四周无限扩充,根据引理[2] ,
在复平面内向四周无限扩充,根据引理[2] ,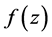 在所有各奇点(包括
在所有各奇点(包括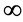 点)的留数总和必等于零。
点)的留数总和必等于零。

Figure 1. Rectangular area in the complex plane
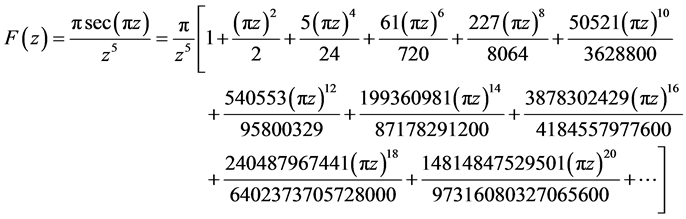
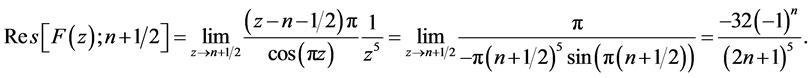
从而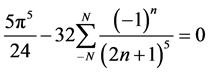 ,
,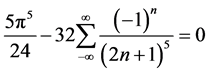 ,
,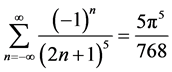 。
。
2.3. 考虑围线积分
函数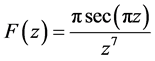 在
在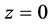 是7阶极点,在单极点
是7阶极点,在单极点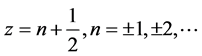 。
。
由级数(1)令 ,那么级数
,那么级数
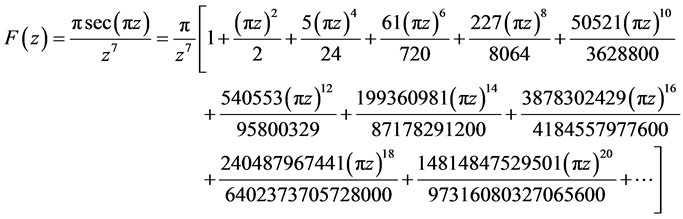
级数式中项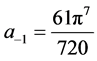 ,于是在
,于是在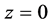 ,
,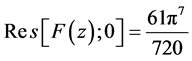 ;而
;而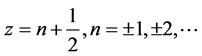 ,
,
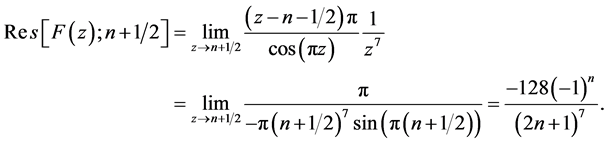
由图1以及引理2可知,当 时,围线积分
时,围线积分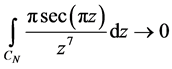
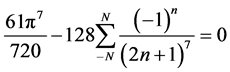 ,
,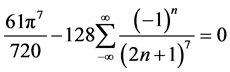 ,
,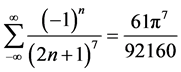 。
。
同法利用级数(1)可得到
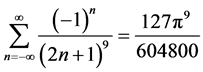 ;
;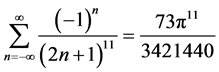 ;
;
 ;
;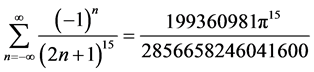 。
。
结论1: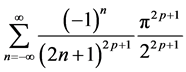 [级数
[级数 中
中 的系数]。
的系数]。
3. 和式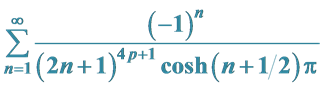 计算
计算
3.1. 考虑围线积分
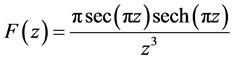 在
在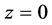 是5阶极点;单极点
是5阶极点;单极点 。
。
单极点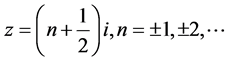 。由级数(3)令
。由级数(3)令 ,那么级数
,那么级数
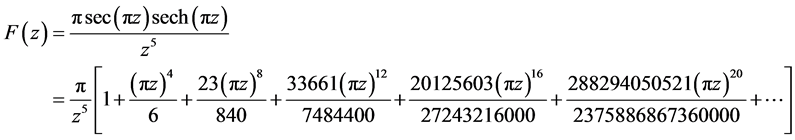
级数式中项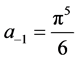 ,从而
,从而
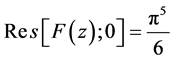 ,
,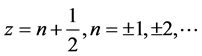 ,
,
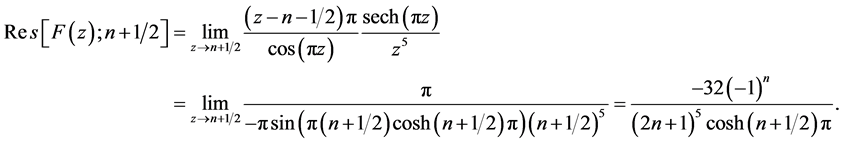
在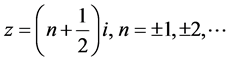
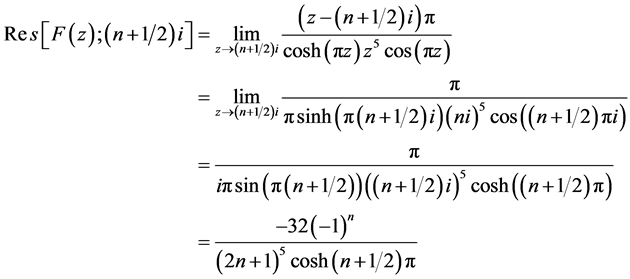
由图1以及引理2可知,当 时,围线积分
时,围线积分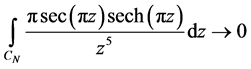
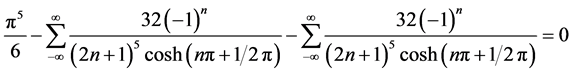 ;
;
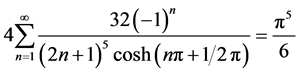 ,
,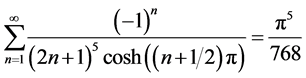
3.2. 考虑围线积分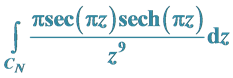
函数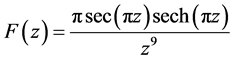 在
在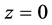 是9阶极点;单极点
是9阶极点;单极点 。
。
单极点 。由级数(3)令
。由级数(3)令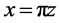 ,那么级数
,那么级数

级数式中项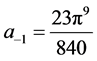 ,在
,在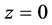 ,从而
,从而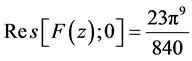 ,单极点
,单极点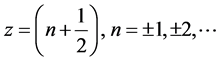 。
。
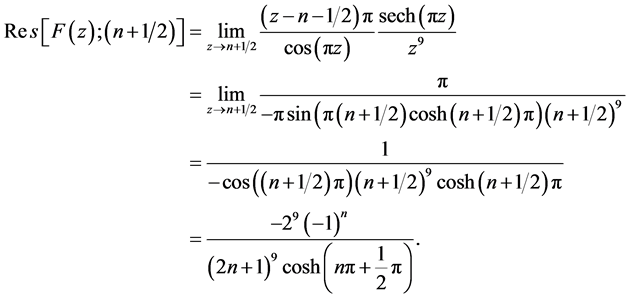
单极点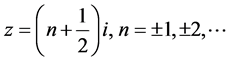 。
。
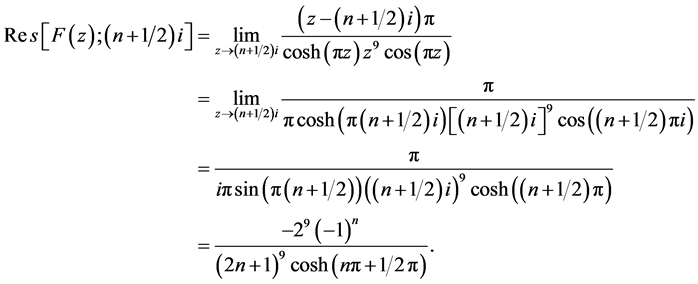
由图1以及引理2可知,当 时,围线积分
时,围线积分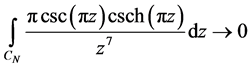 ,
,
从而
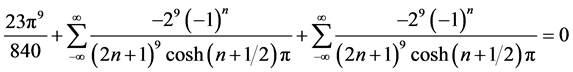 ;
;
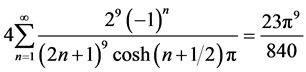 ,
,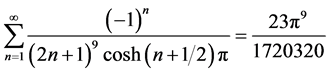
3.3. 考虑围线积分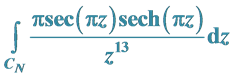
函数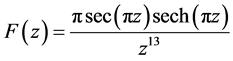 在
在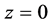 是13阶极点;单极点
是13阶极点;单极点 。
。
单极点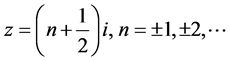 。由级数(3)令
。由级数(3)令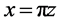 ,那么级数
,那么级数
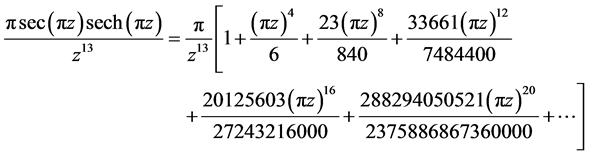
级数式中项 ,在
,在 ,从而
,从而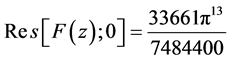 ,
,
在单极点
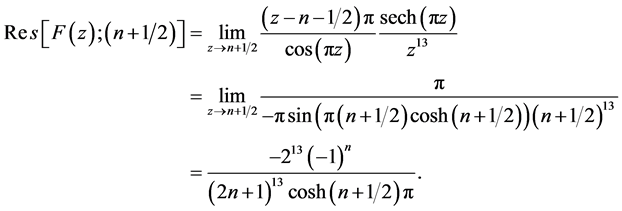
单极点 。
。
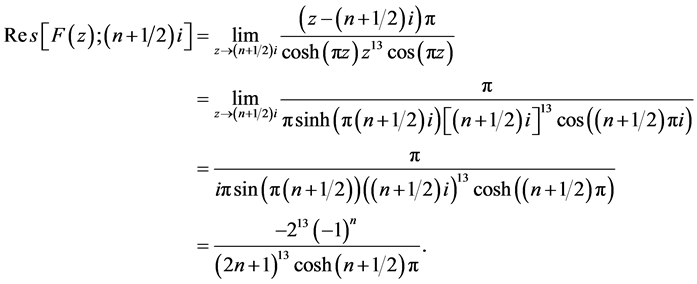
由图1以及引理2可知,当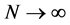 时,围线积分
时,围线积分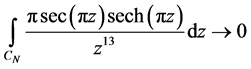 ,
,
从而
 ;
;
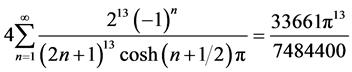 ,
,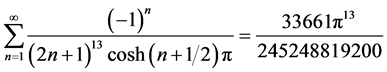
同法利用级数(3)可得如下
 ;
;
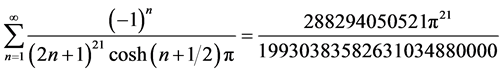 。
。
结论2: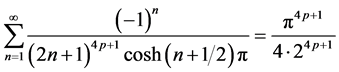 [级数
[级数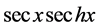 中
中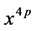 的系数]。
的系数]。
基金项目
银川能源学院科研项目基金(2012-KY-P-31)。
文章引用
陈艳丽,及万会, (2014) 两类形式幂级数的递推公式
The Recursive Formula of Two Kinds of Formal Power Series. 理论数学,04,130-137. doi: 10.12677/PM.2014.44020
参考文献 (References)
- 1. 王欣, D. (2007) 有限三角函数和的经典分析方法. 大连理工大学, 大连.
- 2. 及万会, 吴永 (2011) J.双曲函数方幂和. 纺织高校基础科学学报, 2, 246-249.
- 3. Gradshteyn, I.S. and Zyzhik I.M. (1965) A table of integral, series and products. Academic Press is an Imprint of Elsevier, 7th Edition, Academic Press, New York, 42-43.
- 4. 盖云英, 包革军, M. (2007) 复变函数与积分变换. 第2版, 科学出版社, 北京, 127-128.
- 5. 雷鹏, 郭锂, J. (2013) 多重Zeta偶数值的六重求和公式. 兰州大学学报(自然科学版), 1, 100-102.
- 6. Tom, M. and Apostoil, M. (1976) Introduction to Analytic Number Theory. New York Inc., Spring-Verluy, 55.