Pure Mathematics
Vol.04 No.06(2014), Article ID:14391,9
pages
10.12677/PM.2014.46037
Solitary Waves of Singularly Perturbed KdV-KS Equation with Distributed Delay
Yongxin Jiang
College of Science, Hohai University, Nanjing
Email: yxinjiang@126.com
Received: Oct. 13th, 2014; revised: Nov. 10th, 2014; accepted: Nov. 14th, 2014
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
We study a sort of nonlinear reaction diffusion equation based on the Korteweg-de Vries (KdV) equation with a convolution term which introduces a time delay in the nonlinearity and with a higher order singularly perturbing term as the Kuramoto-Sivashinsky (KS) equation, called KdV-KS equation. We focus on the question of the existence of solitary wave solutions. By using geometric singular perturbation analysis and the linear chain trick, we prove that the solitary wave solutions persist when the average delay is suitably small. The explicit expression of original KdV solitary is not required.
Keywords:Geometric Singular Perturbation, KdV Equation, Solitary Wave, Distributed Delay
具有分布时滞的奇异扰动KdV-KS方程的孤立波
蒋永新
河海大学理学院,南京
Email: yxinjiang@126.com
收稿日期:2014年10月13日;修回日期:2014年11月10日;录用日期:2014年11月14日

摘 要
我们研究一类基于KdV方程的非线性反应扩散方程,其非线性项具有分布时滞,高阶项是奇异扰动项,即著名的KS条件,我们称之为KdV-KS方程。我们主要研究孤立波的存在性,通过运用几何奇异摄动和线性链的技巧,证明了当平均时滞适当小时孤立波解的保持性,这里我们不需要原始KdV方程孤立波解的显式表达式。
关键词 :几何奇异摄动,KdV方程,孤立波,分布时滞

1. 引言
Korteweg de Vries方程(简称KdV方程)
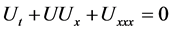 (1)
(1)
是研究浅水波运动的一个一维数学模型,它是1895年由荷兰数学家Diederik Korteweg和Gustav de Vries [1] 共同发现的。KdV方程的研究一直是一个非常丰富,有趣和活跃的数学领域。特别值得提出的是,它是一个能写出精确解的非线性偏微分方程。KdV方程可以用逆散射变换求解,也可以用Darboux变换,Lie群方法等求解 [2] [3] 。近年来,很多学者关心扰动KdV方程,特别是高阶项是奇异扰动的KS方程。即KdV-KS方程。
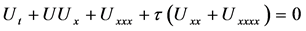 (2)
(2)
Ercolani [4] 研究了其周期解,T. Ogawa [5] 研究了其同宿轨和孤立波,范兴华等 [6] 分析了具有更复杂非线性项的mKdV-KS方程,用的主要方法是几何奇异摄动理论 [7] [8] 。这种方法也用来分析其他的反映扩散方程 [9] [10] 。和上面提到的传统方法相比,这种方法不需要原始KdV方程的显式解的表达式。几何奇异摄动方法对给出扰动解的第一个图形起着非常特殊的作用,它发展了一种非常具有洞察力的思想,它可以在相对简单的极限形式附近构造非常复杂的动力学行为。一些著名的现象比如松弛振子,鸭解等都能通过几何奇异摄动方法来得到。
显然,具有时滞的扩散方程更加具有实际意义。 [11] [12] 分析了具有不同时滞的扩散方程的行波解。那么时滞KdV-KS方程是否具有孤立波解呢?这篇文章的目的就是建立具有分布时滞的KdV-KS方程
 (3)
(3)
的孤立波解的存在性。方程中 是时滞,
是时滞,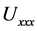 表示色散效应,
表示色散效应,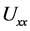 表示向后扩散,
表示向后扩散, 很小时也表示一个扰动。卷积
很小时也表示一个扰动。卷积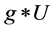 定义为
定义为
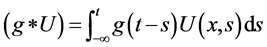
其中核函数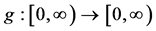 满足
满足 ,
, ;
; ,
, 。分布时滞的核函数
。分布时滞的核函数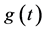 的平均时滞定义为
的平均时滞定义为 。这里,我们考虑
。这里,我们考虑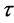 比较小的情况。
比较小的情况。
(3)的孤立波是一种特殊的行波解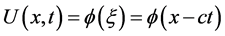 ,其中
,其中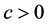 是速度,且
是速度,且 满足下面的泛函微分方程:
满足下面的泛函微分方程:
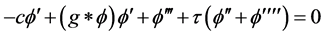 (4)
(4)
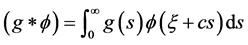 . (5)
. (5)
这里 表示对
表示对 求导,且
求导,且 。
。
选取不同的核函数,我们可以从(3)推导出不同类型的方程。常见的核函数形式有
 (6)
(6)
其中参数 表示时滞。第一种核起源于具有离散时滞的模型,其中
表示时滞。第一种核起源于具有离散时滞的模型,其中 表示狄拉克
表示狄拉克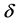 函数。另外两种分
函数。另外两种分
别称为弱和强时滞核。弱时滞 反应了过去的重要性呈指数递减。强时滞
反应了过去的重要性呈指数递减。强时滞 可认为是离散时滞的光滑版本。它暗示着过去的某个特定的时刻,即
可认为是离散时滞的光滑版本。它暗示着过去的某个特定的时刻,即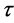 个单元之前,比其他时间更加重要,因为核函数在
个单元之前,比其他时间更加重要,因为核函数在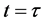 处取得唯一的最大值。这里,我们将考虑分布时滞核为弱核的情况。
处取得唯一的最大值。这里,我们将考虑分布时滞核为弱核的情况。
我们的主要思想是当平均时滞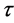 很小时,利用几何奇异摄动理论,将泛函微分方程(4)的存在性问题转化为二维不变流形中同宿轨的存在性问题。
很小时,利用几何奇异摄动理论,将泛函微分方程(4)的存在性问题转化为二维不变流形中同宿轨的存在性问题。
2. 预备知识
首先,我们给出证明孤立波存在性中需要用到的几何奇异摄动理论,它由Fenichel [7] 给出,为了方便起见,我们运用Jones [8] 的定理版本。
引理1:(几何奇异摄动理论)考虑系统:
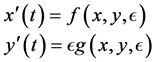 (7)
(7)
其中 ,
,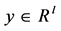 ,
, 是一个实参数,
是一个实参数, ,
, 是定义在
是定义在 上的
上的 函数,
函数,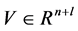 ,
, 是包含 的一个开区间。如果当
是包含 的一个开区间。如果当 时,系统包含一个紧的正规双曲的奇点流形
时,系统包含一个紧的正规双曲的奇点流形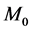 ,它包含在集合
,它包含在集合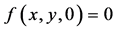 中,且图形由
中,且图形由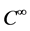 函数
函数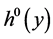 给出,其中
给出,其中 ,
, 是
是 中的一个紧区域,即
中的一个紧区域,即 ,那么对任意的
,那么对任意的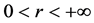 ,当
,当 且充分小时,存在一个流形
且充分小时,存在一个流形 :
:
(I) 位于 的
的 邻域内,且同胚于
邻域内,且同胚于 ;并且,它在(7)的流下是局部不变的且对
;并且,它在(7)的流下是局部不变的且对 是
是 的。
的。
(II) 对某个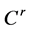 函数
函数 ,
, ,
,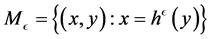 。
。
(III) 存在局部不变稳定和不稳定流形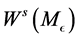 和
和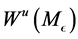 它们与
它们与 和
和 同胚且位于其
同胚且位于其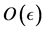 邻域中;并且,它在(7)的流下是局部不变的且对
邻域中;并且,它在(7)的流下是局部不变的且对 是
是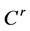 的。
的。
其次,我们给出非时滞情况下的对应结果。取 ,得非时滞方程:
,得非时滞方程:
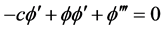 , (8)
, (8)
其中,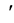 表示对
表示对 求导,利用在
求导,利用在 的边界条件,将方程(8)积分一次可化为:
的边界条件,将方程(8)积分一次可化为:
 .
.
进一步做变换 ,方程可变为:
,方程可变为:
 , (9)
, (9)
这里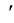 表示对
表示对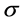 求导,它的等价形式为:
求导,它的等价形式为:
 (10)
(10)
引理2:在 的相平面中,方程(10)在
的相平面中,方程(10)在 的区域有一条趋于(0,0)的同宿轨。
的区域有一条趋于(0,0)的同宿轨。
证明:方程(10)有两个奇点(0,0),(2,0)。原点是鞍点,(2,0)是中心。很容易验证方程(10)是一个哈密
顿系统,哈密顿函数为: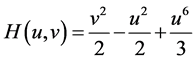 。考虑在区域
。考虑在区域 上的水平曲线
上的水平曲线 ,当
,当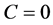 时,它包含趋于(0,0)的同宿轨,即
时,它包含趋于(0,0)的同宿轨,即 ,
,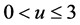 ,这正是KdV方程的一个孤立波,因此方程(10)存在一条同宿到(0,0)的同宿轨。
,这正是KdV方程的一个孤立波,因此方程(10)存在一条同宿到(0,0)的同宿轨。
3. 孤立波的存在性
这一节,我们将主要考虑时滞方程(3)的孤立波的存在性。运用行波形式,这个方程可以写为(4)~(5)。为了方便起见,我们分析下面的方程
 . (11)
. (11)
 . (12)
. (12)
其中 。如果我们能找到方程(11)的一个孤立波
。如果我们能找到方程(11)的一个孤立波 ,那么对应的
,那么对应的 就是方程(4)的孤立波,也即原方程(3)的孤立波解。
就是方程(4)的孤立波,也即原方程(3)的孤立波解。
下面,我们寻找正向孤立波,取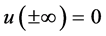 。特别地,我们考虑核函数是弱时滞
。特别地,我们考虑核函数是弱时滞 的情况,强时滞的情况非常相似,但是要复杂一点,这里我们略去。主要结果如下:
的情况,强时滞的情况非常相似,但是要复杂一点,这里我们略去。主要结果如下:
定理1 对任意充分小的 ,存在一个速度
,存在一个速度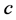 ,使得系统(11)有一个孤立波解。
,使得系统(11)有一个孤立波解。
证明:首先,我们把方程化为没有时滞的系统,定义
 ,
,
关于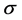 微分,我们得到
微分,我们得到
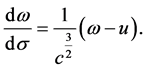
运用在 处的边界条件,将方程(11)积分一次可化为:
处的边界条件,将方程(11)积分一次可化为:
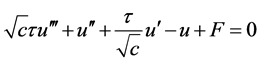 . (13)
. (13)
其中
 (14)
(14)
进一步,设 。则方程(13)~(14)可写为
。则方程(13)~(14)可写为
 (15)
(15)
从(15)~(14),我们得到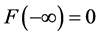 且
且
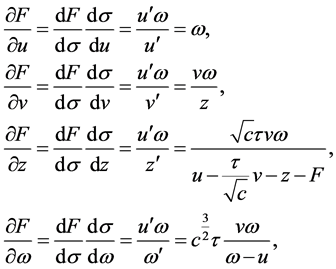
这暗示着 。
。
下面我们主要考虑系统(15),它与(11)等价。当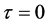 时,
时,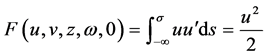 系统(15)简化为:
系统(15)简化为: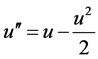 。这正是具有孤立波解的常微分方程(9)。
。这正是具有孤立波解的常微分方程(9)。
当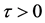 时,系统(15)定义了一个常微分方程组,其解在四维相平面
时,系统(15)定义了一个常微分方程组,其解在四维相平面 中,此时,该系统仍有奇点
中,此时,该系统仍有奇点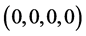 和
和 ,且在奇点
,且在奇点 的线性化矩阵为:
的线性化矩阵为:
 .
.
这个矩阵的特征值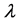 满足:
满足:
 . (16)
. (16)
考虑
 . (17)
. (17)
由Viete定理, 满足:
满足:
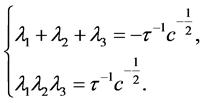
很容易得到,(17)有一个正实根 和两个负实根或具有复实部的共轭复根
和两个负实根或具有复实部的共轭复根 。显然,(16)有一个
。显然,(16)有一个
正的特征值 ,因此对所有的正数
,因此对所有的正数 和
和 ,奇点
,奇点 都有一个二维的稳定不变流形和一个
都有一个二维的稳定不变流形和一个
二维的不稳定不变流形。但是我们不能很明显的看出同宿轨。
下面,我们将用几何奇异摄动理论和中心流形定理证明,对充分小的 ,奇点
,奇点 有一条同宿轨。
有一条同宿轨。
做变换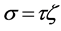 ,系统(15)化为
,系统(15)化为
 (18)
(18)
其中变量上的 表示对 的微分。一般来讲,系统(15)称为慢系统因为时间尺度
的微分。一般来讲,系统(15)称为慢系统因为时间尺度 是慢变量,而系统(18)称为快系统因为时间尺度
是慢变量,而系统(18)称为快系统因为时间尺度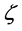 是快变量。这两个系统当
是快变量。这两个系统当 时是等价的。
时是等价的。
考虑慢系统(15),当 时,这个系统的流定义在集合
时,这个系统的流定义在集合

上,它是系统(15)的一个二维不变流形。如果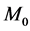 是正规双曲的,则对充分小的
是正规双曲的,则对充分小的 ,引理1 保证了我们能得到系统(15)的一个二维不变流形
,引理1 保证了我们能得到系统(15)的一个二维不变流形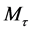 。在这个流形上研究系统(15),维数就简化为二维,同宿轨的存在性就能够得到。
。在这个流形上研究系统(15),维数就简化为二维,同宿轨的存在性就能够得到。
事实上,验证 在Fenichel [7] 的意义下是正规双曲的,只要验证快系统(18)的线性化矩阵限制在
在Fenichel [7] 的意义下是正规双曲的,只要验证快系统(18)的线性化矩阵限制在 上正好有
上正好有 个特征根在虚轴上,其余的谱都是双曲的。快系统(18)的线性化矩阵限制在
个特征根在虚轴上,其余的谱都是双曲的。快系统(18)的线性化矩阵限制在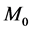 上可表示为:
上可表示为:
 .
.
它有四个特征值 ,因此,
,因此, 是正规双曲的。
是正规双曲的。
由几何奇异摄动理论,对充分小的 ,存在局部的二维不变流形
,存在局部的二维不变流形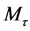 ,在系统(15)的流下,可以写成如下形式:
,在系统(15)的流下,可以写成如下形式:
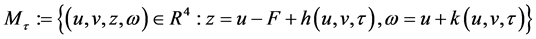 , (19)
, (19)
其中函数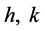 是定义在紧区域上的光滑函数,且满足:
是定义在紧区域上的光滑函数,且满足: ,
,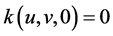 。将(19)代入慢系统(15),得
。将(19)代入慢系统(15),得 满足:
满足:
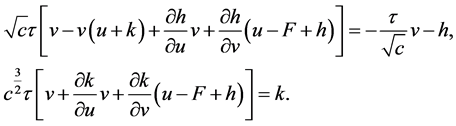 (20)
(20)
因为 很小,我们试图寻找这个偏微分方程关于
很小,我们试图寻找这个偏微分方程关于 的正则扰动级数解。又因为当
的正则扰动级数解。又因为当 时,
时,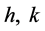 都等于0,所以可设
都等于0,所以可设 为
为
 (21)
(21)
将(21)代入(20)并对比 的同次幂的系数得:
的同次幂的系数得:

下面我们将研究系统(15)限制在 上的流,并证明它有一个孤立波。限制在
上的流,并证明它有一个孤立波。限制在 上的慢系统为
上的慢系统为
 (22)
(22)
很容易验证,当 时,系统(22)仍然有一个奇点
时,系统(22)仍然有一个奇点 。为了方便起见,我们把时滞参数和波速
。为了方便起见,我们把时滞参数和波速 作为变量,系统(22)等价于
作为变量,系统(22)等价于
 (23)
(23)
这时我们能在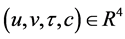 上研究流。我们寻找当
上研究流。我们寻找当 很小时系统(23)的同宿轨。由(23),奇点
很小时系统(23)的同宿轨。由(23),奇点 可看作一个由
可看作一个由 参数化的奇点曲面
参数化的奇点曲面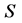 ,即
,即 。反过来,这个奇点的不稳定流形
。反过来,这个奇点的不稳定流形 和稳定流形
和稳定流形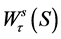 交于
交于 的曲线上。即引理2 中的同宿轨。进一步,由引理1,
的曲线上。即引理2 中的同宿轨。进一步,由引理1,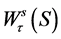 和
和 一定仍交于超平面
一定仍交于超平面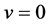 上。在集合
上。在集合 上,我们分别参数化
上,我们分别参数化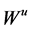 和
和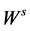 为
为 和
和 ,并定义:
,并定义:
 (24)
(24)
则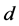 的零点就能产生同宿轨。由引理1,当
的零点就能产生同宿轨。由引理1,当 时存在与
时存在与 无关的同宿轨,于是我们有
无关的同宿轨,于是我们有 ,设
,设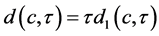 ,则
,则
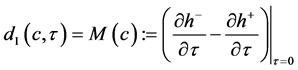 . (25)
. (25)
下面我们给出一个引理:
引理3 对任意充分小的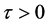 ,存在速度
,存在速度 ,使得(25)中定义的
,使得(25)中定义的 满足:
满足:
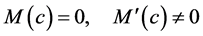 (26)
(26)
证明:我们用微分形式来量化这些信息。(23)的变分方程在 时的微分形式为:
时的微分形式为:
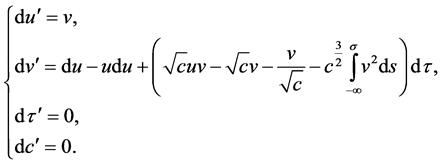
对不变流形 和
和 的切空间
的切空间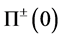 ,在
,在 (此时
(此时 )处很容易找到切于
)处很容易找到切于 和
和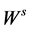 的三个切向量:
的三个切向量:

其中 中的
中的 满足
满足 ,即
,即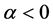 ,通过计算
,通过计算

其中 是(1,2,3)的排列。进一步,
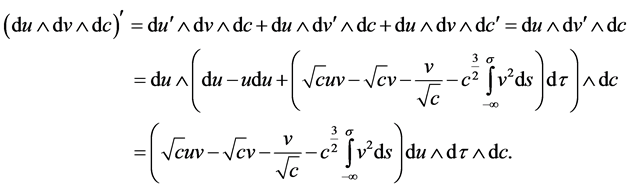
类似的,运用到在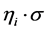 ,
,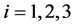 处的切空间
处的切空间 上,形式
上,形式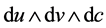 也能够具体计算出来。因为
也能够具体计算出来。因为

所以 。于是
。于是
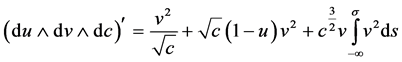 .
.
设 ,我们得到
,我们得到
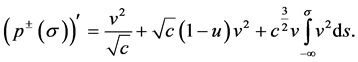
很容易验证:当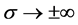 时,
时, 。且
。且
 .
.
这就证明了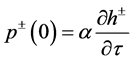 ,即
,即

因此,我们有
 .
.
所以,

于是,存在唯一的值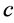 ,使得
,使得 。引理得证。
。引理得证。
由引理3:和隐函数定理,对充分小的 ,
, 在
在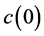 附近有唯一的根
附近有唯一的根 ,因此,
,因此, 也有唯一的根
也有唯一的根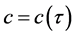 。定理得证。
。定理得证。
致谢
感谢评审专家对论文提出的宝贵意见;感谢国家留学基金的资助。
文章引用
蒋永新, (2014) 具有分布时滞的奇异扰动KdV-KS方程的孤立波
Solitary Waves of Singularly Perturbed KdV-KS Equation with Distributed Delay. 理论数学,06,251-260. doi: 10.12677/PM.2014.46037
参考文献 (References)
- 1. Korteweg, D.J. and de Vries, G. (1895) On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philosophical Magazine, 39, 422-443.
- 2. Gu, C.H. and Hu, H.S. (2005) Darboux transformation in integrable systems. Springer-Verlag, Berlin.
- 3. Olver, P.J. (1986) Applications of lie groups to differential equations. Grad. Texts in Math., Springer-Verlag, Berlin.
- 4. Ercolani, N.M., McLaughlin, D.W. and Roitner, H. (1993) Attractors and transients for a perturbed periodic KDV equation: A nonlinear spectral analysis. Journal of Nonlinear Science, 3, 477-539.
- 5. Ogawa, T. (1994) Travelling wave solutions to perturbed Korteweg-de Vries equations. Hiroshima Mathematica Journal, 24, 401-422.
- 6. Fan, X. and Tian, L. (2005) The existence of so-litary waves of singularly perturbed mKdV-KS equation. Chaos, Solitons Fractals, 26, 1111-1118.
- 7. Fenichel, N. (1979) Geometric singular perturbation theory for ordinary differential equations. Journal of Differential Equations, 31, 53-98.
- 8. Jones, C.K.R.T. (1995) Geometrical singular perturbation theory. In: Johnson, R., Ed., Dynamical Systems, Lecture Notes in Mathematics Vol. 1609, Springer, New York, 44-118.
- 9. Ruan, R. and Xiao, D. (2004) Stability of steady states and existence of travelling waves in a vector-disease model. Proceedings Royal Society of Edinburgh, 134A, 991-1011.
- 10. Mansour, M.B.A. (2013) A geometric construction of traveling waves in a generalized nonlinear dispersive-dissipative equation. Journal Geometry and Physics, 69, 116-122.
- 11. Ashwin, P., Bartucclli, M.V., Bridges, T.J. and Gourley, S.A. (2002) Travelling fronts for the KPP-Fisher equation with spatiotemporal delay. Zeit-schriftfürangewandte Mathematik und Physik, 53, 103-122.
- 12. Zhao, Z.H. (2008) Solitary waves of the generalized KdV equation with distributed delays. Journal of Mathematical Analysis and Applications, 344, 32-41.