Pure Mathematics
Vol.06 No.06(2016), Article ID:19053,10
pages
10.12677/PM.2016.66067
A Normality Criterion Concerning the Zeros’ Multiplicity of 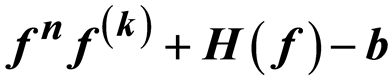
Jing Li1, Jun’an Zhao2, Bingmao Deng1
1Institute of Applied Mathematics, South China Agricultural University, Guangzhou Guangdong
2Department of Mathematics, Jinan University, Guangzhou Guangdong
Received: Nov. 5th, 2016; accepted: Nov. 20th, 2016; published: Nov. 28th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we study the normality of holomorphic functions and prove the following results: Let  be three positive integers satisfying
be three positive integers satisfying 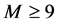 when
when  and
and 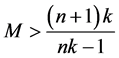 when
when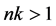 ,
, 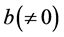 is a finite complex number; let
is a finite complex number; let 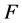 be a family of holomorphic functions in a domain
be a family of holomorphic functions in a domain 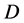 and
and 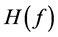 be a differential polynomial of
be a differential polynomial of 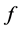 and satisfy
and satisfy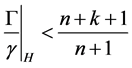 , if for each
, if for each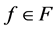 , satisfies (1) all zeros of
, satisfies (1) all zeros of 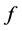 have multiplicity at least
have multiplicity at least ; (2) all zeros of
; (2) all zeros of 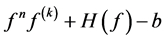 have multiplicity
have multiplicity , then
, then  is normal in
is normal in .
.
Keywords:Meromorphic Function, Normal Family, Zalcman Lemma, Differential Polynomial

涉及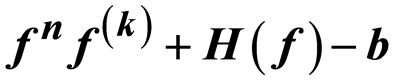 的零点重级的正规定则
的零点重级的正规定则
李菁1,赵隽安2,邓炳茂1
1华南农业大学数学研究所,广东 广州
2暨南大学数学系,广东 广州

收稿日期:2016年11月5日;录用日期:2016年11月20日;发布日期:2016年11月28日

摘 要
本文研究全纯函数族的正规性,证明了如下结论:设 为三个正整数,其中当
为三个正整数,其中当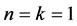 时,
时,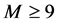 ;当
;当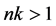 时,
时, ,
, 为一个非零有穷复数,设
为一个非零有穷复数,设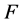 为区域
为区域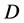 内的一族全纯函数,
内的一族全纯函数, 为
为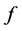 的微分多项式且满足
的微分多项式且满足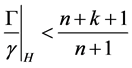 ,若对于
,若对于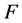 中的每一个函数
中的每一个函数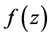 均有(1)
均有(1)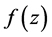 的零点重级
的零点重级 ;(2)
;(2)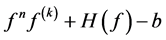 的零点重级
的零点重级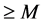 ,则
,则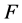 在
在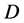 内正规。
内正规。
关键词 :亚纯函数,正规族,Zalcman引理,微分多项式

1. 引言及主要结果
本文采用Nevanlinna理论中的记号 [1] [2] ,如 ,
,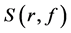 ,
, ,
, ,
,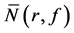 ,
,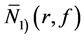 ,
,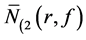 等,其中
等,其中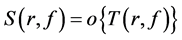 (除去一个有穷测度集),
(除去一个有穷测度集),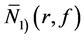 表示
表示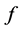 的极点重数
的极点重数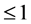 的密指量,
的密指量,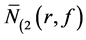 表示
表示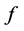 的极点重数
的极点重数 的不计重数的密指量。
的不计重数的密指量。
设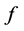 为区域
为区域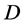 内的亚纯函数,
内的亚纯函数,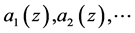 均在
均在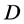 内全纯,
内全纯,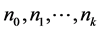 是非负整数,则称
是非负整数,则称 为
为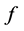 的微分单项式,
的微分单项式, 和
和 分别称为
分别称为 的次数和权。设
的次数和权。设 均为
均为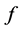 的微分单项式,则称
的微分单项式,则称 为
为 的微分多项式,
的微分多项式, 与
与 分别称为
分别称为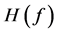 的次数和权,
的次数和权,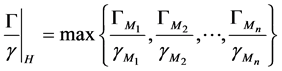 称为
称为 的权与次数的比。
的权与次数的比。
设 是复平面
是复平面 上的一个区域,
上的一个区域, 是
是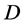 内的一族亚纯函数。
内的一族亚纯函数。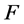 在
在 内正规是指从
内正规是指从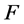 中任取一个函数序列
中任取一个函数序列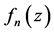 ,必存在一个子序列
,必存在一个子序列 在
在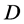 内按球面距离内闭一致收敛到一个亚纯函数或
内按球面距离内闭一致收敛到一个亚纯函数或 。另外,设
。另外,设 是
是 内的一点,如果存在
内的一点,如果存在 的一个邻域
的一个邻域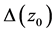 使得
使得 在
在 内正规,则称
内正规,则称 在
在 处正规。
处正规。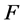 在
在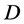 内正规当且仅当
内正规当且仅当 在
在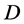 内的每一点都正规。
内的每一点都正规。
在亚纯函数正规族理论中,寻找新的正规定则是一个重要问题。
1965年,杨乐和张广厚 [3] 证明了
定理A [3] :设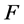 为区域
为区域 内的一族全纯函数,
内的一族全纯函数, 为一个正整数,
为一个正整数, 为一个非零有穷复数。如果对于
为一个非零有穷复数。如果对于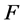 中的每一个函数
中的每一个函数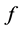 均有
均有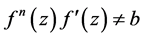 ,则
,则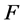 在
在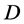 内正规。
内正规。
1982年,Oshkin [4] 进一步证明了
定理B [4] :设 为区域
为区域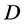 内的一族全纯函数,
内的一族全纯函数, 为一个非零有穷复数。如果对于
为一个非零有穷复数。如果对于 中的每一个函数
中的每一个函数 均有
均有 ,则
,则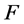 在
在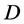 内正规。
内正规。
1993年,方明亮和徐万松 [5] 推广了上述定理,把 换成了
换成了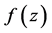 的线性微分多项式
的线性微分多项式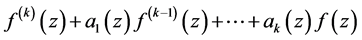 ,证明了
,证明了
定理C [5] :设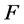 为区域
为区域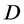 内的一族全纯函数,
内的一族全纯函数,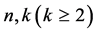 为两个正整数,
为两个正整数, 为一个非零有穷复数,
为一个非零有穷复数, 均在
均在 内全纯,若对于
内全纯,若对于 中的每一个函数
中的每一个函数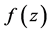 均有:(1)
均有:(1) 的零点重级
的零点重级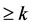 ;(2)
;(2)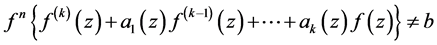 ,则
,则 在
在 内正规。
内正规。
定理D [5] :设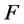 为区域
为区域 内的一族全纯函数,
内的一族全纯函数,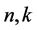 为两个正整数,
为两个正整数,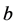 为一个非零有穷复数,若对于
为一个非零有穷复数,若对于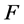 中的每一个函数
中的每一个函数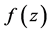 均有:(1)
均有:(1)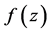 的零点重级
的零点重级 ;(2)
;(2)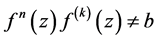 ,则
,则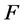 在
在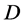 内正规。
内正规。
本文进一步证明了
定理1:设 为三个正整数,其中当
为三个正整数,其中当 时,
时,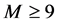 ;当
;当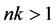 时,
时, ,
, 为一个非零有穷复数,设
为一个非零有穷复数,设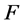 为区域
为区域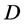 内的一族全纯函数,
内的一族全纯函数, 为
为 微分多项式且满足
微分多项式且满足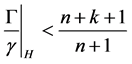 ,若对于
,若对于 中的每一个函数
中的每一个函数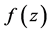 均有:(1)
均有:(1)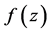 的零点重级
的零点重级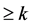 ;(2)
;(2) 的零点重级
的零点重级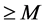 ,则
,则 在
在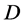 内正规。
内正规。
推论2:设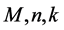 为三个正整数,其中当
为三个正整数,其中当 时,
时, ;当
;当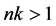 时,
时,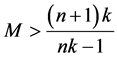 ,
, 为一个非零有穷复数,设
为一个非零有穷复数,设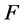 为区域
为区域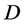 内的一族全纯函数,若对于
内的一族全纯函数,若对于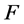 中的每一个函数
中的每一个函数 均有:(1)
均有:(1) 的零点重级
的零点重级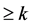 ;(2)
;(2)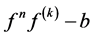 的零点重级
的零点重级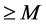 ,则
,则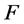 在
在 内正规。
内正规。
2. 几个引理
引理1 [6] :设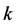 为一个正整数,
为一个正整数,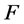 为单位圆
为单位圆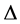 内的一族亚纯函数,且
内的一族亚纯函数,且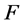 中的每个函数的零点的重级至少是
中的每个函数的零点的重级至少是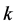 ,则对于任意实数
,则对于任意实数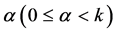 ,
,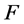 在
在 处不正规的充要条件是,存在
处不正规的充要条件是,存在
a) 实数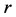 ,
,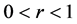 ;
;
b) 点列 ,
,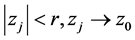 ;
;
c) 正数列 ;
;
d) 函数列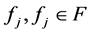 ,
,
使得函数列 在
在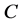 内按球面距离内闭一致收敛于一个非常数亚纯函数
内按球面距离内闭一致收敛于一个非常数亚纯函数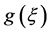 ,且
,且 的零点重级至少是
的零点重级至少是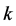 。
。
引理2:设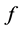 为一个非常数整函数,
为一个非常数整函数, 为一个非零有穷复数,则有
为一个非零有穷复数,则有
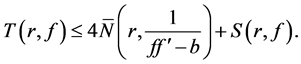 (1)
(1)
证明:不妨设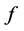 不是一个线性多项式。令
不是一个线性多项式。令
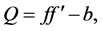 (2)
(2)
则
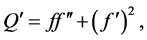 (3)
(3)
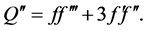 (4)
(4)
由(2) (3)得, 。于是有,
。于是有,
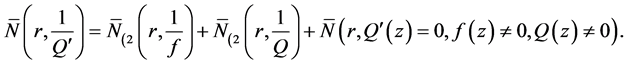 (5)
(5)
令 ,则有
,则有
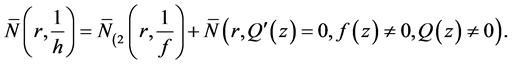 (6)
(6)
根据Nevanlinna第一基本定理得
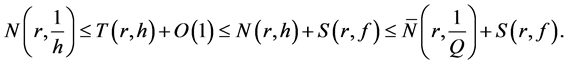 (7)
(7)
设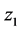 是
是 的一个重零点,那么
的一个重零点,那么 是
是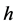 的重零点,则
的重零点,则 ,于是由(6),(7)得
,于是由(6),(7)得
 (8)
(8)
由(2) (3)可得
 (9)
(9)
其中
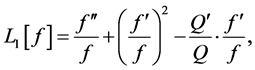 (10)
(10)
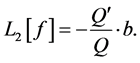 (11)
(11)
显然 ,且
,且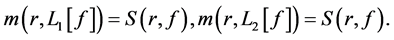
由Nevanlinna第一基本定理以及(9) (10)和(11)得
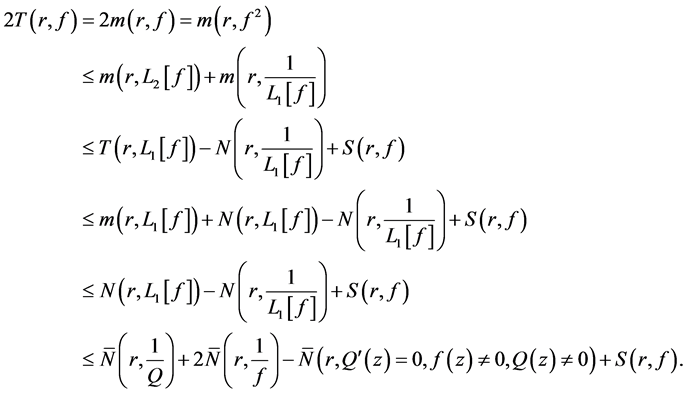 (12)
(12)
令
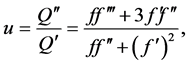 (13)
(13)
由于 不是一个线性多项式,故
不是一个线性多项式,故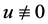 。由(13)得
。由(13)得
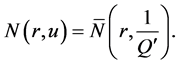 (14)
(14)
令
 (15)
(15)
由(13) (15)得, 的极点来自
的极点来自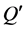 的零点,则有
的零点,则有
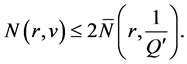 (16)
(16)
令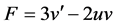 ,且
,且
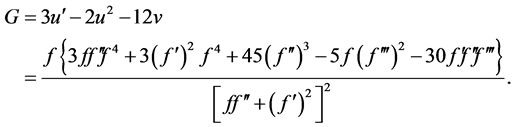 (17)
(17)
我们断言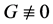 。
。
事实上,假设 。由(13)得
。由(13)得
 (18)
(18)
由(15) (18)得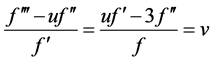 。于是有
。于是有
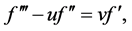 (19)
(19)
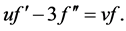 (20)
(20)
对(20)式求导得
 (21)
(21)
结合(19) (21)得
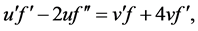 (22)
(22)
进一步结合(20) (22)得到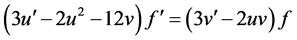 ,即
,即
 (23)
(23)
因为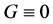 ,由(23)得,
,由(23)得,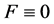 。即
。即
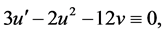 (24)
(24)
 (25)
(25)
对(24)式求导得
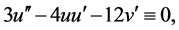 (26)
(26)
结合(25) (26)得
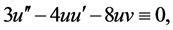 (27)
(27)
进一步结合(24) (27)得
 (28)
(28)
由于 没有极点,故
没有极点,故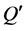 也没有极点。由(13)式知,
也没有极点。由(13)式知, 要么是整函数,要么是只含简单极点且在极点处的留数为正整数的亚纯函数。以下分两种情形讨论。
要么是整函数,要么是只含简单极点且在极点处的留数为正整数的亚纯函数。以下分两种情形讨论。
情形1: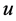 是整函数。
是整函数。
由(28)得, 不可能是多项式,则
不可能是多项式,则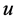 只能是超越整函数。于是有
只能是超越整函数。于是有
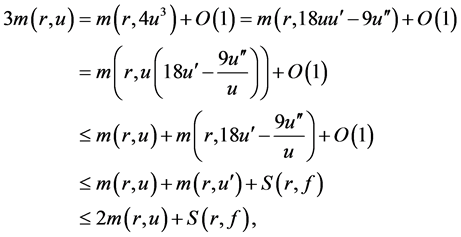
故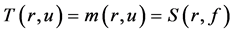 ,这与
,这与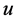 是超越整函数矛盾。
是超越整函数矛盾。
情形2: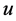 是只含简单极点且在极点处的留数为正整数的亚纯函数。
是只含简单极点且在极点处的留数为正整数的亚纯函数。
设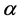 是
是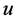 的简单极点,且
的简单极点,且 在
在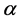 处的留数是
处的留数是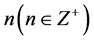 ,则有
,则有

故(28)式左边可写成

显然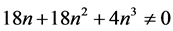 ,故(28)式不可能成立,矛盾。因此
,故(28)式不可能成立,矛盾。因此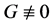 。
。
由(17)得,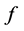 的单零点必为
的单零点必为 的零点,又因为
的零点,又因为 ,结合(14) (16),则有
,结合(14) (16),则有
 (29)
(29)
由于
 (30)
(30)
综合(5) (8) (12) (29)和(30)得
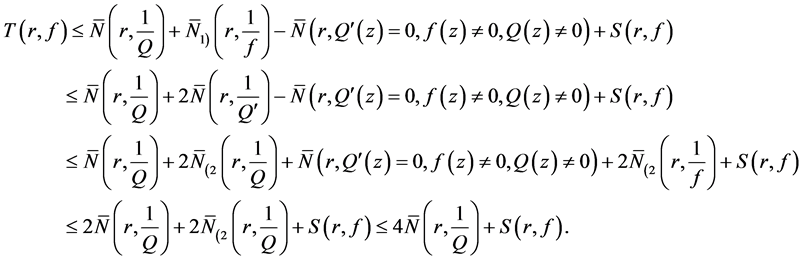
于是引理2得证。
注:引理2的证明方法参考了文献 [7] [8] 。
引理3:设 为三个正整数,其中当
为三个正整数,其中当 时,
时,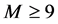 ;当
;当 时,
时,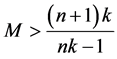 ,
, 为一个非零有穷复数,设
为一个非零有穷复数,设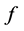 是一个整函数,若
是一个整函数,若 满足:(1)
满足:(1) 的零点重级均
的零点重级均 ;(2)
;(2)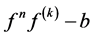 的零点重级均
的零点重级均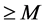 ,则
,则 恒为常数。
恒为常数。
证明:假设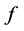 不恒为常数. 以下分两种情况讨论。
不恒为常数. 以下分两种情况讨论。
情形1: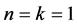 。
。
根据引理2及Nevanlinna第一基本定理得

即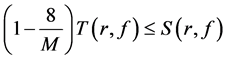 ,即
,即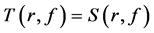 。矛盾。
。矛盾。
情形2: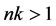 。
。
若 ,则
,则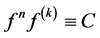 (
( 为一个常数)。如果
为一个常数)。如果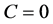 ,则
,则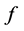 为次数
为次数 的多项式,又因为
的多项式,又因为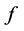 的零点重级
的零点重级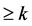 ,则
,则 恒为常数,矛盾;如果
恒为常数,矛盾;如果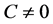 ,显然
,显然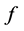 没有零点也没有极点,且
没有零点也没有极点,且 ,由Nevanlinna第一基本定理得
,由Nevanlinna第一基本定理得
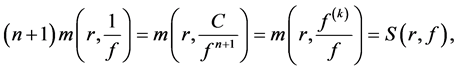
进而 即
即 ,则
,则 恒为常数,矛盾。因此
恒为常数,矛盾。因此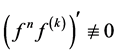 。
。
根据Nevanlinna第一基本定理得

上式两边同时加上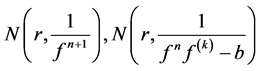 ,得
,得

于是有

由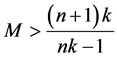 得,
得,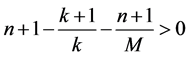 ,故
,故 ,矛盾。
,矛盾。
于是引理3得证。
3. 定理1的证明
不妨设区域 为单位圆
为单位圆 。假设定理1不真,则必存在
。假设定理1不真,则必存在 内一点
内一点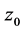 ,使得
,使得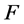 在
在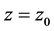 处不正规。因而由引理1知,存在
处不正规。因而由引理1知,存在
a) 实数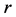 ,
,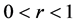 ;
;
b) 点列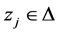 ,
,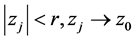 ;
;
c) 正数列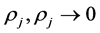 ;
;
d) 函数列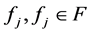 ,
,
使得函数列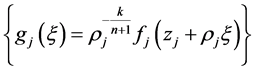 在复平面上的任意紧子集上一致收敛到一个非常数整函数
在复平面上的任意紧子集上一致收敛到一个非常数整函数 ,且
,且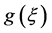 的零点重级均
的零点重级均 。因为
。因为
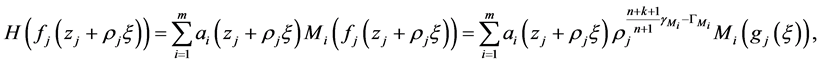
所以
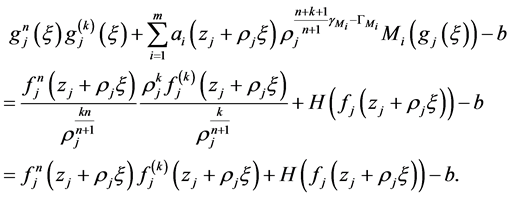
由于 在
在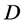 内全纯,
内全纯,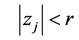 ,
, ,故在
,故在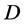 内任意紧子集上当
内任意紧子集上当 充分大时一致有
充分大时一致有
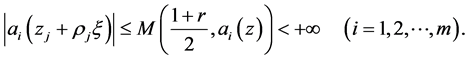
又因为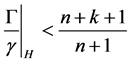 ,所以
,所以 。故函数
。故函数
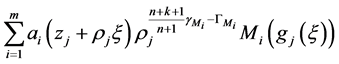 在
在 内任意紧子集上一致收敛于零。故
内任意紧子集上一致收敛于零。故
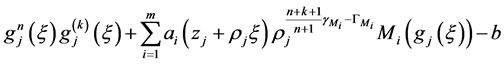
在 内任意紧子集上一致趋于
内任意紧子集上一致趋于
于是有,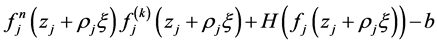 在
在 内任意紧子集上一致收敛到
内任意紧子集上一致收敛到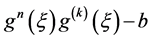 。由Hurwitz定理知,
。由Hurwitz定理知, 的零点重级均
的零点重级均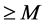 ,则根据引理3得
,则根据引理3得 恒为常数,矛盾。于是
恒为常数,矛盾。于是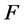 在
在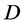 内正规。定理1证毕。
内正规。定理1证毕。
4. 推论2的证明
推论2的证明方法与定理1的证明方法完全一样,故在此省略。
致谢
作者由衷地感谢方明亮教授的悉心指导!
基金项目
国家自然科学基金(No.11371149)资助。
文章引用
李 菁,赵隽安,邓炳茂. 涉及fnf(k)+H(f)-b 的零点重级的正规定则
A Normality Criterion Concerning the Zeros’ Multiplicity of fnf(k)+H(f)-b[J]. 理论数学, 2016, 06(06): 486-495. http://dx.doi.org/10.12677/PM.2016.66067
参考文献 (References)
- 1. Hayman, W.K. (1964) Meromorphic Function. Clarendon Press, Oxford.
- 2. Yang, L. (1993) Value Distribution theory. Sprin-ger-Verlag & Science Press, Berlin.
- 3. Yang, L. and Zhang, G.H. (1965) Recherchessur la normalit des familles de fonctionsanalytiquesa des valeurs multiples. Un nouveau crit re etquelques applications. Sci. Sinica, 14, 1258-1271.
- 4. Oshkin, I. (1982) A Normal Criterion of Families of Holomorphic Functions. Usp. Mat. Nauk, 37, 221-222. (In Russian)
- 5. 方明亮, 徐万松. 关于Oshkin的一个定理[J]. 南京航空航天大学学报, 1993(25): 714-718.
- 6. 方明亮. 一族亚纯函数的正规定则[J]. 数学学报, 1994: 86-90.
- 7. 仪洪勋. 关于 的值分布[J]. 科学通报, 1989(10): 727-730.
- 8. Clunie, J. (1967) On a result of Hayman. Journal of the London Mathematical Society, 42, 389-392. https://doi.org/10.1112/jlms/s1-42.1.389