Pure Mathematics
Vol.07 No.02(2017), Article ID:20059,10
pages
10.12677/PM.2017.72013
Parallel Methods for Parabolic Equations Based on MPI Implementation
Yuyang Gao, Haiming Gu
Qingdao University of Science and Technology, Qingdao Shandong

Received: Mar. 11th, 2017; accepted: Mar. 28th, 2017; published: Mar. 31st, 2017

ABSTRACT
Many applications in mathematics and engineering involve numerical solutions of partial differential equations (PDEs). The demands of large-scale computing are quickly increasing in modern science and technology, and parallel computing has received more and more attention. In this paper, the main idea is that classical Group Explicit method (GEM) for parabolic equations, the group explicit method is established briefly and the stability analysis of the method is indicated simply. Then we focus on how to calculate the format in MPI parallel environment. Two parallel MPI algorithms are established and compared with non-parallel algorithm based on GEM. They are MPI block communication (wait communication) and non-blocking communication (no-wait communication). These two MPI schemas both better than one single process to calculate numerical solutions use group explicit method. Also, the non-blocking communication program has higher computational efficiency than blocking communication program.
Keywords:Finite Difference Method, Group Explicit Method, Parabolic Equations, MPI (Message Passing Interface)
求解抛物方程的MPI并行方法
高玉羊,顾海明
青岛科技大学,山东 青岛
收稿日期:2017年3月11日;录用日期:2017年3月28日;发布日期:2017年3月31日

摘 要
数值求解偏微分方程广泛应用于数学与工程领域。大规模数值计算在当今科学技术运用中得到飞速发展,其中可并行的有限差分格式受到越来越多的重视。在本文中,主要阐述了经典的分组显示方法求解抛物方程,并简单扼要的分析了该格式的建立以及稳定性。随后本文着重介绍了如何在MPI并行环境下对该格式进行数值计算,构建了两种不同的并行计算模型,即阻塞通信(等待模式)和非阻塞通信(即非等待模式)模式。并与非并行状态下的差分格式做出比较,结果表明,相对于一个进程求解偏微分方程,两种模式都表现出较好的效果,而且非阻塞通信相较于阻塞通信模式亦表现出较好的并行效率。
关键词 :有限差分法,分组显式格式,抛物方程,MPI (Message Passing Interface)

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
现代科学技术的发展很大程度上依赖于物理学、化学、生物学的成就与进展,而这些学科自身的精确化又是他们取得进展的重要保证。学科的精确化往往是通过建立数学模型来实现的,而数学模型的大都可以归纳为偏微分方程的形式。现代科学技术对大规模科学与工程计算的需求日益增长,在科学与工程计算领域提出了许多大规模计算和超大规模计算问题,解决这些问题需要在高性能并行计算机( [1] [2] )上进行,而并行计算机系统的研制和发展推动了偏微分方程并行算法的研究与发展。
分组显式方法(文献 [3] )是Evans等人上世纪80年代设计的可以并行计算的经典有限差分算法。分组显式格式是使用不同类型的Saul'yev非对称格式( [4] )进行恰当的组合,在不同的时间层上连续交替的使用不同的非对称格式,这样,可带来截断误差的明显改善,从而使算法的精度得以提高。基于分组显式的思想,有限并行差分格式得到广泛的发展并应用于求解其他偏微分方程( [5] [6] [7] )中。
MPI是目前最重要的并行编程工具( [8] ),它具有移植性好、功能强大、效率高等多种优点,MPI其实是一个“库”,共有上百个函数调用接口,在FORTRAN和C语言中可以直接对这些函数进行调用。MPI为并行算法提供了多种通信模式,一般的阻塞通讯模式即可满足大多数并行算法,但非阻塞通讯模式由于相对减少了通讯时间,从而使并行模式的效率得到较好的提升。将MPI并行技术与有限并行差分格式结合需要构造相匹配的消息传递模型( [9] ),因此,构造合适的并行消息传递模型是并行数值计算偏微分方程的重点。
2. 有限并行差分格式
2.1. 分组显式方法
在区域 上,考虑如下附有初始条件和边界条件的抛物方程。
上,考虑如下附有初始条件和边界条件的抛物方程。
 (1)
(1)
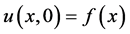 (2)
(2)
 (3)
(3)
将区域 进行剖分,空间步长
进行剖分,空间步长 ,
, 为正整数,时间步长为
为正整数,时间步长为 ,
, ,
, 。为简单计,将节点
。为简单计,将节点 记为
记为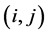 。构造分组显式格式需要用到Saul’yev非对称格式。首先,可以得到以下很明显的关系式,
。构造分组显式格式需要用到Saul’yev非对称格式。首先,可以得到以下很明显的关系式,
 (4)
(4)
 (5)
(5)
应用如下等式
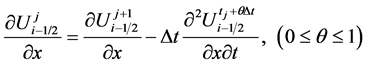
将(4),(5)代入方程(1)得到
 (7)
(7)
最后,应用如下显然的表达式
 (8)
(8)
 (9)
(9)
便可以将(7)写成如下形式,
 (10)
(10)
其中,
 (11)
(11)
令 ,并舍弃无穷小项
,并舍弃无穷小项 ,可以得到如下网格方程,
,可以得到如下网格方程,
 (12)
(12)
完全类似的可以推导出公式
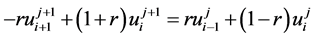 (13)
(13)
将方程(12)、(13)写成矩阵的形式,
 (14)
(14)
将矩阵移向右侧,(14)可以写成
 (15)
(15)
其中 ,因此方程(15)可以写成如下矩阵的形式,
,因此方程(15)可以写成如下矩阵的形式,
 (16)
(16)
在靠近求解区域左边界和右边界的点可以分别使用方程(12)、(13)进行求解。
 (17)
(17)
 (18)
(18)
以上即为分组显式格式的基本思想,为了适配下文中的MPI消息传递模型,将会选择适当的内部节点数进行网格剖分。考虑区域 上的划分间隔为偶数,既
上的划分间隔为偶数,既 为偶数,则在每一时间层上,内部节点数为
为偶数,则在每一时间层上,内部节点数为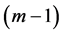 ,为奇数。这样,就会存在一个单独的点无法使用方程(14)求解。为了更好的处理边界节点的值,在下文中给出了具体的方法。
,为奇数。这样,就会存在一个单独的点无法使用方程(14)求解。为了更好的处理边界节点的值,在下文中给出了具体的方法。
2.2. 交替分组方法
在每一时间层,除初始条件外,所有内部节点是未知的。内部节点的最后一个点使用格式(18),其余
诸点,从内部节点的第一个点开始到第 个内部节点使用方程(16),共进行
个内部节点使用方程(16),共进行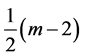 次计算,将该
次计算,将该
格式称为右端分组显式(GER)格式。写成矩阵的形式如下,
 (19)
(19)
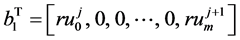
方程(19)写成矩阵的形式为
 (20)
(20)
其中




运用相似的方法,在每一时间层,内部节点的第一个节点使用方程(18),其余内部节点使用方程(16),可以得到左端分组显式(GEL)格式。
 (21)
(21)

在相邻的时间层上交替使用方程(20)、(21),即可得到交替分组方法(AGE)。其矩阵形式如下,
 (22)
(22)
方程(16)的稳定分析在文献 [3] 中已经得到充分的说明,稳定性条件为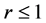 时误差的增长得到有效的控制,同样,使用文献 [10] 中的Kellogg引理,可以得到方程(20),(21),(22)的稳定性条件为
时误差的增长得到有效的控制,同样,使用文献 [10] 中的Kellogg引理,可以得到方程(20),(21),(22)的稳定性条件为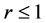 。
。
3. MPI并行算法
在本文中,所有并行算法都是针对上文中给出的有限差分格式进行并行化计算。将求解区域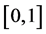 划分为若干大致相等的区域,比如说,若将方程(1)进行4进程并行计算,就将求解区域化为4条带状的区域,每个进程负责一条带状计算区域,在时间层上逐次计算,为了实现高效计算,比较适宜的做法是为每一条进程分配大约相等的任务量,即保证在空间方向上分割的带状区域大小几乎是一致的。每个相邻进程进行数据通信,当通信与计算完毕,继续进行下一时间层的计算。下文中,将会给出两种不同的通讯模式,即阻塞通信与非阻塞通信,对交替分组格式进行并行计算。表1和表2分别展示了MPI阻塞通信与非阻塞通信的步骤流。
划分为若干大致相等的区域,比如说,若将方程(1)进行4进程并行计算,就将求解区域化为4条带状的区域,每个进程负责一条带状计算区域,在时间层上逐次计算,为了实现高效计算,比较适宜的做法是为每一条进程分配大约相等的任务量,即保证在空间方向上分割的带状区域大小几乎是一致的。每个相邻进程进行数据通信,当通信与计算完毕,继续进行下一时间层的计算。下文中,将会给出两种不同的通讯模式,即阻塞通信与非阻塞通信,对交替分组格式进行并行计算。表1和表2分别展示了MPI阻塞通信与非阻塞通信的步骤流。
考虑划分区域内部间隔为偶数 ,内部节点数
,内部节点数 (同上文,划分区域第一个节点标号为0,最后一个节点标号为
(同上文,划分区域第一个节点标号为0,最后一个节点标号为 ),内点数为奇数。不失一般性,考虑以上差分格式在4条进程下完成并行计算,不妨假设已知时间层为
),内点数为奇数。不失一般性,考虑以上差分格式在4条进程下完成并行计算,不妨假设已知时间层为 上的数据,计算时间层为
上的数据,计算时间层为 上的值时,将内部节点大约的分为4个部分,由于节点
上的值时,将内部节点大约的分为4个部分,由于节点
Table 1. The steps of blocking communication mode
表1. 阻塞通信模式下并行详细步骤
Table 2. The steps of non-blocking communication mode
表2. 非阻塞通信模式下并行详细步骤
数是 为奇数,则必然有一个点无法使用方程(16)分组计算。在使用GEL格式计算的情况下,在0号进程中,划分区域内部节点的第1个点由方程(17)计算,进程0的其他节点和其他进程的点使用方程(16)计算。由于与0号进程相邻的1号进程之间需要进行数据通信,既计算第
为奇数,则必然有一个点无法使用方程(16)分组计算。在使用GEL格式计算的情况下,在0号进程中,划分区域内部节点的第1个点由方程(17)计算,进程0的其他节点和其他进程的点使用方程(16)计算。由于与0号进程相邻的1号进程之间需要进行数据通信,既计算第 层中0号进程的最右端的两个点需要第
层中0号进程的最右端的两个点需要第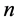 层中的1号进程的第一个点的数据,计算第
层中的1号进程的第一个点的数据,计算第 层中1号进程最左端两个点需要第
层中1号进程最左端两个点需要第 层中0号进程最右端一个点的数据,其他进程如1号进程与2号进程、2号进程与3号进程之间的通讯也是如此。在下文中,以0,1号进程之间的通讯传递为例,给出MPI通信模型,GEL通讯简图见图1。
层中0号进程最右端一个点的数据,其他进程如1号进程与2号进程、2号进程与3号进程之间的通讯也是如此。在下文中,以0,1号进程之间的通讯传递为例,给出MPI通信模型,GEL通讯简图见图1。
在使用GER格式计算的情况下,与GEL格式类似,单独的内部节点的计算由最后一个进程执行,既 时间层中3号进程的最右端内部节点由方程(18)计算,其他节点两两成组由方程(16)计算,与GEL格式一致,相邻进程的节点进行数据通信,GER通讯简图见图2。
时间层中3号进程的最右端内部节点由方程(18)计算,其他节点两两成组由方程(16)计算,与GEL格式一致,相邻进程的节点进行数据通信,GER通讯简图见图2。
在使用交替分组格式计算的情况下,与GER,GEL格式有些不同之处,首先考虑在第 层上使用GEL格式,在第
层上使用GEL格式,在第 层上使用GER格式,第
层上使用GER格式,第 层上的通讯与计算与普通的GEL格式一样,在进行
层上的通讯与计算与普通的GEL格式一样,在进行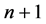 层上的计算时,相邻两个进程的最后两个数据与最初的两个数据分别向后一个进程和前一个进程发送。通讯简图如图3。
层上的计算时,相邻两个进程的最后两个数据与最初的两个数据分别向后一个进程和前一个进程发送。通讯简图如图3。
在MPI并行环境下,阻塞通信模式下用到的计算与通讯过程中的命令,如下,
MPI_Send(void* buf,int count,MPI_Datatype,int destination,int tag,MPI_Comm comm)
MPI_Recv(void* buf,int count,MPI_Datatype,int source,int tag,MPI_Comm comm, MPI_Status*status)
非阻塞通信模式下的通信和计算与阻塞通信模式下的基本一致,差异之处在于各个进程之间的通讯可能尚未结束时,就已经在进行数据的计算,这样往往可以使CPU在各个核心在通讯的过程中,仍然满载运行,从而减少程序运行的时间,达到并行计算效率的提升。

Figure 1. Communication mode of GEL
图1. GEL格式通讯简图

Figure 2. Communication mode of GER
图2. GER格式通讯简图

Figure 3. Communication mode of AGE
图3. AGE格式通讯简图
在MPI并行环境下,非阻塞通信模式下用到的计算与通讯过程中的命令,如下
MPI_Isend(void* buf,int count,MPI_Datatype,int destination,int tag,MPI_Comm comm, MPI_Request*request)
MPI_Irecv(void* buf,int count,MPI_Datatype,int source,int tag,MPI_Comm comm, MPI_Request*request)
MPI_Waitall(int count,MPI_Request*request,MPI_Status*status)
4. 数值并行计算
为了验证MPI并行环境下交替分组格式的并行效率的提升情况。作如下数值运算。对方程(1),考虑如下初始条件和边界条件,

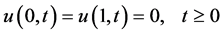
下文给出的数值模拟计算的结果是在双核计算机上进行4进程并行计算得到的运算结果。在上述三种并行有限差分格式下,其中, ,
, ,
,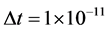 。由于MPI并行消息传递模型并未改变交替分组差分格式的逻辑结构,此处不再赘述方程(1)的数值解的误差分析,而且在文献 [3] 中,亦给出了该类型抛物方程的误差分析状况,在下文中,针对不同的通信模式,得到了两种MPI并行模型在不同进程下的加速比及计算效率。表3~5分别展示了GEL,GER,AGE格式下的MPI阻塞与非阻塞通信模型的程序运算时间,图4显示了运用交替分组格式求解抛物方程,在非并行环境与MPI并行环境下的程序运算时间柱状图。图5给出了4进程并行计算下阻塞通信与非阻塞通信的时间柱状图。表6给出了4进程通信下的并行效率及加速比。
。由于MPI并行消息传递模型并未改变交替分组差分格式的逻辑结构,此处不再赘述方程(1)的数值解的误差分析,而且在文献 [3] 中,亦给出了该类型抛物方程的误差分析状况,在下文中,针对不同的通信模式,得到了两种MPI并行模型在不同进程下的加速比及计算效率。表3~5分别展示了GEL,GER,AGE格式下的MPI阻塞与非阻塞通信模型的程序运算时间,图4显示了运用交替分组格式求解抛物方程,在非并行环境与MPI并行环境下的程序运算时间柱状图。图5给出了4进程并行计算下阻塞通信与非阻塞通信的时间柱状图。表6给出了4进程通信下的并行效率及加速比。
Table 3. The executive time of 4 processes in blocking and non-blocking communication mode for GEL (unit/sec.)
表3. GEL格式下4进程阻塞通信与非阻塞通信模式的程序运算时间比较(单位/秒)
Table 4. The executive time of 4 processes in blocking and non-blocking communication mode for GER (unit/sec.)
表4. GER格式下4进程阻塞通信与非阻塞通信模式的程序运算时间比较(单位/秒)
Table 5. The executive time of 4 processes in blocking and non-blocking communication mode for AGE (unit/sec.)
表5. 交替分组格式下4进程阻塞通信与非阻塞通信模式的程序运算时间比较(单位/秒)
Table 6. Comparison of the parallel efficiency in 4 processes
表6. 不同格式下的4进程并行效率比较

Figure 4. The executive time of single process and 4 processes of AGE blocking communication program
图4. AGE阻塞通信模式下四进程与单进程计算的程序运行时间

Figure 5. The executive time of AGE blocking and non- blocking communication program in 4 processes
图5. 四进程下AGE阻塞通信模式与非阻塞通信模式下的程序运行时间
5. 总结
在上述数值模拟计算的数据表格中,在图4中可以看到,在MPI并行环境中,多条进程运用上述差分格式数值计算抛物方程要比单个进程计算的效率更高。多次试验数据表明,4进程并行计算的时间约是单进程计算的1/4,而且三种差分格式并未出现较大的差别,因为可以在上文中知道,三种差分格式的计算任务量是大致相等的,而MPI并行化处理并未改变计算逻辑,而只是将计算任务分摊,从而达到计算效率的提升。在表3~5与图5中,可以看到MPI阻塞通信对于非阻塞通信的优势,其中,对某一进程来说,非阻塞与阻塞通信的程序计算时间是大致相等的,而非阻塞通信程序的总运算时间是相对较小的,因为非阻塞通信减少了各进程之间的消息传递时间,即通信等待时间,在表3~5中并未给出阻塞通信的通信等待时间,是因为在阻塞通信模型中该时间是无法显示的,不过在实际运算中,阻塞通信的通信等待时间是要高于非阻塞通信的。因此非阻塞通信相对于阻塞通信来说表现出更大的优势。但是,非阻塞通信模型的建立要比阻塞通信更加复杂,这在程序的编码实现上有较多的问题需要解决。在表6还可以看到不同差分格式下的4进程并行效率的比较,可以进一步表明非阻塞通信相对于阻塞通信的优势。即在相同的进程数目下,无论是加速比还是并行效率,非阻塞通信都要高于阻塞通信。
文章引用
高玉羊,顾海明. 求解抛物方程的MPI并行方法
Parallel Methods for Parabolic Equations Based on MPI Implementation[J]. 理论数学, 2017, 07(02): 89-98. http://dx.doi.org/10.12677/PM.2017.72013
参考文献 (References)
- 1. 都志辉, 李三立, 陈渔, 刘鹏. 高性能计算之并行编程技术——MPI并行程序设计[M]. 北京: 清华大学出版社, 2001.
- 2. Quinn, M.J. (2004) Parallel Programming in C with MPI and Open MP. McGraw-Hill, New York.
- 3. Evans, D.J. and Abdullah, A.R. (1983) Group Explicit Methods for Parabolic Equations. International Journal Computer Mathematics, 14, 73-105. https://doi.org /10.1080/00207168308803377
- 4. Saul’yev, V.K. (1965) Integration of Equations of Parabolic Type by the Method of Nets. Proceedings of the Edinburgh Mathematical Society, 14, 247-248. https://doi.org /10.1017/S0013091500008890
- 5. Mohd, A., Norhashidah, H. and Khoo, K.T. (2010) Numerical Performance of Parallel Group Explicit Solvers for the Solution of Fourth Order Elliptic Equations. Applied Mathematics and Computation, 217, 2737-2749.
- 6. Vabishchevich, P.N. (2015) Explicit Schemes for Parabolic and Hyperbolic Equations. Applied Mathematics and Computation, 250, 424-431.
- 7. 张宝琳. 求解扩散方程的交替分段显-隐式方法[J]. 数值计算与计算机应用, 1991, 4: 245-253.
- 8. 张武生, 薛巍, 李建江, 郑纬民. MPI并行程序设计实例教程[M]. 北京: 清华大学出版社, 2009.
- 9. Gorobets, A.V., Trias, F.X. and Oliva, A. (2013) A Parallel MPI + Open MP + Open CL Algorithm for Hybridsuper Computations of Incompressible Flows. Computers & Fluids, 88, 764-772.
- 10. Kellogg, R.B. (1964) An Alternating Direction Method for Operator Equations. Journal of the Society of Industrial and Applied Mathematics, 12, 7. https://doi.org /10.1137/0112072
