Pure Mathematics
Vol.07 No.04(2017), Article ID:21264,5
pages
10.12677/PM.2017.74032
The Identities of M-Gonal Number with Its Application
—M-Gonal Numbers Revisited
Minghao Guo1, Zhicheng Guo2
1School of Biomedical Engineering, Shanghai Jiaotong University, Shanghai
2Dept. Northern Design and Research Institute, Shijiazhuang Hebei

Received: Jun. 17th, 2017; accepted: Jun. 30th, 2017; published: Jul. 6th, 2017

ABSTRACT
In this paper, we present some arithmetic relationships among same-level M-Gonal numbers in a specific situation. We also illustrate some arithmetic relations on M-Gonal numbers who are related with Pythagorean Triangles Number. A few special cases are discussed to obtain some interesting results.
Keywords:M-Gonal Number, Pythagorean Equation, Partitions
M角数恒等式及其应用
—从M角数谈起
郭铭浩1,郭志成2
1上海交通大学生物医学工程学院,上海
2北方设计研究院,河北 石家庄
收稿日期:2017年6月17日;录用日期:2017年6月30日;发布日期:2017年7月6日

摘 要
本文中给出了一些等级相同并满足一定条件的M角数数字关系式。得到了与毕达哥拉斯三角数相关的特殊M角数数字关系式。讨论了一些特殊情况,并得到了一些有趣的结果。
关键词 :M角数,Pythagorean方程,分拆

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
Fermat在Diophtantus的《数论》的空白处写下了第18条评注是下面的命题 [1] 。
命题1:当m ≥ 3时,所有的自然数可表为不超过m个m角数1 (m-gonal number)之和。
命题1中4角数部分抽出来就是下面的命题。
命题2:对任意的自然数n,不定方程
有解。
Euler在知道了Fermat的命题1时颇为激动,然而对命题2的证明颇费周章却不得其解。1772年Lagrange在Euler研究的基础上,利用Euler的四平方恒等式 [2]

证明了命题2,并于1812年证明了命题1。
无论Fermat还是Euler,都对命题1情有独钟。Fermat在所记命题1的空白处,写到了命题1是关系到数论的许多神秘之处,并说关于这一点他自己有写一本书的打算。Euler推导出的四平方恒等式也不是简单的,它使得只需要证明命题2对素数成立。
命题1没有要求自然数表为m个m角数之和。对命题2,就是没有要求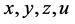 的解都是正整数(有些可以是0)。事实上,形为
的解都是正整数(有些可以是0)。事实上,形为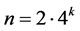 的自然数不能表为4个正整数平方之和。
的自然数不能表为4个正整数平方之和。
更准确的说,我们利用关系式

和命题2推出下面的结论 [3] :
对于n ≥ 169的自然数,都可以表为5个正整数平方之和。
直接验证n < 169的自然数知道:除去下面的12个数,其它的自然数都可以表示为5个正整数平方之和。

结论中的5是不能改进的。
前面结论的逆命题是:
命题3:如果存在一个4角数,可以分别表示为2,3,4,5个相异四角数之和,那么大于这个4角数的所有自然数都可以表示为不超过4个4角数之和 [1] 。
命题3中4个4角数也是不能改进的。逆命题中最重要的一部分条件是:一个4角数拆成了两个相异4角数之和。即勾股定理

我们称“第几个正整数的平方”为“第几项4角数”,那么勾股定理可以解释为:
第13项4角数等于第12项4角数与第5项4角数之和。
当把勾股定理推广到任意m角数的时候,发现了如下的结论:
命题4:第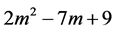 项m角数等于第
项m角数等于第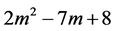 项m角数与第
项m角数与第 项m角数之和。
项m角数之和。
在平方数定义为4角数的情况下,上述结论做为勾股定理的一个推广是合格的2,它实际上是洛伦兹(Lorentz)变换的对偶定理3。顺便说,它也是数学上的质能公式。
2. 应用简介
我们用 表示角数为m的M角数第s项数值,如果我们把m角数的第s项计算公式
表示角数为m的M角数第s项数值,如果我们把m角数的第s项计算公式
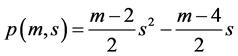
代入上述的结论,很容易推出方程

也就是说,如果方程成立,就证明了上述的结论。然而,讲明白这个方程的符号和数字的物理意义并不是容易的事情 [4] 。从方程的推导过程我们仅仅可以看出,由质能公式确定的空间可以从五维降低到三维。
我们可以用哥德尔数简单解释质能公式如下:第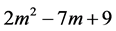 项m角数减第
项m角数减第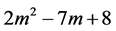 项m角数对应质能公式的∆E,第
项m角数对应质能公式的∆E,第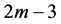 项m角数对应∆mc2,两者数值相等。
项m角数对应∆mc2,两者数值相等。
我们逐渐的会明白,上述结论在形式上是对质能公式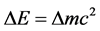 的两边取对数得到的数学公式,它深刻地刻画了物质世界的基本属性 [5] [6] 。并预示着一个物理学上的以下结论:任何系统的平动量与转动量的和是一个定值。物理上的能量守恒定律和动量守恒定律以及万有引力定律都来源于此。
的两边取对数得到的数学公式,它深刻地刻画了物质世界的基本属性 [5] [6] 。并预示着一个物理学上的以下结论:任何系统的平动量与转动量的和是一个定值。物理上的能量守恒定律和动量守恒定律以及万有引力定律都来源于此。
我们得到这些物理上的结论并不奇怪,因为质能公式和它的三次方程在数学上称为自守形式(Automorphic form),它应用到物理上就是各种守恒定律。需要说明的是:守恒定律的个数是有限的,它的最多个数是由自守形式确定的。
3. 一般的整数分拆命题
一般的,第s项的m角数记为 ,拆数
,拆数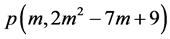 成相异m个m角数的分拆 [7] [8] 种数,通常情况下都大于1。拆数
成相异m个m角数的分拆 [7] [8] 种数,通常情况下都大于1。拆数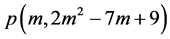 成相异
成相异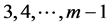 个m角数的分拆种数≥1。例如
个m角数的分拆种数≥1。例如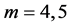
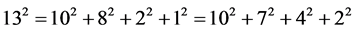

也就是说,4角数(平方数)169拆成4个4角数及5角数852拆成5个5角数的相异分拆种数是2。
它可以推出命题5。
命题5:当 时,m角数的第
时,m角数的第 项,可以分拆为
项,可以分拆为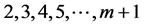 个相异的m角数之和。
个相异的m角数之和。
这个命题的正确性是毋庸置疑的,因为我们只需要重复命题1的证明过程并用哥德尔数解释方程
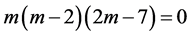
的意义。这种方法略显拙笨,且简化证明过程不属本文的内容。故不再赘述。
由命题5可以推出:所有的自然数都可以表示为不超过m个允许重复的m角数之和。下面给出5角数和6角数的相异分拆。


当 时,第
时,第 项拆成相异2个m角数之和的分拆种数都是1,当自然数N大于等于第
项拆成相异2个m角数之和的分拆种数都是1,当自然数N大于等于第 项m角数
项m角数 时,拆数N成相异3个m角数或更多个m角数之和的相异分拆种数一般情况下都大于1,它们的种数计算依赖于二元数的分拆理论。
时,拆数N成相异3个m角数或更多个m角数之和的相异分拆种数一般情况下都大于1,它们的种数计算依赖于二元数的分拆理论。
4. 分拆理论现状简介及展望——用多个平方和表示的数
在很多文献中,定义多项式幂
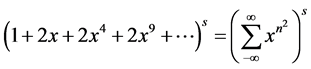
的展开式中,项xt的系数为rs(t)。函数rs(t)表示的是拆数t为s个(注:不一定相异)平方数(4角数)的种数。
拆数t为2,3,4个4角数之和的分拆种数(或者相异种数)人们已经研究的很清楚了。对拆数t为偶数个4角数之和的分拆种数r2k(t)的定量研究,目前多使用椭圆模函数理论,它涉及艰深的算数函数。对于t为奇数r2k+1(t)的定量研究,涉及Legendre符号和广义Jacobi符号
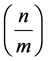
的一个有限和。这些结果许多都是大部头专著 [9] 。
由此可以看出,求解 时,拆数t成相异k个m角数的分拆种数是一个多么困难的问题。但是上述方法都不属于我们要讨论的内容。我们所要寻找的是,怎样用递推的方法求解出拆数t成相异k个m角数的分拆种数。m角数中第
时,拆数t成相异k个m角数的分拆种数是一个多么困难的问题。但是上述方法都不属于我们要讨论的内容。我们所要寻找的是,怎样用递推的方法求解出拆数t成相异k个m角数的分拆种数。m角数中第 项的分拆种数的计算为我们提供了这种可能,其中第
项的分拆种数的计算为我们提供了这种可能,其中第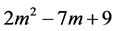 项的
项的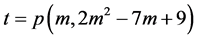 分为两个m角数之和的种数都是1的结果已开先河。
分为两个m角数之和的种数都是1的结果已开先河。
文章引用
郭铭浩,郭志成. M角数恒等式及其应用—从M角数谈起
The Identities of M-Gonal Number with Its Application—M-Gonal Numbers Revisited[J]. 理论数学, 2017, 07(04): 250-254. http://dx.doi.org/10.12677/PM.2017.74032
参考文献 (References)
- 1. Dickson, E.L. (2010) History of the Theory of Numbers. Diophantine Analysis, 2, 6-18.
- 2. Kato, K., Kurokawa, N. and Saito, T. (2005) Number Theory 1: Fermat’s dream. Originally published in Japanese by Iwanami Shoten Publishers, Tokyo.
- 3. 闵嗣鹤, 严士健. 初等数论(第二版) [M]. 北京:北京大学出版社, 2003: 271-275.
- 4. Kato, K., Kurokawa, N. and Saito, T. (2005) Number Theory 2: Introduction to Class Field Theory. Originally published in Japanese by Iwanami Shoten Publishres, Tokyo.
- 5. 牛顿. 自然哲学之数学原理, 宇宙体系[M]. 武汉: 武汉出版社, 1992.
- 6. 俞允强. 广义相对论引论[M]. 第2版. 北京: 北京大学出版社, 1997.
- 7. Euler, L. (1988) Introduction to Analysis of the Infinite. Springer-Verlag, New York. https://doi.org/10.1007/978-1-4612-1021-4
- 8. Koch, H. and Andrews, G.E. (1979) The Theory of Partitions. (Encyclopedia of Mathematics and Its Applications) 2. London-Amsterdam-Don Mills-Sydney-Tokyo, Addison-Wesley Publ. Company 1976. XIV, 255 S. $ 16.50. ZAMM— Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 59, 285-285. https://doi.org/10.1002/zamm.19790590632
- 9. Hardy, G.H. (1981) An Introduction to the Theory of Numbers. The English Language Book Society and Oxford Univ. Pr, London.
NOTES
1M角数是所有角数的统称,m角数指角数为m的数列。
2本结论将指数2推广到了任意正整数(偏序集)。当结论用于平面直角三角形时,就是勾股定理 。当指数s取无穷大时,就是圆周长公式
。当指数s取无穷大时,就是圆周长公式 。
。
3由于洛伦兹(Lorentz)变换是相对论的数学工具,从M角数的平面图可以看出,结论给出的是研究量子理论的数学工具。故称之为洛伦兹(Lorentz)变换的对偶定理。