Pure Mathematics
Vol.
09
No.
02
(
2019
), Article ID:
29225
,
10
pages
10.12677/PM.2019.92021
Qualitative Analysis of Nondivergent Degraded Parabolic Equations with Nonlinear Nonlocal Boundary Condition
Shuwang Xu, Zhuangzhuang Li, Jinzhong Qiu, Meng Li
School of Mathematics and Statistics, Shandong Normal University, Jinan Shandong

Received: Feb. 20th, 2019; accepted: Mar. 6th, 2019; published: Mar. 13th, 2019

ABSTRACT
In this paper, we consider the qualitative analysis of a class of degenerate parabolic equation of non-divergence type with non-linear and non-local boundary conditions. Under the condition of generalized exponential terms, the global existence and blow-up properties of solutions of the equation under various conditions are discussed by using the upper and lower solutions method.
Keywords:Comparison Principle, Upper and Lower Solutions, Degenerate Parabolic Equation of Non-Divergence Type
具有非线性非局部边界条件的非散度型退化抛物方程的定性分析
徐树旺,李壮壮,邱金忠,李萌
山东师范大学数学与统计学院,山东 济南

收稿日期:2019年2月20日;录用日期:2019年3月6日;发布日期:2019年3月13日

摘 要
本文考虑了一类具有非线性非局部边界条件的非散度型退化抛物方程的定性分析问题。在广义指数项条件下,应用上下解方法,讨论了在各种条件下方程解的整体存在性和爆破性质。
关键词 :比较原理,上下解,非散度型退化抛物方程

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文我们讨论具有非局部边界条件的非散度型退化抛物方程
(1.1)
其中 , 是 中具有光滑边界 的有界区域,并作如下假设:
(H1) ,且
;
(H2) 当 时, 是连续非负函数,且 ;
(H3) 。
对具有齐次Dirichlet边界条件的非线性抛物方程解的研究已经有很多结果。例如,在文献 [1] ,Deng等人研究了具齐次Dirichlet边界条件下,非线性方程组的临界指数即 时的退化抛物方程
(1.2)
证明了问题(1.2)没有整体解当且仅当 且 ,这里
是如下线性椭圆问题的唯一正解
(1.3)
然而,有一些重要的物理现象可以用非局部数学模型来解释,例如热弹性力学中的一些现象。在这种情况下,解 描述了每体积材料的熵。自Friedman [2] 对非局部问题的研究以来,人们致力于对具非局部边界条件的抛物方程的解的性质研究。如Lin等人 [3] 中研究了如下形式的问题
(1.4)
作者建立了问题(1.4)作者建立了局部解的存在性、整体存在性和不存在性及爆破性质的讨论解决办法。再者,作者导出了 时的统一爆破估计。
具有局部化源项的非线性抛物方程出现在研究流体通过具有内部局部源的多孔介质的流动以及研究种群动力学等问题中。例如,Chen等人在 [4] 中考虑了如下方程:
(1.5)
在适当的条件下,作者得到了问题(1.5)的爆破准则。当 取特殊情形时,他们还得到了一致爆破估计。
钟光胜在 [5] 中研究了(1.1)当 时的具非线性非局部边界条件的非散度型退化抛物方程的爆破问题。结果表明,非局部边界条件下的抛物方程与齐次Dirichlet边界条件下的抛物方程,具有相类似的爆破速率。
本篇文章在 [5] 的基础上研究了 时某些条件下整体存在性和爆破性,并给出了此类问题的广义比较原理,建立了解整体存在和在有限时刻爆破的条件。结果表明扩散系数 ,尤其是非局部边界条件中的权函数 及非线性指标 对所讨论问题解的整体性和爆破起到了很关键的作用。
我们讨论了上述问题的解的性质,本文的主要结果如下:
定理1.1:假设 ,且 ,
1) 如果 充分小,那么问题(1.1)的解整体存在;
2) 如果 充分大,且存在某个正数 使得 ,那么问题(1.1)的解整体存在。
定理1.2:假设 且 , ,如果 及 足够小,那么问题(1.1)的解整体存在;而如果 及 足够大,且存在某正数 ,使得对关于 积分 ,那么问题(1.1)的解在有限时刻爆破。
定理1.3:假设 , 且 , ,如果对某常数 ,有 ,那么对大初值 ,问题(1.1)的解在有限时刻爆破。
假设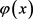 是问题
是问题
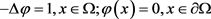 (1.6)
(1.6)
的解。那么有
定理1.4:如果对某常数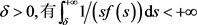 ,且
,且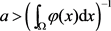 。那么问题(1.1)不存在整体解。
。那么问题(1.1)不存在整体解。
2. 比较原理
下面是关于问题(1.1)上下解的定义,其中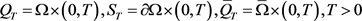 。
。
定义2.1:称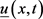 是问题(1.1)在
是问题(1.1)在 上的一个下解,若
上的一个下解,若 ,并满足
,并满足
 (2.1)
(2.1)
类似的,通过改变上式中不等号的方向,可以得到问题(1.1)的上解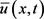 的定义。我们把既是上解又是下解的解称为问题(1.1)的解。
的定义。我们把既是上解又是下解的解称为问题(1.1)的解。
为了建立问题的比较原理。我们先给一个相应的最大值原理 [6] 。
引理2.1:假设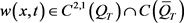 ,且满足
,且满足
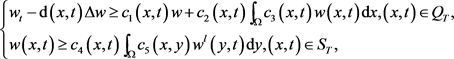 (2.2)
(2.2)
这里 是有界函数,在
是有界函数,在 上
上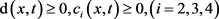 。在
。在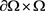 上,
上, 。如果
。如果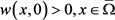 ,则在
,则在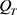 上
上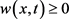 。而且如果
。而且如果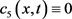 。或者在
。或者在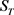 上
上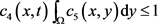 ,在
,在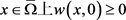 ,那么在
,那么在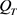 上有
上有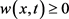 。
。
证明:由于(2.2)式是非局部非退化方程,故我们以完备性给出证明。假设
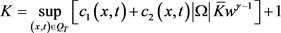 ,其中
,其中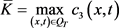 。由于
。由于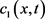 和
和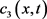 在
在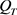 内有界且连续,可知
内有界且连续,可知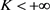 。定义
。定义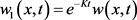 ,由以上变换我们易知
,由以上变换我们易知 。事实上,从(2.2)的第二式和第三式,利用转换式
。事实上,从(2.2)的第二式和第三式,利用转换式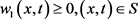 。假定
。假定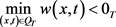 ,从而
,从而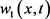 的最小值在
的最小值在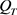 内取得。不失一般性,我们假定最小值在
内取得。不失一般性,我们假定最小值在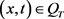 处取得,从而
处取得,从而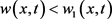 对于任一
对于任一 将
将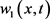 带入(2.2)第一式,得到
带入(2.2)第一式,得到

且有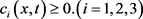 ,并有
,并有 。从而
。从而
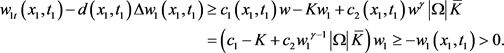
另一方面,注意到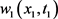 在
在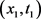 处取到负的最小值且
处取到负的最小值且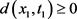 ,于是成立
,于是成立 ,得到矛盾。故
,得到矛盾。故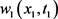 在
在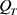 上非负。于是我们可以得到在
上非负。于是我们可以得到在 上
上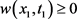 。证讫。
。证讫。
引理2.2:考虑 ,设
,设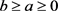 ,
, 且
且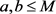 ,其中
,其中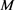 是一正数。若对任意的
是一正数。若对任意的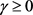 ,
,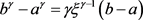 ,则
,则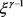 总是一个大于零的有界数。
总是一个大于零的有界数。
证明:若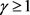 ,则
,则 显然是大于零的有界数,下只讨论
显然是大于零的有界数,下只讨论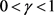 的情形。
的情形。
设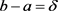 ,
,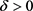 。
。
若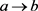 ,则
,则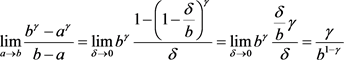 。
。
显然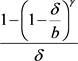 关于
关于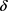 在
在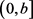 上连续且大于零恒成立,且关于
上连续且大于零恒成立,且关于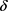 求导易知
求导易知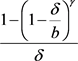 在
在 上递增,所以
上递增,所以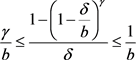 ,从而
,从而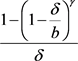 关于
关于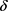 在
在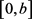 上有界且大于零恒成立。
上有界且大于零恒成立。
从而易知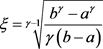 有界且恒大于零,从而
有界且恒大于零,从而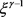 总是一个大于零的有界数。证讫。
总是一个大于零的有界数。证讫。
引理2.3:假设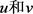 分别是问题(1.1)的非负下解和非负上解,且当
分别是问题(1.1)的非负下解和非负上解,且当 时有
时有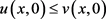 ,如果存在某个正数
,如果存在某个正数 ,使得
,使得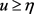 或
或 ,那么在
,那么在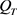 上有
上有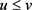 。
。
证明:由于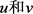 分别是问题(1.1)的非负下解和非负上解,则成立:
分别是问题(1.1)的非负下解和非负上解,则成立:
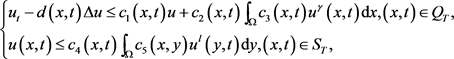
以及

那么在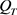 上即有
上即有

这里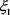 ,
,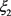 均是介于
均是介于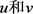 之间的非负数,且因为
之间的非负数,且因为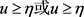 ,所以
,所以 均是大于零的数。
均是大于零的数。
令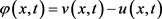 ,则由已知条件
,则由已知条件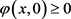 ,且在
,且在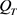 上
上
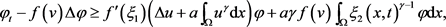
因为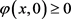 ,
,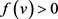 ,
, 在有限空间上有界,由引理(2.2)知
在有限空间上有界,由引理(2.2)知 在有限空间上有界,从而由引理(2.1)即得在
在有限空间上有界,从而由引理(2.1)即得在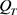 上
上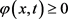 ,从而
,从而 。证讫。
。证讫。
3. 整体存在和有限时刻爆破
定理1.1的证明
1) 设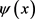 是线性椭圆问题
是线性椭圆问题
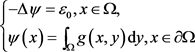 (3.1)
(3.1)
的唯一正解,这里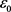 是正常数,并满足
是正常数,并满足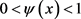 (因为
(因为 ,所以存在这样的
,所以存在这样的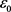 ),并记
),并记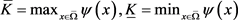 。
。
定义函数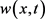 如下:
如下:
 , (3.2)
, (3.2)
这里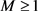 是待定常数。通过计算有
是待定常数。通过计算有
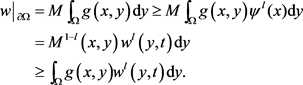 (3.3)
(3.3)
另一方面,对于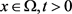 ,
,
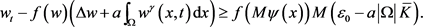 (3.4)
(3.4)
选取 ,并设
,并设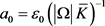 ,那么当
,那么当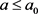 时
时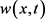 是问题(1.1)的上解。根据比较原理,
是问题(1.1)的上解。根据比较原理,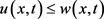 ,因此
,因此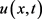 整体存在。证讫。
整体存在。证讫。
2) 考虑常微分方程
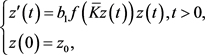 (3.5)
(3.5)
这里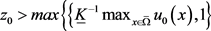 ,
,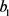 是个待定的正数。根据假设(H3)以及常微分方程理论,问题(3.5)存在唯一解
是个待定的正数。根据假设(H3)以及常微分方程理论,问题(3.5)存在唯一解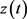 ,而且
,而且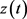 是单调递增的;如果对某个正数
是单调递增的;如果对某个正数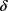 ,有
,有
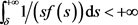 ,那么
,那么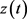 整体存在且
整体存在且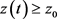 。
。
定义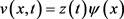 ,其中
,其中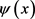 是问题(3.1)的解。
是问题(3.1)的解。
对于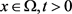 ,我们有
,我们有

对于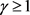 的情形,
的情形,
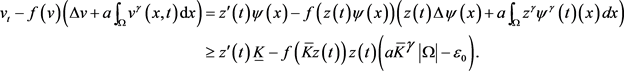 (3.6. A)
(3.6. A)
令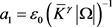 ,令
,令 足够大且满足
足够大且满足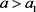 ,则只需取
,则只需取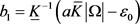 。
。
对于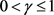 的情形,
的情形,
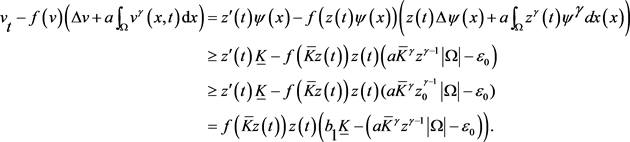 (3.6. B)
(3.6. B)
令 ,令
,令 满足
满足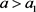 ,且取
,且取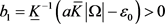 ,仍得
,仍得
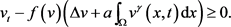 (3.7)
(3.7)
另一方面,对于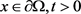 ,有
,有
 (3.8)
(3.8)
这里使用了条件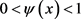 以及
以及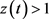 。
。
而对于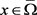 ,有
,有
 (3.9)
(3.9)
这说明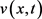 是(1.1)的一个上解。由引理2.3知(1.1)的解整体存在。证讫。
是(1.1)的一个上解。由引理2.3知(1.1)的解整体存在。证讫。
定理1.2的证明
关于解整体存在的证明类似于定理5.1.1中第一种情形。对于任意给定的正数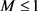 ,定义
,定义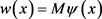 。这里
。这里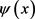 由(3.1)给出。只要问题(1.1)的初值
由(3.1)给出。只要问题(1.1)的初值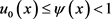 且
且 ,那么
,那么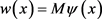 就是问题(1.1)的上解。根据比较原理,问题(1.1)的解整体存在。
就是问题(1.1)的上解。根据比较原理,问题(1.1)的解整体存在。
下面我们证明解的爆破结果。为此,先引入椭圆问题
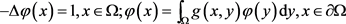 。
。
在假设(H2)及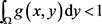 下,上述椭圆问题有唯一正解
下,上述椭圆问题有唯一正解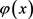 。
。
记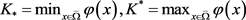 。
。
考虑常微分方程
 (3.10)
(3.10)
则其解 递增且
递增且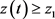 。由于对某个正数
。由于对某个正数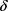 ,有
,有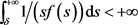 ,因此问题(3.10)的解
,因此问题(3.10)的解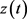 在有限时刻爆破。
在有限时刻爆破。
如果 及
及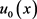 足够大,并满足
足够大,并满足
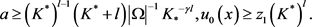
定义函数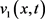 为如下形式:
为如下形式:
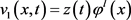 ,
,
对于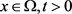 ,
,
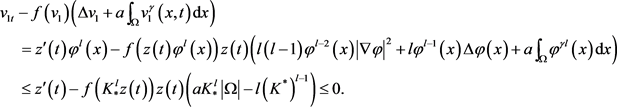 (3.11)
(3.11)
对于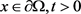 ,根据Jensen不等式有
,根据Jensen不等式有
 (3.12)
(3.12)
而对于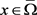 ,可得
,可得
 (3.13)
(3.13)
不等式(3.11)~(3.13)表明 是问题(1.1)的下解。由于
是问题(1.1)的下解。由于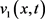 在有限时刻爆破,因此根据比较原理,问题(1.1)的解
在有限时刻爆破,因此根据比较原理,问题(1.1)的解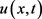 在有限时刻也爆破。证讫。
在有限时刻也爆破。证讫。
定理1.3的证明
设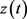 是常微分方程
是常微分方程
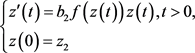 (3.14)
(3.14)
的解,其中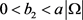 。如果
。如果 是足够大的,并满足
是足够大的,并满足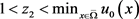 。显然其解
。显然其解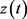 递增且满足
递增且满足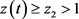 。因此问题(3.14)的解
。因此问题(3.14)的解 在有限时刻爆破。
在有限时刻爆破。
令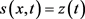 ,则对于
,则对于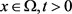 ,有
,有
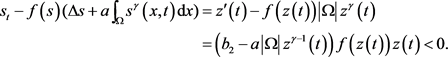 (3.15)
(3.15)
对于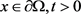 ,有
,有
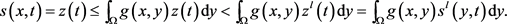 (3.16)
(3.16)
而对于 ,可得
,可得
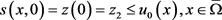 . (3.17)
. (3.17)
不等式(3.14)~(3.17)表明 是问题(1.1)的下解。由于
是问题(1.1)的下解。由于 在有限时刻爆破,因此根据比较原理,问题(1.1)的解
在有限时刻爆破,因此根据比较原理,问题(1.1)的解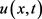 在有限时刻也爆破。
在有限时刻也爆破。
在给出定理1.4的证明之前,我们先介绍如下的引理。
先引入椭圆问题

令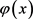 是上述线性椭圆方程问题的特解。
是上述线性椭圆方程问题的特解。
引理3.1:
定义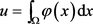 。若
。若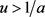 ,则(1.1)正解
,则(1.1)正解 满足
满足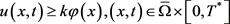 ,其中
,其中 足够小,使得
足够小,使得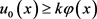 。
。
证明:令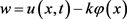 ,
,
则
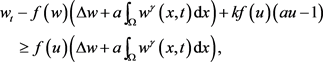
由于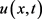 在爆破时间点
在爆破时间点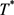 之前有界,依比较原则
之前有界,依比较原则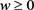 ,即
,即
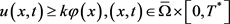 。证讫。
。证讫。
考虑上述线性椭圆方程问题在域 上的情形。
上的情形。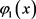 是下面问题的正特解:
是下面问题的正特解:
 ,
,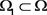 。
。
显然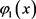 关于
关于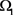 连续,依椭圆方程的比较原理,有
连续,依椭圆方程的比较原理,有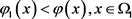 。记
。记
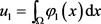 ,则
,则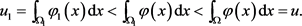
定理1.4的证明
考虑如下问题:
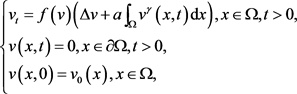 (3.18)
(3.18)
由引理(3.1)及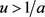 可知存在
可知存在 和
和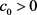 使得
使得
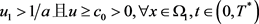 .
.
令
 ,
,
则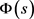 严格单调递减且在
严格单调递减且在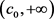 上满足凸性且
上满足凸性且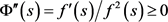 。因此
。因此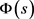 的反函数
的反函数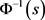 存在且严格单调递减。并满足
存在且严格单调递减。并满足
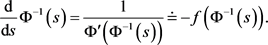 (3.19)
(3.19)
令 。定义
。定义
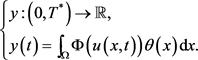
对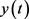 ,
,
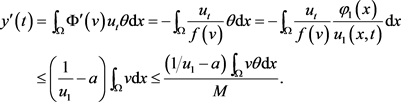
其中 。依
。依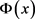 的凸性和Jensen不等式,
的凸性和Jensen不等式,
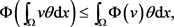
这蕴含着(因为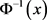 单调递减)
单调递减)
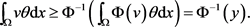
由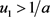 ;
;
记
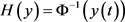 ,
,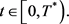
由(3.19)和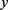 的光滑性,可得
的光滑性,可得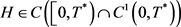 ,且
,且
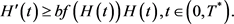 (3.20)
(3.20)
另有
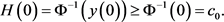
由此,积分(3.20)式从0至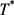 ,得
,得
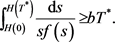 (3.21)
(3.21)
因此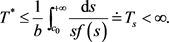
这表明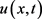 存在时间不会超过
存在时间不会超过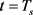 。证讫。
。证讫。
基金项目
山东师范大学本科生科研基金。
文章引用
徐树旺,李壮壮,邱金忠,李 萌. 具有非线性非局部边界条件的非散度型退化抛物方程的定性分析
Qualitative Analysis of Nondivergent Degraded Parabolic Equations with Nonlinear Nonlocal Boundary Condition[J]. 理论数学, 2019, 09(02): 164-173. https://doi.org/10.12677/PM.2019.92021
参考文献
- 1. Deng, W., Li, Y. and Xie, C. (2003) Existence and Nonexistence of Global Solutions of Some Nonlocal Degenerate Parabolic Equa-tions. Applied Mathematics Letters, 16, 803-808.
https://doi.org/10.1016/S0893-9659(03)80118-0 - 2. Friedman, A. (1986) Monotonic Decay of Solutions of Parabolic Equations with Nonlocal Boundary Conditions. Quarterly of Applied Mathematics, 44, 401-407.
https://doi.org/10.1090/qam/860893 - 3. Lin, Z. and Liu, Y. (2004) Uniform Blow up Profiles for Diffusion Equations with Nonlocal Source and Nonlocal Boundary. Acta Mathematica Scientia, 24, 443-450.
https://doi.org/10.1016/S0252-9602(17)30168-6 - 4. Chen, Y. (2011) Blow-Up for a localized Singular Parabolic Equation with Weighted Nonlocal Nonlinear Boundary Conditions. Journal of Mathematical Analysis & Applications, 384, 421-430.
https://doi.org/10.1016/j.jmaa.2011.05.079 - 5. 钟光胜. 几类非线性抛物方程(组)解的性质研究[D]: [博士学位论文]. 镇江: 江苏大学, 2016.
- 6. Deng, K. (1992) Comparison Principle for Some Nonlocal Problems. Quarterly of Applied Mathematics, 50, 517-522.
https://doi.org/10.1090/qam/1178431