Pure Mathematics
Vol.
09
No.
06
(
2019
), Article ID:
31700
,
10
pages
10.12677/PM.2019.96094
Growth of Three Dragons: Model, Numerical Simulation and Visualization
Lizhi Yang, Junyi Zeng, Yixuan Yang
School of Science, Southwest University of Science and Technology, Mianyang Sichuan
Received: Jul. 19th, 2019; accepted: Jul. 29th, 2019; published: Aug. 14th, 2019

ABSTRACT
In this paper, the three fictional dragons Drogon, Viserion and Rhaegal in The Game of Rights are used as prototypes. Under the condition of limited growth resources, the mathematical relationship between the growth of the three dragons and the environmental factors such as climate are considered. The growth of the three dragons was simulated to calculate the various indicators needed for their growth. Finally, sensitivity analysis is performed on it. The model predicts and regulates the competitive growth of multiple species. This keeps the ecological structure of the entire region relatively stable.
Keywords:Competition, Numerical Simulation, Growth Indicator, Sensitivity Analysis
三种龙的生长:模型、数值模拟和可视化
杨枥智,曾钧一,杨羿轩
西南科技大学理学院,四川 绵阳
收稿日期:2019年7月19日;录用日期:2019年7月29日;发布日期:2019年8月14日

摘 要
本文以《权利的游戏》中三条虚构的龙Drogon,Viserion和Rhaegal为原型,在生长资源有限的条件下,综合考虑三条龙在生长过程中的竞争关系以及气候等环境因素,建立数学模型并数值仿真了三条龙的生长状况,借此计算出其生长所需的各种指标,最后对其进行灵敏度分析。该模型可对多个物种竞争的生长情况进行预测并加以调控,使整个区域的生态结构保持相对稳定。
关键词 :竞争,数值仿真,生长指标,灵敏度分析

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
不论对于东方人还是西方人,龙这一传说中的物种都是大家耳熟能详的。地球从古至今是否真正地诞生过这种生物历来众说纷纭,抛开龙的真实性不提,本文仅仅从设想它为假定的欧洲怪物谈起。
由于龙是虚构的生物,故本文需要在一定的现实基础上进行建模,例如某些动物的生长模型和种群竞争。蔡永华 [1] 等在2016年运用Logistic、Bertalanffy、Gompertz模型对圈养林麝体质量、体尺进行生长曲线拟合,结果表明3种模型均能很好地拟合周龄与体质量之间的回归关系。张媛等 [2] 在2009年用Logistic拟合马头山羊体重生长曲线,其拟合度(R2)均大于0.99能很好地拟合马头山羊的生长曲线。陶志伦,项云 [3] 在2004年以Logistic和Gompertz方程拟合了90头金华猪生长肥育期的生长曲线,结果表明,Logistic和Gompertz方程均可拟合金华猪生长曲线。Nahashon S. N等 [4] 在2006年运用Logistic和Gompertz模型拟合珍珠鸡生长曲线,发现Logistic模型较符合雌性珍珠鸡的生长曲线。综上所述,本文以Logistic为基础展开对龙的生长状况的讨论。
2. 问题分析
根据史诗奇幻小说《冰与火之歌》改编的虚构电视剧《权力的游戏》,“龙之母”丹妮莉丝·坦格利安养大了三条龙,分别叫Drogon,Rhaegal与Viserion。它们孵化出来很小,大约10 kg,一年后会长到30~40 kg。它们一生都在生长,这取决于它们所处的环境和食物的数量。
考虑这三条虚构的龙现在还活着,假设上述龙的基本生物学特征是准确的,本文的任务是分析龙的特征,行为,习惯,饮食,以及与环境的互动。因为龙是一个虚构的生物,所以在分析问题之前我们需对龙做一些额外的假设,例如,龙能够飞很远的距离,呼吸火焰,并抵抗巨大的创伤等。
我们需要提前解决这些问题:1) 龙的生态影响和需求;2) 龙的能量支出;3) 龙的卡路里摄取量;4) 支撑三条龙需要的面积;5) 为龙提供不同级别援助的社区的大小;6) 气候条件是否会对维持和生长一条龙所需的资源产生重大影响。
3. 多因素生长模型
3.1. 模型分析
本文综合考虑外部环境因素和资源竞争因素分析对的生长状况。龙的体重增长率与龙自身的能量摄取率,能量消耗率,生活面积有关。面积足够时,它们和平共处,保持各自的生长曲线;面积不足时,三条龙会因为资源的短缺而发生争斗,形成竞争关系。这就需要求出三条龙和平生长以及发生争斗的临界面积,即三条龙恰好正常生长的最小面积,然后分情况讨论它们的体重增长情况。
其一,面积足够时外部因素对生长发育的影响。首先考虑一条龙的生长,在Logistic模型的基础上进行改进 [5] ,引入外部环境影响因素。不同季节和气候会对龙的能量消耗,资源摄取量以及生存的面积有不同的要求。季节对龙的资源供给是呈周期变化的,故应引入周期函数来表示季节对资源供给的影响。同时,由于随机因素的影响,故引入随机量 。
其二,面积资源不足时,龙之间存在竞争关系。它们凭自己的能力争取生活面积,尤其是在冬季食物匮乏的情况下,它们会入侵对方领域,抢夺食物。故引入竞争因素,对三条龙的生存情况进行模拟分析。它们的相互竞争关系如图1所示。

Figure 1. Overview of the three dragons’ distribution
图1. 三条龙的分布概况图
3.2. 模型建立
Step1:环境资源充足时,确定临界面积
为确定临界面积,在Logistic模型的基础上引入气候、季节、面积因素u,对应的体重增长率为:
(1)
其中, , 控制了龙的体重生长面积,u是关于 的函数,而增长率 随季节呈
周期变化,故考虑正弦函数,最终确定
(2)
式(2)对应的大致图像如图2所示,表示季节的周期变化对资源供给率的影响:
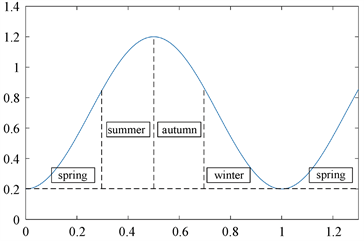
Figure 2. Diagram of the relationship between resources and seasons
图2. 资源与季节之间的关系图
其中, 保证变化范围是非负的,由上图可知,夏冬季节资源给予率较高,春冬季节资源给予率较低但始终高于某一正常数值b。将(2)式导入(1)式得:
(3)
综上,得到如下改进Logistic模型:
 (4)
(4)
其中 表示自身能量摄取率, 表示生存面积, 表示单位面积资源给予率。
利用(4)式可以求出供每条龙生长的临界面积 ,则供三条龙和平共处的总面积为:
(5)
Step2:综合环境和竞争因素模拟龙的生长情况
当面积不足,资源短缺时,考虑龙的竞争生长模型,即其他龙对一条龙生长的抑制作用,(4)式转化如下:
(6)
又因为一条龙生长过程中会遇到无法预料的偶然因素,故引入随机量 ,且 ,得:
(7)
其中 为年增长率。
综合考虑季节气候因素,竞争因素和随机影响因素得到三条龙的多因素生长模型如下:
(8)
其中, 表示第i条龙的自身能量摄取率,对龙的生长起促进作用, 表示第i条龙与第j条龙竞争时第j条龙的能量消耗率。
3.3. 模型的求解与分析
限定条件为龙的生长在40岁左右体重值开始趋于稳定,从而确定供给龙正常生长的最小面积。运用四阶Runge-Kutta算法 [6] 进行数值模拟,得到一条龙的体重生长曲线如图3所示。
由图3可以看出,龙的生长在每一年内呈周期性增长,夏秋季节增长较快,春冬季节增长较缓慢。由于随机因素影响,曲线虽有微小波动,但总体呈增长趋势,并且体重增长在40岁左右开始趋于平缓。
为了确定三条龙各自所需的临界领地面积,需对三条龙的体重上限 ,单位面积资源供给率 ,自身能量摄取率 和资源给予常量b进行多次取值,对应的参数表如表1所示。
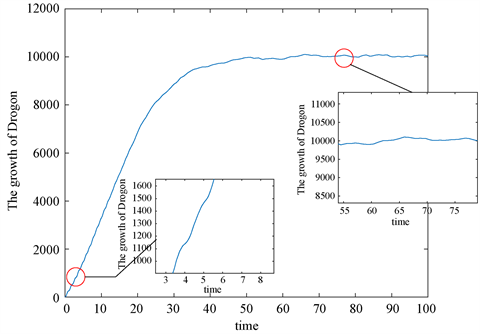
Figure 3. The weight gain of a dragon growing
图3. 一条龙成长生长的体重增加图
Table 1. Corresponding parameter table
表1. 对应的参数表
通过数值模拟得到三条龙的临界面积分别为: ,供三条龙生长的总面积为 。
由结果可知,Drogon所占领的北极地区面积最大,Viserion在干旱地区,面积次之;Rhaegal在暖温带地区,占地面积最小。由于北极地区气候较冷,草木生长较慢甚至困难,所以在同等条件下Drogon比Viserion与Rhaegal占地面积大才能保证其自身生长的需要,而暖温带地区气候环境适宜,食物充足,故Rhaegal所需面积较小。
当 时,三条龙之间不存在竞争关系,当 时,龙之间会产生资源的竞争,此时综合考虑季节气候因素,竞争因素和随机影响因素对三条龙的生长情况进行数值模拟,结果如图4所示。
由图4可以看出,竞争情况下 Rhaegal处于优势地位,Viserion次之,而Drogon有濒临死亡的危险。这可能是因为Drogon生活环境较其他两条龙较为恶劣,所以在竞争中处于劣势地位,由于自然生存的弱肉强食而死亡。
4. 基于外界援助的多因素生长模型
由模型三的数值模拟可知在进行生存竞争后,Rhaegal处于优势地位,生长状况最好。Viserion生长一般,但是Drogon在13年时会死亡。但是我们的目的是三条龙都能较好地生长,且生长趋势大抵相同。所以对于龙的生长,需要外界因素的介入(比如人的援助等)。对于三条龙的生长,在具体量化时外界因素时,主要分两个方面,一个是提高龙自身的能量摄取率,以促进它们的生长;一个是尽可能的阻止它们的竞争,减少能量消耗率。综上讨论,在模型三的基础上引入外界因子,得如下模型:

Figure 4. Growth conditions of three dragons under multi-factor conditions
图4. 三条龙在多因素条件下的生长状况图
(9)
其中 取值范围为 ,表示对Drogon和Viserion的能量摄取率的增加量。 取值范围为 ,表示三条龙互相竞争时自身能量消耗率的减少量。
选取各参数如下:
(10)
借助MATLAB2018a进行多次数值模拟,得到三条龙的生长状况如图5所示。
由图5可知,在第18年左右之前的第一阶段幼年期,三条龙的体重虽局部有些微小波动,但整体上都在迅速增长。其中Rhaegal和Viserion生长状况类似,比较良好,但是相对而言Drogon体重增加量比其他两条龙低,且在第18年左右时,Rhaegal和Viserion体重大抵相当。第18年到55年左右的第二阶段的中年期,三条龙的体重也在增长。其中Viserion的生长状况最好,Rhaegal次之。需要注意的是Drigon生长依旧迅速,在第55年左右其体重与Rhaegal相差不大。第55年到100年左右的第三阶段的老年期,三条龙的体重增长逐渐减缓,虽然由于一些无法预知的外界因素,其体重有一些轻微抖动,但最终稳定在同一个阈值左右。这说明三条龙最终都得到了正常生长。
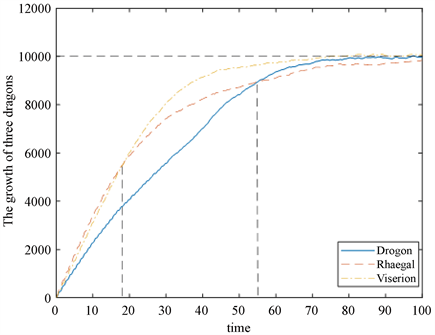
Figure 5. Growth status diagram of external factors
图5. 外界因素介入的生长状况图
由上述分析可以看出,通过外界因素的介入,具体而言就是增加竞争弱势龙的自身能量摄取率,尽量阻止它们的相互竞争,减少因竞争产生的自身能量消耗率,最终使得三条龙都能够正常生长。
在基于外界援助的多因素生长模型的基础上,现讨论三条龙正常生长所需要的年平均能量摄取量 ,年平均能量消耗量 ,以及外界援助的年平均能量援助量 。
三条龙的年平均能量摄取量的数学表达式为:
(11)
其中,Y为常数。
三条龙的年平均能量消耗量的数学表达式为:
(12)
外界援助的年平均能量援助量:
(13)
由于三条龙的体重与时间的函数关系无法求出解析式,故运用MATLAB2018a数值近似计算。计算结果为三条龙Drogon,Rhaegal和Viserion正常生长的年平均能量摄取量分别为5.36 × 106 cals,3.43 × 106 cals和4.96 × 106 cals;年平均能量摄取量分别为4.08 × 106 cals,3.14 × 106 cals和3.80 × 106 cals。而外界给予Drogon和Viserion的年平均能量援助量为2.81 × 106 cals和2.34 × 106 cals。
5. 灵敏度分析
1) 考虑在竞争时,Drogon和Rhaegal竞争比较激烈。在模型三的基础上,设置Drogon和Rhaegal自身能量消耗率分别为0.18和0.19。数值仿真结果如图6所示,可见Drogon不敌Rhaegal,在6.5年左右时死亡。
2) 考虑在竞争时,三条龙竞争都比较激烈。在模型三的基础上,在自身能量消耗率方面,设置Drogon为0.18和0.19;Rhaegal为0.19和0.18;Viserion为0.2和0.18。数值仿真结果如图7所示,可见Drogon和Viserion在竞争中处于劣势,且Drogon在6年左右时死亡,只有Rhaegal和Viserion存活下来。

Figure 6. Competitive survival simulation diagram a
图6. 竞争生存模拟图a
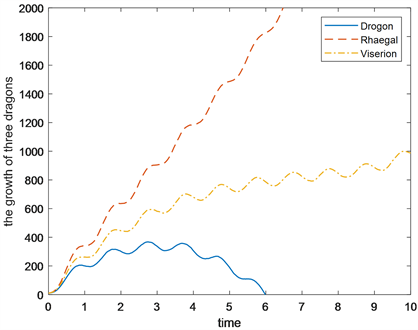
Figure 7. Competitive survival simulation diagram b
图7. 竞争生存模拟图b
3) 考虑在竞争时,三条龙所在领地不同。在模型三的基础上,设置三条龙Drogon, Rhaegal, Viserion自身所在领地面积分别为6000,2000和500。数值仿真结果如图8所示,可见Viserion在竞争中处于劣势,在6年左右时死亡,Drogon和Rhaegal存活下来。
4) 考虑在竞争时,三条龙所在领地的单位面积资源给予率不同。在模型三的基础上,设置三条龙Drogon,Rhaegal,Viserion自身所在领地的单位面积资源给予率分别为0.2,0.2和0.6。数值仿真结果如图9所示,可见Viserion在竞争中存活一段时间后,在16年左右时死亡。Drogon和Rhaegal存活下来。
5) 考虑在竞争时,三条龙领地面积较小,生存资源有限,竞争较为激烈。在模型三的基础上,设置三条龙Drogon,Rhaegal,Viserion自身所在领地面积均为1000;单位面积资源给予率分别为0.05,0.04和0.06;在自身能量消耗率方面,设置Drogon为0.28和0.29;Rhaegal为0.29和0.28;Viserion为0.3和0.28。数值仿真结果如图10所示,可见三条龙都无法正常生长,并且Rhaegal在第4年就死亡。
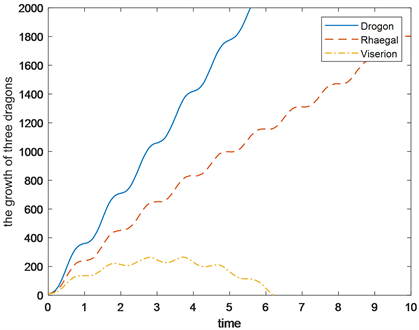
Figure 8. Competitive survival simulation diagram c
图8. 竞争生存模拟图c

Figure 9. Competitive survival simulation diagram d
图9. 竞争生存模拟图d

Figure 10. Competitive survival simulation diagram d
图10. 竞争生存模拟图d
6. 结论
生物生长模拟模型是对所研究的生物–竞争–环境系统中生物的生长发育及生长形成与外界环境的动态与概要描述。由于生长系统的复杂性,因此大多数生长模型是在某种理想水平上建立起来的。本文引入了龙这个虚拟的生物,在经典Logistic模型的基础上添加环境–竞争因子,并采用了一个带有偏置项的周期函数 来量化季节气候对龙生长的资源给予率的周期性变化,使其作为在拟合生物模型上更加的准确。在今后的研究中,这种方法可推广应用到很多领域,凡与生长因素有关的因子,都可用这种方法进行模拟。并且可将本文的研究思路与方法应用不同的生物上,做出进一步的仿真。
文章引用
杨枥智,曾钧一,杨羿轩. 三种龙的生长:模型、数值模拟和可视化
Growth of Three Dragons: Model, Numerical Simulation and Visualization[J]. 理论数学, 2019, 09(06): 702-711. https://doi.org/10.12677/PM.2019.96094
参考文献
- 1. 蔡永华, 杨营, 付文龙, 等. 圈养林麝生长曲线拟合[J]. 四川动物, 2016, 35(2): 238-242.
- 2. 张媛. 马头山羊生长发育及繁殖性状遗传参数估计研究[D]: [硕士学位论文]. 长沙: 湖南农业大学, 2010: 1.
- 3. 陶志伦, 项云. 金华猪生长曲线探讨[J]. 浙江农业学报, 2004, 16(2): 99-101.
- 4. Nahashon, S.N., Aggrey, S.E., Adefope, N.A., Amenyenu, A. and Wright, D. (2006) Growth Characteristics of Pearl Gray Guinea Fowl as Predicted by the Richards, Gompertz, and Logistic Models. Poultry Science, 85, 359-363.
https://doi.org/10.1093/ps/85.2.359 - 5. 司守奎, 孙兆亮. 数学建模算法与应用[M]. 第2版. 北京: 国防工业出版社, 2016: 109-114.
- 6. 丁丽娟, 程杞元. 数值计算方法[M]. 北京: 高等教育出版社, 2011: 300-305.
