Pure Mathematics
Vol.
09
No.
10
(
2019
), Article ID:
33464
,
8
pages
10.12677/PM.2019.910142
The Isolated Properties of KdV Equation in Nerve Cell Impulse Conduction
Jie Yang, Bing Xiao*
School of Mathematics Sciences, Xinjiang Normal University, Urumqi Xinjiang

Received: Nov. 26th, 2019; accepted: Dec. 9th, 2019; published: Dec. 16th, 2019

ABSTRACT
In this paper, the homogeneous equilibrium method is mainly used to solve the KdV equation that nerve cell impulse conduction should satisfy, and further verify that nerve cell impulse conduction is an isolated wavelet, so as to analyze the properties and significance of the isolated wavelet of nerve cell impulse conduction. From a medical point of view, the diagnosis of nerve cell lesions can be assisted by detecting the parameters of nerve cell pulse conduction solitary wavelet.
Keywords:Homogeneous Equilibrium Method, Kdv Equation, Solito

KdV方程在神经细胞脉冲传导的孤立子性质
杨洁,肖 冰*
新疆师范大学数学科学学院,新疆 乌鲁木齐

收稿日期:2019年11月26日;录用日期:2019年12月9日;发布日期:2019年12月16日

摘 要
本文主要是通过利用齐次平衡法来求解神经细胞脉冲传导应满足的KdV方程的解,并进一步去验证神经细胞脉冲传导是孤立子波,从而分析神经细胞脉冲传导的孤立子性质及其意义。从医学的角度来看,可以通过检测神经细胞脉冲传导孤立子波的参数来辅助诊断神经细胞的病变。
关键词 :齐次平衡法,KdV方程,孤立子

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
微积分创立不久,人们研究微积分时,出现的微积分的分支偏微分方程。到18世纪已经相继研究弦振动方程、调和方程与热传导方程等著名的方程。19世纪中叶,随着对具体方程的研究,逐渐形成偏微分方程的一般理论。进入20世纪以来,随着数学科学的发展、计算机的普及与计算方法的创新,其在理论与应用方面都取得巨大的成效。可以说偏微分方程起源于18世纪,发展于19世纪,兴盛于20世纪。
英国科学家司各特·罗素(John Scott Russell, 1872.5.18~1970.2.2) 1884年在《论波动》一文中记述了他在1834年观察到的一种水波现象,他将这种始终保持在水面上向前平移的孤立水峰称为孤立波,并认为这是浅水波运动的一种稳定解。1895年瑞典数学教授柯特维格(D. J. Korteweg)和他的学生德佛累斯(G. deVries)研究了浅水波的运动,并在论文中提出了一个数学模型方程,即后来著名的柯特维格–德佛累斯(KdV)方程 [1] [2] [3]。随着对非线性问题研究的深入,人们发现相当广泛的一类描述非线性作用下的波动方程或方程组均可归为KdV方程,并且一大类非线性偏微分方程有孤立波解(又称为孤立子)。
1952年艾伦·劳埃德·霍奇金(Hodgkin, 1914~1998,英国)和安德鲁·菲尔丁·赫胥黎(Huxley, 1917.11.22~2012.5.30,英国)通过对神经纤维中神经冲动传播的研究提出了Hodgkin-Huxley模型(简称H-H方程) [4]。20世纪50年代中期,理查德·菲茨休(Fitz Hugh)开始致力于寻找一种可以简化H-H模型的方法,1964年,南云(Nagumo)在FitzHugh的基础上从实验角度成功化简了H-H方程,并称之为FitzHugh-Nagumo方程 [5]。
2. 研究对象与方法
2.1. 研究对象
霍奇金(Hodgkin, 1914~19998)与赫胥黎(Huxley, 1917.11.22~2012.5.30)通过实验表明鱿鱼的神经脉冲的类型和速度可以看作是方程 的数值解,其中f是关于u的一个相当复杂的泛函,它的具体精确形式没有确切地给出来。但是可以知道这种模型所显示的神经主要特征是脉冲要么迅速的衰减下去要么就像行波一样形成一种特征形状然后沿直线传播并且不变形。后来Nagumo提出了一个满足这种行为的更简单的模型 (其中f是形如 , 的一个三次多项式,参数a是由细胞膜的电特性决定并与细胞膜性质相关的参数,b是一个正的常数, 是一个不定积分)中发现了这种行为 [6]。我们令参数 则可以得到简化的FitzHugh-Nagumo方程 ,在文献 [7] [8] [9] [10] 中分别给出了不同情形下神经细胞脉冲传导及大动脉血管中孤波特性。本文旨在通过该方程 ,利用齐次平衡法 [11] 来求出其孤立子解并研究其性质。
2.2. 方法
对简化的FitzHugh-Nagumo方程
(2.1)
为使非线性项与最高阶导数项达到平衡,设(2.1)具有如下形式的解
(2.2)
其中 , 是待定函数,c为待定常数。
由(2.2)容易计算出
(2.3)
将(2.3)代入(2.1)并将 的相同导数及其最高次幂项放在一起可得:
(2.4)
令(2.4)中 的系数为零,于是 应满足常微分方程
. (2.5)
则可以得到(2.5)的两个解 为了简便,我们先取
(2.6)
那么则有如下关系
(2.7)
将(2.2)中 取作(2.6),并利用(2.7),则(2.4)变为:
令 , 的系数及常数项分别为零,得 ,c满足如下的方程组:
(2.8)
由于齐次方程具有指数形式的解,按照齐次平衡法,可以假设 具有下列形式的解:
(2.9)
其中 , 为待定常数,并将其代入(2.8)则可以得到
(2.10)
解(2.10)可得 ,1或a。
下面分三种情况讨论简化的FitzHugh-Nagumo方程的孤波解。
情形1当 时,由(2.10)可得到
从而可以解得 ,。
,再由(2.2)可得 。
最终可以获得方程(2.1)的第一组孤立波解:
,。
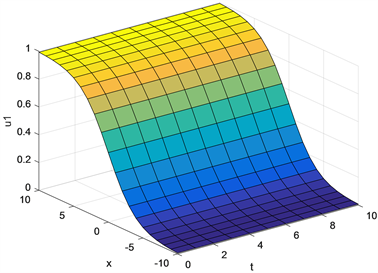
Figure 1. The graph of when
图1. 当 时 的图像
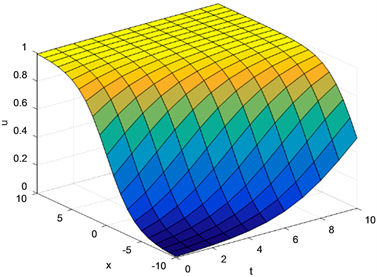
Figure 2. The graph of when
图2. 当 时 的图像
情形2当 时,由(2.10)可得到
,。
从而可以得 ,再由(2.2)可得到方程(2.1)的第二组孤波解:
,其中 。

Figure 3. The graph of when
图3. 当 时 的图像
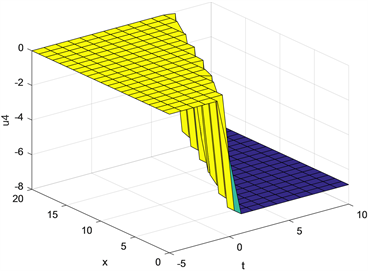
Figure 4. The graph of when
图4. 当 时 的图像
情形3当 时,由(2.10)可得
,。从而有 ,再由(2.2)可以得到方程(2.1)的第三组孤立波解:
,其中 。

Figure 5. The graph of when
图5. 当 时 的图像
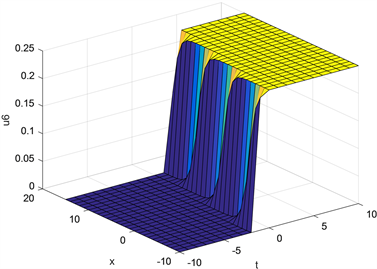
Figure 6. The graph of when
图6. 当 时 的图像
同理可得,当 时可以得到同样的结果。
3. 结果与讨论
在第二部分中我们用MATLAB软件来刻画了神经脉冲传导的孤波的膜电压 与空间x和时间t的关系(图1~6),从图中可以看出神经细胞脉冲是形成的一种典型的沿着神经元的轴突传导下去的形式。再取 ,从第一组孤波解出发来做出在这种情况下神经细胞脉冲传导的孤立子波的形态,如图7和图8。
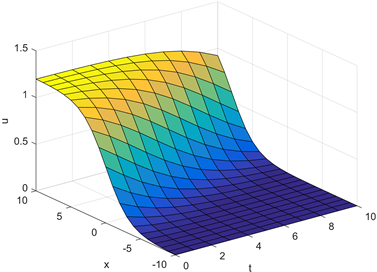
Figure 7. The graph of when
图7. 当 时 的图像
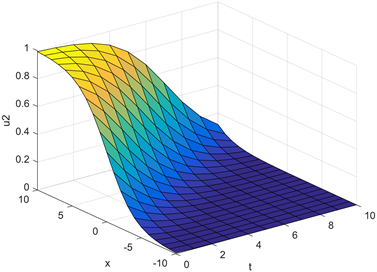
Figure 8. The graph of when
图8. 当 时 的图像
通过对图1、图2与图7、图8的比较我们可以看出当参数a发生改变时,其神经细胞脉冲的孤立子波的波速、振幅都会随之发生相应的变化,同理可以得到当 时第二组与第三组孤波解的图像,由于篇幅的限制在此就不一一给出。我们知道参数a是由细胞膜的电特性决定并与细胞膜性质相关的参数并且 ,由此我们可以得出当人体内的神经细胞发生病变时,其神经细胞脉冲的孤立子波的波速、振幅都会随之发生相应的变化。
因此在医学角度上可以通过借助于FMRI (磁共振成像)等一些医学仪器来描绘出神经细胞脉冲传导的孤波的膜电压随时间和空间的变化图像,从而可以检测出神经细胞脉冲孤立子波的一些参数的变化,进而可以达到辅助诊断神经细胞病变的目的。
文章引用
杨 洁,肖 冰. KdV方程在神经细胞脉冲传导的孤立子性质
The Isolated Properties of KdV Equation in Nerve Cell Impulse Conduction[J]. 理论数学, 2019, 09(10): 1159-1166. https://doi.org/10.12677/PM.2019.910142
参考文献
- 1. 王定江. 应用偏微分方程[M]. 杭州: 浙江大学出版社, 2007.
- 2. 郭柏灵, 苏凤秋. 孤立子[M]. 沈阳: 辽宁教育出版社, 1998.
- 3. 包霞, 斯仁道尔吉. 孤立子理论在中国的早期发展——纪念中国孤立子理论研究40周年[J]. 数学的实践与认识, 2019, 49(2): 279-285.
- 4. Hodgkin, A.L. and Huxley, A.F. (1952) A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve. Journal of Physiology, 117, 500-544. https://doi.org/10.1113/jphysiol.1952.sp004764
- 5. Fitzhugh, R. (1961) Impulse and Physiological States in Theoretical Models of Nerve Membrane. Biophysical Journal, 1, 445-466. https://doi.org/10.1016/S0006-3495(61)86902-6
- 6. Mckean, H.P. (1970) Nagumo’s Equation. Advances in Mathematics, 4, 209-223. https://doi.org/10.1016/0001-8708(70)90023-X
- 7. 李向正, 张卫国, 原三领. 神经脉冲传播的一种特殊模型的研究[J]. 生物医学工程学杂志, 2010, 27(5): 1142-1145.
- 8. 胡建峰, 王锦丽, 包学才. 含损耗神经脉冲传输的耦合孤波特性[J]. 中国组织工程研究与临床康复, 2009, 13(30): 5911-5914.
- 9. 柴玉珍, 张建文, 杨桂通. 神经脉冲波传播形态的研究[J]. 生物医学工程学杂志, 2008, 25(5): 1184-1188.
- 10. 岳超, 刘照军, 张敬军, 等. 大动脉血管中孤立子波的性质分析[J]. 中泰山医学院学报, 2015, 36(2): 121-123.
- 11. 范恩贵, 张鸿庆. 非线性孤子方程的齐次平衡法[J]. 物理学报, 1998, 47(3): 353-362.
NOTES
*通讯作者。