Applied Physics
Vol.07 No.05(2017), Article ID:20778,6
pages
10.12677/APP.2017.75022
Peng Wang, Ju Zhou, Tianyi Cai, Sheng Ju
College of Physics, Optoelectronics and Energy, Soochow University, Suzhou Jiangsu

Received: May 8th, 2017; accepted: May 24th, 2017; published: May 27th, 2017

The Crystal Structure and Electronic Structure of Ferroelectric PbTiO3: A Hybrid Functional Approach
ABSTRACT
Based on the hybrid functional theory, we investigated the effect of the long range Hartree-Fork term on the crystal structure and electronic structure of ferroelectric PbTiO3. It is found that the band gap based on the PBE exchange correlation potential with α of 0.325 is in agreement with experimental result. In addition, we studied the influence of α on the crystal structure with PBE and PW exchange correlation potential, respectively. We found that PW could give a reasonable crystal structure when α is around 0.2. The band gap here, however, is less than the experimental value. Therefore, these findings indicate that the hybrid functional approach may be not suitable for ferroelectric PbTiO3.
Keywords:Band Gap, Hybrid functional, First Principles, PbTiO3
铁电材料PbTiO3晶体结构和电子结构的 杂化泛函研究
王鹏,周琚,蔡田怡,雎胜
苏州大学物理与光电·能源学部,江苏 苏州
收稿日期:2017年5月8日;录用日期:2017年5月24日;发布日期:2017年5月27日

摘 要
基于杂化泛函理论,我们考察了长程Hartree-Fork项在交换关联势中所占比例(α)对铁电材料PbTiO3晶体结构和电子结构的影响。我们发现基于PBE交换关联势,当α等于0.325时杂化泛函所得的带隙值与实验结果相吻合。另外,基于PBE和PW交换关联势我们分别研究了α对晶体结构的影响,基于PBE交换关联势的结果与实验值相差较大。而基于PW交换关联势的计算表明,当α等于0.2时,计算所得到的晶体结构与实验结果比较吻合,但此时带隙值却小于实验值。这些结果表明杂化泛函对于铁电材料PbTiO3的适用性还有待商榷。
关键词 :带隙,杂化泛函,第一性原理,PbTiO3

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
钙钛矿型的铁电氧化物,如PbTiO3和Pb(Zr, Ti)O3固溶体,均属于电子陶瓷材料,其具有铁电性及大的压电响应和高介电常数等相关机电性能 [1] 。由于其优越的性能,铁电钙钛矿氧化物在器件方面的应用已引起广泛地关注,如高密度非易失性随机存取存储器、传感器、机电设备等 [2] [3] 。
第一性原理计算方法在预测材料性质方面起着非常重要的作用。虽然传统的基于局域密度近似 [4] 和广义梯度近似 [5] 的计算方法可以较好地预测材料基态的物理性质,但计算得到的带隙与实验值并不符合。最近人们已经应用杂化泛函理论来研究一些氧化物 [6] 的物理性质,包括VO2、V2O3、Ti2O3、LaTiO3和YTiO3等,而且得到与实验比较吻合的结果 [7] [8] [9] [10] 。然而,对于铁电材料而言,基于杂化泛函的第一性原理研究还比较少。本文以铁电材料PbTiO3为例,利用杂化泛函理论研究其块体材料的晶体结构和电子结构。我们发现基于PBE交换关联势,当长程Hartree-Fork关联项为0.325时杂化泛函所得的带隙值与实验结果相吻合。基于PBE交换关联势所得的晶体结构与实验值相差较大,而基于PW交换关联势的计算表明,当长程Hartree-Fork关联项等于0.2时,杂化泛函所得的晶体结构与实验结果比较吻合,但此时带隙值小于实验值。
2. 计算方法
我们使用基于投影缀加平面波方法(PAW)的第一性原理软件包VASP [11] [12] 。采用基于PBE [13] 和PW [14] 交换关联势以及考虑长程Hartree-Fork项作用的杂化泛函方法 [15] 来研究PbTiO3的晶体结构和电子结构。我们考虑Pb6s26p24个价电子,Ti4d35s14个价电子,O 2s2p46个价电子的贡献。平面波截断能量为600 eV。k点网格为6 × 6 × 6。收敛标准为10−5 eV。在杂化泛函理论中,我们用Hartree-Fock交换项来替换部分短程的PBE(PW)交换势, 具体表达式如下:
 (1)
(1)
其中α是Hartree-Fock项所占比例。在计算过程中,我们考察不同α值对PbTiO3电子结构和晶体结构的影响,寻找与实验相符合的α值。
3. 计算结果与讨论
图1为PbTiO3的晶体结构图。左图为铁电相,右图为顺电相。其中黑色为Pb元素,蓝色为Ti元素,红色为O元素。表1为PbTiO3晶体结构的实验值 [16] 。
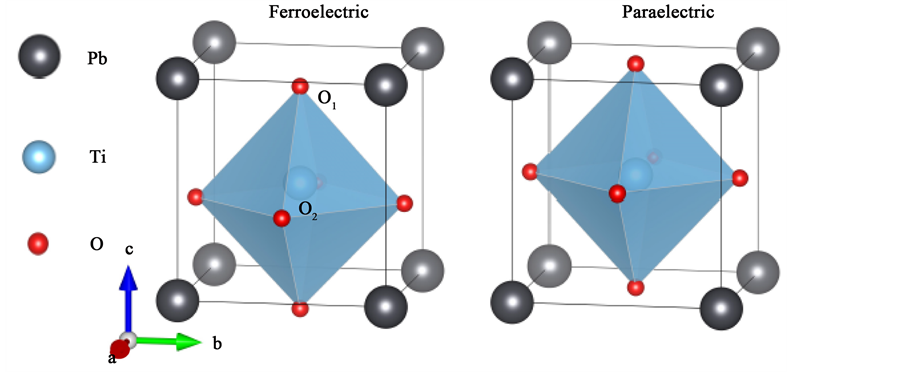
Figure 1. The crystal structure of PbTiO3: the left is ferroelectric phase, the right is paraelectric phase (Pb, Ti, O are located in corner, body center, face center, respectively)
图1. PbTiO3的晶体结构图:左图为铁电相,右图为顺电相(Pb, Ti, O分别位于顶点,体心和面心)
Table 1. The experimental value of PbTiO3 crystal structure
表1. PbTiO3晶体结构实验值
我们在实验的晶体结构 [16] 下利用基于PBE交换关联势的杂化泛函理论,研究长程Hartree-Fork库伦关联项(α)对铁电材料PbTiO3带隙的影响,如图2所示,其中红色虚线为实验值 [17] 。从图中我们发现,计算所得的带隙值随α值的增大而增大,当α为0.325时带隙值与实验值较为接近。图3是此时计算得到的PbTiO3总态密度和分波态密度。我们发现基于PBE交换关联势的杂化泛函理论在带隙计算上的优势非常明显,选用合适的α值,可得到与实验值十分吻合的计算结果。
基于PBE交换关联势的杂化泛函理论我们进一步研究α的选取对晶体结构计算的影响。如表2所示,随着α值的增大,晶格常数a逐渐减小,与实验值差距逐渐拉大,而c逐渐减小,与实验值越来越接近,但仍大于实验值,因此计算得到的c/a的值始终大于实验值。显然利用PBE交换关联势的杂化泛函计算得到的晶体结构与实验值相差较大,因此我们利用PW交换关联势的杂化泛函对PbTiO3的晶体结构进行计算。如表3所示,随着α值的逐渐增大,计算得到的晶格常数a值逐渐减小而c值逐渐增大,c/a的值也因此逐渐增大,当α增加至0.2时,计算得到的c/a的值与实验值比较吻合,其晶体结构数据见表4。另一方面,能带结构计算结果显示,随着α值的逐渐增大,带隙值也逐渐增大。当α = 0.2时,带隙值约为2.46 eV,这远小于实验值。而选取α值0.35时,计算所得的带隙值与实验值较为吻合(3.35 eV),但其晶格常数与实验值相差较大。综上所述,晶体结构和电子结构的计算结果表明杂化泛函对于铁电材料PbTiO3性质的计算的适用性还有待商榷 [18] 。
4. 总结
基于杂化泛函理论,我们考察了长程Hartree-Fork项在交换关联势中所占比例(α)对铁电材料PbTiO3晶体结构和电子结构的影响。我们发现基于PBE交换关联势,当α等于0.325时杂化泛函所得的带隙值与实验结果相吻合。另外,基于PBE和PW交换关联势我们分别研究了α对晶体结构的影响,基于PBE交换关联势的结果与实验值相差较大。而基于PW交换关联势的计算表明,当α等于0.2时的杂化泛函
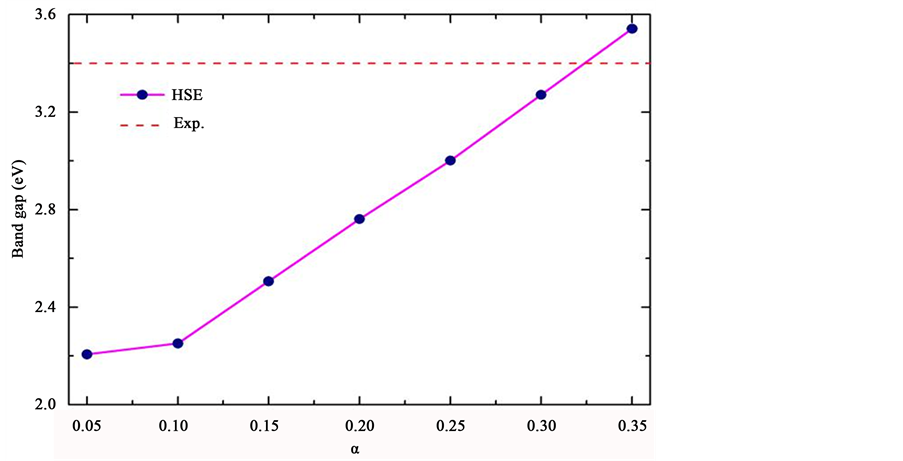
Figure 2. Band gap of PbTiO3 as a function of α. The red dash line is the experimental value
图2. 计算得到的PbTiO3带隙值与Hartree-Fork项(α)的依赖关系,其中红色虚线为实验值 [17]
Table 2. The lattice constants and band gap of PbTiO3 within PBE: a, c, c/a and band gap Egap. The rightmost column in the table is the experimental measurement results
表2. 基于PBE交换关联势杂化泛函方法计算所得PbTiO3的晶格常数a,c,c/a以及带隙Egap。表中最右列是实验测量结果
Table 3. The lattice constants and band gap of PbTiO3 within PW: a, c, c/a and band gap Egap. The rightmost column in the table is the experimental measurement results
表3. 基于PW交换关联势杂化泛函方法计算所得PbTiO3的晶格常数a,c,c/a以及带隙Egap。表中最右列是实验测量结果
表4. 基于PW交换关联势(α = 0.2) PbTiO3的晶体结构值以及与实验结果的比较
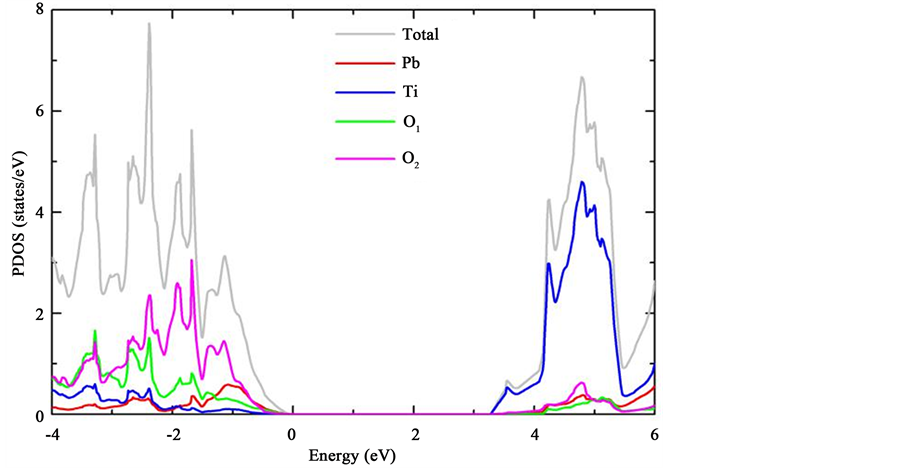
Figure 3. The density of states (DOS) of PbTiO3: The grey line is the total DOS. Red is for Pb. Blue is for Ti. Green and pink is for O1 and O2, respectively
图3. PbTiO3的电子结构态密度:灰色为PbTiO3的总态密度,红色为Pb离子的态密度,蓝色为Ti离子的态密度,绿色和玫红色分别代表O1和O2的态密度
所得的晶体结构与实验结果比较吻合,但此时带隙值却小于实验值。这些结果表明杂化泛函对于铁电材料PbTiO3的适用性还有待商榷 [18] 。
文章引用
王 鹏,周 琚,蔡田怡,雎 胜. 铁电材料PbTiO3晶体结构和电子结构的杂化泛函研究
The Crystal Structure and Electronic Structure of Ferroelectric PbTiO3: A Hybrid Functional Approach[J]. 应用物理, 2017, 07(05): 159-164. http://dx.doi.org/10.12677/APP.2017.75022
参考文献 (References)
- 1. Lines, M.E. and Glass, A.M. (1979) Principles and Applications of Ferroelectrics and Related Materials. OUP Oxford, Ox-ford.
- 2. Ramesh, R. (1997) Thin Film Ferroelectric Materials and Devices. Springer US, New York.
- 3. Scott, J.F. (2000) Ferroelectric Memories. Springer-Verlag, Berlin.
- 4. Kohn, W. and Sham, L.J. (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review, 140, 1133-1138. https://doi.org/10.1103/PhysRev.140.A1133
- 5. Kresse, G. and Hafner, J. (1993) Ab Initio Molecular Dynamics for Liquid Metals. Physical Review B, 47, 558-561. https://doi.org/10.1103/PhysRevB.47.558
- 6. Park, S., Lee, B., Jeon, S.H., et al. (2011) Hybrid Functional Study on Structural and Electronic Properties of Oxides. Current Applied Physics, 11, S337-S340. https://doi.org/10.1016/j.cap.2010.09.008
- 7. Eyert, V. (2011) VO2: A Novel View from Band Theory. Physical Review Letters, 107, Article ID: 016401. https://doi.org/10.1103/physrevlett.107.016401
- 8. Sarmadian, N., Saniz, R., Partoens, B., et al. (2015) Ab Initio Study of Shallow Acceptors in Bixbyite V2O3. Journal of Applied Physics, 117, Article ID: 015703. https://doi.org/10.1063/1.4905316
- 9. Ricardo, G.C. (2012) Why the Heyd-Scuseria-Ernzerh of Hybrid Functional Description of VO2 Phases is Not Correct. Physical Review B, 86, Article ID: 081101. https://doi.org/10.1103/PhysRevB.86.081101
- 10. Iori, F., Gatti, M. and Rubio, A. (2012) Role of Nonlocal Exchange in the Electronic Structure of Correclated Oxides. Physical Review B, 85, Article ID: 115129. https://doi.org/10.1103/PhysRevB.85.115129
- 11. Blochl, P.E. (1994) Projector Augmented-Wave Method. Physical Review B, 50, 17953. https://doi.org/10.1103/PhysRevB.50.17953
- 12. Kresse, G. and Furthmüller, J. (1996) Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Computational Materials Science, 6, 15-50. https://doi.org/10.1016/0927-0256(96)00008-0
- 13. Perdew, J.P., Burke, K. and Ernzerhof, M. (1996) Generalized Gradient Approximation Made Simple. Physical Review Letters, 78, 3865-3868. https://doi.org/10.1103/PhysRevLett.77.3865
- 14. Perdew, J.P. and Wang, Y. (1992) Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Physical Review B Condensed Matter, 45, 13244-13249. https://doi.org/10.1103/PhysRevB.45.13244
- 15. Heyd, J., Scuseriaand, G.E. and Ernzerhof, M. (2003) Hybrid Functionals Based on a Screened Coulomb Potential. Journal of Chemical Physics, 118, 8207-8215. https://doi.org/10.1063/1.1564060
- 16. Kuroiwa, Y., Aoyagi, S., Sawada, A., et al. (2011) Evidence for Pb-O Covalency in Tetragonal PbTiO3. Physical Review Letters, 87, Article ID: 217601. https://doi.org/10.1103/PhysRevLett.87.217601
- 17. Peng, C.H., Chang J.F. and Desu, S. (1992) Ferroelectric Thin Films II.
- 18. Gao, W.W., Abtew, T.A., Cai, T.Y., et al. (2016) On the Applicability of Hybrid Functionals for Predicting Fundamental Properties of Metals. Solid State Communications, 234, 1-50. https://doi.org/10.1016/j.ssc.2016.02.014
