Applied Physics
Vol.07 No.11(2017), Article ID:22828,7
pages
10.12677/APP.2017.711042
Application of Gaussian Surface to the Parameter Extraction of Interconnection Line
Baojun Chen, Yanjie Ju
School of Electrical and Information Engineering, Dalian Jiaotong University, Dalian Liaoning
Received: Nov. 4th, 2017; accepted: Nov. 17th, 2017; published: Nov. 28th, 2017

ABSTRACT
With the further shrinkage of the feature size of integrated circuit, the reliability problem arising from RC delay of interconnection line becomes the main factor affecting the performance of chip. Affected by the manufacturing technology, the cross section of interconnection line is not regular rectangle, and RC delay is thus intensified. The analysis and computation of the parasitic parameter of such interconnection line using numerical method must firstly describe the rough surface. The surface height of interconnection line in the integrated circuit is not easy to measure. To this end, the paper proposes using Gaussian function to describe the rough surface. The experimental data indicate that the application of such surface to the parameters of interconnection line realizes accurate computation result.
Keywords:Gaussian Function, Interconnection Line, Parameter Extraction
高斯表面在互连线参数提取中的应用
陈宝君,鞠艳杰
大连交通大学,电气信息学院,辽宁 大连
收稿日期:2017年11月4日;录用日期:2017年11月17日;发布日期:2017年11月28日

摘 要
随着集成电路特征尺寸的进一步缩小,互连线RC延迟引起的可靠性问题正成为影响芯片性能的主要因素。受制作工艺影响,互连线截面并非规则矩形,而RC延迟问题会因此加剧,采用数值方法分析、计算这种互连线的寄生参数必须首先描述粗糙表面。集成电路中互连线的表面高度并不容易测量,为此,本文提出了使用高斯函数来描述粗糙表面,实验数据表明将该表面应用于互连线参数计算结果较为准确。
关键词 :高斯函数,互连线,参数提取

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着集成电路特征尺寸的进一步缩小,互连线RC延迟和电迁移引起的可靠性问题正成为影响芯片性能的主要因素。金属互连线通常可以选用铜或铝两种材料,由于铜线的低电阻率和高可靠性,目前已经成为互连线的主要材料,被普遍认为是深亚微米和纳米IC多层互连线的首选材料。由于铜不易于干法刻蚀,需采用双嵌入工艺(大马士革工艺)对铜进行布线,其工艺流程可归纳为:刻沟槽→生长阻挡层→铜填充→CMP去除多余的铜和阻挡层。
由于化学等处理方法的影响,实际互连线的表面是粗糙的,如图1所示。有人已经在微尺度下测量了实际导体表面的轮廓,导体表面存在最高和最低之间的距离 [1] [2] [3] 。由于经典电磁理论中趋肤效应的影响,这样的粗糙度会对导线电阻产生显著影响。在高频情况下,当趋肤深度小于最高点和最低点距离的时候,电流集中于导体表面,并且沿着顶点和凹处流动。电流流动的有效长度变大,导体的电阻会有所增加。Tanaka曾经做过实验,实验结果表明由于表面粗糙,不同铜导线的有效电阻值会增加50%到70%。在高速PCB,互连线波导结构以及电子封装中,这样的粗糙表面可以增强导线与绝缘层的粘合度。目前,互连线速度已迅速上升至数G赫兹,表面粗糙度对功耗、信号综合的影响非常明显 [4] [5] [6] 。

Figure1. The surface of interconnect is rough
图1. 互连线表面是粗糙的
2. 生成高斯表面
集成电路中互连线的表面高度并不容易测量,为了得到其高度变化我们可以使用随机粗糙表面模型来进行描述。对于随机表面,需要用一个多变量的概率密度函数来描述其高度。由于高斯函数是稳态,均值为零的,并且统计特性在空间坐标下不变,因此自然界存在的表面通常使用高斯函数来描述。虽然实际的粗糙表面不一定是高斯分布的,但是使用高斯统计可以大大减小这种随机过程的复杂度 [7] [8] [9] 。
设粗糙面上任意一点相对于参考点的高度为 ,它的概率密度函数反映了高度起伏的分布情况,用 表示。知道了高度分布的概率密度函数 ,就可以求出其他的一些统计参量,如高度起伏的均值、均方根等 [10] [11] [12] 。
高度起伏的均值定义为:
(1)
表示沿整个粗糙面求高度的平均值,通常我们都选取适当的参考面,使得相对于此参考面的高度 的均值为零,这会给计算带来很大的方便。
均方根是反映粗糙面粗糙程度的一个基本量,它的最原始定义为:
(2)
与算术平均值相比,均方根值有给大数值加权的效果,即 中大的数值对结果的影响所占成分大。
相关函数也是描述导线表面粗糙程度的重要函数,它表示随机表面上任意两点间的关联程度,定义为:
(3)
进—步定义归一化相关函数,可以得到相关系数:
(4)
我们把相关系数 降至 时的值称为表面相关长度,记为L,即 。表面相关长度是描述随机粗糙面各统计参量中的一个最基本量之一,它提供了估计表面上两点相互独立的一种基准,即如果表面上两点在水平距离上相隔距离大于L,那么该两点的高度值从统计意义上说是近似独立的。
高斯表面生成:蒙特卡洛(Monte Carlo)是用来解决非确定性问题的(概率统计的或随机的)数值方法,也称为统计试验方法 [12] 。随机模拟是蒙特卡洛方法的一种主要应用,可以对实际随机现象进行数值模拟。其生成随机变量序列的基本思想为:根据欲研究对象的性质,建立能够描述其特性的理论模型,导出该模型的某些特征量的概率密度函数;从概率密度函数出发进行随机抽样,得到特征量的一些模拟结果;对模拟结果进行分析总结,预言物理系统的某些特性。
对于任意概率分布的模拟方法为:若随机变量X的概率分布函数为 ,根据概率分布函数的性质有 ,为了得到具有概率分布函数 的随机数X,我们可以通过产生 内均匀分布随机数U,经转换可得到服从 分布的随机样本X。具体方法如下:
设 ,即可得:
(5)
式中,随机变量U在 内服从均匀分布,X具有分布函数 。
由于高斯分布的积分无法用简单的函数来表示,完成逆映射比较困难,所以上述先产生均匀随机变量再求反函数的方法无法得到高斯分布,因此需要使用其他方法。由随机过程理论可知:一对统计独立的高斯随机变量和与一个服从瑞利分布的随机变量满足如下关系式:
, (6)
式中,随机变U,V服从高斯分布,随机变量X服从瑞利分布,随机变量 服从 内的均匀分布。显然容易求出随机变量X和随机变量 ,利用公式(6)可以求得两个独立的高斯分布随机变量。
服从瑞利分布的随机变量其分布函数为:
(7)
由上述分析可知为了得到具有瑞利分布函数 的随机数X,同样可通过产生 内均匀分布随机数W,经转换得到服从瑞利分布的随机样本X。
设 ,即可得
(8)
式中,随机变量W在 内服从均匀分布,则X具有瑞利分布函数。
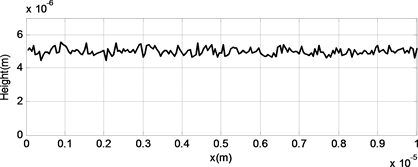
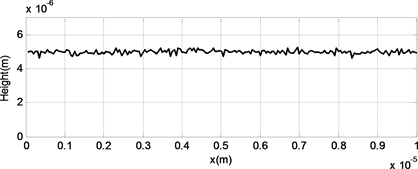
图2为使用上述方法生成的高度服从高斯分布的随机表面,导线的宽度为10微米,厚度为5微米。三个图中的均方根参数不同。均方根是描述表面粗糙程度的重要参数,值的大小反映了表面的粗糙程度。从图中可以看出,均方根值越大,表示导线越粗糙,表面高度值波动越大。
粗糙表面导线的高度生成后,需要对导体截面进行混合网格划分。为了简化网格划分并且尽量减少网格数量,只对导体表面粗糙的部分使用三角形和矩形的混合划分,形状规则的导体部分仍然使用矩形网格。
3. 粗糙表面参数计算结果
为了验证本文算法的正确性,将计算结果与文献 [13] 的结果对比,文献中没有直接计算粗糙表面导体的电阻,而是计算了导线的有效电导率偏差,有效电导率偏差的计算公式为:
(9)
图3为计算结果对比图,RMS值为1微米。从图中结果可以看出,本文方法计算结果与文献结果吻合较好。图4为相同相关长度值,均方根值不同时粗糙表面导线电阻值与光滑表面电阻值的比较,为了说明粗糙表面对导线电阻参数的影响,图中给出了不同频率下粗糙表面导线电阻值与光滑表面电阻值的比值。从图中可以看出,电阻比值均大于1,说明粗糙表面的存在导致导线电阻增加,并且随着频率的升高比值在不断增加。当均方根值为0.01微米时,比值最大为1.014而均方根值为1微米时,比值的最大值达到了1.56,因而从数值结果可以证明导线的表面越粗糙,对互连线电阻参数的影响越大。
除了均方根之外,相关长度也是影响粗糙度的一个重要参量,相关长度越小,表面越粗糙,相反表示表面光滑。图5给出了在均方根相同,相关长度不同时的电阻比值。由图可以看出,相关长度越小,电阻值的比值越大。
根据上面分析可知,粗糙表面对互连线电阻的影响较大,因此对粗糙表面导线电阻的计算由为重要。
 (a)
(a)
 (b)
(b)
 (c)
(c)
Figure 2. Gaussian rough surface (a) RMS = 0.5 um, (b) RMS = 0.2 um, (c) RMS = 0.1 um
图2. 高斯表面(a) RMS = 0.5 um,(b) RMS = 0.2 um,(c) RMS = 0.1 um
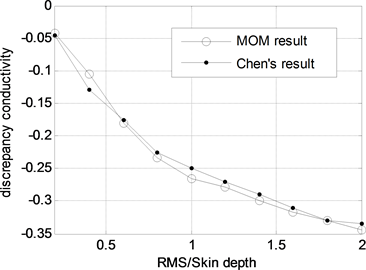
Figure 3. Corresponding discrepancy between mean effective conductivity and normal conductivity
图3. 表面粗糙导线的有效电导率与表面光滑导线电导率比较图
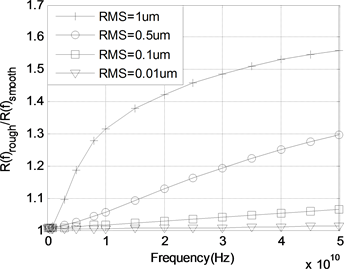
Figure 4. Resistance ratio as a function of frequency
图4. 电阻比值随频率变化图
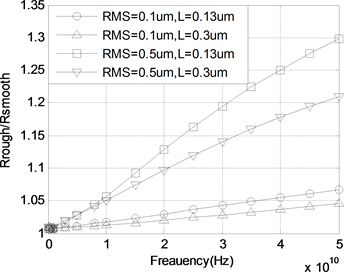
Figure 5. Resistance ratio as a function of frequency
图5. 电阻比值随频率变化图
4. 结论
受制作工艺影响,实际互连线截面并非是光滑的。为了使互连线参数提取结果更加接近实际情况,本文对互连线粗糙表面进行了描述。本文使用高斯函数来模拟粗糙表面,使用均方根,相关函数等参数来区别粗糙度不同的表面,通过对结果的分析,验证了该方法的正确性。
文章引用
陈宝君,鞠艳杰. 高斯表面在互连线参数提取中的应用
Application of Gaussian Surface to the Parameter Extraction of Interconnection Line[J]. 应用物理, 2017, 07(11): 344-350. http://dx.doi.org/10.12677/APP.2017.711042
参考文献 (References)
- 1. Wu, Z. and Davis, L.E. (1994) Surface Roughness Effect on Surface of Impedance of Superconductors. Journal of Applied Physics, 76, 3669-3672. https://doi.org/10.1063/1.357430
- 2. Biot, M.A. (1957) Some New Aspects of the Reflection of Electromagnetic Waves on a Rough Surface. Journal of Applied Physics, 28, 1455-1463. https://doi.org/10.1063/1.1722676
- 3. Wait, J.R. (1959) Guiding of Electromagnetic Waves by Uniformly Rough Surface-Part 1. Antennas and Propagation, 7, 154-162. https://doi.org/10.1109/TAP.1959.1144764
- 4. Zhu, Z.H., Demir, A. and White, J.B. (2004) A Stochastic Integral Equation Method for Modeling the Rough Surface Effect On Interconnect Capacitance. Computer Aided Design, 887-891.
- 5. Wilton, D., Rao, S. and Glisson, A. (1984) Potential Integrals for Uniform and Linear Source Distributions on Polygonal and Polyhedral Domains. IEEE Transactions on Antennas and Propagation, 32, 276-281. https://doi.org/10.1109/TAP.1984.1143304
- 6. Gralia, R.D. (1993) On the Numerical Integration of the Linear Shape Functions Times the 3-D Greens Function or Its Gradient on a Place Triangle. IEEE Transactions on Antennas and Propagation, 41, 1448-1455. https://doi.org/10.1109/8.247786
- 7. Morgan, S.P. and Samuel, P. (1949) Effect of Surface Roughness on Eddy Current Losses at Microwave Frequencies. Applied Physics, 20, 352-362. https://doi.org/10.1063/1.1698368
- 8. 盛新庆. 计算电磁学要论[M]. 北京: 科学出版社, 2004.
- 9. Duffy, M.G. (1982) Quadrature over a Pyramid or Cube of Integrands with a Singularity at a Vertex. SIAM Journal on Numerical Analysis, 19, 1260-1262. https://doi.org/10.1137/0719090
- 10. 王浩刚, 聂在平. 三维矢量散射积分方程中奇异性分析[J]. 电子学报, 1999, 27(12): 68-71.
- 11. Geoffrey, R.G. and David, R.S. (2001) Probability and Random Processes. Oxford University Press, Oxford.
- 12. Tsang, L., Kong, J.A. (2001) Electromagnetic Waves: Numerical Simulations. John Wiley and Sins, New York. https://doi.org/10.1002/0471224308
- 13. Chen, Q. and Wong, N. (2008) Efficient Numerical Modeling of Random Rough Surface Effects for Interconnect Internal Impedance Extraction. Design Automation Conference.