Computer Science and Application
Vol.3 No.4(2013), Article ID:12107,3 pages DOI:10.12677/CSA.2013.34039
The Extension of the Rough Set Model*
1Department of Science, Wuhan University of Technology, Wuhan
2Department of Computer Science, Wuhan University of Technology, Wuhan
Email: 578067715@qq.com
Received: Apr. 28th, 2013; revised: May 16th, 2013; accepted: May 28th, 2013
Copyright © 2013 Mengjie Wang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT:
Because of the incomplete information and inequivalent binary relation on the domain, the classic rough set model will need to be expanded. On the one hand, the equivalence relations of the rough set model is extended to tolerance relations or inclusion relations, which can extend the application range. This paper studies high and low approximation operators on the basis of this method and compares with the two kinds of relations through case analysis. On the other hand, on the basic of granularity of knowledge structure and knowledge representation method, it studies the approximation operators from two aspects of neighborhood system and granularity.
Keywords: The Rough Set Model; Tolerance Relations; Contains Relations; Approximation Operators; Neighborhood Systems
粗糙集模型的拓广*
王梦洁1,许爱琴1,刘永坚2,王卫华1
1武汉理工大学理学院,武汉
2武汉理工大学计算机学院,武汉
Email: 578067715@qq.com
摘 要:
由于信息的不完备以及论域上的二元关系常常是不等价的,需要将经典粗糙集模型进行扩充。一方面,将粗糙集模型中等价关系泛化为容差关系或包含关系,可将粗糙集模型的适用范围扩大,在此基础上研究其上、下近似算子,并通过案例对比两种关系的差别;另一方面,从基本知识粒度的构造和知识的表示方法上,研究基于邻域系统和粒度两个方面的上、下近似算子。
收稿日期:2013年4月28日;修回日期:2013年5月16日;录用日期:2013年5月28日
关键词:容差关系;包含关系;粗糙集模型;近似算子;邻域系统
1. 引言
粗糙集模型是一种新型的数学工具,主要适用于处理不精确、模糊和不完备性问题。在认知科学和人工智能方面尤为重要,同时也是粒度计算研究的重要方向。该理论模型已经在机器学习与知识发现、数据挖掘、决策支持与分析等方面得到广泛应用。目前,有3个有关粗糙集的系列国际会议,即RSCTC、RSFDGrC和RSKT。中国学者在这方面也取得了很大的成果。从2001年开始每年召开中国粗糙集与软计算学术会议:RSFDGRC2003、IEEEGrC2005、RSKT 2006、IFKT2008、RSKT2008、IEEE GrC2008等一系列国际学术会议在中国召开[2]。
但它同时也存在着一定的问题,例如,缺乏有效的代数运算体系来处理现实问题;过于依赖论域上的关系来表示知识;描述粒度间结构信息的方法过少;对基本粒度的缺少语义解释等。基于上述原因,需要将粗糙集模型进行改进。粗糙集模型的核心基础是从近似空间导出一对近似算子经典Pawlak模型中的不分明关系是一种等价关系,要求很高。因此,如何推广定义近似算子成为了改进粗糙集模型的一个重点。
2. Pawlak的粗糙集模型
给定论域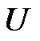 为有限非空集合且存在等价关系
为有限非空集合且存在等价关系 :
: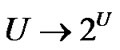 ,则称序对
,则称序对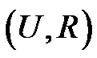 是一个近似空间或知识库。令
是一个近似空间或知识库。令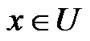 ,Pawlak定义由等价关系确定的等价类
,Pawlak定义由等价关系确定的等价类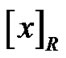 的集合组成
的集合组成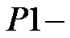 粗糙集集合
粗糙集集合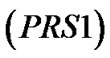 。
。
定义1[2] 设论域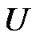 上的等价关系
上的等价关系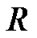 ,
, ,上、下近似算子
,上、下近似算子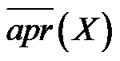 、
、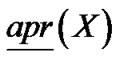 定义为:
定义为:


借助对上下近似算子的描述,可以了给出和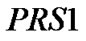 等价的另外一种关于粗糙集的定义,称为
等价的另外一种关于粗糙集的定义,称为 粗糙集集合。即
粗糙集集合。即
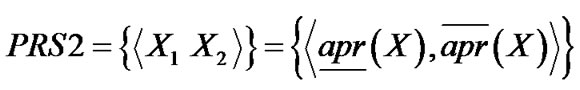 。
。
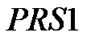 和
和 统称为Pawlak粗糙集。
统称为Pawlak粗糙集。
但在许多实际问题中,由于信息的不完备以及论域上的二元关系往往是不等价的,导致基本粒度的运算不一定封闭,且代数系统尚不完善,这些因素使得Pawlak经典粗糙集模型的应用受到限制,为此必须将它改进。
3. 等价关系的泛化
可以将等价关系泛化为容差关系、量化容差关系、包含关系、模糊关系等等,下面仅对容差关系和包含关系进行研究。
3.1. 容差关系
由Kryszkiewicz提出的容差关系的关键在于将不完备信息表中没有值的对象赋予一个 值。这个
值。这个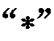 值有可能是任何值。且这个值是确实存在但被遗漏掉的,也就是说每个对象都具有实际存在但被遗漏的属性信息。如果给定信息表
值有可能是任何值。且这个值是确实存在但被遗漏掉的,也就是说每个对象都具有实际存在但被遗漏的属性信息。如果给定信息表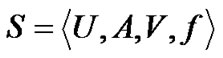 ,其中
,其中 ,
,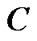 是条件属性集合,
是条件属性集合, 是决策属性。对于具有遗漏属性值的属性子集
是决策属性。对于具有遗漏属性值的属性子集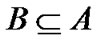 ,Kryszkiewicz定义了如下的容差关系
,Kryszkiewicz定义了如下的容差关系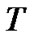 [4]。
[4]。
定义2[4] 容差关系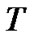 的定义:
的定义:
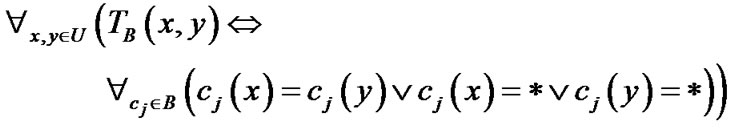
由定义可以看出: 满足自反性和对称性,但不一定是传递的。将具有遗漏属性值的属性集
满足自反性和对称性,但不一定是传递的。将具有遗漏属性值的属性集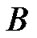 上满足关系
上满足关系 的对象
的对象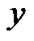 的集合用符号
的集合用符号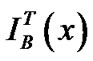 表示,称为对象
表示,称为对象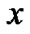 的容差类。
的容差类。
基于容差类的定义,Kryszkiewicz同时也定义了对象集合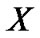 关于属性集
关于属性集 上的上近似和下近似。
上的上近似和下近似。
定义3[4] 完备信息表 中对象集合
中对象集合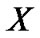 关于属性集
关于属性集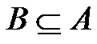 的上近似
的上近似 和下近似
和下近似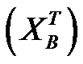 分别为
分别为
 ,
,
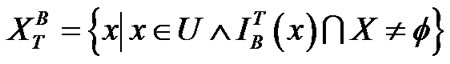 。
。
显然,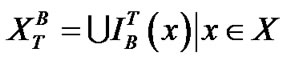 。
。
3.2. 包含关系
事实上,由于对象本身不能被所提供的属性来描述同样可以导致个体对象的属性信息不完整,因此,上节所说的未知值还可能是不存在的,无法进行比较。这个时候,只要某对象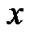 的已描述属性与另一对象
的已描述属性与另一对象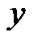 对应相同,就认为个体对象
对应相同,就认为个体对象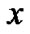 包含于对象
包含于对象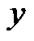 中。同样记未知值为“*”,对于给定信息表
中。同样记未知值为“*”,对于给定信息表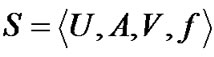 ,其中,
,其中,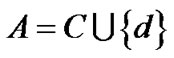 ,
,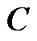 是条件属性集合,属性子集
是条件属性集合,属性子集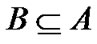 ,令
,令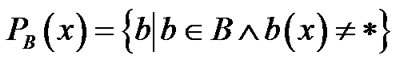 。
。
定义4 将包含关系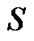 定义为:
定义为:
 。
。
包含关系 显然不满足对称性,但具有传递性和自反性,且是对象集合
显然不满足对称性,但具有传递性和自反性,且是对象集合 上的偏序。
上的偏序。
定义5 包含于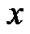 的对象集合
的对象集合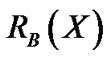 ,包含
,包含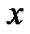 的对象集合
的对象集合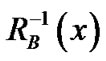 定义为:
定义为:
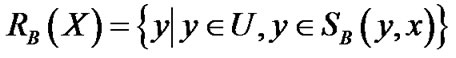 ,
,
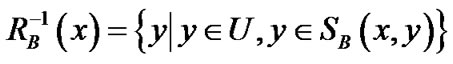 。
。
定义6 将给定不完备信息表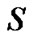 中对象集
中对象集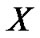 关于属性集
关于属性集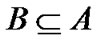 的上近似
的上近似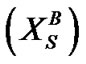 和下近似
和下近似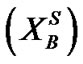 定义为
定义为
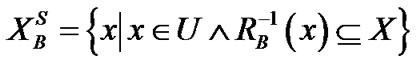 ,
,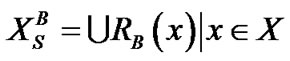 。
。
也就是说,如果 中的某个对象包含对象
中的某个对象包含对象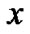 ,则对象
,则对象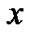 有可能属于
有可能属于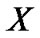 类;反之,如果对象
类;反之,如果对象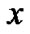 与包含它的对象都包含于
与包含它的对象都包含于 ,则对象
,则对象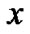 肯定属于
肯定属于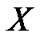 类。
类。
3.3. 案例分析
下面用一个实际的不完备信息表来分析比较这两种扩充方法。
对于如表1所示的信息表,其中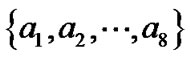 表示对象集合,
表示对象集合,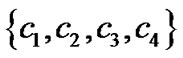 表示条件属性集合,值域均为[0,1,2,3],“*”代表未知值,决策属性
表示条件属性集合,值域均为[0,1,2,3],“*”代表未知值,决策属性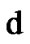 将对象集分为
将对象集分为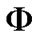 和
和 两个集合。
两个集合。
首先用容差关系来分析这个信息表,得:
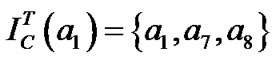 ,
,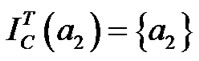 ,
,
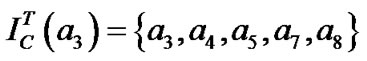 ,
,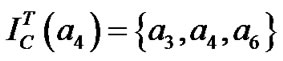
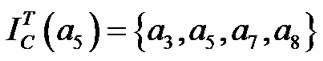 ,
,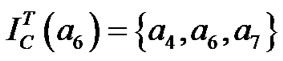 ,
,
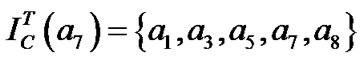 ,
, ,
,
 ,
, ,
,
 ,
,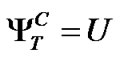 。
。
从分析得到的结果看,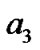 和
和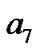 是近似相同的。但是从信息表的内容看,这两个对象没有一个相同的属性值,只是有可能相同,而且可能性不大。
是近似相同的。但是从信息表的内容看,这两个对象没有一个相同的属性值,只是有可能相同,而且可能性不大。
对于表1用包含关系来分析,得到如下计算结果:
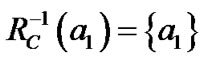 ,
,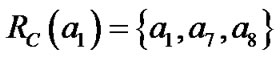 ,
,
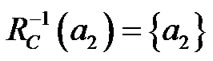 ,
,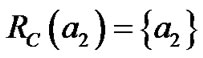 ,
,

Table 1. An incomplete information table
表1. 一个不完备信息表
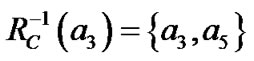 ,
,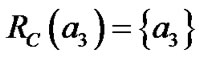 ,
,
 ,
, ,
,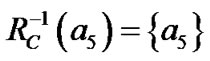 ,
,
 ,
,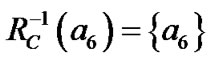 ,
,
 ,
,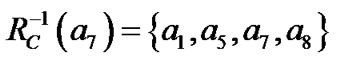 ,
,
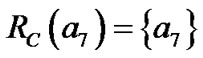 ,
, ,
,
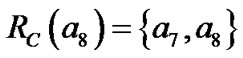 ,
,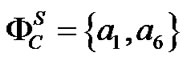 ,
,
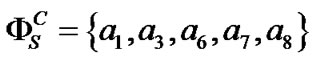 ,
, ,
,
 。
。
从结果上看,根据包含关系得到的近似集所含的信息更多。而且,从信息表直接看来希望分类到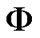 和
和 的元素通过计算也分别包括在
的元素通过计算也分别包括在 和
和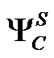 中。
中。
4. 基本知识粒度的构造和知识的表示方法 的拓广
4.1. 基于粒度的上、下近似算子
在近似空间中,论域 被等价关系
被等价关系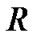 划分为两两互不相交的等价类的并,即
划分为两两互不相交的等价类的并,即 ,称商集
,称商集
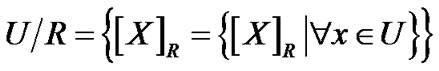 是近似空间的一组知识基,同时也代表了论域的一种粒度[1]。
是近似空间的一组知识基,同时也代表了论域的一种粒度[1]。
为了保证运算的封闭性,需要将粗糙集的商集拓广成一个拓扑空间,用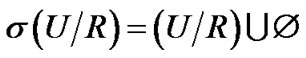 (
( 满足对交、并运算封闭)替换商集
满足对交、并运算封闭)替换商集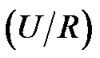 ,它是一个
,它是一个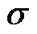 代数,且
代数,且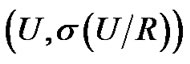 构成了一个拓扑空间,也是布尔代数
构成了一个拓扑空间,也是布尔代数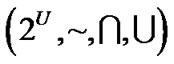 的一个子代数。则基于粒度的下、上近似分别可表示为[5]:
的一个子代数。则基于粒度的下、上近似分别可表示为[5]:
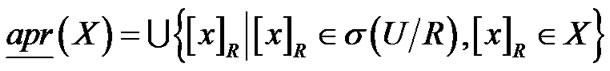 ;
;
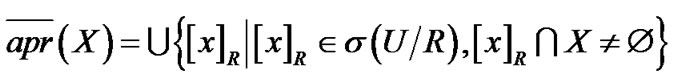 。
。
4.2. 基于邻域系统的上、下近似算子
4.2.1. 邻域系统
引理1[6] 关系粒计算的定义。令
1)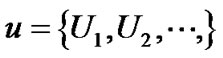 为一族论域的集合;
为一族论域的集合;
2)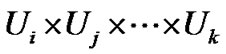 为
为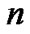 个论域上的笛卡尔积,其中
个论域上的笛卡尔积,其中 ;
;
3)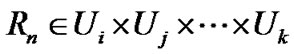 称为一个
称为一个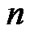 元关系;
元关系;
4)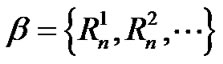 是一族等价关系的合集;称二元组
是一族等价关系的合集;称二元组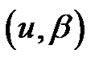 为关系粒计算模型。
为关系粒计算模型。
在关系粒计算模型中,如果令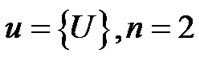 ,即只考虑一个论域,此时的关系粒计算模型就退化为二元粒计算模型。由此可见,二元粒计算模型则是关系粒计算模型的一种特殊情形,而关系粒计算模型是二元粒计算模型的广义表示形式。
,即只考虑一个论域,此时的关系粒计算模型就退化为二元粒计算模型。由此可见,二元粒计算模型则是关系粒计算模型的一种特殊情形,而关系粒计算模型是二元粒计算模型的广义表示形式。
引理2[6] 在二元粒计算模型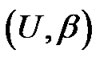 中,
中,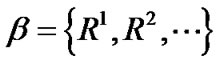 ,则对于
,则对于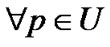 ,有一族子集与之对应,即:
,有一族子集与之对应,即:
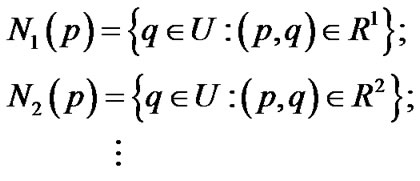 ;
;
1)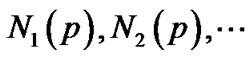 称为
称为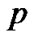 的邻域;
的邻域;
2) 的所有邻域的合集称为
的所有邻域的合集称为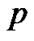 的领域系统,记为
的领域系统,记为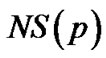 ,即
,即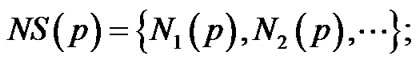
3) 集合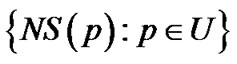 称为
称为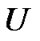 的邻域系统,记为
的邻域系统,记为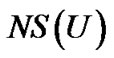 。
。
4.2.2. 近似算子
经典粗糙集模型论域 中的每一个对象有且只有一个对应的等价类,若这个等价类看作此对象的邻域,就可以构成此对象的邻域系统,由此可定义基于邻域系统的近似算子。
中的每一个对象有且只有一个对应的等价类,若这个等价类看作此对象的邻域,就可以构成此对象的邻域系统,由此可定义基于邻域系统的近似算子。
定义7 在拓扑空间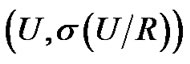 中,对
中,对 的下、上近似算子定义如下:
的下、上近似算子定义如下:


与经典粗糙集模型不同,基于邻域的粗糙集模型中,以下关系不成立[6]:
1) ;
;
2)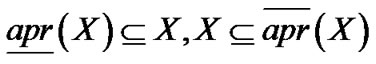 ;
;
3) 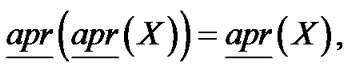
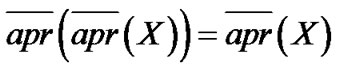 ;
;
虽然上下近似的各种表示方法不尽相同,但本质都是从幂集到幂集的映射,由此得到一个粗糙集代数
系统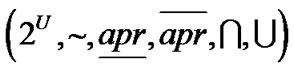 。
。
4.2.3. 案例分析
令论域 ,
,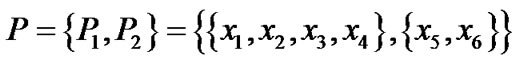 为论域上根据等价关系
为论域上根据等价关系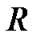 得到的划分,若
得到的划分,若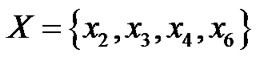 ,根据定义,得到如下所示邻域系统:
,根据定义,得到如下所示邻域系统:

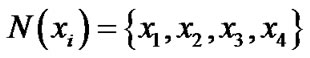
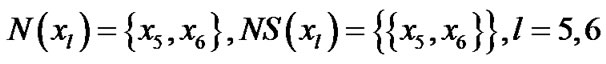
由此得到基于邻域系统的粗糙集为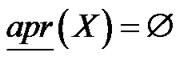 ,
,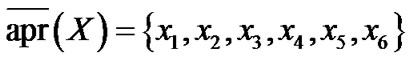 。
。
5. 结论
笔者从两个方面对粗糙集模型进行拓广,提供了有效处理信息的途径,他让粗糙集理论与其他理论可以有效衔接。 定义的经典粗糙集模型适用于逻辑推理,基于邻域的定义可用于处理具有拓扑性质的信息,基于粒度的定义则可以更好的适用于粒度计算。
定义的经典粗糙集模型适用于逻辑推理,基于邻域的定义可用于处理具有拓扑性质的信息,基于粒度的定义则可以更好的适用于粒度计算。
参考文献 (References)
[1] 李道国, 苗夺谦, 张东星, 张红云. 粒度计算研究综述[J]. 计算机科学, 2005, 32(9): 3-6.
[2] 王国胤, 姚一豫, 于洪. 粗糙集理论与应用研究综述[J]. 计算机学报, 2009, 32(7): 1231-1237.
[3] 顾力平,杨习贝. 基于一般二元关系的多粒度粗糙集模型[J].南京航空航天大学学报, 2013, 45(1): 125-128.
[4] 马周明, 李进金. 基于强对称关系的广义粗糙集模型[J]. 模式识别与人工智能, 2012, 25(4): 558-563.
[5] 代春艳. 粗糙集理论及其应用发展综述[J]. 重庆工商大学学报, 2004, 21(6): 575-579.
[6] 杨习贝, 杨静宇. 邻域系统粗糙集模型[J]. 南京理工大学学报, 2012, 36(2): 292-293.
[7] Y. H. Qian, J. Y. Liang and W. Wei. Pessimistic rough decision. Second International Workshop on Rough Sets Theory. Zhoushan, 19-21 October 2010, 440-449.
[8] R. Slowinskn, D. Vanderpooten. A generalized definition of rough approximations. ICS Research Report, 1996.
NOTES
*资助项目:科技部“十二五”国家科技支撑计划课题“文化遗产知识本体构建存储可视化技术研究”(2012BAH33F03)。