Computer Science and Application
Vol.07 No.08(2017), Article ID:21681,21
pages
10.12677/CSA.2017.78087
A Novel Image Encryption Algorithm Based on Improved Standard Mapping
Yucheng Chen, Ruisong Ye
Department of Mathematics, Shantou University, Shantou Guangdong

Received: Jul. 24th, 2017; accepted: Aug. 6th, 2017; published: Aug. 14th, 2017

ABSTRACT
This paper proposes an image encryption algorithm based on improved standard mapping. The standard mapping is improved by introducing the nonlinear term of the variables and the linear combination of the parameters. The phase space diagram, Lyapunov exponent and time series tests of the improved standard mapping show that improved standard mapping has good random performance. A new gray image encryption algorithm is then designed using the improved standard mapping. In the permutation stage, the improved standard map is applied to disorder the pixels positions to achieve good scrambling effect. In the diffusion stage, the mechanism of dynamic feedback is used to make the diffusion process have fair diffusion and encryption effect. Finally, the performance analysis is carried out, including key space analysis, key sensitivity analysis, statistical analysis, etc. Simulation experiments show that the encryption algorithm proposed has a large key space, strong key sensitivity, strong robustness against statistical analysis attack, brute force attack, differential analysis attack, and chosen\known plaintext attacks, etc.
Keywords:Standard Mapping, Chaos, Image Encryption
基于改进标准映射的图像加密算法
陈裕城,叶瑞松
汕头大学数学系,广东 汕头
收稿日期:2017年7月24日;录用日期:2017年8月6日;发布日期:2017年8月14日

摘 要
本文提出一种基于改进标准映射的图像加密算法。首先,针对标准映射用于图像置乱加密时的密钥空间小等不足,通过引进变量的非线性项和含参量的线性组合对标准映射进行改进。改进标准映射的相位空间图、Lyapunov指数、时间序列测试均表明了改进标准映射具有良好的随机性能。同时,利用改进标准映射设计了一种新的灰度图像加密算法,在置换阶段,采用改进的标准映射实现置乱得到较好的置乱效果;在扩散阶段,采用动态反馈方式的机制使得扩散过程有很好的扩散加密效果。最后,本文还提出了与本文灰度图像加密算法相关的性能分析,包括密钥空间分析、密钥敏感性分析、统计分析等,所有的仿真实验均表明,本文提出的加密算法对各种已知攻击具有非常强的鲁棒性,并且具有密钥空间大、密钥敏感性强、可抵抗统计分析攻击、蛮力攻击、差分攻击、已知明文和选择明文攻击等优良特性。
关键词 :标准映射,混沌,图像加密

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
进入21世纪以来,随着网络通信技术和多媒体技术的快速发展,人们的生活方式发生了天翻地覆的变化,从古时候只能通过书信来交流各种各样的重要信息到现在只需按下发送键就可以轻松地与他人交流。知乎等新兴社交媒体的出现,更是极大地丰富了我们学习知识和交流思想的方式。与此同时,也隐含了许许多多的信息安全隐患,一些不法分子通过恶意攻击等手段获取我们的个人敏感信息来做违法的事情。近几年来,无论国际还是国内报道的有关信息泄漏或被非法窃取的事件是多如牛毛,比如美国‘棱镜门’事件 [1] ,华为公司内部信息泄漏 [2] 等等。这些时常发生的事件更是提醒我们要对信息安全问题提高警惕。信息的载体如文字、图像、视频等在公共网络上的传输是造成信息泄露的一个重要原因,而图像因其直观性强、可识别性高等特点占据了我们日常信息交流载体的很大一部分,因此,对图像进行保护就显得非常重要。现阶段图像保护主要有两个方法,一个是通过嵌入数字水印等方法来保护图像的版权;另外一个是通过某种变换或映射对明文图像的特征信息进行隐藏,即图像加密。前者在网络传输过程中图像的一些明显特征不会改变,只是增加了易于识别的水印信息,而后者则相反,即希望通过变换把原图像一些重要的特征隐藏起来。所以,在我们现实生活中,图像加密是对图像进行保护的重要手段。图像由于自身的一些内在特点如数据量大、数据冗余度高和相邻像素相关性强等使得大部分的传统文本加密经典算法如DES(Data Encryption Standard),AES(Advanced Encryption Standard)等不再适用于图像加密 [3] 。因此,研究者们提出了大量不同于传统文本加密的算法去对图像进行加密 [4] 。在这些算法中,基于混沌理论的加密算法引起了人们极大的关注。
混沌,大自然中具有确定性规律的伪随机状态的描述,是指发生在确定性系统中貌似随机的不规则运动 [5] 。就是说,一个用确定性理论描述的系统,其行为却表现为不确定、不可重复和不可预测等。混沌系统具有对系统初值和参数的极端敏感性、伪随机性、状态遍历性等的混沌特性 [6] 。正是因为这些性质与密码学中的典型要求非常契合,如混沌对参数和初值的敏感性与加密系统对密钥极端敏感之间的对应、混沌的拓扑传递性和混合特性与加密系统的扩散之间的对应等 [7] ,所以利用混沌系统来设计对图像加密算法具有很好的应用前景。
自从1989年英国学者Matthews将混沌理论引入图像加密的研究中 [8] ,就有大批的学者涌入基于混沌的图像加密研究中。1998年,Fridrich利用二维混沌系统提出基于置乱–扩散结构的图像加密算法 [9] 。在置乱过程中,首先利用二维混沌系统对明文图像像素的位置进行置乱,然后在扩散操作中利用一维混沌映射产生的伪随机序列来加密扩散置乱后的像素。基于置乱–扩散结构的算法占据现有图像加密算法的很大部分 [4] - [24] 。其中,在文献 [12] 中,应用离散混沌动力系统设计了一种具有SP (Substitution-Permutation)结构的图像加密算法。该算法在置乱阶段采用类标准映射产生随机数对明文图像进行位置置乱,通过引入两个1维混沌映射,巧妙地构造出具有强耦合结构的类标准映射,并由其产生伪随机序列对明文图像进行像素位置的置乱,并且该置乱算法的置乱效果比用原标准映射置乱的效果要好。在扩散阶段则采用另外的1维映射产生随机数,利用取模的方式对置乱后的图像像素进行扩散。该算法充分利用 维混沌映射对图像加密,密钥空间大,易于软件实现。文献 [4] 构造了一个新的二维耦合混沌系统,提出了基于新耦合系统的快速图像加密算法。这个算法对图像像素的置乱和扩散同时执行,减少了整个加密过程的时间消耗。首先,提出基于混沌系统的一个混沌位移(CST, Chaotic shift transform)置乱算法,同时把行列代替运用到置乱后的像素值中。这种方法由于像素置乱和扩散同时执行而大大地减少了执行时间,新构造的二维耦合混沌映射具有很好的混沌特性,使得整个算法有不错的加密效果。在文献 [13] 中,提出一种块图像置乱算法和基于动力指数的扩散机制。首先把明文图像在水平方向或者垂直方向分成2个相等子块图,然后利用Logistic混沌系统产生2个与图像子块相同大小的坐标索引值矩阵、1个控制两个图像子块交换的控制变换矩阵,进而利用三个矩阵对分块后的两幅图像进行它们之间的像素交换,即对图像的像素位置进行置换产生两幅置乱图,最后采用按位异或运算和取模运算对合并后的置乱图进行像素扩散。这一算法巧妙地构造控制交换矩阵和基于反馈像素的扩散方法使得整个加密算法具有强鲁棒性。文献 [14] 提出一种基于Chirikov混沌系统、离散小波变换(DWT, Discrete Wavelet Transform)和多级树集合分裂(SPIHT, Set Partitioning in Hierarchical Trees)的图像压缩加密算法。算法采用Chirikov标准映射作为混沌系统对明文图像进行置乱,用包含压缩、扩散的变换对置乱后的图像进行加密。这个算法将信号处理领域的时频分析引入到图像加密中来,丰富了图像加密算法的设计思路。
文献 [15] 提出一种改进扩散策略来改善众多现有基于置乱–扩散机制图像加密算法的加密效果。用离散化的标准映射对明文图像像素的位置进行置乱操作,用新的双向扩散策略对图像进行扩散,即在一般流加密的基础上,增加了反方向的像素扩散,但在置乱过程中,离散标准映射的参数只有一个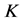 ,即置乱阶段的参数空间由
,即置乱阶段的参数空间由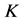 组成,而且计算简单,从密码学角度来说,可用作密钥的参数少,即密钥空间比较小,用此系统产生的伪随机序列非常容易被预测,当参数
组成,而且计算简单,从密码学角度来说,可用作密钥的参数少,即密钥空间比较小,用此系统产生的伪随机序列非常容易被预测,当参数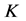 取为定值时,一幅明文图像经过3次置乱后,置乱后的图像仍出现条纹状,这些对于一个安全的加密算法来说,无疑是个安全隐患,在扩散阶段,虽然从正向和反向两个方向扩散能加快像素的扩散速度,但统计分析效果不佳。所以,本文对标准映射进行了探讨,对其改进并将利用改进后的标准映射设计图像加密算法。首先分析标准映射的特性,然后通过增加含参数的线性组合项和变量的非线性项对标准映射进行改进,分析其混沌动力学行为如空间相位图、Lyapunov指数等的特性。最后采用改进的标准映射来设计灰度图像加密算法。利用改进的标准映射来设计算法,可以增大密钥空间和加速混沌行为的发生,在扩散阶段,采用动态反馈机制对置乱后的图像像素灰度值进行扩散。
取为定值时,一幅明文图像经过3次置乱后,置乱后的图像仍出现条纹状,这些对于一个安全的加密算法来说,无疑是个安全隐患,在扩散阶段,虽然从正向和反向两个方向扩散能加快像素的扩散速度,但统计分析效果不佳。所以,本文对标准映射进行了探讨,对其改进并将利用改进后的标准映射设计图像加密算法。首先分析标准映射的特性,然后通过增加含参数的线性组合项和变量的非线性项对标准映射进行改进,分析其混沌动力学行为如空间相位图、Lyapunov指数等的特性。最后采用改进的标准映射来设计灰度图像加密算法。利用改进的标准映射来设计算法,可以增大密钥空间和加速混沌行为的发生,在扩散阶段,采用动态反馈机制对置乱后的图像像素灰度值进行扩散。
本文的结构如下,在第1节我们简单地介绍标准映射及其改进,首先,通过标准映射的空间相位图等探讨一些动力学性质,然后对标准映射进行改进并分析其动力学性质,最后比较标准映射和改进标准映射在图像置乱的效果;第2节提出基于改进标准映射的灰度图像加密算法;提出加密算法的仿真实验和加密性能分析放在第3节,最后在第4节给出本文总结。
2. 标准映射及其改进
2.1. 标准映射
在混沌动力学理论中,有一类映射称为标准映射,又称Chirikov标准映射,它是一种从边长为 的正方形区域到它自己的保面积映射。其数学公式定义如下 [9] :
的正方形区域到它自己的保面积映射。其数学公式定义如下 [9] :
 (1)
(1)
这里 是满足大于0的系统控制参数,
是满足大于0的系统控制参数,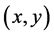 位于
位于 方形区域。
方形区域。
标准映射是对称的并且退化能产生某些特殊的特性,如当参数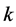 逐渐减小时,其混沌轨道会较快出现“岛礁”形状。标准映射的雅可比矩阵的行列式值为1,因而是二维保面积映射,而且有两个不动点:
逐渐减小时,其混沌轨道会较快出现“岛礁”形状。标准映射的雅可比矩阵的行列式值为1,因而是二维保面积映射,而且有两个不动点: ,
, 。标准映射的参数
。标准映射的参数 对系统(1)的混沌动力学行为起着控制作用 [25] ,
对系统(1)的混沌动力学行为起着控制作用 [25] ,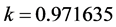 被称为类似黄金分割数0.6183比例的系统(1)混沌状态临界点,此时的KAM (Kolmogorov-Arnold-Mosser)曲线被称不变黄金曲线,其相位空间图如图1(b)所示,这个图展示了由光滑函数产生各种保面积不变的经典相位空间结构,即某些稳定的‘岛礁’嵌入到一片混沌海域里面,而且在相同的结构在越来越小的量级上出现,呈现分形现象,在黄金分割数不变曲线的附近相位图上出现‘黄金尾巴’,这时的相位空间对所有光滑函数是普遍的,当参数
被称为类似黄金分割数0.6183比例的系统(1)混沌状态临界点,此时的KAM (Kolmogorov-Arnold-Mosser)曲线被称不变黄金曲线,其相位空间图如图1(b)所示,这个图展示了由光滑函数产生各种保面积不变的经典相位空间结构,即某些稳定的‘岛礁’嵌入到一片混沌海域里面,而且在相同的结构在越来越小的量级上出现,呈现分形现象,在黄金分割数不变曲线的附近相位图上出现‘黄金尾巴’,这时的相位空间对所有光滑函数是普遍的,当参数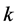 小于黄金分割数时,KAM不变曲线是有界的,当系统控制参数
小于黄金分割数时,KAM不变曲线是有界的,当系统控制参数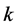 大于黄金分割数时,KAM不变曲线就变成无界的,即出现混沌状态,并且以某种扩散速度不断地扩散到整个区域。图1(a),图1(c)和图1(d)分别是当参数
大于黄金分割数时,KAM不变曲线就变成无界的,即出现混沌状态,并且以某种扩散速度不断地扩散到整个区域。图1(a),图1(c)和图1(d)分别是当参数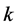 取为0.6, 1, 5对应的相位空间图,从图中可以看到,对于不动点和周期点的附近时稳定外,其他点在区域上表现为伪随机状态,而且,随着参数
取为0.6, 1, 5对应的相位空间图,从图中可以看到,对于不动点和周期点的附近时稳定外,其他点在区域上表现为伪随机状态,而且,随着参数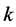 的不断增大,系统的混沌状态越明显。标准映射的Kolmogorov-Sinai熵为
的不断增大,系统的混沌状态越明显。标准映射的Kolmogorov-Sinai熵为 [26] 。
[26] 。
为了使用标准映射对图像进行置乱加密,文献 [9] 对系统(1)进行从边长为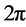 的方形区域离散化到以正整数
的方形区域离散化到以正整数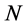 为边长的方形格子,即:令
为边长的方形格子,即:令 ,
,  ,
,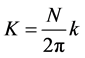 则系统(1)可变为
则系统(1)可变为
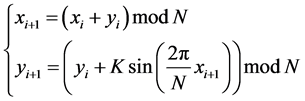 (2)
(2)
这里 是方形图像的边长,
是方形图像的边长,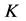 为系统参数。
为系统参数。
2.2. 标准映射的改进及其特性分析
由式子(2)易知,若我们把离散化的标准映射(2)应用到明文图像像素的位置置乱,依据混沌加密的特点,通常我们把初值和参数设为加密系统的密钥,但在这里只有一个参数 ,而且计算过程简单,这个就可能会导致加密系统的密钥空间小和随机序列容易被预测等的问题,有一定的局限性,为了有效的改变这一情况,受文献 [19] 的启发,我们在原来标准映射的基础上对系统(1)进行改进,即增加含参数的线性组合和变量的非线性项,这样就可以扩大加密系统的密钥空间和加快相邻像素相关性减弱的速度。对系统(1)改进的标准映射数学公式表示如下:
,而且计算过程简单,这个就可能会导致加密系统的密钥空间小和随机序列容易被预测等的问题,有一定的局限性,为了有效的改变这一情况,受文献 [19] 的启发,我们在原来标准映射的基础上对系统(1)进行改进,即增加含参数的线性组合和变量的非线性项,这样就可以扩大加密系统的密钥空间和加快相邻像素相关性减弱的速度。对系统(1)改进的标准映射数学公式表示如下:
 (3)
(3)
这里 ,
,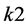 是大于0的系统控制参数,
是大于0的系统控制参数, ,
, 为非线性项的指数。
为非线性项的指数。

 (a) (b)
(a) (b)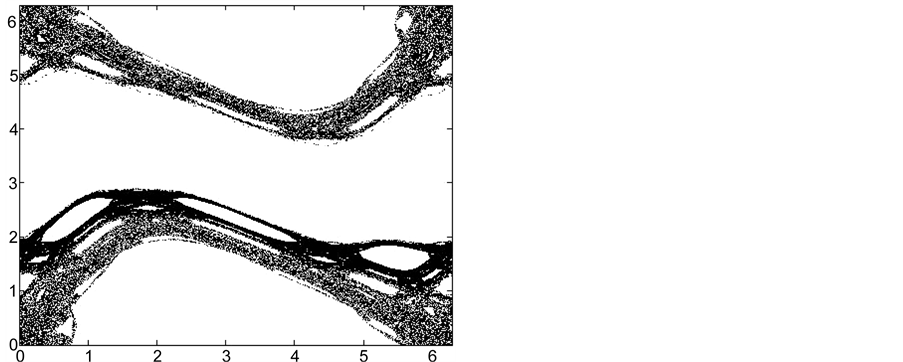
 (c) (d)
(c) (d)
Figure 1. (a)-(d) are the phase maps of the standard mapping parameters k = 0.6, 0.971635, 1, 5, respectively
图1. (a)~(d)分别为标准映射取参数k = 0.6, 0.971635, 1, 5的相位空间图
下面就改进标准映射(3)的相位空间图、Lyapunov指数谱曲线、时间序列测试和图像置乱效果来说明本文提出改进方法的有效性。
一个系统的空间相位图直观地显示了其动力学行为演化的过程,在图2,我们比较了标准映射和改进标准映射的相图,图2(a)是标准映射参数取 时的相位空间图,图2(b)则为改进标准映射参数分别取
时的相位空间图,图2(b)则为改进标准映射参数分别取 ,
, 对应的空间相位图。从图中我们发现,当我们取相同初值时,改进标准映射比标准映射更快的达到“遍历”状态,而标准映射则出现了一些稳定的区域,这说明改进标准映射比标准映射有更好的混沌特性,对设计图像加密算法来说是更有利的。
对应的空间相位图。从图中我们发现,当我们取相同初值时,改进标准映射比标准映射更快的达到“遍历”状态,而标准映射则出现了一些稳定的区域,这说明改进标准映射比标准映射有更好的混沌特性,对设计图像加密算法来说是更有利的。
指数是指在相位空间中相互靠近的两条轨道随着时间的推移,轨道之间按指数分离或聚合的平均变化率。在实际应用中,混沌系统的最大Lyapunov指数具有重要的意义,而且其计算容易在计算机上实现。在图3我们分别画出了标准映射(0Std, Original Standard Mapping)和改进标准映射(IStd, Improved Standard Mapping)的Lyapunov指数谱曲线图,即取定初值和其中一个参数,控制另外一个参数变化得到相应的Lyapunov指数。从曲线图我们看到,标准映射和改进标准映射的Lyapunov指数均有一个大于0,另一个小于0,并且随着参数的不断增大,两者Lyapunov指数的绝对值也越来越大。我们选取

 (a) (b)
(a) (b)
Figure 2. (a) and (b) are the phase maps of the standard mapping and the improved standard mapping under the same initial conditions
图2. (a), (b)分别为标准映射和改进标准映射在相同初值条件下的相位空间图

 (a) (b)
(a) (b) (c)
(c)
Figure 3. (a)-(c) are the Lyapunov exponent curves of standard mapping and improved standard mapping, respectively
图3. (a)~(c)分别为标准映射和改进标准映射不同参数的Lyapunov指数曲线图
相同的初值,不同的1000个参数值对应有1000个不同的Lyapunov指数值,求得标准映射和改进标准映射的最大Lyapunov指数平均值分别为: ,
,  ,
, 。从以上的分析表明我们改进的标准映射的混沌特性要比标准映射要更优。因此利用改进标准映射来设计加密系统是较标准映射更适合的。
。从以上的分析表明我们改进的标准映射的混沌特性要比标准映射要更优。因此利用改进标准映射来设计加密系统是较标准映射更适合的。
时间序列分析是对时间序列进行统计分析,即对某件事件大量的已有的时间序列数据,用数学的方法进行研究分析,寻找其变化规律,从而可以对未来的情况进行预测、决策和控制。在本论文中,为了更进一步说明改进的标准映射具有较好的随机性质,我们测试了改进标准映射产生时间序列的相关性,其中自相关性系数和互相关系数是两个主要的度量指标。对于两个随机时间序列 ,
, ,延迟
,延迟 阶的互相关性系数(crosscorr)和延迟
阶的互相关性系数(crosscorr)和延迟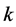 阶的自相关系数(autocorr)的数学公式定义分别如下:
阶的自相关系数(autocorr)的数学公式定义分别如下:
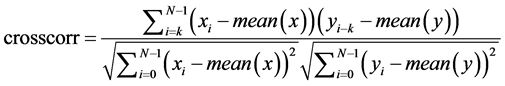 (4)
(4)
 (5)
(5)
这里 指的是序列
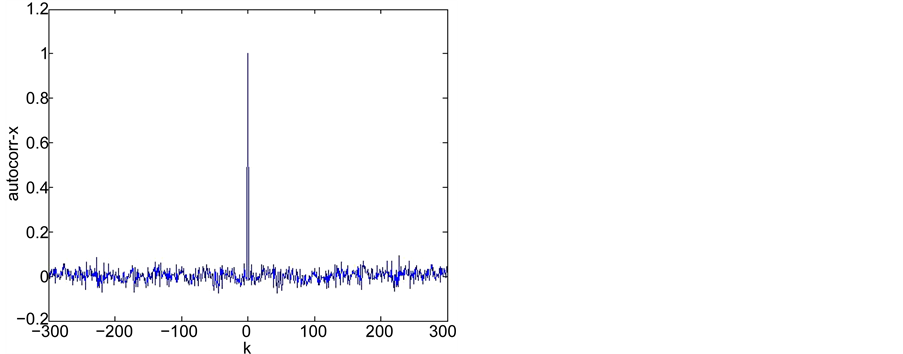
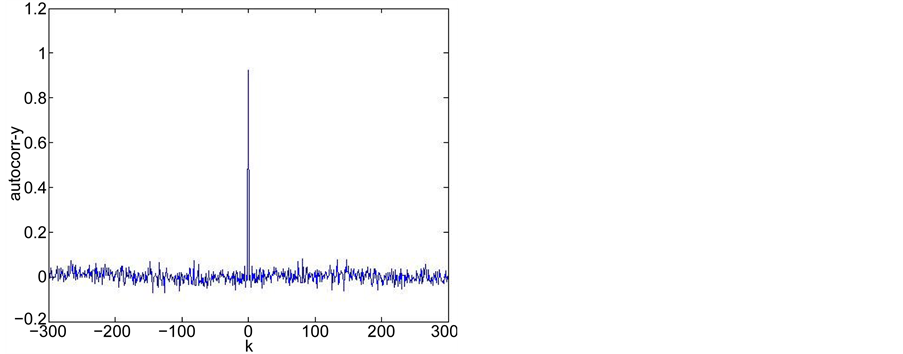
指的是序列 的算术平均值。图4是改进标准映射两个变量的时间序列图,图5分别对应变量
的算术平均值。图4是改进标准映射两个变量的时间序列图,图5分别对应变量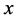 的自相关性测试、变量
的自相关性测试、变量 的自相关测试、
的自相关测试、 与
与 的互相关测试。从测试结果可以看到,改进标准映射产生的序列具有很强的随机性,因而具有不可预测性等好的密码特性,特别适合用于设计加密算法。
的互相关测试。从测试结果可以看到,改进标准映射产生的序列具有很强的随机性,因而具有不可预测性等好的密码特性,特别适合用于设计加密算法。
类似于标准映射(1)的离散方式,我们可以对改进标准映射(3)进行离散化,其离散化的数学公式表达式如下:
 (6)
(6)

 (a) (b)
(a) (b)
Figure 4. (a), (b) are the x, y time series of the improved standard mapping, respectively
图4. (a), (b)分别是改进标准映射的x, y时间序列
 (a) (b)
(a) (b) (c)
(c)
Figure 5. (a)-(c) are the auto-correlation and cross-correlation test results of the time series generated by the improved standard mapping, respectively
图5. (a)~(c)分别为改进标准映射产生时间序列的自相关性和互相关性测试结果
这里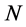 为方形图像行或列的像素个数。
为方形图像行或列的像素个数。 ,
,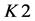 为大于1的正整数,
为大于1的正整数, ,
,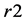 为正整数。为了兼顾计算机运行速度和计算复杂性,
为正整数。为了兼顾计算机运行速度和计算复杂性,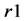 ,
, 的值不应取得太大。在应用离散改进标准映射对图像进行置乱时,为了避免出现
的值不应取得太大。在应用离散改进标准映射对图像进行置乱时,为了避免出现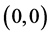 点不改变位置的特殊情况,类似于文献 [18] ,我们引入数对
点不改变位置的特殊情况,类似于文献 [18] ,我们引入数对 ,其中
,其中 ,
, 为正整数,即对(6)式做如下变形:
为正整数,即对(6)式做如下变形:
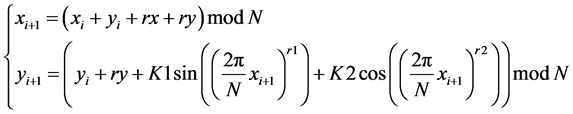 (7)
(7)
图6,图7分别显示了离散化的标准映射(2)与离散化的改进标准映射(7)对大小为 的灰度图像Lena的置乱效果。这里
的灰度图像Lena的置乱效果。这里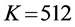 ,
, ,
, ,
, ,
, ,
, 。从图中我们可以比较发现,离散化的改进标准映射(7)的第2轮置乱就出现了不可识别的雪花图,但标准映射置乱2次后仍然出现了纹理状的置乱图,这就说明了改进标准映射的置乱效果比标准映射要好很多。我们第2节将利用离散化的改进标准映射(7)来设计对灰度图像的加密算法。
。从图中我们可以比较发现,离散化的改进标准映射(7)的第2轮置乱就出现了不可识别的雪花图,但标准映射置乱2次后仍然出现了纹理状的置乱图,这就说明了改进标准映射的置乱效果比标准映射要好很多。我们第2节将利用离散化的改进标准映射(7)来设计对灰度图像的加密算法。



 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 6. (a)-(d) correspond to the plaintext and the scrambled image after the standard mapping scrambling 1, 2, 3 times
图6. (a)~(d)分别对应明文和用标准映射置乱1, 2, 3轮的置乱图像



 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 7. (a)-(d) correspond to the plaintext and the scrambled image after the improved standard mapping scrambling 1, 2, 3 times
图7. (a)~(d)分别对应明文和用改进标准映射置乱1, 2, 3轮的置乱图像
3. 基于改进标准映射的图像加密算法
基于以上的结果和分析,我们在这一节设计一种基于改进标准映射的灰度图像加密算法。这个算法采用传统的置乱–扩散结构。在置乱阶段,利用离散化的改进标准映射(7)对明文图像进行像素位置的置乱,我们提出的算法只需置乱3次就可达到杂乱无章且没有纹理的置乱图;在像素扩散阶段,采用动态反馈的扩散方式,利用已经加密的密文和由改进标准映射产生密钥去加密置乱后的图像像素灰度值,进而使加密效果更优。在这个算法中,我们选取明文图像像素的SHA256哈希函数值作为加密系统密钥的一部分,如果明文的像素改变很微小甚至1比特值,均会引起完全不同的明文SHA256哈希值,这也就说明了我们的密钥对明文是极端敏感的,同时也使得我们的加密算法能够很好的抵御明文攻击和差分攻击。不失一般性,我们不妨记明文图像为I,且其大小为 ,
, ,
,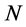 分别为像素矩阵的行数和列数。明文图像像素的SHA256哈希函数值记为
分别为像素矩阵的行数和列数。明文图像像素的SHA256哈希函数值记为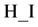 ,算法的具体步骤如下所阐述:
,算法的具体步骤如下所阐述:
Step 1. 读入明文,输入密钥。读入明文图像I,并记 ,计算明文图像的SHA256哈希函数值
,计算明文图像的SHA256哈希函数值 ,并将其转化为一个大小为
,并将其转化为一个大小为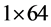 的向量
的向量 ,设置要执行图像置乱的次数iter,输入改进标准映射的参数
,设置要执行图像置乱的次数iter,输入改进标准映射的参数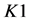 ,
,  ,
, 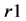 ,
, 。
。
Step 2. 计算防止出现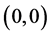 置乱无效的整数对
置乱无效的整数对 。首先计算向量
。首先计算向量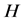 的大小和所有元素的和,分别记为
的大小和所有元素的和,分别记为 ,
,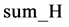 ,然后选取向量
,然后选取向量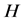 的奇数项和偶数项的元素并分别求和,分别记为
的奇数项和偶数项的元素并分别求和,分别记为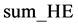 ,
, ,最后分别利用(8), (9)式计算
,最后分别利用(8), (9)式计算 ,
, 。
。
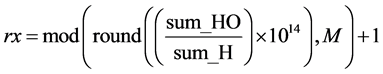 (8)
(8)
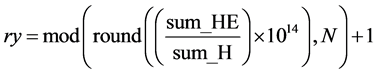 (9)
(9)
Step 3. 利用离散化改进标准映射(7)对明文灰度图像像素的位置进行置乱iter次,置乱后的图像矩阵记为I1。
Step 4. 利用公式(10), (11)计算改进标准映射(3)式的初值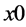 ,
, 。
。
 (10)
(10)
 (11)
(11)
Step 5. 计算改进标准映射的两个新参数 ,
, ,和为了避免产生过渡效应的迭代步数
,和为了避免产生过渡效应的迭代步数 。具体计算过程通过以下(12), (13), (14)式得到:
。具体计算过程通过以下(12), (13), (14)式得到:
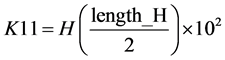 (12)
(12)
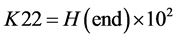 (13)
(13)
 (14)
(14)
Step 6. 以 ,
, 为初值,
为初值,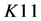 ,
,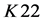 为参数,迭代改进标准映射(3)式
为参数,迭代改进标准映射(3)式 次,产生两个序列
次,产生两个序列 ,
,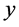 ,为了避免量化过程出现的过渡效应发生的情况,我们把
,为了避免量化过程出现的过渡效应发生的情况,我们把 ,
,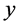 的前
的前 项丢弃。这样我们就得到两个大小均为
项丢弃。这样我们就得到两个大小均为 的向量
的向量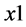 ,
, 。
。
Step 7. 利用Step 6生成的两个随机序列产生3个密钥流,记为key 1, key 2, key 3。其计算公式如下(15), (16), (17)式:
 (15)
(15)
 (16)
(16)
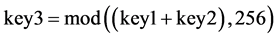 (17)
(17)
Step 8. 将置乱后的图像矩阵I1重新排成一个一维向量I2。依据以下(18)式从上到下,从左到右的顺序排成一行,同时利用(19)式计算除了I2第一项以外的所有元素的和,记为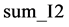 ,最后根据(20)式产生一个种子值seed。
,最后根据(20)式产生一个种子值seed。
 (18)
(18)
 (19)
(19)
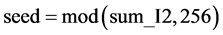 (20)
(20)
Step 9. 计算用来加密置乱后I2的第1个元素的密钥 。这里根据(21)式来计算,该值与key 1和key 2有关。
。这里根据(21)式来计算,该值与key 1和key 2有关。
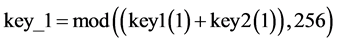 (21)
(21)
Step 10. 加密置乱后图像I2的第1个元素。即是对向量I2的第1个元素进行扩散产生最后的密文I3的第1项。扩散公式(22)如下:
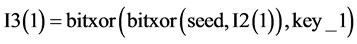 (22)
(22)
Step 11. 设置 ,计算用来加密置乱后元素的动态指数
,计算用来加密置乱后元素的动态指数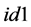 ,
, 。这2个动态指数与已经加密过后的元素和由(15), (16)产生的密钥有关,数学计算公式如下(23), (24)所示:
。这2个动态指数与已经加密过后的元素和由(15), (16)产生的密钥有关,数学计算公式如下(23), (24)所示:
 (23)
(23)
 (24)
(24)
Step 12. 采用Step 11产生的 ,
, 根据如下式(25)对置乱后的图像I2的第
根据如下式(25)对置乱后的图像I2的第 项进行加密,直到
项进行加密,直到 。
。
 (25)
(25)
Step 13. 对置乱后图像I2的最后一个像素加密。首先利用式(26)计算类似Step 12的指数,然后用式(27)对I2的最后一个像素进行加密。然后把I3拉成一个新的2维矩阵I4,即为我们的最终加密密文。
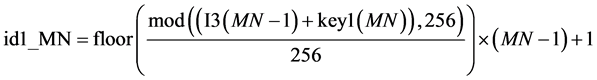 (26)
(26)
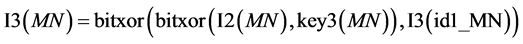 (27)
(27)
以上加密过程中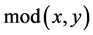 是指实数
是指实数 除以实数
除以实数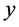 得到的余数,
得到的余数, 是指对实数
是指对实数 的四舍五入取整函数,
的四舍五入取整函数, 返回不超过实数
返回不超过实数 的最大的整数,
的最大的整数,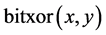 返回的是实数
返回的是实数 与实数
与实数 的按位异或运算结果,
的按位异或运算结果,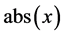 是指对实数
是指对实数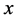 的取绝对值运算。本文提出加密算法的流程图见图8,解密过程是加密过程的逆过程,其大致流程图如图9,这里值得注意的是,在逆扩散阶段要从逆序开始解密,即采用相同密钥做逆运算。详细步骤这里不再赘述。
的取绝对值运算。本文提出加密算法的流程图见图8,解密过程是加密过程的逆过程,其大致流程图如图9,这里值得注意的是,在逆扩散阶段要从逆序开始解密,即采用相同密钥做逆运算。详细步骤这里不再赘述。
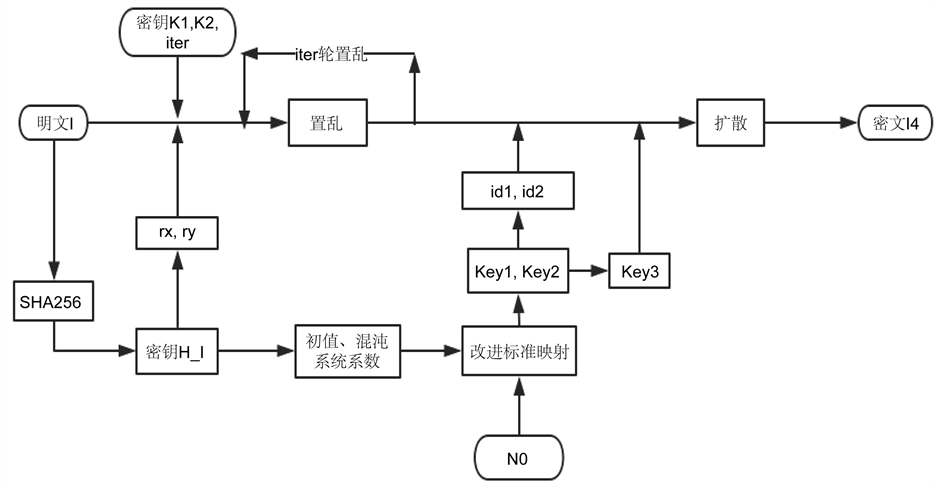
Figure 8. The flow chart of encryption algorithm based on improved standard mapping
图8. 基于改进标准映射的加密算法流程图

Figure 9. The flow chart of decryption algorithm based on improved standard mapping
图9. 基于改进标准映射的解密算法流程图
4. 仿真实验和加密性能分析
4.1. 仿真实验
在这一部分,我们采用MATLABR2014a软件对本文提出的基于改进标准映射的灰度图像加密算法进行仿真实验。所有的实验均在同一台个人电脑上实现与执行,电脑的主要硬件环境如下:处理器:Intel(R)Core(TM) i7-5500CPU@2.40 GHz 2.39 GHz,安装内存:4.00 GB;运行系统:Windows 8.1中文版。另外,本文所有的实验图像均来自文献 [27] 的图像数据库。在仿真实验过程中我们采用的密钥空间由以下部分组成: ,我们分别对三幅灰度图像即Lena, Elaine, Man用本文提出的加密算法进行加密,它们的图像尺寸分别为
,我们分别对三幅灰度图像即Lena, Elaine, Man用本文提出的加密算法进行加密,它们的图像尺寸分别为 ,
, 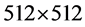 ,
,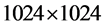 ,用密钥
,用密钥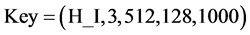 进行仿真实验,其结果如图10所示,从这些明文、密文和解密文图中我们可以看到,所有的密文都呈现杂乱无章且无明显纹理出现,攻击者不能从其中获取任何有关明文图像的信息,因而对明文图像起到了很好的保护作用,这说明了我们的算法有一个好的加密效果,而且所有的密文都可以通过正确的加密密钥来获得与明文完全一样的图像,这也表明本文提出算法是一种无损的图像加密算法。
进行仿真实验,其结果如图10所示,从这些明文、密文和解密文图中我们可以看到,所有的密文都呈现杂乱无章且无明显纹理出现,攻击者不能从其中获取任何有关明文图像的信息,因而对明文图像起到了很好的保护作用,这说明了我们的算法有一个好的加密效果,而且所有的密文都可以通过正确的加密密钥来获得与明文完全一样的图像,这也表明本文提出算法是一种无损的图像加密算法。
4.2. 加密性能分析
一个加密算法鲁棒性强弱的一个重要度量是加密系统抵抗攻击者从密文图像中获取任何有关于明文图像信息的能力大小。一个鲁棒性强的算法还应该能够抵抗绝大多数的已知攻击,比如已知明文或选择明文攻击、选择密文攻击和各种蛮力攻击等。为了检验本文提出算法的鲁棒性强弱,对于图像加密算法的重要安全分析如密钥空间分析、统计分析和密钥敏感性分析等,均在这一小节讨论。
一个图像加解密算法的密钥空间是指能够用在加解密算法过程中密钥的所有可能取值的总和。如果一个算法的密钥空间足够大,很多非法攻击如暴力攻击等将会变得不可实现,从今天的计算机的计算精度来看,对于普通加密的实际应用中,大于128 bit的密钥空间一般被认为是安全的 [17] 。在本文提出的灰度图像加密算法中,如果我们把密钥空间取为由 所组成的空间大小,其中,
所组成的空间大小,其中, 是明文的SHA256哈希值,其可能取值为2128 [16] 。而
是明文的SHA256哈希值,其可能取值为2128 [16] 。而 是图像加密算法过程中置乱的轮数,我们不妨取其数量级为103,太大可能会出现周期的现象。对于
是图像加密算法过程中置乱的轮数,我们不妨取其数量级为103,太大可能会出现周期的现象。对于 ,
, ,如果我们取双精度数据的精度作为计算
,如果我们取双精度数据的精度作为计算
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
 (e)
(e)
 (f)
(f)
 (g)
(g)
 (h)
(h)
 (i)
(i)
Figure 10. (a)-(i) correspond to the plain-text, cipher-text, and decrypted images of images Lena (a), Elaine (d), Man (g)
图10. (a)~(i)分别对应图像Lena (a), Elaine (d), Man (g)的明文、密文和解密图像
时,那么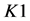 ,
, 的可能取值的量级均为
的可能取值的量级均为 。
。 是为了避免产生过渡效应的改进标准映射预先迭代次数,为了不增加整个加密的运算时间,我们取
是为了避免产生过渡效应的改进标准映射预先迭代次数,为了不增加整个加密的运算时间,我们取 的量级为104。这样我们就可以得到提出的基于改进标准映射的图像加密算法的密钥空间大小,即
的量级为104。这样我们就可以得到提出的基于改进标准映射的图像加密算法的密钥空间大小,即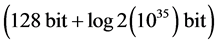 ,这个值远远大于理想值128 bit。而且,如果我们考虑把非线性项的指数
,这个值远远大于理想值128 bit。而且,如果我们考虑把非线性项的指数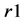 ,
,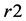 作为密钥的一部分,那么我们的加密系统的密钥空间将更大。这就说明了我们提出的图像加密算法具有非常大的密钥空间,它足以抵抗各种蛮力攻击。
作为密钥的一部分,那么我们的加密系统的密钥空间将更大。这就说明了我们提出的图像加密算法具有非常大的密钥空间,它足以抵抗各种蛮力攻击。
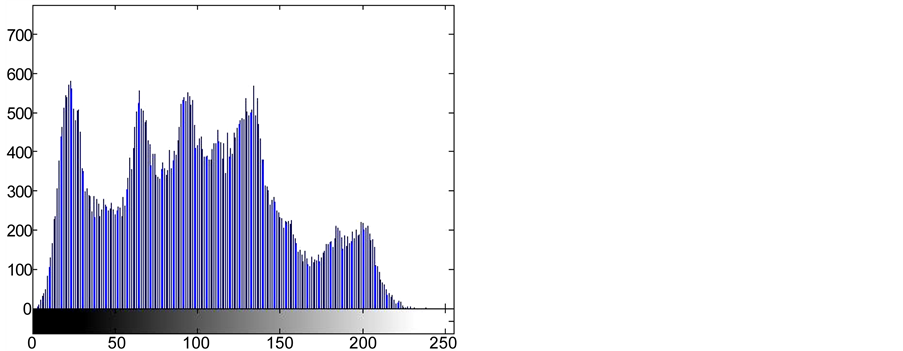
一幅图像的灰度直方图是表示一幅图像灰度分布的统计图表 [28] 。直方图的横坐标是灰度级,纵坐标是具有给灰度级的像素个数或者出现这个灰度级的概率或频率。由于每个灰度级对应的概率或频率给出了对该灰度级出现的概率估计,所以直方图提供了图像的灰度值分布情况,即给出了一幅图像所有灰度值的整体描述。对于一幅8比特的灰度图像,其灰度值可能有28种不同的取值,因此,灰度图像的直方图显示了256种不同灰度值的分布情况。对于一个鲁棒性强的灰度图像加密算法,应用该算法加密得到的密文图像的像素灰度值应该有一致分布的趋势。在本文提出的算法中,采用大小为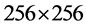 的灰度图像Lena为测试图像,Key为密钥空间,利用本文提出算法加密测试图像并分别画出明文和密文的灰度直方图,如图11所示,从图中我们可以看到,密文的直方图分布明显的比明文的直方图不同,密文直方图呈现分布基本一致的趋势,但明文图像的直方图分布波动情况较密文图像的直方图大,这也就说明我们提出的图像加密算法不能给攻击者提供任何有关明文图像的统计信息,即我们提出的加密算法是具有强鲁棒性的。
的灰度图像Lena为测试图像,Key为密钥空间,利用本文提出算法加密测试图像并分别画出明文和密文的灰度直方图,如图11所示,从图中我们可以看到,密文的直方图分布明显的比明文的直方图不同,密文直方图呈现分布基本一致的趋势,但明文图像的直方图分布波动情况较密文图像的直方图大,这也就说明我们提出的图像加密算法不能给攻击者提供任何有关明文图像的统计信息,即我们提出的加密算法是具有强鲁棒性的。
一维灰度直方图采用灰度级出现次数统计的均匀性来评价图像加密的效果,有时会难以看清具体的像素分布,因为在一维直方图中,失去了图像本身具有像素空间位置信息,即二维特征,一幅图像对应一个直方图,但一个直方图并不一定只对应一幅图像。所以,引入像素与其相邻像素所对联合空间统计量,即共生直方图,来更好的对图像加密算法的分析,在图12分别画出了明文图像Lena与其对应本文
 (a) (b)
(a) (b)
Figure 11. (a)-(b) correspond to the Lena image and cipher-text histogram
图11. (a)~(b)分别对应Lena图像和密文的直方图
 (a) (b)
(a) (b)
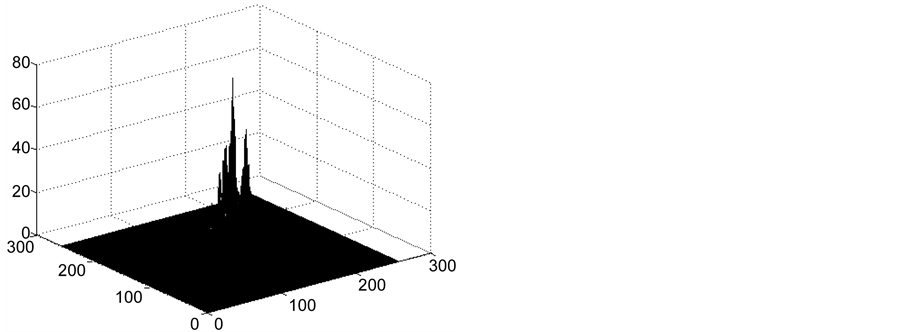
Figure 12. (a)-(b) correspond to the symbiotic histogram of Lena image and cipher-text respectively
图12. (a)~(b)分别对应 图像和密文的共生直方图
算法得到的密文图像的共生直方图。从图中我们可以观察到,密文图像的共生直方图分布显得更均匀,攻击者不能够从密文的共生直方图得到任何有关明文图像的信息,而明文图像则明显波动起伏大,这更说明了本文提出算法有非常好的的鲁棒性。
在1949年,Shannon [17] 提出了一个反映一个信息源的随机性和不可预测性的数学概念,即信息熵。它以bits或字符号量化包含在随机数据里面的信息,信息熵也是信息作为载体能进行通信的最小长度,换句话说,信息熵是测量信息无序状态的度量,如一个重复字符的长序列,由于其每一个字符是可预测的,即其每一个字符出现概率是1,我们可以由信息熵的定义式(28)知道在这个序列的信息熵为0,而对于一个完全随机的序列,因为没有办法预测序列下一个字符,所以该序列有一个最大的信息熵。一个信息源m的信息熵 的数学计算公式如下(28)式:
的数学计算公式如下(28)式:
 (28)
(28)
这里 是在信息m中
是在信息m中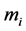 发生的概率,
发生的概率,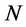 是指在信息源m中表达一个字符所需要的bit位个数。对于灰度图像,
是指在信息源m中表达一个字符所需要的bit位个数。对于灰度图像, 。一个在0到255范围内一致分布的随机图像,就是说,每个灰度值出现的概率相同,那么由(28)式,我们容易计算其信息熵的理想值为8。所以,对于图像加密来说,加密图像的信息熵值越接近于8,则图像加密系统泄漏有关明文信息的可能性就越小。为了说明本文提出算法对于信息熵攻击是鲁棒性的,我们分别计算了不同大小的明文(Lena, Elaine, Man)的信息熵和它们对应密文图像的信息熵,结果如表1所示,从表1我们可以看到,明文图像的信息熵明显小于密文的值,而密文的信息熵都接近理想值8,特别是当图像的大小为
。一个在0到255范围内一致分布的随机图像,就是说,每个灰度值出现的概率相同,那么由(28)式,我们容易计算其信息熵的理想值为8。所以,对于图像加密来说,加密图像的信息熵值越接近于8,则图像加密系统泄漏有关明文信息的可能性就越小。为了说明本文提出算法对于信息熵攻击是鲁棒性的,我们分别计算了不同大小的明文(Lena, Elaine, Man)的信息熵和它们对应密文图像的信息熵,结果如表1所示,从表1我们可以看到,明文图像的信息熵明显小于密文的值,而密文的信息熵都接近理想值8,特别是当图像的大小为 时,其信息熵的值可以达到7.9998,这说明本文提出图像加密算法对于信息熵攻击是强鲁棒性的。为了进一步说明本文算法的强鲁棒性,我们用文献 [15] 的加密算法去加密相同的明文,并计算其信息熵如表1最后一行所示,比较易知,我们提出的算法加密效果是优于文献 [15] 的。
时,其信息熵的值可以达到7.9998,这说明本文提出图像加密算法对于信息熵攻击是强鲁棒性的。为了进一步说明本文算法的强鲁棒性,我们用文献 [15] 的加密算法去加密相同的明文,并计算其信息熵如表1最后一行所示,比较易知,我们提出的算法加密效果是优于文献 [15] 的。
对于一幅有有限视觉内容的自然图像,每个像素无论是在水平方向、垂直方向还是在对角方向都与其相邻的像素高度相关。一个理想的图像加密算法应该产生在各个方向上的相邻像素相关性都很弱的密文图像。为了量化和比较在明文和密文像素在水平、垂直与对角方向的相关性,我们从明文Lena和其对应应用本文提出算法加密的密文中随机地分别选取三个不同方向5000对像素,我们通过式(29)来计算随机选取的两个像素序列的相关性,表2列举出了不同方向像素相关系数的计算结果,在图13画出了从明文和密文选取的像素点分布。我们从表2可以看到,明文图像无论在水平方向、垂直方向还是在对角方向明文图像的相关系数都接近于理想值1,而经过本文提出算法加密后的密文则显得其相关性系数很小,几乎为0。另一方面,我们观察图13易知,明文的像素点呈现线性分布,而明文图像像素点则显得杂乱
Table 1. Information entropy of different plain-text and cipher-text corresponding to different encryption algorithms
表1. 不同明文图像和对应不同加密算法密文图像的信息熵
Table 2. The correlation coefficient between Lena and its cipher-text in horizontal, vertical and diagonal directions, respectively
表2. Lena与其密文分别在水平、垂直和对角方向上的相关系数


 (a) (b) (c)
(a) (b) (c)

 (d) (e) (f)
(d) (e) (f)
Figure 13. (a)-(c), (d)-(f) are the distributions of Lena and cipher-text pixels in horizontal, vertical and diagonal directions, respectively
图13. (a)~(c), (d)~(f)分别为Lena和密文在水平、垂直和对角方向像素的分布
无章的无序状态,所以本文提出的算法成功地消除了明文相邻像素相关性,从而本文算法对于统计分析是强鲁棒的。
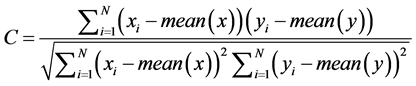 (29)
(29)
这里 是指序列
是指序列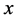 的均值。
的均值。
对于一个有效的图像加密算法,密文图像与明文图像应该有很大的不同,而且密文应该是对明文图像的较低矫正,在这里,我们通过计算二维相关系数来分析明文A和密文B的之间的关系,二维相关系数的数学计算公式如(30)示,我们计算了不同大小的明文(Lena, Elaine, Man)和它们对应的用本文提出算法加密密文的二维相关系数,结果如表3所示,从表3易知,不同明文图像与对应密文图像的相关性很小,几乎等于0,这就说明的密文是与明文彼此的相关性非常的弱,存在很大的差别,呈现随机性分布,从而反映本文提出加密算法的有效性。
Table 3. The correlation coefficient between plain-text and cipher-text
表3. 明文与密文的相关性系数
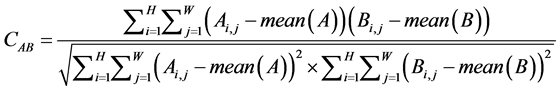 (30)
(30)
在这里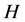 ,
, 分别表示图像矩阵的大小,
分别表示图像矩阵的大小, 表示序列
表示序列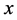 的均值。
的均值。
在某种程度上使一个加密算法抵抗蛮力攻击的一个重要保证是加密系统对密钥极端敏感。一个加密系统的密钥敏感性一般通过两方面来考察,一方面,由提出加密算法加密的密文图像应该极端敏感于密钥,就是说,如果我们用两个差别很微小的密钥加密同一明文,那么相应密钥产生的密文应该完全不依赖于明文或者是他们之间的相关性可以忽略,即他们之间的差别应该非常大。另一方面,尽管在加密和解密过程的密钥相差非常的微小,但不能够用解密算法来解得加密明文。在我们提出的算法中,密钥组成为 ,首先,我们采用密钥
,首先,我们采用密钥 对Lena进行加密得到其加密图像。然后分别采用五个不同的密钥Key 1 ~ Key 5对同一幅明文Lena进行加密并分别与用Key产生的密文作比较产生差别图diff,其中H_I1是明文图像随机改变1 bit值后的SHA256哈希函数值,比较结果如图14所示,从图中可以明显观察到,采用不同密钥对同一明文进行加密时,所产生的密文图像跟用Key加密产生的密文相差非常大的,甚至是完全不一样的,另外我们计算出Key产生的密文与其他五个密钥产生的结果之间的二维相关系数,其计算公式如式子(30)所示,计算结果如表4所示,从表中我们可以看到,不同密钥甚至差别仅仅1 bit所产生的密文之间的相关性非常的弱,其相关系数几乎为0。由以上所述,我们从密钥敏感性的第一方面说明了我们提出算法是对密钥敏感的。同样的,我们可以验证密钥敏感性的另一方面,我们用与加密过程相同的密钥Key对应用它本身加密得到的密文进行解密,然后分别用改变了的5个不同的密钥对应用用密钥Key产生的密文进行解密,得到的结果如表5和图15所示,从表5我们很明显的可以看到,用改变仅微小变化的错误密钥和正确密钥得到的明文之间的相关性非常的弱,它们对应的相关系数几乎为零,另外,从图15中可以看出加密系统是对密钥空间敏感的,因而我们提出的加密系统是具有强鲁棒性的。5个仅改变微小变化的密钥分别表示为如下式子:
对Lena进行加密得到其加密图像。然后分别采用五个不同的密钥Key 1 ~ Key 5对同一幅明文Lena进行加密并分别与用Key产生的密文作比较产生差别图diff,其中H_I1是明文图像随机改变1 bit值后的SHA256哈希函数值,比较结果如图14所示,从图中可以明显观察到,采用不同密钥对同一明文进行加密时,所产生的密文图像跟用Key加密产生的密文相差非常大的,甚至是完全不一样的,另外我们计算出Key产生的密文与其他五个密钥产生的结果之间的二维相关系数,其计算公式如式子(30)所示,计算结果如表4所示,从表中我们可以看到,不同密钥甚至差别仅仅1 bit所产生的密文之间的相关性非常的弱,其相关系数几乎为0。由以上所述,我们从密钥敏感性的第一方面说明了我们提出算法是对密钥敏感的。同样的,我们可以验证密钥敏感性的另一方面,我们用与加密过程相同的密钥Key对应用它本身加密得到的密文进行解密,然后分别用改变了的5个不同的密钥对应用用密钥Key产生的密文进行解密,得到的结果如表5和图15所示,从表5我们很明显的可以看到,用改变仅微小变化的错误密钥和正确密钥得到的明文之间的相关性非常的弱,它们对应的相关系数几乎为零,另外,从图15中可以看出加密系统是对密钥空间敏感的,因而我们提出的加密系统是具有强鲁棒性的。5个仅改变微小变化的密钥分别表示为如下式子:
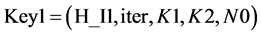 ,
,  ,
,
 ,
, 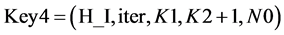 ,
,
 .
.
4.2.7. 差分分析
图像加密算法的差分加密分析是研究在相同加密密钥的条件下明文图像的改变会在多大程度上能够影响密文图像,攻击者通常通过选择明文分析或选择密文分析来实现。对于一个图像加密系统来说,实现差分分析的一般做法是仅改变明文图像像素的微小变化(通常是1 bit或1个单位像素值),然后比较在同一密钥条件下分别对明文图像和改变的明文图像进行加密得到两个密文图像,如果在明文图像和密文图像之间我们能够找到一些有利于确定加密密钥的信息,那么这样的分析就说明加密算法的鲁棒性很弱,反之,如果我们仅改变明文图像1 bit的变化,加密算法就能够产生有意义、随机且不可预测的密文
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
 (e)
(e)
 (f)
(f)
 (g)
(g)
 (h)
(h)
 (i)
(i)
 (j)
(j)
Figure 14. Encryption sensitivity test: (a), (c), (e), (g), (i) were encrypted with Key 1 - Key 5, respectively; (b), (d), (f), (h), (j) correspond to the difference between cipher-text generated by (a), (c), (e), (g), (i) and cipher-text generated by Key, respectively
图14. 加密敏感性测试: (a), (c), (e), (g), (i)分别为Key 1~Key 5应用本文提出算法加密结果; (b), (d), (f), (h), (j)分别为(a), (c), (e), (g), (i)与密钥Key产生的密文之间的差别
Table 4. The correlation coefficients between different cipher-texts generated by different keys
表4. 不同密钥产生的不同密文之间的相关性系数
注:表中Key表示用密钥Key应用本文提出算法得到的密文图像,其余类似。
Table 5. The correlation coefficients between plaintexts decrypted by different keys
表5. 不同密钥解密生成的明文之间的相关性系数
注:表中Key表示用密钥Key应用本文提出算法得到的解密图像,其余类似。



 (a) (b) (c) (d)
(a) (b) (c) (d)
 (e) (f)
(e) (f)
Figure 15. (a)-(f) are plain-texts by using Key and Key 1 - Key 5 to decrypt the cipher-text generated by Key
图15. (a)~(f)分别为用Key和Key 1~Key 5去解密Key所产生密文的明文
图像变化,这样的加密算法会使得差分分析不能够获取任何有关明文或密钥的信息,即差分分析无效。为了测试提出的图像加密算法抵抗差分分析的鲁棒性强弱,采用两个常用的度量:不同密文图像之间的像素改变率(number of piexls change rate, NPCR)和不同密文图像之间的一致改变强度(unified average changing intensity, UACI),它们的数学公式定义如下:
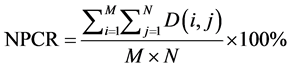 (31)
(31)
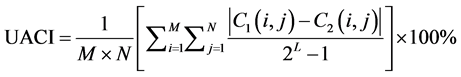 (32)
(32)
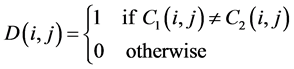 (33)
(33)
这里 ,
, 分别是矩形图像的行数和列数,
分别是矩形图像的行数和列数, 是表达一个图像像素所需要的bit位个数,对于灰度图像,它的值为
是表达一个图像像素所需要的bit位个数,对于灰度图像,它的值为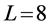 。
。 ,
, 分别是明文图像的密文和明文图像仅微小改变后的密文。对于一个理想的图像加密系统在仅改变微小变化后产生的两幅不同的随机图像来说,NPCR,UACI的值估计如下:
分别是明文图像的密文和明文图像仅微小改变后的密文。对于一个理想的图像加密系统在仅改变微小变化后产生的两幅不同的随机图像来说,NPCR,UACI的值估计如下:
 (34)
(34)
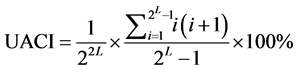 . (35)
. (35)
对于一个灰度图像来说,我们容易计算得到NPCR, UACI的理想估计值分别为99.6094%, 33.4636%。在本文提出的图像加密算法中,我们随机的选取明文图像的500个像素值,对每个灰度值仅随机改变1 bit像素值,然后我们用本文提出加密算法去加密改变前后的明文图像Lena,得到500个NPCR, UACI值,

 (a) (b)
(a) (b)
Figure 16. (a)-(b) are the NPCR and UACI graphs, respectively
图16. (a)~(b)分别为NPCR和UACI曲线图
它们的曲线变化图如图16所示,我们可以观察到NPCR, UACI值均在理想值上下波动,这500个NPCR,UACI的均值99.6195%, 33.4567%,很明显,这些值是非常接近理想估计值的,于是,我们提出的算法对差分分析是强鲁棒性的。
5. 总结
本文提出了基于改进标准映射的灰度图像加密算法。首先,对运用以往标准映射进行加密的图像加密算法比较发现,标准映射的参数空间很小和计算复杂性相对简单,于是对标准映射进行改进,增加了变量的非线性项和含参数的线性组合,以增加映射的参数空间,我们对改进标准映射进行了相位空间图、Lyapunov指数、时间序列的分析,分析结果表明,改进标准映射具有较好的混沌特性,即伪随机性、遍历性等。然后利用改进的标准映射设计了一种对灰度图像进行加密的算法,在加密的扩散阶段采用了动态反馈模式机制。最后我们对本文提出的灰度图像加密算法进行了各种各样的性能分析,包括密钥分析、密钥敏感性分析、统计分析等,所有的性能分析显示,本文提出的灰度图像加密算法具有较强的鲁棒性,非常适合实时数字图像加密。
文章引用
陈裕城,叶瑞松. 基于改进标准映射的图像加密算法
A Novel Image Encryption Algorithm Based on Improved Standard Mapping[J]. 计算机科学与应用, 2017, 07(08): 753-773. http://dx.doi.org/10.12677/CSA.2017.78087
参考文献 (References)
- 1. http://www.xinhuanet.com/world/ljm2013/index.htm
- 2. http://finance.qq.com/a/20170119/003242.htm
- 3. 张同锋. 基于一维复合混沌映射的数字图像加密算法研究[D]: [博士学位论文]. 兰州: 兰州大学, 2016.
- 4. Liu, W., Sun, K. and Zhu, C. (2016) A Fast Image Encryption Algorithm Based on Chaotic Map. Optics and Lasers in Engineering, 84, 26-36.
- 5. 张强, 田小平. 基于图像位平面分解的混沌加密方法研究[J]. 西安邮电学院学报, 2010, 15(5): 83-86.
- 6. Robinson, R.C., 韩茂安, 邢业朋, 等. 动力系统导论[M]. 北京: 机械工业出版社, 2007.
- 7. Alvarez, G. and Li, S. (2006) Some Basic Cryptographic Requirements for Chaos-Based Cryptosystems. International Journal of Bifurcation and Chaos, 16, 2129-2151. https://doi.org/10.1142/S0218127406015970
- 8. Matthews, R. (1989) On the Derivation of a “Chaotic” Encryption Algorithm. Cryptologia, 13, 29-42. https://doi.org/10.1080/0161-118991863745
- 9. Fridrich, J. (1998) Symmetric Ciphers Based on Two-Dimensional Chaotic Maps. International Journal of Bifurcation and Chaos, 8, 1259-1284. https://doi.org/10.1142/S021812749800098X
- 10. Ye, R. (2011) A Novel Chaos-Based Image Encryption Scheme with an Efficient Permutation-Diffusion Mechanism. Optics Communications, 284, 5290-5298.
- 11. Wong, K.W., Kwok, B.S.H. and Law, W.S. (2008) A Fast Image Encryption Scheme Based on Chaotic Standard Map. Physics Letters A, 372, 2645-2652.
- 12. 李昌刚, 韩正之, 张浩然. 一种基于随机密钥及“类标准映射”的图像加密算法[J]. 计算机学报, 2003, 26(4): 465- 470.
- 13. Xu, L., Gou, X., Li, Z., et al. (2017) A Novel Chaotic Image Encryption Algorithm Using Block Scrambling and Dynamic Index Based Diffusion. Optics and Lasers in Engineering, 91, 41-52.
- 14. Hamdi, M., Rhouma, R. and Belghith, S. (2017) A Selective Compression-Encryption of Images Based on SPIHT Coding and Chirikov Standard Map. Signal Processing, 131, 514-526.
- 15. Fu, C., Chen, J., Zou, H., et al. (2012) A Chaos-Based Digital Image Encryption Scheme with an Improved Diffusion Strategy. Optics Express, 20, 2363-2378. https://doi.org/10.1364/OE.20.002363
- 16. Chai, X., Chen, Y. and Broyde, L. (2017) A Novel Chaos-Based Image Encryption Algorithm Using DNA Sequence Operations. Optics and Lasers in Engineering, 88, 197-213.
- 17. Patidar, V., Pareek, N.K., Purohit, G., et al. (2011) A Robust and Secure Chaotic Standard Map Based Pseudorandom Permutation-Substitution Scheme for Image Encryption. Optics Communications, 284, 4331-4339.
- 18. Lian, S., Sun, J. and Wang, Z. (2005) A Block Cipher Based on a Suitable Use of the Chaotic Standard Map. Chaos, Solitons & Fractals, 26, 117-129.
- 19. 吴成茂. 离散Arnold变换改进及其在图像置乱加密中的应用[J]. 物理学报, 2014, 63(9): 090504.
- 20. Ye, R. (2014) A Novel Image Encryption Scheme Based on Generalized Multi-Sawtooth Maps. Fundamenta Informaticae, 133, 87-104.
- 21. Wang, Y., Wong, K.W., Liao, X., et al. (2009) A Chaos-Based Image Encryption Algorithm with Variable Control Parameters. Chaos, Solitons & Fractals, 41, 1773-1783.
- 22. Zhang, Y. and Xiao, D. (2013) Double Optical Image Encryption Using Discrete Chirikov Standard Map and Chaos-Based Fractional Random Transform. Optics and Lasers in Engineering, 51, 472-480.
- 23. Ye, R. and Huang, H. (2010) Application of the Chaotic Ergodicity of Standard Map in Image Encryption and Watermarking. International Journal of Image, Graphics and Signal Processing, 2, 19. https://doi.org/10.5815/ijigsp.2010.01.03
- 24. Zhao, J., Guo, W. and Ye, R. (2014) A Chaos-Based Image Encryption Scheme Using Permutation-Substitution Architecture. International Journal of Computer Trends and Technology, 15, 174-185. https://doi.org/10.14445/22312803/IJCTT-V15P137
- 25. Rannou, F. (1974) Numerical Study of Discrete Plane Ar-ea-Preserving Mappings. Astronomy and Astrophysics, 31, 289.
- 26. http://www.scholarpedia.org/article/Chirikov_standard_map
- 27. http://sipi.usc.edu/database/
- 28. 张弘. 数字图像处理与分析[M]. 北京: 机械工业出版社, 2013.
