Computer Science and Application
Vol.
09
No.
05
(
2019
), Article ID:
30223
,
-51
pages
10.12677/CSA.2019.95098
Application Research of MATLAB PDE Toolbox in Semiconductor Device
Ning Ma*, Zhenyu Wang, Zijun Zhu
College of Science, China University of Petroleum (Beijing), Bejing

Received: Apr. 29th, 2019; accepted: May 9th, 2019; published: May 16th, 2019

ABSTRACT
Semiconductor is a new kind of material discovered recently. Its conductivity is between conductor and insulator, and its conductivity changes with temperature. It is an important material for making electronic devices. Therefore, numerical simulation of semiconductor device problems is becoming more and more important. The mathematical models of semiconductor devices are considered. Matlab PDE toolbox can solve a series of problems semiconductor device simulation. Numerical simulation of the electric potential, electron concentration and the temperature distribution in the image can verify the semiconductor physical change in the situation. So the PDE toolbox has the advantages of simple operation and fast computation.
Keywords:Semiconductor, PDE Toolbox, Numerical Simulation
MATLAB PDE工具箱在半导体器件中的 应用研究
马宁*,王振宇,朱子君
中国石油大学(北京)理学院,北京

收稿日期:2019年4月29日;录用日期:2019年5月9日;发布日期:2019年5月16日

摘 要
半导体是近代发现的一种新型材料,其导电性能介于导体与绝缘体之间,并且导电性也会随温度变化,是制作电子器件的重要材料,因此半导体器件问题的数值模拟也越来越重要。本文主要研究用Matlab中PDE工具箱对瞬态半导体器件的数学模型进行求解,通过数值模拟得出其电子位势、电子浓度和温度分布数值解,并通过图像得到了半导体的物理变化情况,充分展现了PDE工具箱在求解过程中的操作简单、计算快等优点。
关键词 :半导体,PDE工具箱,数值模拟

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
半导体是近代发现的一种新型材料,其在常温下的导电性能介于导体与绝缘体之间,是制作电子器件的重要材料。半导体材料独特的导电性能为计算机和电子设备的发展提供了更加广阔的可能性,并且被广泛运用在日常生活之中。随着21世纪科学技术与经济的大幅发展,半导体的重要性有了极大的提升。在如今,大部分的电子产品中的核心器件,都与半导体有着密切联系。
对于半导体问题的数值方法研究已经成为一个重要的学科研究,吸引着国内外大量专家学者的探索研究。在二十世纪七十年代初,半导体器件就吸引了很多国外专家学者的研究,半导体器件模拟发展至今,国外已有很多优秀的模拟软件,如SEDAN、一维器件模拟程序NEMO (Nano Electronic Engineering Modeling),还有很多二维和三维半导体模拟软件以及一系列著名的商用器件模拟软件,它们在器件的数值模拟上都得到了广泛的应用 [1] 。由于国内半导体的应用发展较晚,目前许多国内著名高等院校和研究所都开始重视半导体器件模拟方面的研究工作,目前研究最多的模型便是热传导型半导体的瞬态问题 [2] [3] 并建立了模型库。
差分法和有限元方法是目前模拟半导体器件的主要方法。差分法是最早发展起来模拟半导体器件的,差分法比较简单,容易掌握,但对几何边界复杂的半导体器件,用多维差分法求解困难较大。有限元方法和差分法相比,相对区间的离散较自由,较容易处理边界复杂的半导体器件 [4] ,但需要自己编制程序并调试。正是由于边界条件的复杂性导致求解困难。目前应用Matlab工具箱可以解决数据处理、电动力学、非线性方程组等问题 [5] [6] [7] 。本文主要使用Matlab中PDE工具箱和编程相结合的方法求解瞬态半导体器件问题。算例表明使用PDE工具箱和编程相结合的方法求解,步骤简单,求解灵活,适应性强,结果可视化程度高。用此方法进行数值计算和图形处理,数值解与精确解误差较小,使用简单、方便、高效。
2. 半导体器件的数学模型
热传导型半导体瞬态问题的数学模型是由四个方程组成的非线性偏微分方程组的初边值问题所决定,设 是 中多边形或者多面体的Lipschitz区域,边界为 。考虑热传导型半导体的瞬态问题 [8] 。
(2.1)
(2.2)
(2.3)
(2.4)
(2.5)
(2.6)
其中(2.1)为电子位势方程,(2.2)和(2.3)分别为电子、空穴浓度方程,(2.4)为温度方程。电子位势方程是椭圆的,电子和空穴浓度方程是对流扩散型的,温度方程是热传导型的。电子位势是通过电场强度在电子、空穴浓度方程和热传导型温度方程中出现,并和相应的初边值条件构成封闭系统 [9] 。
3. PDE工具箱简介
MATLAB是用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言,自带强大的各种工具箱功能,其中偏微分方程工具箱(PDE Toolbox)本质可以看做一些M文件的集合,用户只要使用界面或M文件,画出所需要的求解区域,输入方程类型和有关系数,就可得到可视化结果 [10] 。
3.1. PDE工具箱求解的方程类型
工具箱有限元求解的基本思想是 [10] :通过将PDE求解区域三角形剖分;每个三角形上用二元线性函数做近似;选取二元线性函数的参数,使各个网格点满足PDE和边界条件 [11] 。
偏微分方程可根据它们的数学特征分为三大类型即椭圆型方程,抛物线型方程和双曲型方程 [12] [13] [14] [15] 。
椭圆型方程:
(3.1)
抛物型方程:
(3.2)
双曲型方程:
(3.3)
其中, 为平面有界区域, 为梯度算子,其中 是已知函数及u是未知函数。
3.2. 方程边界条件类型
边界条件有以下三类:
1) 狄利克雷(Dirichlet)条件
(3.4)
2) 诺依曼(Neumann)条件
(3.5)
3) 混合条件
上面两种条件的组合。
4. 半导体器件数学模型的求解
在研究半导体瞬态问题中,电子位势是椭圆型方程,电子、空穴浓度方程及为温度方程均为抛物型。使用PDE工具箱单独研究其数值解各种边界情况。
4.1. 半导体器件内电子位势变化模型
1) 考虑半导体电导率为 ,在定常电流下,电子位势V表示的Poisson方程:
假如以矩形介质中有两个圆,这两个圆均由半导体组成,其中一个保持电位为1,另一个为−1,电导率 矩形为边界满足Neumann条件 ,在使用PDE工具箱求解中,选择方程类型为椭圆型,取 ,外边界为Neumann条件 ,内边界均为Dirichlet条件,左圆取 ,右圆取 ,求解如图1所示。

Figure 1. Electron potential change model (1)
图1. 电子位势变化模型(1)
2) 假如一块圆形半导体器件中心挖去一正方形,外边界满足Neumann条件,内边界满足Dirichlet条件,考虑从 方向电流流入的电子位势方程定解问题模型下:
(外边界条件)
(内边界条件)
其中 ,求解时外边界选Neumann条件, ,内边界选Dirichlet条件, ,选择方程类型为椭圆型并取 ,剖分网格求解如图2所示:

Figure 2. Electron potential change model (2)
图2. 电子位势变化模型(2)
4.2. 半导体器件最小曲面的研究
半导体最小曲面的数学模型如下:
边界:
求解时,边界选择Dirichlet条件, ,选择方程类型为椭圆型剖分并求解,求解时在Solve Parameters选项中选用Use nonlinear solver (使用非线性求解器)得到图3数值解:
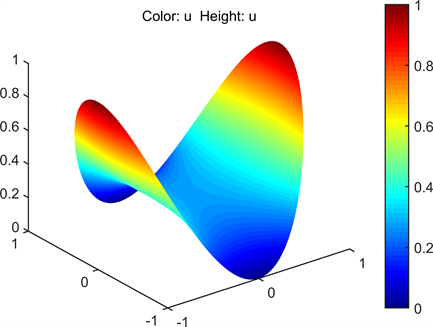
Figure 3. Numerical solution of minimal surface
图3. 最小曲面数值解
4.3. 半导体器件的热传导问题
1) 假设一长为L的匀质半导体柱形器件,其一端初始温度为20℃,一端与100℃恒温热源接触,其侧面与周围绝热的数值模型如下,讨论温度分布及热流变化情况。
热传导系数 ,比热容 , ,求解时方程类型选择抛物型并取 ,左右边界均为Dirichlet条件,左边界 ,右边界 得到数值解如下图4(a)~(c)。
 (a)
(a)
 (b)
(b)
 (c)
(c)
Figure 4. (a) Heat conduction model at t = 25; (b) at t = 100; (c) at t = 500
图4. (a) t = 25热传导模型;(b) t = 100热传导模型;(c) t = 500热传导模型
由以上可以看出,在t为25时,其两端温度差别大,中间温度差别较小,当t为100时,其不同位置的温度差异缩小,但温度分布仍未曲面,当t为越来越大时,温度分布变成平面并不在随时间变化,说明温度分布达到稳定梯度。
2) 环境向半导体内部的热量传递也为抛物型模型,数学模型为:
假设一个方形区域,导热系数为10,密度为2,在其中有一菱形半导体热源为4,导热系数为2,密度为1,两者的比热容为0.1。用PDE工具箱求解时选择Heat Transfer(热传导)模型并选择方程类型为抛物型并在对应区域输入相应密度,比热容,导热系数等,所有边界条件选择Dirchlet,求得0.1时刻的温度T的分布如图5。

Figure 5. Heat conduction model (2)
图5. 热传导模型(2)
4.4. 半导体器件电子浓度变化模型
一个带圆形孔的板状半导体器件的电子浓度变化问题,其左边保持浓度为100,电子从右边向环境空气定常流动,其他边及内孔边缘保持绝缘,初始 的浓度为0,可以看做以下定解问题
(左边界条件)
(右边界条件)
(其他边界条件)
求解时方程类型选择抛物型,并取 ,其中左边界为Dirchlet条件 ,右边界Neumann条件 ,其他边界 ,得到数值解如图6(a)、图6(b)所示。
 (a)
(a) (b)
(b)
Figure 6. (a) Electron potential change 2D graph; (b) Electron potential change 3D graph
图6. (a) 电子浓度变化平面图;(b) 电子浓度变化三维图
5. 结论
论文通过对半导体器件的数学模型问题的研究,结合半导体器件中的电子位势变化、电子浓度变化、温度变化、最小曲面等数学模型,使用Matlab PDE工具箱对其模拟计算,得到电子位势、电子浓度的变化图像、温度场的分布图像和最小曲面的数值结果。研究发现通过PDE工具箱计算不仅方便快捷,而且强大的图形可视化功能使计算结果更加形象。
基金项目
中国石油大学(北京)青年骨干教师项目资助。
文章引用
马 宁,王振宇,朱子君. MATLAB PDE工具箱在半导体器件中的应用研究
Application Research of MATLAB PDE Toolbox in Semiconductor Device[J]. 计算机科学与应用, 2019, 09(05): 874-822. https://doi.org/10.12677/CSA.2019.95098
参考文献
- 1. 杨志伟. 一类半导体模型的几种数值方法比较[D]: [硕士学位论文]. 济南: 山东大学, 2014.
- 2. 刘影. 半导体器件的二维数值模拟[D]: [硕士学位论文]. 成都: 电子科技大学, 2015.
- 3. 丁红梅. 基于有限体积法的半导体器件数值模拟[D]: [硕士学位论文]. 成都: 电子科技大学, 2012.
- 4. 李文学. 电场数值计算的常用方法[J]. 山东工业技术, 2014(22): 282.
- 5. 王文东, 武海妮, 吴强, 包曾. 基于Matlab的非线性方程组求解[J]. 信息与电脑(理论版), 2018(15): 36-38.
- 6. 李奇. Matlab智能算法工具箱在数据处理方面的应用[J]. 电脑编程技巧与维护, 2018(7): 120-122.
- 7. 刘思平. Matlab PDE工具箱在电动力学教学中的辅助应用[J]. 廊坊师范学院学报(自然科学版), 2017, 17(1): 110-112.
- 8. 袁益让. 半导体瞬态问题计算方法的新进展[J]. 计算物理, 2009, 26(3): 317-324.
- 9. 杨青. 半导体瞬态问题的修正迎风有限体积格式[J]. 系统科学与数学, 2008(6): 725-738.
- 10. 黄作英, 阙沛文, 陈亮. PDE工具箱实现偏微分方程的有限元求解[J]. 计算机仿真, 2006, 23(9): 100-102.
- 11. 李萍, 张磊, 王垚廷. 基于Matlab的偏微分方程数值计算[J]. 齐鲁工业大学学报, 2017, 31(4): 39-43.
- 12. 宋克志, 刘智儒. 基于Matlab语言的有限元法及其应用[J]. 烟台师范学院学报(自然科学版), 2004, 20(2): 100-102.
- 13. 冯桂莲. 偏微分方程的MATLAB数值解法及可视化[J]. 计算机技术与发展, 2013(12): 120-123.
- 14. 李明. 偏微分方程的MATLAB解法[J]. 湖南农机, 2010(5): 89-91.
- 15. 冯桂莲. 有限元数值解法在MATLAB中的实现及可视化[J]. 软件工程师, 2015(1): 61-64.
NOTES
*通讯作者。