Hans Journal of Data Mining
Vol.
09
No.
02
(
2019
), Article ID:
29878
,
8
pages
10.12677/HJDM.2019.92007
Five Understandings on Support Vector Machine Regression
Lingchun Xiong, Yumei Li
School of Science, Beijing Technology and Business University, Beijing
Received: Apr. 4th, 2019; accepted: Apr. 18th, 2019; published: Apr. 25th, 2019

ABSTRACT
There are differences between support vector machine regression and classification. The problem of classification starts with maximizing the gap between the two classes, but regression problem needs to find a regression equation which is close to the real function value. In addition, support vector machine regression and ordinary regression problems are different; it needs to set up a interval belt, and the losses are not calculated for the data in the interval belt, but the losses must be calculated for the data beyond belt. While minimizing losses, there is another item in the objective function of the model, and the understanding of this item brings difficulties in the teaching process. Especially after studying the SVM classification problem, it is easier to associate this term with the maximization interval of the same term in the classification problem but it cannot be directly matched. From regularization, structural risk minimization, flatteness of the regression hyperplane, transformation of regression problem to binary classification problem, and the nature of regression, we will analyze and explain in different points, and clear up the obstacles for support vector regression’s understanding. Moreover, the fifth viewpoint is at a new height, unifies the first four understandings from the nature of the problem, and it also has its own unique views.
Keywords:Support Vector Machine Regression, Five Understanding of Objective Function, Regularization, Structural Risk Minimization, Flatteness of the Regression Hyperplane, Transformation of Regression Problem to Binary Classification Problem, The Nature of Regression

支持向量机回归模型中目标函数的 五个理解
熊令纯,李裕梅
北京工商大学理学院,北京
收稿日期:2019年4月4日;录用日期:2019年4月18日;发布日期:2019年4月25日

摘 要
支持向量机回归和支持向量机分类有区别,分类问题主要从最大化两类间的间隔入手,而回归问题则需要寻找适合这批数据的自变量和因变量之间关系的回归方程,使得由回归方程计算出来的因变量值和实际数据中的因变量值尽量接近。并且,支持向量机回归和普通的回归问题还不一样,设定了一个 间隔带,在这个间隔带内的数据点、不计算损失,之外的计算损失,在尽量最小化损失的同时,模型的目标函数里多了个 ,关于这个项,有很多疑问,给支持向量机回归目标函数的理解造成了很大的困难,尤其是在学习了支持向量机分类问题后,更容易把这个项和分类问题中同样的项意味着的最大化间隔相联系,但又不能直接对应上。于是,我们从正则化、结构风险最小化(岭回归、权重衰减)、回归超平面的flatten、二分类问题的转化、回归问题的本质这五个方面着手,从不同的角度进行透彻分析和解释 ,从而为支持向量机回归模型的目标函数的理解进一步理清思路、扫清障碍。而且,第五个理解站在了新的高度,从问题的本质出发,统一了前面四个理解,也具有自己独特的看法。
关键词 :支持向量机回归,目标函数的五个理解,正则化,结构风险最小化,回归超平面的Flatten, 二分类问题的转化,回归问题的本质

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 支持向量机回归的一般形式
设样本为 。一般的回归,就是计算真实的y值与回归超平面 计算的函数值 之间的差距,使得这些差距平方和最小的情况下找到 表
达式中的参数W和b,从而求得回归方程。
支持向量机回归最早是在1996年由Vladimir N. Vapnik等人提出 [1] 。在SVM回归过程中,首先,通过函数映射 把数据转换到高维空间去找一条回归直线或者回归超平面。然后,为回归直线或超平面构造 的间隔带,在间隔带内的数据点,认为没有损失,在间隔带外的才计算损失。如下图1,为每个数据点设两个损失量,即,如果该数据点在间隔带上方,损失记为 ,在下方,则损失记为 ,这两个损失量最多只能有一个成立,或者说最多只有一个非零,因为这个数据点要么在回归超平面的上方,
要么在下方;如果恰好在边界 或者 上,则 和 都为0,
这样的数据点就是支持向量。
SVM回归的数学模型的一般形式如下 [2] [3] [4] [5] :
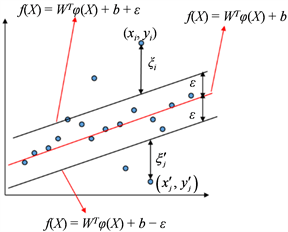
Figure 1. interval bands of SVM regression
图1. SVM回归的 间隔带
其求解过程和支持向量机分类问题的求解类似,也是用拉格朗日乘子法,即,让每个约束条件乘上一个拉格朗日乘子再带入目标函数中,得到下面的拉格朗日函数 :
和 是拉格朗日乘子,并且所有拉格朗日乘子都要求大于或等于0。然后通过 函数对W和b求偏导等于0,得到:
将上面4个结果带入拉格朗日函数中,经过整理,得到:
从而得到对偶问题:
然后用SMO算法求得权重:
再根据各个支持向量满足的条件 ,求得b,并将求得的多个b做平均,得到最终的截距 . 从而得到最终回归超平面为:
,
其中,K为核函数,在一般的计算机软件里经常有以下几种:
线性核函数:
多项式核函数:
径向基核函数(或者叫高斯核函数):
sigmoid核函数:
2. 支持向量机回归中目标函数的五大理解
支持向量机回归模型的目标函数中,为什么还有 (即 ),和支持向量机分类问题的最大化间隔有关系么?因为支持向量机分类的目标函数里也有 ,是通过最大化间隔推导出来的。有的
文献 [3] [4] [5] [6] 里关于这个项,讨论了W的正则化;有的文献 [7] 讨论了回归直线或超平面的flatten,
还有的文献 [8] 把回归转换成二分类问题来得到 这个项。针对SVM回归的目标函数
究竟还有多少疑问?还可以从哪些方面来理解?
接下来,我们就从支持向量机分类中的最大化间隔、机器学习中的正则化、结构风险的最小化和回
归超平面的flatten这几个方面来对 的各种理解进行分析.其中,前四个方面是通过大量研读文献,
进行的融会贯通、进一步总结和提升;第五个方面,是我们通过自己独立的深入思考,对该问题进行的透彻的理解和分析,从而实现了对支持向量机回归的比较全面的解析,站在回归问题本质的高度,看到了前面四个理解在其中的体现和统一。
1) 从正则化的角度看
回归,目的是希望真实函数值和回归方程预测的函数值之间的差距最小,在支持向量机回归中,有一个 误差带,二者的差距在这个误差带以内,就不计损失,如果在这个之外就计算损失,且相应损失
记为 和 ,于是,追求损失和 的最小。得到支持向量机回归的模型如下:
.
然后,为了问题求解过程的简化、得到比较好的解和防止过拟合或者叫增强泛化性,在目标函数中
引入正则项 [9] 一起进行最小化,从而把W参数限制在一个很小的范围内,如下图2,回归问题
的求解最终与W正则化的小范围圆圈边界相交,这个交点就是回归问题的关于W的解。这样,W的各个分量很小以后,当数据点的特征属性值X带入回归方程 ,W因为值很小对f(X)的影响小,那么f(X)的值主要由数据属性值X来决定,从而不会因为训练样本计算出来的W起决定作用,即防止了过拟合,同时也简化了求解范围。
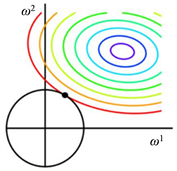
Figure 2. The solution after adding regularization
图2. 加了 正则化以后的求解情况
正则化以后的求解情况
这样,得到支持向量机回归的最终模型为 [3] [4] [5]
这种加正则项的方法,叫着Tikhonov正则化,在统计学中称为岭回归(ridge regression),在机器学习中称为权重衰减(weight decay) [6] 。
2) 从结构风险最小化看 [10] [11]
经验风险最小化(Empirical Risk Minization, ERM) [9],其中的经验风险,即经验误差,也就是训练误差。结构风险最小化(Structure Risk Minization, SRM),基本思想是在追求经验误差最小化的同时,使学习器在整个样本集上总的期望风险得到控制 [10],于是,通过加正则项来实现对测试样本泛化性,如下面公式,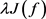 是加的正则项,
是经验风险。
是加的正则项,
是经验风险。
对于支持向量机, ,加正则项就是 ,于是得到目标函数:
,
C用于调节正则项和损失计算之间的重要性,最后的支持向量机回归模型为
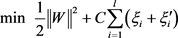
.
实际上,这里的经验风险最小化,就相当于(1)中的计算 间隔带以外的损失,然后再加正则项,这和(1)中的理解统一起来了。
3) 从回归超平面的flatten来看
为了找到对于训练样本最多有 偏差的回归超平面 ,这个函数 必须尽可能的flatten [7],这就要求最小化 ,写成凸优化问题的形式,得到支持向量机的模型如下
再者, 之外的损失 和 要最小化,于是在目标函数里加入 ,得到最终模型如下
实际上,这里要求回归直线或超平面的flatten,“扁平”,就是要求W的要扁平,即 尽量小,这又和前两个理解统一了!
4) 从二分类问题的转化来看
把每一个数据点 变成两个数据点 和 ,从而构造出新的训练集
新构造出来的这个训练集的样本点是两个类,从而构造分类超平面把这两类样本分开,那么这个超平面就是所求的回归面,模型如下 [12] :
这里的权重比分类问题多了一个关于y的权重 。
设 为上面问题的最优解,若令 ,并考虑下面问题
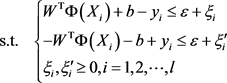
则该问题的解 满足 [8] 。上面这个模型就是文献 [12] 中描述的推广的最大化间隔法得到的支持向量机回归模型,这和前面几个理解得到的模型在损失惩罚项那里多了个 ,但并
不影响目标函数的最小化。
5) 从回归问题的本质来看
首先是要最小化 带状区域外的损失 和 ,所以有 。最小化这个损失,就会把回
归超平面置于数据点中心位置去,使得尽量多的数据点距离回归超平面最近,或者是使得这些数据点尽量落在在这个上下(即竖直)方向的 差距范围内;再追求带状区域边界两条虚线之间的距离或者叫间隔最大,即下图3中的ρ或者Margin最大(这就和前面第四点的二分类问题看法相统一),就可以使得更多的样本点“落入”这个带状区域、这样来尽量最小化损失,且使得距离回归面 最远的样本点距离回归面尽量再近一些,从而使得泛化性能更好(这就和前面第一点和第二点的正则项和经验风险的看法一致)。

Figure 3. The Margin of SVM regression
图3. SVM回归的Margin
那么,这个Margin的最大化,和支持向量机分类里的最大化Margin一样,使得 最大化,从而使得 最小化(这就和前面第三点的“flatten”的理解相统一)。这种“把回归面拉到数据点中间去,再最大化Margin”的思想,综合起来就得到支持向量机回归的目标函数 ,于是
得到最终的模型如下
这一点的理解,将一般回归问题计算的损失和支持向量机二分类问题特有的观点统一到支持向量机回归模型中,最小化损失,使得回归面回到数据点的中心位置,再通过SVM特有的二分类最大化间隔使得尽量多的数据点落在 带状区域内、从而进一步减少带状区域外要计算的损失!
3. 结论
对于支持向量机回归的目标函数中的 项,本文从正则化、结构风险最小化(最终论证成“岭回
归”或“权重衰减”)、回归超平面的flatten、二分类问题的转化、回归问题的本质等五个方面进行了剖析和理解。前四个方面是通过大量研读文献和分析,进行的融会贯通、总结和提升,最后一个方面(回归的本质)的理解是经过作者们的深入思考而来,站在了一个新的高度,看到了前面四个理解的影子,是所有理解的统一。希望这些不同角度的理解给支持向量机回归的教学带来很好的认识和帮助,同时为这方面的科研提供更丰富的内涵。
文章引用
熊令纯,李裕梅. 支持向量机回归模型中目标函数的五个理解
Five Understandings on Support Vector Machine Regression[J]. 数据挖掘, 2019, 09(02): 52-59. https://doi.org/10.12677/HJDM.2019.92007
参考文献
- 1. Drucker, H., Burges, C.J.C., Kaufman, L., Smola, A.J. and Vapnik, V.N. (1997) Support Vector Regression Machines. Advances in Neural Information Processing Systems, 9, 155-161.
- 2. 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.
- 3. Bishop, C.M. (2006) Pattern Recognition and Machine Learning. Springer, New York.
- 4. Nielsen, M.A. (2015) Neural Networks and Deep Learning. Determination Press. http://neuralnetworksanddeeplearning.com/
- 5. Sergios Theodoridis, Konstantinos Koutroumbas, 著. 模式识别[M]. 第四版, 李晶皎, 等, 译. 北京: 电子工业出版社, 2016.
- 6. https://en.wikipedia.org/wiki/Tikhonov_regularization
- 7. Smola, A.J. and Schölkopf, B. (2003) A Tutorial on Support Vector Regression.
- 8. 邓乃扬, 田英杰. 数据挖掘中的新方法——支持向量机[M]. 北京: 科学出版社, 2004.
- 9. Drucker, H., Burges, C.J.C., Kaufinan, L., et al. (1997) Support Vector Regression Machines. Advances in Neural Information Processing Systems, 9, 155-161.
- 10. https://en.wikipedia.org/wiki/Support_vector_machine#Empirical_risk_minimization
- 11. Vapnik, V.N. (1999) The Nature of Statistical Learning Theory: Statistics for Engineering and Information Science. 2nd Edition, Springer-Verlag, New York. https://doi.org/10.1007/978-1-4757-3264-1
- 12. 李洋. Matlab技术论坛[EB/OL]. http://www.matlabsky.com