Journal of Water Resources Research
Vol.
08
No.
03
(
2019
), Article ID:
30659
,
12
pages
10.12677/JWRR.2019.83030
A Short-Term Optimal Scheduling Model of Cascaded Hydropower Stations with One Reservoir Considering the Effect of Backwater
Han Gao, Jianjian Shen*, Chengguo Su, Chuntian Cheng, Xinyu Wu
Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian Liaoning

Received: May 6th, 2019; accepted: May 24th, 2019; published: Jun. 5th, 2019

ABSTRACT
The hydraulic coupling among cascaded hydropower stations with one reservoir is close, and the backwater from the downstream reservoir is easy to form a jacking effect on the tailwater level of the upstream reservoir, which affects the generation efficiency and planning. Based on the unit of the basic dispatching unit, this paper puts forward a short-term optimal scheduling model of cascaded hydropower stations with one reservoir, which takes the effect of backwater into consideration. Through the interval division of the downstream reservoir water level, the three-dimensional curve of tailwater level-discharge-reservoir water level is described as three typical scenarios, and the linear description is realized by piecewise linear method. The developed model converts into a mixed integer linear programming model, which can be solved by commercial software Lingo. Based on a case study with Tianshengqiao cascaded hydropower stations located in Hongshui River, the study shows that the proposed model considering backwater effect can realize the refined calculation and improve the economic benefits of scheduling.
Keywords:Cascaded Hydropower Stations with One Reservoir, Backwater, MILP
考虑回水效应的一库多级式水电站群 短期优化调度模型
高寒,申建建*,苏承国,程春田,武新宇
大连理工大学建设工程学部,辽宁 大连

收稿日期:2019年5月6日;录用日期:2019年5月24日;发布日期:2019年6月5日

摘 要
“一库多级”梯级水电站间水力联系紧密,下库易产生回水对上库尾水位形成顶托作用,影响发电效率及计划安排。本文以机组为基本调度单元,提出了考虑回水效应的“一库多级”式水电站群短期优化调度模型,通过对下游库水位进行区间划分,将尾水位–泄量–库水位三维曲线描述为三种典型情境,采用分段线性方法实现了线性描述,最终将原问题转换为混合整数线性规划模型,并利用商用软件Lingo进行求解。经红水河干流天生桥梯级水电站群实例验证,提出的模型可在充分考虑回水影响下实现水电站群的精细化计算,有效提高梯级水电站群的发电量。
关键词 :一库多级,回水效应,混合整数线性规划

Copyright © 2019 by author(s) and Wuhan University.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
西南地区是我国水电资源最丰富的地区 [1] ,经过多年的开发建设,“一库多级”或“多库多级”式调度已成为西南流域梯级电站普遍的运行方式 [2]。这些梯级库群以大库容、强调节能力的大型电站为龙头,下游有1至多座小库容、高水头、弱调节能力的水电站为附属,利用龙头水库的调蓄作用,最大化梯级电站间的补偿能力,以提高整个梯级的水能利用率。与传统梯级库群中有多个季调节能力以上的电站不同,由于调节能力的巨大差异,“一库多级”式梯级电站间的水力联系往往更加紧密。具体表现为:1) 存在流量敏感性电站,由于库容的限制,下游水库的水位极易受到上游龙头电站下泄流量变化的影响;2) 存在回水效应,部分下游电站和龙头电站之间的距离过近,流至下库的水流易产生回水,对上库尾水位形成顶托作用,从而影响上库的发电水头。上述两点极大地加剧“一库多级”式梯级短期发电计划编制的难度,使得针对其开展短期优化调度研究具有重要意义。
现有的梯级电站短期优化调度多以电站为基本单元进行研究 [3] [4] [5] [6] ,这样虽然在一定程度上简化了模型,但是对于机组振动区、启停持续时间、开停机次数等约束缺乏精细化考虑,导致模型所求解运用于工程实际时需要做出一定的修正。文献 [7] 提出了一种考虑机组组合的梯级水电短期调度模型,着重于模型中非线性因素的线性化转换,但在处理梯级水力联系时,只简单地运用尾水位泄量二维曲线计算上游尾水位,忽略了梯级间的回水效应,使得模型运用于实际时可能存在一定的水头误差,从而影响下游电站的调度。文献 [8] 通过拟合泄量和发电水头的关系,提出了一种尾水位的经验计算方法。相较于水量平衡方程构建出梯级水库间的水量联系,尾水位–泄量–库水位三维曲线构建了上下游水库间的水头联系,更贴近实际运行工况。引入尾水位–泄量–库水位三维曲线,可以有效提高模型的计算精度。
以机组为单元,考虑回水效应的梯级短期优化调度是一个典型的混合整数非线性规划(MINLP)问题。动态规划及其改进算法 [9] [10] [11] 、智能算法 [6] 等常规的算法在求解该问题时,往往会遇到难以求得最优解或陷入“维数灾”等难题。文献 [12] 提出了考虑水头敏感性的梯级水电短期MINLP模型,通过建立发电水头和出力、库容、出库流量的线性关系,简化了模型,但简化后的模型普适性有所降低,难以运用于其他梯级库群。
随着商业软件的发展,混合整数线性规划MILP已成功地应用于解决水电短期优化调度问题 [13] [14] [15]。相较于MINLP模型求解时容易陷入局部最优,MILP模型不仅可求得全局最优解,在时效性上也要略胜于MINLP模型。基于“一库多级”水电站群的强水头联系,本文在前人研究的基础上,以发电量最大为目标,引入尾水位–泄量–库水位三维曲线,提出了考虑回水效应的“一库多级”式水电站群短期优化调度模型,通过对下游库水位进行区间划分,将尾水位–泄量–库水位三维曲线描述为三种典型情境,采用分段线性方法实现了线性描述,最终将原问题转换为混合整数线性规划模型,并利用商用软件Lingo进行求解。以红水河干流天生桥梯级10台机组为例验证了所提模型的有效性。
2. 模型描述
2.1. 目标函数
梯级水电站群的短期优化调度主要有两种模式:“以水定电”和“以电定水”。针对前者主要有梯级发电量最大模型、梯级发电效益最大模型等,后者有梯级总耗水量最小模型、梯级蓄能最大模型等。在已知梯级来水的情况下,为了最大限度地发挥水电经济效益,选取调度周期内梯级水电站总发电量最大为目标函数,表示如下:
(1)
式中:E为调度期内水电站群的总发电量,MW h;t为调度时段,h;T为调度时段总数,文中取1 d;i为电站编号,I为参与调度的梯级电站总数;n为机组编号, 为电站i的机组数目; 为时段t时电站i的机组n的出力,MW; 为调度时段步长,文中取1 h。
2.2.约束条件
梯级水电站群的短期优化调度涉及的约束数目多且部分难于直接处理,可将其划分为两类,线性约束和非线性约束。
1、线性约束
1) 水量平衡约束
(2)
(3)
式中: 为水库i在t时段末的库容,m3; 为水库i在t时段的入库流量,m3/s; 为t时段水库 和水库i的区间流量,m3/s; 为水库i在t时段的出库流量,包括调度周期内电站的发电流量和弃水流量,m3/s; 为电站i的机组n在t时段的发电流量,m3/s; 为电站i在t时段的弃水流量,m3/s; 为调度时段步长,h。
2) 始、末库容限制
(4)
(5)
式中: 、 分别为水库i在给定调度期初的库容值和调度期末的库容控制值,m3。
3) 水库边界条件
(6)
(7)
(8)
式中: 、、 分别为水库i在t时段末的库容及其上、下限,m; 、 分别为水库i的出库流量上、下限,m3/s; 为水库i的弃水流量上限,m3/s。
4) 机组出力限制
(9)
式中: 、 分别为机组n的出力上、下限,MW; 为电站i的机组n在t时段运行状态变量, 表示机组处于开机运行状态,否则 。
5) 机组发电流量限制
(10)
式中: 、 分别为电站i的机组n的发电流量上、下限,m3/s。
6) 机组开、停机状态约束
(11)
(12)
(13)
式中: 为电站i的机组n在t时段的开机操作变量, 表示机组n在从 时段到t时段进行了开机操作,否则 ; 为电站i的机组n在t时段的关机操作变量 , 表示机组n在从 时段到t时段进行了停机操作,否则 。
7) 机组开、停机持续时间约束及最大开机次数约束
(14)
(15)
(16)
式中: 、 分别为机组n最小开、停机持续时间,h; 为机组n在调度期内的开机次数上限。
8) 机组发电水头约束
(17)
式中: 为电站i的机组n在t时段的发电净水头,m; 为水库i在t时段末的坝前水位,m; 为电站i在t时段末的尾水位,m; 为电站i的机组n在t时段的水头损失值,m。
2、非线性约束
1) 水位库容约束
(18)
式中: 为水库i的水位库容关系函数。
2) 尾水位泄量约束
(19)
式中: 为水库i的尾水位、水库i出库流量和水库 的坝前水位之间的关系函数。
3) 机组动力特性约束
(20)
式中: 为电站i的机组n的出力与发电流量、发电水头之间的关系函数。
4) 机组振动区限制
(21)
式中: 、 分别为电站i的机组n的第k个振动区的上、下限,MW。
3. 求解算法
由于上述已构建模型中的线性化约束(式(2)~式(17))无需另加处理,所以原模型的求解难点是对于非线性约束(式(18)~式(21))的处理。如何在保证精度的前提下,对这些非线性因素进行线性化处理,从而构建MILP模型,是本文求解算法的关键所在。
3.1. 水位库容约束处理
水位库容曲线表征了水库水位与库容之间的非线性关系,是水库调度的重要依据。本文通过对库容进行离散实现其线性化处理。具体方法如下:
将水库i的库容进行离散,共分为A个区间,离散后的水位值表示为:
(22)
式中: 、 分别为水库i的第a个插值点及其所对应水位值。
则水库i在t时段的库容可表示如下:
(23)
(24)
(25)
(26)
式中: 为水库i在t时段的库容离散区间指示变量,当 时,表示此时水库i在t时段的库容位于第a个库容区间内,否则 。
则水库i在t时段的水位可表示如下:
(27)
运用上述式(23)~(27)即可实现对水库水位库容曲线的分段线性逼近。需指出的是,对于一库多级式梯级电站中的龙头电站,其调节能力通常在季调节及以上,而短期调度的调度周期通常为1 d,因而其水位库容在调度周期内通常波动较小。因此,对于龙头电站,只需在初始水位附近进行分段线性逼近即可,此举既可简化计算,又可达到计算所需的精度要求。
3.2. 尾水位泄量约束处理
尾水位–泄量–库水位三维曲线(如图1所示)描述了在已知下游水库坝前水位的情况下,不同下泄流量对应的上游水库的尾水位情况,表征了下游水库坝前水位、上游水库下泄流量和尾水位之间的非线性关系。利用尾水位泄量曲线,可以建立梯级水库间的水头联系。在线性化模型求解中,选择合适的尾水位泄量曲线并对其进行合理的线性化显得尤为重要。
本文尾水位–泄量–库水位三维曲线线性化共分为三步:第一步,预估下游水库坝前水位的变化区间,并将其离散为3个连续的子区间;第二步,选定每个水位子区间内具有代表性的尾水位泄量曲线,并与下游水库库水位关联;第三步,对选定的尾水位泄量曲线进行分段线性处理,从而实现原三维曲线的线性化。
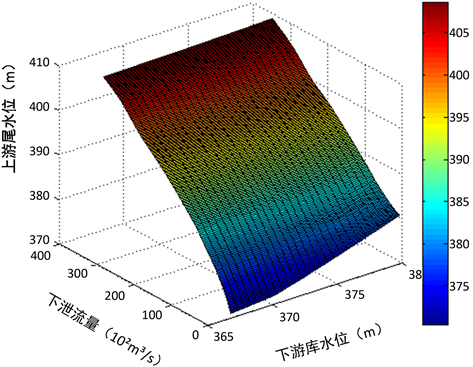
Figure 1. Three-dimensional curves of tail water level - discharge - reservoir water level
图1. 尾水位–泄量–库水位三维曲线
3.2.1. 下游水库库水位离散
根据已有的水库历史运行资料,并结合工程经验,预估下游水库 的水位变动区间,记为 。将该区间离散为3个连续的子区间 、 和 (如图2所示),其中 ,。那么对于水库 在任何时段内的水位必然满足以下约束:
(28)
式中: 为下游水库 在t时段的水位离散区间指示变量,当 时,表示此时水库 在t时段的水位位于第k个水位区间内,否则 。
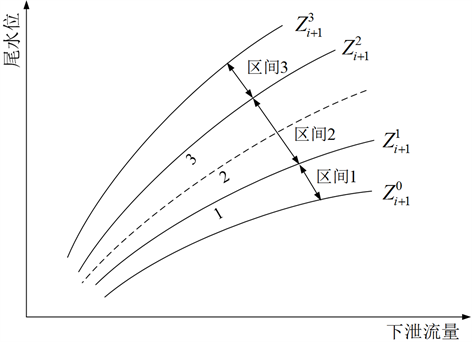
Figure 2. Simplified curves of tail water level-discharge-reservoir water level
图2. 简化尾水位泄量曲线
3.2.2. 下游水库坝前水位关联尾水位泄量曲线
在下游水库坝前水位变化的3个区间内,分别选择一条特定的尾水位泄量曲线,来表征该区间下的水位所对应的所有的曲线,从而实现下游水库坝前水位与上游水库尾水位泄量曲线的关联。此时,上游水库尾水位的变化只有水库的出库流量有关,与下游水库的坝前水位无关,即实现了上游水库尾水位、下泄流量和下游水库坝前水位之间三维关系的二维转化。依据上述思路,构建上游水库尾水位泄量曲线和下游水库坝前水库关联的数学表达:
(29)
(30)
(31)
式中: 为第b个下游水库坝前水位子区间内上游水库尾水位与下泄流量的函数关系。
由式(28)可知,当下游水库坝前水位处于某个子区间时,有且只有一个 ,则式(29)~式(31)中只有一个公式得以成立,其他两项约束式相应会被松弛,可得有且只有一个b使得 ,即只有一条尾水位泄量曲线被选中,从而实现下游水库坝前水位与尾水位泄量曲线的关联。
3.2.3. 尾水位泄量曲线线性化转换
3.2.2节中被选定的尾水位泄量二维曲线仍然为非线性曲线,不可直接运用到MILP模型中参与计算。参考3.1节中水位库容约束的处理方法,离散下泄流量,线性插值得到相应的尾水位,实现尾水位泄量曲线的线性处理。详细步骤此处不再赘述。
3.3. 机组动力特性约束处理
机组动力特性曲线描述的是机组的出力与发电流量、发电水头之间的三维关系。其处理方法可参考3.2节中尾水位泄量约束的线性化处理。即第一步,预估发电水头的变化区间,并将其离散为多个连续的子区间;第二步,选定每个水头子区间内具有代表性的机组动力特性曲线,并与发电水头相关联;第三步,对选定的机组动力特性曲线进行分段线性处理,从而实现原三维曲线的线性化。详细步骤此处不再赘述。
3.4. 机组振动区限制处理
水电站发电机组的振动区又称限制运行区,机组出力需避免落入此区域内,因而机组出力的可运行区域就被振动区划分为多个不连续的区间,称为机组的安全运行区。考虑机组出力的上下限,K个振动区便将机组划分为 个安全运行区,据此机组振动区限制式(21)可转化如下:
(32)
式中: 为指示变量, 表示电站i的机组n在t时段的出力位于第k个安全运行区; 、 分别为电站i的机组n的第k个安全运行区的上、下限,且有 ,。
4. 应用实例
4.1. 工程背景
位于红水河上游南盘江的天生桥一级和二级电站是典型的“一库两级”梯级水电站群,天生桥一级电站作为南盘江龙头电站,具有不完全多年调节性,其调节库容是下游天生桥二级的700余倍。两座电站仅相距6.5 km,水头联系紧密,一级电站的下泄流量流至二级坝前时,极易向上游反流,下游顶托作用显著,增加了梯级短期优化调度的难度。本文以天生桥梯级10台机组为例验证所提MILP模型的有效性,并调用LINGO商业软件包进行模型求解。天生桥一级和二级电站特性如表1所示。
Table 1. Characteristic parameters of cascaded hydropower plants
表1. 梯级电站主要特征参数
4.2. 计算结果及分析
分别选取汛期(2018年8月)和枯期(2018年11月)某一日来水数据,以1 h为计算步长,1 d为调度周期,进行验证。考虑到工程实际中不希望弃水现象的发生,故而在计算中将各时段的弃水量设置为0。MILP模型的求解速度与二进制整数变量的个数密切相关,因本文重点解决回水问题,且天生桥一级在日调度周期内水头变幅很小,故在处理振动区约束方面,将天生桥一级原水头关联的可变振动区处理为恒定水头下的固定振动区,以此减少二进制整数变量的使用,从而加快模型的求解速度。为了进一步提高计算效率和精度,根据已知的电站始末水位和入库流量,推导出天生桥一级和二级电站日内发电水头变化区间分别为[123, 131]和[198, 203],在此区间内进行机组动力特性曲线的线性化处理。
图3为优化调度计算得到的汛期天一、天二的出力和水位变化过程图。对于大库容、强调节能力的龙头电站天一,汛期其水位日变幅仅有0.16 m,波动很小。而受自身调节能力和流量敏感特性的影响,天二水位日变幅高达8 m,且在调度期均处于满发状态,前期为增大出力,水位呈下降趋势,后期为下一周期电站运行考虑,开始蓄水抬高水位。此外,汛期虽然来水丰富,但是天二调节能力有限,天一的出力受阻,为了保证天二不会出现弃水,天一只能不断蓄水,因此水位呈现出单调上涨的趋势。
 (a) 天生桥一级
(a) 天生桥一级
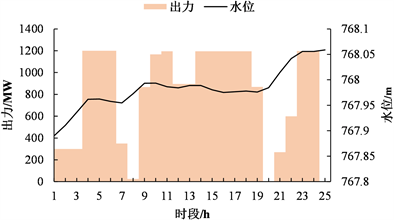 (b) 天生桥二级
(b) 天生桥二级
Figure 3. Power output and water level of hydropower plants in flood season
图3. 汛期电站出力及水位变化过程
图4为优化计算得到的汛期部分机组出力过程。由表1可知,天一4台机组型号相同,天二6台机组也相同,故各自只列出一个机组作为代表。由图4可知,两台机组调度期内的出力均有效避开了振动区,且机组未出现频繁启停的情况,满足了模型中所设置的机组开、停机持续时间及最大开机次数约束,保证了机组的稳定运行,可见优化结果具有合理性。
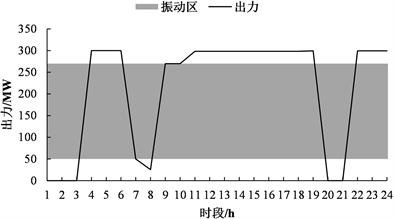 (a) 天生桥一级1#机组
(a) 天生桥一级1#机组
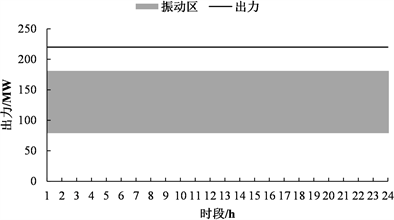 (b) 天生桥二级1#机组
(b) 天生桥二级1#机组
Figure 4. Power output of units in flood season
图4. 汛期部分机组出力过程
4.2.2. 枯期计算结果分析
图5为优化调度计算得到的枯期天一、天二的出力和水位变化过程图。值得注意的一点是:在枯水期,天二仍是满发出力状态。究其原因,主要是天二虽然装机容量很大,但是由于库容的限制,只能将来水全部用来发电,以此减少弃水。从水位变幅来看,由于枯期来水偏少,不能满足运行需求,天一只能不断放出库容,以此满足发电量最大的目标,因此水位呈不断下降的趋势;天二前期在上游来水不足的情况下,利用水位降幅提高发电量,后期利用天一下泄的库容提高水位,为下一调度周期做准备。
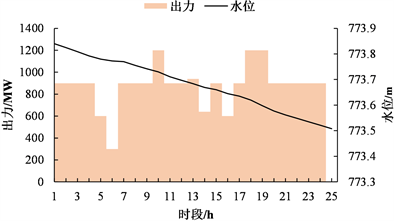 (a) 天生桥一级
(a) 天生桥一级
 (b) 天生桥二级
(b) 天生桥二级
Figure 5. Power output and water level of hydropower plants in dry season
图5. 枯期电站出力及水位变化过程
4.2.3. 考虑回水与未考虑回水模型尾水位对比分析
未考虑回水效应的模型常将尾水位泄量曲线处理为二维曲线,不与下游库水位相关联。为了更合理地进行对比分析,提取本文所提模型汛期计算结果中的天生桥一级24个时段的泄量数据,对天生桥一级的二维尾水位泄量曲线进行分段线性处理,得到未考虑回水效应情况下的尾水位数据,如图6所示。
由图6可知,两者尾水位数据相差较大,考虑回水效应模型所得的尾水位要明显高于未考虑回水效应的模型。究其原因,是天一的下泄流量流至天二之后产生回水,对天一的尾水位形成顶托作用,从而抬高了天一的尾水位。正面证明了本文所提模型对于回水问题处理的有效性。
如果忽略回水问题,计算所得的天一尾水位将远低于实际,发电水头远高于实际,间接导致计算所得的发电量偏高,影响工程实际中发电计划的编制。
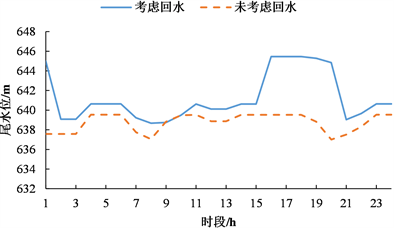 (a) 汛期
(a) 汛期
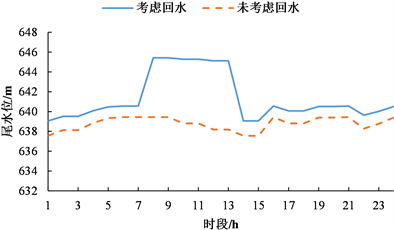 (b) 枯期
(b) 枯期
Figure 6. Comparison of tail water level with and without considering backwater
图6. 考虑回水与未考虑回水尾水位对比
5. 结语
本文针对水力联系紧密的“一库多级”水电站群,提出了考虑回水效应的精细化梯级水电站群短期优化调度MILP模型,并通过天生桥“一库两级”水电站群短期调度进行检验,得到结论如下:
1) 本文构建了“一库多级”水电站群短期调度MILP模型,重点处理了梯级水头联系:尾水位–泄量–库水位三维曲线。
2) 针对模型中的水位库容关系、尾水位–泄量–库水位关系、机组动力特性曲线以及机组振动区等非线性约束,采用分段线性化方法拟合,保留了原约束的特性,较好地贴近实际工况。
3) 以机组为基本调度单元,能有效满足振动区、机组开停机持续时间及最大开机次数约束等约束,保证了机组的稳定运行。
4) 采用Lingo软件求解红水河梯级实例,尽管模型中的约束和整数变量数目庞大,仍可在可接受的时间范围内求得全局最优解,为涉及回水问题的“一库多级”水电站群短期调度提供一种可靠的解决方法。
基金项目
国家重点研发计划(2016YFC0402208);水利部珠江河口动力学及伴生过程调控重点实验室开放研究基金([2018]KJ09);大连理工大学研究生教改基金项目(Jg2017013)。
文章引用
高 寒,申建建,苏承国,程春田,武新宇. 考虑回水效应的一库多级式水电站群短期优化调度模型
A Short-Term Optimal Scheduling Model of Cascaded Hydropower Stations with One Reservoir Considering the Effect of Backwater[J]. 水资源研究, 2019, 08(03): 248-259. https://doi.org/10.12677/JWRR.2019.83030
参考文献
- 1. CHENG, C., YAN, L., MIRCHI, A., et al. China’s booming hydropower: Systems modeling challenges and opportunities. Journal of Water Resources Planning and Management, 2016, 143(1): 02516002. https://doi.org/10.1061/(ASCE)WR.1943-5452.0000723
- 2. 申建建, 张楠男, 程春田, 等. 基于聚类分析和决策树的“一库多级”水电站日调度方法[J]. 中国电机工程学报, 2019, 39(3): 652-663+945. SHEN Jianjian, ZHANG Nannan, CHENG Chuntian, et al. Method for daily operation of hydropower stations with one reservoir based on cluster analysis and decision tree technique. Proceedings of the CSEE, 2019, 39(3): 652-663+945. (in Chinese)
- 3. WANG, J. Short-term generation scheduling model of Fujian hydro system. Energy Conversion and Management, 2009, 50(4): 1085-1094. https://doi.org/10.1016/j.enconman.2008.12.004
- 4. 申建建, 程春田, 李卫东, 等. 复杂时段耦合型约束水电站群短期变尺度优化调度方法[J]. 中国电机工程学报, 2014, 34(1): 87-95. SHEN Jianjian, CHENG Chuntian, LI Weidong, et al. A mutative-scale optimization method for short-term operation of hydropower plants with complex temporal coupling constraints. Proceedings of the CSEE, 2014, 34(1): 87-95. (in Chinese)
- 5. 李义, 李承军, 周建中. POA-DPSA混合算法在短期优化调度中的应用[J]. 水电能源科学, 2004, 22(1): 37-39. LI Yi, LI Chengjun and ZHOU Jianzhong. POA-DPSA algorithm for short-term hydro scheduling of cascaded hydroelectric stations. Water Resources and Power, 2004, 22(1): 37-39. (in Chinese)
- 6. JI, C., YU, H., WU, J., et al. Research on cascade reservoirs’ short-term optimal operation under the effect of reverse regulation. Water, 2018, 10(6): 808. https://doi.org/10.3390/w10060808
- 7. 苏承国, 王沛霖, 武新宇, 等. 考虑机组组合的梯级水电站短期调峰MILP模型[J]. 电网技术, 2018, 42(6): 1883-1891. SU Chengguo, WANG Peilin, WU Xinyu, et al. A compact MILP model for short-term peak shaving of cascaded hydropower plants considering unit commitment. Power System Technology, 2018, 42(6): 1883-1891. (in Chinese)
- 8. 徐鼎甲. 进行日调节时水电站下游水位的计算[J]. 水利水电技术, 1995(4): 2-4. XU Dingjia. Calculation of downstream water level of hydropower station during daily regulation. Water Resources and Hydropower Engineering, 1995(4): 2-4. (in Chinese)
- 9. LIU, B., CHENG, C., WANG, S., et al. Parallel chance-constrained dynamic programming for cascade hydropower system operation. Energy, 2018, 165: 752-767. https://doi.org/10.1016/j.energy.2018.09.140
- 10. 纪昌明, 马皓宇, 李传刚, 等. 基于可行域搜索映射的并行动态规划[J]. 水利学报, 2018, 49(6): 649-661. JI Changming, MA Haoyu, LI Chuangang, et al. Research on parallel dynamic programming based on feasible region search mapping. Journal of Hydraulic Engineering, 2018, 49(6): 649-661. (in Chinese)
- 11. 梅亚东. 梯级水库优化调度的有后效性动态规划模型及应用[J]. 水科学进展, 2000, 11(2): 194-198. MEI Yadong. Dynamic programming model without markovin property of cascade reservoirs operation and its application. Advances in Water Science, 2000, 11(2): 194-198. (in Chinese)
- 12. CATALAO, J. P. S., MARIANO, S. J. P. S., MENDES, V. M. F., et al. Scheduling of head-sensitive cascaded hydro systems: A nonlinear approach. IEEE Transactions on Power Systems, 2009, 24(1): 337-346. https://doi.org/10.1109/TPWRS.2008.2005708
- 13. BORGHETTI, A., et al. An MILP approach for short-term hydro scheduling and unit commitment with head-dependent reservoir. IEEE Transactions on Power Systems, 2008, 23(3): 1115-1124. https://doi.org/10.1109/TPWRS.2008.926704
- 14. CHENG, C., WANG, J. and WU, X. Hydro unit commitment with a head-sensitive reservoir and multiple vibration zones using MILP. IEEE Transactions on Power Systems, 2016, 31: 4842-4852. https://doi.org/10.1109/TPWRS.2016.2522469
- 15. GE, X. L., ZHANG, L. Z., SHU, J., et al. Short-term hydropower optimal scheduling considering the optimization of water time delay. Electric Power Systems Research, 2014, 110: 188-197. https://doi.org/10.1016/j.epsr.2014.01.015
