Statistics and Application
Vol.06 No.03(2017), Article ID:21699,13
pages
10.12677/SA.2017.63037
The Study of Seismic Reinsurance Pricing Question Based on POT Model
Qianru Meng1, Qin Shang2, Zhe Wang1
1School of Mathematical Sciences, Dalian University of Technology, Dalian Liaoning
2Faculty of Management and Economics, Dalian University of Technology, Dalian Liaoning

Received: Jul. 22nd, 2017; accepted: Aug. 11th, 2017; published: Aug. 15th, 2017

ABSTRACT
China is one of the countries with serious natural disasters in the world. But as an effective means to manage catastrophe risk, reinsurance develops immaturely in our country. In this paper, we take earthquake catastrophe for example. Basing on the direct economic loss data of the earthquake which exceed the M4.5 class from 1996 to 2015, we use POT model and the distribution of GPD to calculate earthquake catastrophe risk and give the VAR under different levels of confidence. In the end, by using the definition and properties of compound Poisson distribution, we put forward a method to calculate the net premium under different deductible undertaken by the reinsurance company. The paper provides theory reference and data support for the study of catastrophe reinsurance pricing question in our country.
Keywords:POT Model, Threshold, Compound Poisson Distribution, Reinsurance
基于POT模型的地震再保险定价研究
孟芊汝1,尚勤2,王喆1
1大连理工大学,数学与科学学院,辽宁 大连
2大连理工大学,管理与经济学部,辽宁 大连
收稿日期:2017年7月22日;录用日期:2017年8月11日;发布日期:2017年8月15日

摘 要
中国是世界上自然灾害最为严重的国家之一,而再保险作为巨灾风险管理的有效手段,在我国的发展极不成熟。本文以地震巨灾为例,基于中国大陆地区1996年至2015年4.5级以上地震造成的直接经济损失数据,运用POT模型和广义帕累托分布(Generalized Pareto Distribution, GDP)对地震巨灾风险进行测算,并给出不同的置信度水平下VaR。最后,利用复合泊松分布的定义和性质给出再保险公司在不同免赔额下净保费的计算方法。为我国巨灾再保险定价研究提供了理论参考和数据支持。
关键词 :POT模型,阈值,复合泊松分布,再保险

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
中国是世界上自然灾害最严重的几个国家之一,灾害种类多,发生频率高,分布地域广,造成损失大。如何从国家的高度对一国巨灾风险进行管理,是一个十分迫切的重大课题。从世界发达国家巨灾保险体制中,我们看到再保险在巨灾风险管理等方面的重要性,但同时也看到目前我国的再保险市场无论是在理论还是实践方面都尚不成熟 [1] 。
2016年“十三五”规划明确指出:“中国要加快建立巨灾保险制度,建立政府推动、市场运作、风险共担的多层次巨灾保险体系。”而在这之中,再保险市场的建立和完善无疑有着举足轻重的地位。
巨灾风险评估是巨灾再保险定价的首要内容,直接关系到巨灾再保险定价的准确性。而巨灾风险具有尖峰厚尾的特征,使用一般的风险度量模型,计算结果不可避免会存在一定偏差。极值理论中POT模型是目前最适宜刻画这类风险特征的方法之一。Hosking、Wallis (1987) [2] 对基于极值理论的广义帕累托分布的参数拟合方法进行了深入分析推动了POT模型的发展;Lai、Wu (2008) [3] 以台湾1971~2005年台风造成的水稻损失数据为例,使用POT模型对其进行拟合与传统的厚尾拟合分布进行对比,得到GPD对于厚尾损失拟合效果更好的结论。
有关再保险定价,很多学者已做出了杰出工作。Chi、Tan (2010) [4] 运用VaR、CVaR将原保险人的整体风险暴露最小化,研究了凸性分出损失函数下的最优停止损失再保险,奠定了尾部风险度量方法在再保险研究中的地位;Alejandro Balbás、Beatriz Balbás、Antonio Heras (2009) [5] 对不同尾部风险度量方法下最优再保险策略的稳定性进行了分析;Alba [6] 等人运用GPD对墨西哥的地震损失数据进行拟合,并计算了再保险合同下关于保险回归的问题;赵智红、李兴绪(2010) [7] 模拟出巨额损失数据,在POT模型下利用GPD对其进行拟合并进一步计算了超额再保险的净保费问题。
本文在前人研究的基础上,以我国地震直接经济损失数据为例,在POT模型下选取合适的阈值,运用GPD对其风险损失分布进行拟合,测算地震巨灾风险VaR。在此基础上,选取免赔的再保险方式,根据免赔额与阈值的大小关系不同,分三种情况计算再保险每份保单的年度净保费。由于现有对于再保险净保费的计算大多过于繁琐,故本文借鉴保险精算学中损失发生次数服从泊松分布进而赔偿总额服从复合泊松分布的性质对其进行简化。一定程度上为我国再保险市场的发展提供理论基础。
2. 基于GDP分布的POT模型
设 是独立同分布的随机变量,服从未知分布记作
是独立同分布的随机变量,服从未知分布记作 ,
,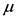 为某一充分大的阈值,设超过
为某一充分大的阈值,设超过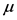 的样本个数为
的样本个数为 。若
。若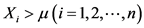 ,称
,称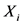 为超阈值,称
为超阈值,称 为超出量。称随机变量
为超出量。称随机变量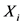 的超出量分布为条件超额分布函数。
的超出量分布为条件超额分布函数。

Pickands证明,当阈值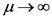 时,超额分布可以用GDP来近似 [8] :
时,超额分布可以用GDP来近似 [8] :

当 时,
时,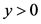 ;当
;当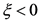 时,
时, 。其中
。其中 和
和 分别称为尺度参数和形状参数。
分别称为尺度参数和形状参数。 的不同取值决定了分布尾部的厚度,
的不同取值决定了分布尾部的厚度,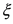 越大尾部越厚,
越大尾部越厚, 越小尾部越薄。
越小尾部越薄。
由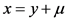 可得
可得

在确定了阈值后,对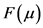 估计可采用历史模拟,即用
估计可采用历史模拟,即用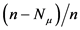 来近似表示
来近似表示 [9] ,进而总体分布函数
[9] ,进而总体分布函数

满足POT模型的分布一般呈现厚尾性,使用POT模型进行拟合,就不需要对整体分布进行假设。由于不受整体分布影响,残缺数据对POT模型的影响也较小,以此来拟合厚尾性强的中国地震灾害损失分布的效果较好。
3. 地震巨灾损失风险评估
3.1. 数据的获取与处理
本文通过对《中国地震年鉴》进行整理得到了我国大陆地区1996年至2015年来历次震级在4.5级以上地震(>=4.5级为破坏性地震)造成的直接经济损失,以其作为样本利用公式
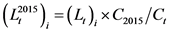
对损失数据进行物价调整。其中, 是在以2015年的物价水平为基期调整后的第
是在以2015年的物价水平为基期调整后的第 年第
年第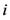 次地震的直接经济损失值;
次地震的直接经济损失值;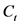 为第
为第 年的居民消费价格指数。
年的居民消费价格指数。
为避免出现明显的极端值情况,故采用取自然对数的方法进一步对数据进行处理减小数量级的差别以提高拟合精度 [10] 。
对对数化处理后的214个数据做直方图(图1)。
由对数化后的直方图中(图1)可以看出,损失数据呈现出明显的尖峰厚尾的性质。
3.2. 数据厚尾性检验
通常将分布函数的尾部比指数分布的尾部更厚的分布定义为厚尾分布。

Figure 1. The histogram of the logarithmic direct economic loss of each earthquake
图1. 经过对数处理的历次地震直接经济损失值直方图
从指数分布Q-Q图(图2)可以看出,上端向下倾斜,下端向上翘起,损失数据与指数分布之间存在着一个凹面的偏离,这说明数据存在厚尾的性质。从概率密度函数图中(图3)可以看到损失值顶部比正态分布更尖,尾部比正态分布更厚,呈现出明显的尖峰厚尾性质,且左偏。
同时可以利用峰度法来确定数据的厚尾性。峰度是用来度量数据在中心的聚集程度。在金融中,若某分布与正态分布有相同的方差,但是峰度系数大于3,则呈现“尖峰厚尾”形态,峰度更高,两段的尾部更厚,也就是极值更多的意思。对经过对数化的损失值求峰度可得

即可以认为该数据具有厚尾的性质。
3.3. 阈值的选取
GPD参数估计是否准确取决于阈值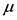 选取的适当与否。本文综合运用以下两种方法对阈值进行选取。
选取的适当与否。本文综合运用以下两种方法对阈值进行选取。
3.3.1. Hill图法
对于独立同分布的次序统计量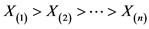 ,尾部指数的Hill统计量
,尾部指数的Hill统计量
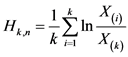
横轴为 ,纵轴为
,纵轴为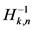 ,坐标为
,坐标为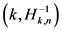 ,选取图中尾部指数稳定区域的起始点的横坐标对应的数值
,选取图中尾部指数稳定区域的起始点的横坐标对应的数值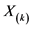 作为阈值
作为阈值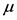 [11] 。
[11] 。
从Hill图(图4)中可以看出图像左边波动较大,右边比较平缓,图中出现的第一个比较平稳的部分对应的门限值为(10.90,11.60),相应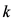 值为(28,47)。
值为(28,47)。

Figure 2. Q-Q plot for exponential distribution
图2. 指数分布Q-Q图

Figure 3. Density default
图3. 概率密度函数图
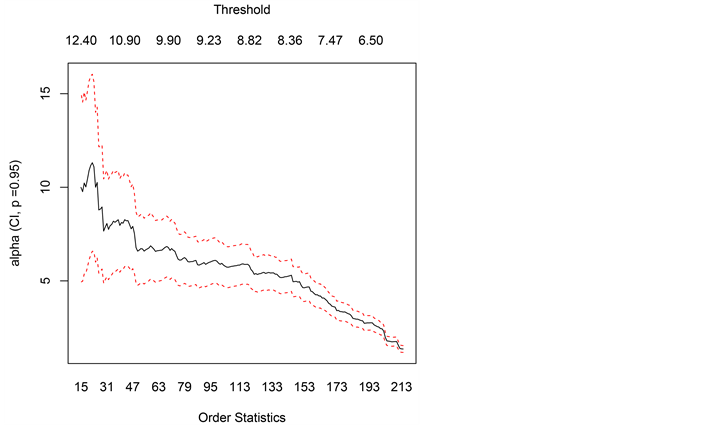
Figure 4. Hill plot
图4. Hill图
3.3.2. 超额均值函数图法
超额均值函数(Mean Excess Function, MEF)的定义为:
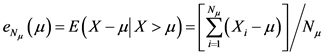
式中,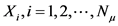 表示超过阈值的样本观测量。MEF图是点
表示超过阈值的样本观测量。MEF图是点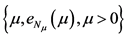 的集合。对于GPD,平均超出量函数是关于阈值
的集合。对于GPD,平均超出量函数是关于阈值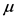 的线性函数,即
的线性函数,即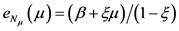 ,故如果在某个观测之后函数曲
,故如果在某个观测之后函数曲
线趋于线性且斜率为正,那么可以确定阈值 为该观测值。
为该观测值。
从图5可以看出,阈值约在区间在(11,12)的一个范围内图形是近似线性的,选取11.6为阈值,此时有28个数据超过了阈值。
综合上述两种方法,可以认为阈值选取为10.8是合理的。
3.4. 广义帕累托模型的建立
本文采用极大似然函数法对GPD参数进行估计,对数似然函数:

对函数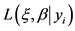 求偏导,使得函数值最大的
求偏导,使得函数值最大的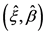 为最佳估计量。
为最佳估计量。
对选定的阈值 进行模型拟合,参数估计见表1。
进行模型拟合,参数估计见表1。
利用估计结果,我们可以进一步得到拟合分布的诊断图。
通过以上四个分布拟合诊断图(图6)看出,各数据点基本上分布在其参考线两侧。说明对我国1996~2015年间的次地震损失对数数据运用POT模型及广义帕累托分布拟合是合理的。对于广义帕累托
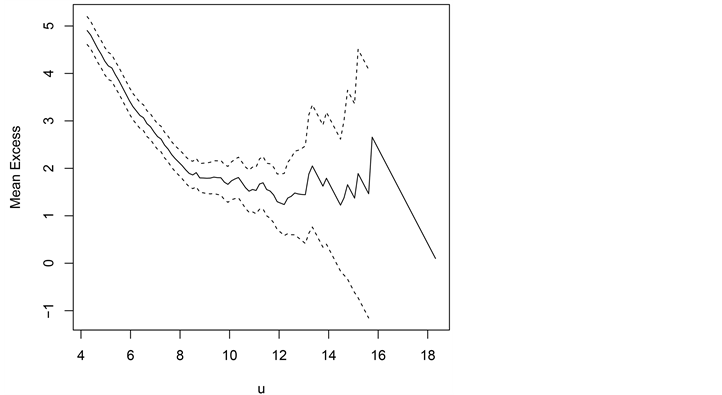
Figure 5. Mean excess function graph
图5. 超额均值函数图
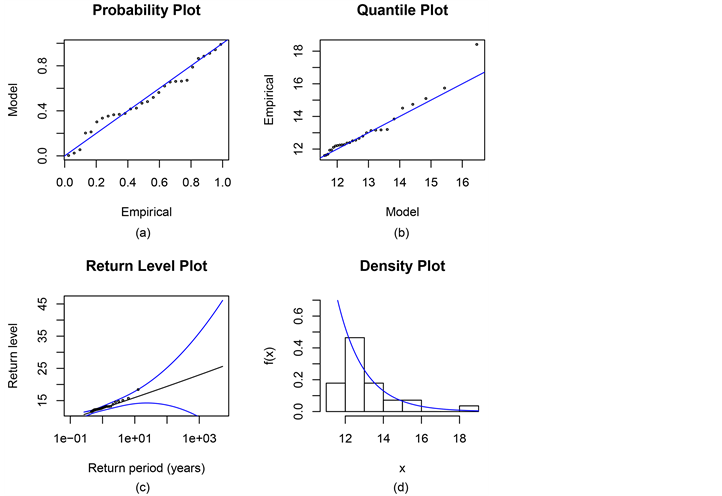
Figure 6. Generalized Pareto distribution fitting diagnostic map. (a) P-P graph (b) Q-Q graph (c) reproducing horizontal graph (d) histogram and density function estimation graph
图6. 广义Pareto分布拟合诊断图。(a) P-P图 (b) Q-Q图 (c) 重现水平图 (d) 直方图与密度函数估计图
Table 1. Generalized Pareto distribution parameter estimation table
表1. POT模型参数估计表
分布,还可以通过截断分布拟合、尾分布拟合、残差分布以及残差拟合来进一步的比较和检验。
从截断分布拟合图(图7)可以看出用广义帕累托分布对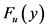 拟合较好,特别是对那些本文重点研究的巨额损失数据。从尾分布拟合图(图8)可以看出广义帕累托分布对损失数据的经验尾部函数也有很好的拟合。
拟合较好,特别是对那些本文重点研究的巨额损失数据。从尾分布拟合图(图8)可以看出广义帕累托分布对损失数据的经验尾部函数也有很好的拟合。
残差分布图(图9)可以看出残差主要分布在(0,2)内。残差拟合检验图(图10)可得出残差可以近似看作服从指数分布。因此,使用基于广义分布模型来拟合地震损失数据是合适的。
3.5. VAR的测度
风险价值VAR是指在一定时间和一定置信度内的潜在最大损失,一般可以定义为
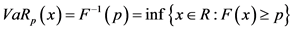 ,
, 
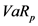 为损失分布的极大值,
为损失分布的极大值,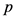 为置信水平,
为置信水平,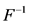 为分位函数,是损失分布
为分位函数,是损失分布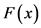 的逆函数。从统计学的角度讲,VAR可理解为给定分布下分位数的点估计值。
的逆函数。从统计学的角度讲,VAR可理解为给定分布下分位数的点估计值。
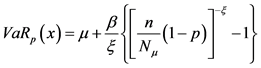
计算出不同的置信度水平下VAR不同的值,得到具体结果如表2所示。
上表说明在运用POT模型对地震巨灾损失分布进行拟合的情况下,正常状况下有85%的可能性认为发生一次地震的直接经济损失不超过8.972552亿元,有90%的可能性其损失值小于16.041203亿元,有95%的概率认为发生一次地震带来的直接经济损失最大为43.597309亿元,而发生一次地震造成的最大直接经济损失达到459.039335亿元的可能性为99%,一次地震带来的直接经济损失不超过1283.335682亿元的概率将高达99.5%。
4. 地震巨灾再保险定价
设一年内损失发生次数 服从参数为
服从参数为 的泊松分布,每次损失额
的泊松分布,每次损失额 ,
, ,独立同分布且分布与
,独立同分布且分布与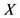 分布相同为
分布相同为 (非退化)。若再保险合同约定理赔按照免赔方式进行。那么再保险人赔款总额为
(非退化)。若再保险合同约定理赔按照免赔方式进行。那么再保险人赔款总额为
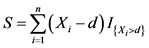
其中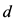 为免赔额。
为免赔额。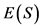 就是再保险年度净保费 [12] 。
就是再保险年度净保费 [12] 。
设赔款次数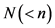 服从泊松分布,每次赔款额
服从泊松分布,每次赔款额 ,
,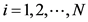 ,独立同分布且分布与
,独立同分布且分布与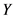 分布相同为
分布相同为 (非退化),赔款总额
(非退化),赔款总额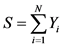 服从参数为
服从参数为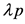 的复合泊松分布,其中
的复合泊松分布,其中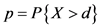 [13] 。故
[13] 。故
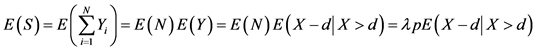
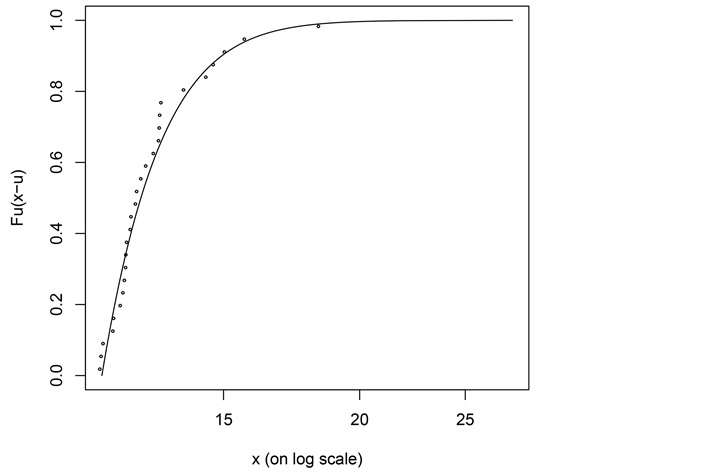
Figure 7. Fitted graph of truncated distribution
图7. 截断分布拟合图

Figure 8. Fitted graph of tail distribution
图8. 尾部分布拟合图
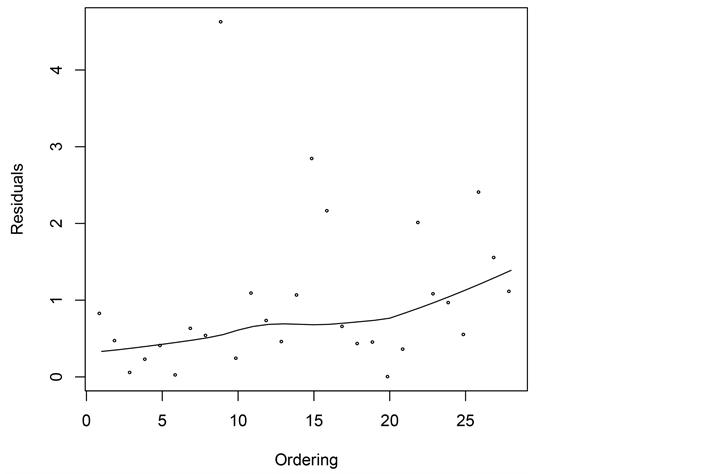
Figure 9. Residual plot
图9. 残差分布图
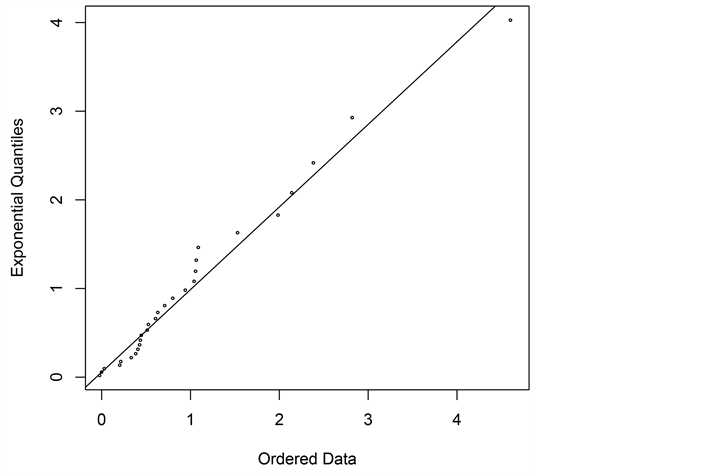
Figure 10. Fitted graph of residual
图10. 残差拟合图
Table 2. Premium scale calculation results
表2. 保费规模测算结果
若免赔额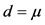 ,此时
,此时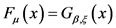
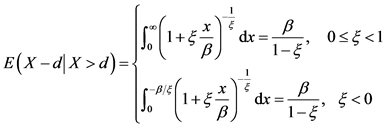
故再保险年度净保费为

当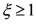 时,由于被积函数不收敛,即
时,由于被积函数不收敛,即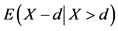 不存在,通常认为这种风险不可保。
不存在,通常认为这种风险不可保。
若免赔额 ,调整泊松参数为
,调整泊松参数为
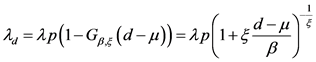
新的超出量分布函数为
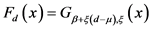
此时每次超出量的期望为
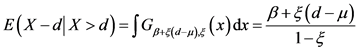
故再保险年度净保费为

若免赔额 ,由于GPD舍去了阈值之前的数据,此时需要寻找一个分布来描述阈值之前的损失部分,采用非参数方法,对整体进行核密度估计。记核密度估计为
,由于GPD舍去了阈值之前的数据,此时需要寻找一个分布来描述阈值之前的损失部分,采用非参数方法,对整体进行核密度估计。记核密度估计为
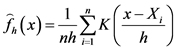
其中,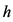 为窗宽,
为窗宽,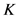 为核函数。
为核函数。
再保险年度净保费为

假设免赔额为阈值 ,再保险赔偿频率
,再保险赔偿频率 ,实际中可以令保险公司每张保单或保单组合赔偿次数的期望作为泊松分布的赔偿频率。
,实际中可以令保险公司每张保单或保单组合赔偿次数的期望作为泊松分布的赔偿频率。
此时

即再保险每单年度净保费为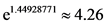 万元。
万元。
若再保险人只承担区间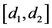 中的赔偿责任,则净保费为免赔额为
中的赔偿责任,则净保费为免赔额为 的净保费减去免赔额为
的净保费减去免赔额为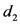 的净保费。
的净保费。
假设对地震巨灾风险损失的分担做以下简单分层:0~16.041203亿元之间的直接经济损失由国内保险机构承担,16.041203~43.597309亿元之间的直接经济损失由再保险市场承担;43.597309~459.039335亿元之间的直接经济损失可以通过设立巨灾债券等金融衍生品的形式将风险打包转移到资本市场;当损失超过了459.039335亿元时,政府最后买单。
则再保险每单年度净保费即为免赔额为11.98550的纯保费减去免赔额为12.98534的净保费。计算可得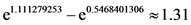 万元。
万元。
5. 结论
鉴于再保险市场的完善对于我国巨灾保险体制的构建具有重大意义,本文以我国大陆地区1996年至2015年来历次震级在4.5级以上地震造成的直接经济损失为例,构建POT模型综合运用不同方法选取合适的阈值并对GPD的参数进行拟合,利用拟合结果测度地震巨灾风险VAR,然后在此基础上,借鉴保险精算学中损失发生次数服从泊松分布赔偿总额服从复合泊松分布的性质,提出了一个以免赔方式进行的再保险合同,根据免赔额与阈值大小不同分为三类,计算出再保险人所要承担的每单保险年度净保费。研究结论为我国巨灾再保险定价提供了一定的理论参考和数据支持,有助于推动我国巨灾保险体系的构建。
基金项目
辽宁省社会科学规划基金项目(L16BGL012);辽宁省教育厅科学研究项目(L2014024)。
文章引用
孟芊汝,尚勤,王喆. 基于POT模型的地震再保险定价研究
The Study of Seismic Reinsurance Pricing Question Based on POT Model[J]. 统计学与应用, 2017, 06(03): 320-332. http://dx.doi.org/10.12677/SA.2017.63037
参考文献 (References)
- 1. 孙祁祥, 郑伟, 等. 中国巨灾风险管理:再保险角色[J]. 财贸经济, 2004(9): 3-10.
- 2. Hosking, J.R. and Wallis, J.R. (1987) Paremeter and Quantile Estimation for Generalize Pareto Distribution. Techno-Metrics, 29, 339-349. https://doi.org/10.1080/00401706.1987.10488243
- 3. Lai, L.-H. and Wu, P.-H. (2008) Estimating the Threshold Value and Loss Distribution: Rice Damaged by Typhoons in Taiwan. African Journal of Agricultural Research, 3, 818-824.
- 4. Chi, Y. and Tan, K.S. (2010) Optimal Reinsurance under VaR and CVaR Risk Measures: A Simple Approach. ASTIN Bulletin, 41, 487-509.
- 5. Balbás, A., Balbás, B. and Heras, A. (2009) Optimal Reinsurance with General Risk Measures. Insurance: Mathematics and Economics, 44, 374-384.
- 6. De Alba, E., Zúñiga, J. and Ramírez Corzo, M.A. (2008) Measurement and Transfer of Catastrophic Risks: A Simulation Analysis. ASTIN Bulletin, 40, 547-568.
- 7. 赵智红, 李兴绪. 非寿险中巨额损失数据的拟合与精算[J]. 数理统计与管理, 2010, 29(3): 336-347.
- 8. Balkema, A. and Haan, D.L. (1974) Residual Life Time at Great Age. Ann Probab, 9, 792-804.
- 9. 桂文林. POT模型中GPD厚尾性及金融风险测度[J]. 数量经济技术经济研究, 2010, 10(1): 107-118.
- 10. 郝军章, 崔玉杰. 基于模型的巨灾风险度量与保险模式研究——以地震风险为例[J]. 数理统计与管理, 2015, 35(1): 132-141.
- 11. Embrechts, P. and Mikosch, T. (1997) Modelling Extremal Events for Insurance and Finance. Springer-Verlag, London, 102-130. https://doi.org/10.1007/978-3-642-33483-2
- 12. 肖海清, 孟生旺. 极值理论及其在巨灾再保险定价中的应用[J]. 数理统计与管理, 2013, 32(2): 240-246.
- 13. 任婧, 张节松. 基于POT模型的巨灾损失分布拟合及风险度量[J]. 科技与管理, 2015, 17(1): 75-80.
