Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18349,8
pages
10.12677/AAM.2016.53045
The Behavior of a Class of Functions Containing Parameter
Qi Wang1,2, Weiling You2*, Chunpeng Mo2
1School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong
2College of Science, College of Vocational and Technical Education, Guangxi University of Science and Technology, Liuzhou Guangxi

Received: Jul. 26th, 2016; accepted: Aug. 15th, 2016; published: Aug. 18th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we investigate a class of functions containing parameter and reveal the nature of the function with different parameters. We also use matlab to simulate the results, which verify the correctness of the conclusions.
Keywords:Stable Point, Zero Point, Eventually Monotone Increasing (Decreasing)

一类含参变量函数的性态
王琦1,2,尤卫玲2*,莫春鹏2
1广州大学,数学与信息科学学院,广东 广州
2广西科技大学,理学院、职业技术教育学院,广西 柳州

收稿日期:2016年7月26日;录用日期:2016年8月15日;发布日期:2016年8月18日

摘 要
本文考察一类含参变量的函数,揭示函数在参数不同取值下的性态,并利用matlab进行了仿真,结果验证结论的正确性。
关键词 :稳定点,零点,最终单调递增(减)

1. 引言
从现有的文献来看,对含参变量函数性态的研究甚少,而多数都是讨论含参变量函数的积分、Riemann边值问题或Hilbert边值问题 [1] - [3] ,梅宏则在文献 [4] 中给出了一类含参变量积分的常差分方程计算方法。
本文对一类特殊的带参变量函数的进行分析,揭示该类函数在参数不同取值下的性态。
本文考察如下函数:
 ,
,
其中参数 。
。
2. 主要结果
首先,函数 对
对 求导数
求导数
 ,
,
令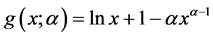 ,则有
,则有
 (1)
(1)
同样,函数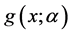 对
对 求导数
求导数
 ,
,
再令 ,则有
,则有
 (2)
(2)
当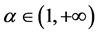 时,记
时,记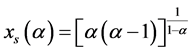 ,显然
,显然 ,因而
,因而 是函数
是函数 的稳定点。
的稳定点。
引理1 对于函数 和
和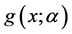 ,下述成立:
,下述成立:
(i) 当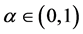 时,对于任意
时,对于任意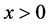 ,有
,有 ,从而
,从而 关于
关于 在
在 上严格单调递增。
上严格单调递增。
(ii) 当 时,对于任意
时,对于任意 ,有
,有 ,从而
,从而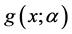 关于
关于 在
在 上严格单调递增。
上严格单调递增。
(iii) 当 时,有表1成立。
时,有表1成立。
Table 1. The monotonicity of the function at the case
表1. 函数 在
在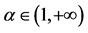 下的单调性
下的单调性
且 。
。
证明 (i) 当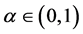 时,对于任意
时,对于任意 ,有
,有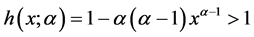 ,由(2)知,
,由(2)知, 关于
关于 在
在 上严格单调递增。
上严格单调递增。
(ii) 当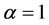 时,对于任意
时,对于任意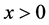 ,有
,有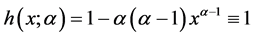 ,由(2)知,
,由(2)知, 关于
关于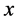 在
在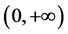 上严格单调递增。
上严格单调递增。
(iii) 当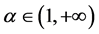 时,注意到对任意
时,注意到对任意 ,有
,有 ,所以
,所以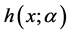 在
在 上关于
上关于 严格单调递减。而
严格单调递减。而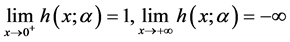 ,所以存在唯一的
,所以存在唯一的 使得
使得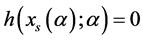 ,再结合(2)知表1成立。而
,再结合(2)知表1成立。而 显然成立。注意到
显然成立。注意到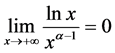 ,故
,故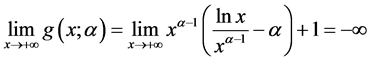 。因而
。因而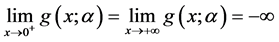 。
。
定理1 对于函数 和
和 ,下述成立:
,下述成立:
(i) 当 时,
时,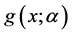 存在零点
存在零点 ,有表2成立。
,有表2成立。
且 。
。
(ii) 当 时,有表3成立。
时,有表3成立。
(iii) 存在 满足
满足 ,且
,且
(a) 当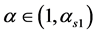 时,存在
时,存在 及
及 使得表4成立。
使得表4成立。
(b) 当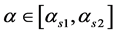 时,有表5成立。
时,有表5成立。
(c) 当 时,存在
时,存在 及
及 使得表6成立。
使得表6成立。
证明 (i) 当 时,注意到
时,注意到 ,
, ,再结合(1)、(2)及引理1 (i)可知,存在
,再结合(1)、(2)及引理1 (i)可知,存在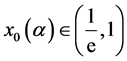 使得
使得 ,从而表2成立。显然
,从而表2成立。显然 ,
, 。
。
(ii) 当 时,注意到
时,注意到 ,
, 及
及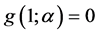 ,再结合(1)、(2)及引理1 (ii)可知表3成立。
,再结合(1)、(2)及引理1 (ii)可知表3成立。
(iii) 当 时,记
时,记 ,由引理1 (iii)知
,由引理1 (iii)知 。由
。由 ,解得
,解得 ,而
,而
Table 2. The monotonicity of the function at the case
表2. 函数 在
在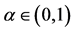 下的单调性
下的单调性
Table 3. The monotonicity of the function at the case
表3. 函数 在
在 下的单调性
下的单调性
Table 4. The monotonicity of the function at the case
表4. 函数 在
在 下的单调性
下的单调性
Table 5. The monotonicity of the function at the case
表5. 函数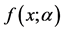 在
在 下的单调性
下的单调性
Table 6. The monotonicity of the function at the case
表6. 函数 在
在 下的单调性
下的单调性
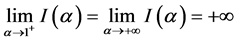 ,从而有表7成立。
,从而有表7成立。
令 ,可得
,可得 满足
满足 ,且有表8成立。
,且有表8成立。
(a) 当 时,由表8可知
时,由表8可知 ,再结合引理1 (iii)及(1)知,存在
,再结合引理1 (iii)及(1)知,存在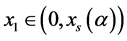 及
及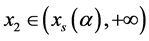 使得表4成立。
使得表4成立。
(b) 当 时,由表8可知
时,由表8可知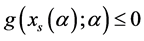 ,再结合引理1 (iii)及(1)知表5成立。
,再结合引理1 (iii)及(1)知表5成立。
Table 7. The monotonicity of the function I(α)
表7. 函数I(α)的单调性
Table 8. The value of the function
表8. 函数 的取值
的取值
(c) 当 时,由表8可知
时,由表8可知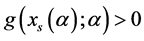 ,再结合引理1(iii)及(1)知,存在
,再结合引理1(iii)及(1)知,存在 及
及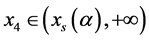 使得表6成立。
使得表6成立。
定理2 对于函数 ,下述成立:
,下述成立:
(i) 当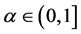 时,
时,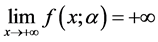 。
。
(ii) 当 时,
时, 。
。
证明 (i) 当 时,由定理1知,
时,由定理1知, 是关于变量
是关于变量 最终单调递增的,所以不妨设
最终单调递增的,所以不妨设 。显然
。显然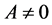 ,下证
,下证 。反证,假设
。反证,假设 ,则
,则
 ,
,
与假设矛盾,因而 。
。
(ii) 当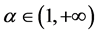 时,由定理1知,
时,由定理1知,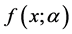 是关于变量
是关于变量 最终单调递减的,注意到对任意
最终单调递减的,注意到对任意 有
有 ,所以不妨设
,所以不妨设 。显然
。显然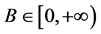 ,下证
,下证 。
。
 ,
,
即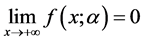 。
。
定理3 对于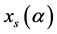 有
有

且 ,
,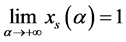 。
。
证明 当 时,方便起见,记
时,方便起见,记 ,
, 。则
。则
 。
。
将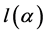 对
对 分别求一阶导数和二阶导数
分别求一阶导数和二阶导数
 ,
,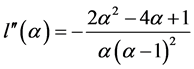 ,
,
令 ,得
,得 。注意到
。注意到 ,所以有表9成立。
,所以有表9成立。
即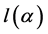 在
在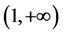 上严格单调递减。而
上严格单调递减。而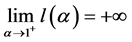 ,
, ,所以存在唯一一点
,所以存在唯一一点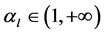 ,使得
,使得 ,亦即
,亦即 。而
。而 ,
, ,
, ,从而有表10成立。
,从而有表10成立。
因此存在唯一一点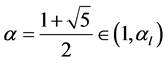 使得
使得 ,且当
,且当 时,
时, ;当
;当 时,
时,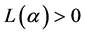 。由
。由 ,
, ,知
,知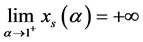 ,
,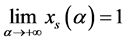 。
。
Table 9. The monotonicity of the function
表9. 函数 的单调性
的单调性
Table 10. The monotonicity of the function
表10. 函数 的单调性
的单调性
3. 数值仿真
这一部分我们用matlab描绘在参数 不同取值下函数
不同取值下函数 的图像。
的图像。
当 时,函数
时,函数 在参数
在参数 不同取值下的图像如图1所示。
不同取值下的图像如图1所示。
当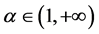 时,函数
时,函数 在参数
在参数 不同取值下的图像如图2所示。
不同取值下的图像如图2所示。
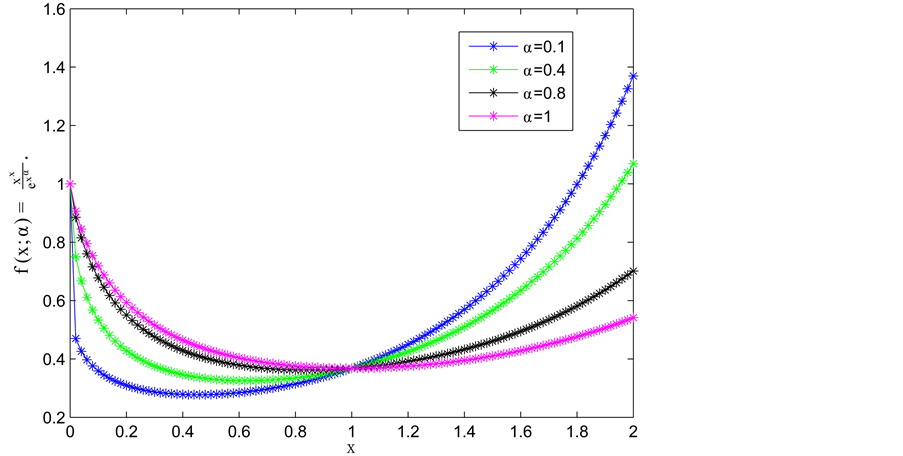
Figure 1. The figure of 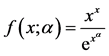 with the parameter
with the parameter 
图1.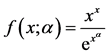 在参数
在参数 下的图像
下的图像

Figure 2. The figure of  with the parameter
with the parameter 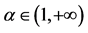
图2.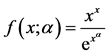 在参数
在参数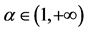 下的图像
下的图像
4. 小结
本文引入函数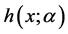 和
和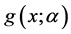 ,通过考察其性质(引理1)进而考察函数
,通过考察其性质(引理1)进而考察函数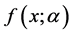 的性质(定理1、定理2)。接着考察了函数
的性质(定理1、定理2)。接着考察了函数 的稳定点
的稳定点 (定理3),为分类参数
(定理3),为分类参数 的区间进而准确描绘函数
的区间进而准确描绘函数 的图像做了准备。
的图像做了准备。
基金项目
国家自然科学基金资助项目(11461002);广西高校科学技术研究资助项目(LX2014194);广西高等教育本科教学改革工程资助项目(2015JGB296);2015年本科高校优势特色专业项目——测控技术与物联网工程;2014年自治区级辅导员精品项目——基于“易班”网络平台,加强班级电子档案建设,促进思想政治教育实效性;2016年度广西科技大学教育教学改革研究立项项目——职业化视角下思想政治教育融入大学生就业指导的模式研究,地方工科院校《数学分析》课程的教学研究与探索。
文章引用
王琦,尤卫玲,莫春鹏. 一类含参变量函数的性态
The Behavior of a Class of Functions Containing Parameter[J]. 应用数学进展, 2016, 05(03): 367-374. http://dx.doi.org/10.12677/AAM.2016.53045
参考文献 (References)
