Advances in Applied Mathematics
Vol.07 No.04(2018), Article ID:24567,4
pages
10.12677/AAM.2018.74041
Incidence Coloring of Graphs G with
Zhenzhen Li1, Xiaoping Liu2
1College of Mathematics and System Sciences, Xinjiang University, Urumqi Xinjiang
2College of Mathematics and System Sciences, Xinjiang Institute of Engineering, Urumqi Xinjiang

Received: Apr. 7th, 2018; accepted: Apr. 19th, 2018; published: Apr. 26th, 2018

ABSTRACT
An incidence in a graph G is a pair (v,e), where v is a vertex of G and e is an edge of G incidence to v. Two incidence (v,e) and (u,f) are a djacent if at least one of the following holds: u = v, or e = f or . An incidence coloring of G is a coloring of its incidence assigning distinct colors to adjacent incidences. The incidence chromatic number of G, denoted by , is the smallest number of colors used in a incidence coloring of G. Recently, Gregor, luzar, and Sotak showed that for a graph G with maximum degree at most 4. The aim of the present paper is to present a short proof of this result.
Keywords:Incidence Coloring, Incidence Chromatic Number
最大度为4的图的关联着色数
李珍珍1,刘晓平2
1新疆大学数学与系统科学学院,新疆 乌鲁木齐
2新疆工程学院,新疆 乌鲁木齐
收稿日期:2018年4月7日;录用日期:2018年4月19日;发布日期:2018年4月26日

摘 要
图中的关联是由图G中的顶点v和图G中与v关联的边e所构成的有序对(v,e),两个关联对(v,e)和(u,f)相邻当且仅当u = v或e = f或 成立。图的关联着色是指对图中G的关联有序对进行着色,使得相邻关联对着不同的颜色。图G的关联色数 ,是指图G的所有关联着色方式中使用的最小颜色的个数。近期,Gregor,luzar和Sotak证明对于 的图G, 。本文主要目标是对于这一结果给以短的证明。
关键词 :关联着色,关联着色数

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
图的关联着色的概念是在1993年由Brualdi和Massy [1] 引入的。图G的关联是指由图G中相关联的点v和边e构成的有序对(v,e)。我们称两个关联(v,e)和(u,f)相邻当且仅当,u = v或e = f或 成立。图G的关联着色是指对图G中相邻的关联给以不同的颜色。图G的所有关联着色方式中所用的最少颜色数称为图G的关联着色数,记为 。Brualdi和Massy [1] 提出猜想:对任意图G, 。这一猜想在1997年被Guiduli [2] 证明是错误的。但是外平面图、超立方体图等诸多图类使猜想成立。Maydanskiy [3] 证明了Brualdi-Massy猜想对3-正则图成立。
引理1.1:(Maydanskiy [3] )对任意3-正则图G, .
近期,Gregor, Luzar, Sotak [4] 证明了下述定理:
定理1.2:(Gregor, Luzar, Sotak [4] )若G是一个最大度为4的图,则 。
本篇文章主要目标是对这个定理1.2给予新的简短证明。
我们证明的主要思想是借助于Guiduli [2] 提出的关联着色数的一个等价形式。如果一个有向图D,它的连通分支都是有向星(边的方向由中心点指向外),我们称D为有向星森林。一个有向图D的有向星荫度 [5] ,记为 ,是指覆盖D的所有弧所用的有向星森林数的最小值。一个图G的伴随有向图,记为D(G),是把G的每条边用一对双向弧替代所得到的有向图。图G的一个关联对 可看作是D(G)的指向v的一个弧,这样图G的一个关联着色就转化为D(G)的弧着色,其每个色类都是一个有向星森林。因此,任何图G, 。
2. 定理1.2的证明
如果 ,由定理1.1,结论成立。以下对 的情形进行证明.
首先,用Gregor,Luzar,与Sotak [4] 所用方法,选取G的一个最大匹配M。则 是一个独立集。用A表示G中所有未被M覆盖的4度点的集合。为了描述方便,我们称 中点及M中边为红色点或红色边,A中点为黑色点。显然G中可能会有既不是黑色又不是红色的点。由Hall定理可证明存在匹配 覆盖点集A。我们称 中边为黑色边。令 ,并称 中边为蓝色边。如图1所示。
注意到 中任意两个元素不会与 中同一边的两个端点关联,由M与 选取可得 。由定理1.1,存在 的弧着色 使得其每个色类都是一个有向星森林。对于任意点x,我们用 表示 中与点x关联的弧所用的颜色集。
下面我们所采用的步骤有别于Gregor,Luzar,与Sotak [4] 的证明方法:修改 ,进而得到我们所希望的D(G)的弧着色。
步骤1. 对图G的黑色边 ,着D(G)中弧 颜色 , 。注意到,这里可能存在蓝色边 使得弧 满足 。如果这种情况发生,我们把蓝色弧b所着的颜色去掉。
经过步骤1,图D(G)中没有着色的弧由以下三类集合构成:所有红色弧构成的集合,由N(A)指向A的黑色弧所构成集合,步骤1中蓝色弧b所构成的集合。用 表示由D(G)中没有被着色的弧所导出的D(G)的子有向图,如图2所示。
以下证明 。由M是最大匹配,得 具有下列性质:
1) ,x所关联的弧为黑色或蓝色;
2) 任意两条蓝色弧的头部端点互不相同;
3) 如果红色边uv的两个端点都与非红色弧关联,则 且 (如图2中的 )。
由上述性质((1)~(3))知, 的任 意连通分支 同构于 ,C或 (如图2)。显然有 且 ,因此我们假定 既不同构于 ,也不同构于 。对 可以借助于步骤1对 的选择做适当调整,使得任意连通分支都不包含黑蓝边交错圈 , ,这类连通分支如图2中C。
如果经过步骤1所得到的 的连通分支C中包含黑蓝边交错圈 , 则对 中黑色弧 的对应颜色 重新选择(此时 至少有两种选着),通过改变 的选择消去圈 再次得到图 ,此时中若包含 ,重复此过程且不选择相同黑色弧做颜色替换,依次下去,考虑到性质(1)及点的度数限制,有限步可得到 ,使其连通分支都不包含黑蓝边交错圈 , 。
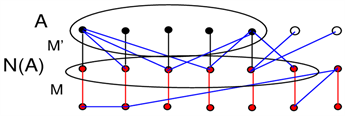
Figure 1. M, M', G' and their colors
图1. M,M',G'及它们的颜色
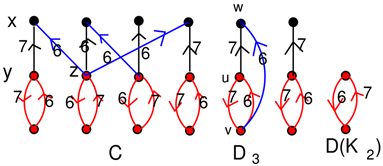
Figure 2. The subdigraph D' and its possible component or
图2. 子有向图D'及其可能的分支
步骤2. 对与图C同构的连通分支进行弧着色,首先把图中C蓝色弧用颜色6进行着色,且对图C中与蓝色弧具有相同尾部端点的红色弧和黑色弧用颜色6进行着色;其次把剩余的未被着色的黑色弧全部着7色并且把与黑色弧有公共尾部端点的红色弧着为颜色7;最后把所有未被着色的红色弧用颜色6进行弧着色(如图2),因中C不具有黑蓝边交错圈 , ,此着色方式可行。
通过步骤2所得的C中的每个色类均为有向星森林,所以 。
因此, 。
文章引用
李珍珍,刘晓平. 最大度为4的图的关联着色数
Incidence Coloring of Graphs G with Δ(G)≤4*[J]. 应用数学进展, 2018, 07(04): 334-337. https://doi.org/10.12677/AAM.2018.74041
参考文献
- 1. Brualdi, R.A. and Massy, J.J.Q. (1993) Incidence and Strong Edge Colorings of Graphs. Discrete Mathematics, 122, 51-58. https://doi.org/10.1016/0012-365X(93)90286-3
- 2. Guiduli, B. (1997) On Incidence Coloring and Star Arboricity of Graphs. Discrete Mathematics, 163, 275-278. https://doi.org/10.1016/0012-365X(95)00342-T
- 3. Maydanskiy, M. (2005) The Incidence Coloring Conjecture for Graphs of Maximum Degree 3. Discrete Mathematics, 292, 131-141. https://doi.org/10.1016/j.disc.2005.02.003
- 4. Gregor, P., Luzar, B. and Sotak, R. (2017) Note on Incidence Chromatic Number of Subquartic Graphs. Journal of Combinatorial Optimization, 34, 174-181. https://doi.org/10.1007/s10878-016-0072-2
- 5. Algor, I. and Alon, N. (1989) The Star Arboricity of Graphs. Discrete Mathematics, 75, 11-22. https://doi.org/10.1016/0012-365X(89)90073-3