Advances in Applied Mathematics
Vol.
07
No.
09
(
2018
), Article ID:
26805
,
7
pages
10.12677/AAM.2018.79135
Three Necessary Reforms in Linear Algebra for Engineering
—Introduction to Book “Applied Linear Algebra with MATLAB”
Huaichen Chen1, Wei Yang2
1School of Electronics Engineering, Xidian University, Xi’an Shaanxi
2School of Physics and Optoelectronic Engineering, Xidian University, Xi’an Shaanxi

Received: Aug. 23rd, 2018; accepted: Sep. 6th, 2018; published: Sep. 13th, 2018

ABSTRACT
Using reverse thinking method, dozens of engineering linear algebra problems were solved. We found that the biggest obstacle is the complexity of calculation, so computerization is the first key point. Showing innovative solutions using computer surpassing the old ones in engineering courses is the second point. The third is the deletion of useless mathematics theory. According to these principles, the textbook of “Applied Popular Linear Algebra with MATLAB” and its MOOC was launched.
Keywords:Linear Algebra, Determinant, Matrix Operation, Computerized Solution, MATLAB
工科线性代数必需的三项改革
—介绍《实用大众线性代数(MATLAB版)》教材 [1] 及其慕课
陈怀琛1,杨威2
1西安电子科技大学,电子工程学院,陕西 西安
2西安电子科技大学,物理与光电工程学院,陕西 西安

收稿日期:2018年8月23日;录用日期:2018年9月6日;发布日期:2018年9月13日

摘 要
用逆向思维的方法,从大量工程应用题解的实践中总结出:使用线性代数的第一个难点是“计算太复杂”,因此计算机化是改革的第一重点;第二个重点是必须能证明用线性代数解题是学科交叉的创新,比用旧方法好得多;第三个重点是要扬弃繁琐无用的数学理论,选择真正有用的内容,使大一学生能够接受。根据这三条原则,写成了《实用大众线性代数(MATLAB版)》教材,并制作成慕课(MOOC)播放,深受好评。
关键词 :线性代数,行列式,矩阵运算,计算机解题,MATLAB

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
线性代数成为我国非数学专业(下简称工科)基础课已经有三十多年了。但它与工科的课程仍然是两张皮,格格不入。表现在大学的四年中,几乎没有一门后续课程用到线性代数。一些大量用线性方程组建模的课程(如电路、力学等),学生仍在用中学代数解题。如果大学各课中不用,这怎么体现它的“基础课”地位?我觉得把线代植入工科的指导者们存在着一个认识问题:以为只要把原来数学系的内容照搬过来就行了,没认识到这是一个学科交叉(与工科结合),新旧替代(与计算机融合)的创造性的工作。为什么1950年前的两百多年,工科没有要这门课,而计算机出现后,就都要它做基础课了?他们看中了线性代数的哪一点?你满足了他们的需要吗?这是要深入思考的。
2. 线性代数能成为工科的数学工具吗?答案是:必须“现代化”
线性代数的经典理论早已相当成熟了,但工程系从来不学它,其主要原因是它的运算太费时,无法解决实际问题。没有线性代数,用中学代数大家都会解二元方程组,三元方程组就很烦了。学线代的目的本来是想学解题的新方法,但这些新方法并不简单,且其书写的格式还很麻烦,比初等代数要多花几倍的时间和纸张。比如一个三阶方阵求逆:
若 ,则
其中: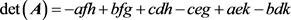 。
。
不难数出,式中包括了39个乘除和15个加减运算,无人肯笔算的!线代中的其他矩阵运算,求行列式、求相关性、求特征向量、……、无不如此,更何谈高阶和复数。所以两百年来它进不了工科教学计划的直接原因,就在于它的计算太繁琐,不是人干的活。
1950年代计算机的发明改变了这种局面。1970年代,线性代数软件包LINPACK开发成功,并诞生了MATLAB等矩阵软件工具,求一个几十阶方阵的逆只要几秒钟。工程界看到了它的价值,从那时起,世界各国都把线性代数引进了教学计划中,并成为必修的基础课。因为大学本科中许多课程都包含了线性代数方程组,工科希望能用新的方法来解。没想到这些线代老师带来的仍然是古典的代数方法,没有把最新的计算机解题技术带来,那当然使工科师生大失所望。
许多线代老师在序言中给学生吹嘘将来的科研中会遇到成千上万阶的方程组,要用到线代和计算机来解决。但不知为什么不在后续课中找一个三四阶的方程组来做实例呢?问题就在于他们都要刻意避开计算机。其实线性代数需要的“现代化”,恰好就可从这里起步。美国在1990年提出的改革线性代数的五条建议中,使用最新的计算技术就是其中之一。2009年我国高教司也立项支持以西电牵头的19所大学进行了“线性代数 + MATLAB”的成功教学试点,多数学校坚持至今。美国的改革已经普及了近30年,中国也宣传了10年,但不见普遍的行动,有那么难吗?
入MATLAB的门,用一两天就够了,然后在实践中提高。学生在大一学会MATLAB后,不仅节省了线性代数讲课和做题的时间,对其以后的学习和研究都起了很大的作用。为什么推广那么难?这一条不改,就意味着老师们自己不用线代,也没想让工科学生用。
3. 线性代数能成为工科各课的基础吗?答案是:能,但必须“实用化”
现代大规模的工程和经济问题几乎都需要用它来建模和求解,可称之为“实用化”。在学校内,我们在工科的大量后续课(力学、电路、信号处理、自动控制……等课程)中都存在着高阶线性方程组,但都在用笨办法求解,一旦用线性代数+MATLAB,就会出现飞跃。“实用化”比“现代化”难。因为这涉及工程和数学两者的结合,需要跨学科的创新。创新者必须同时懂得数学和相关的工程学科,随便举几门课加以说明:
例1. 空间解析几何题:给出空间三点的坐标如表1所示,求由通过此三点的平面的方程。
Table 1. Three Given Points on the plane
表1. 例1要求平面通过的空间三点坐标
解:平面方程的标准形式为c1x + c2y + c3z = 1,先求三个用方向余弦c1,c2,c3。将此三点的坐标分代入,可以得出三个联立方程,用矩阵表示此方程组:
用MATLAB程序语句求解,程序为:
A = [−2, 0, −5; 5, 1, −1; 0, −2, −1]; B = [1; 1; 1]; V = inv(A), c = V * B,在MATLAB中执行此语句,得:
c1 = 0.2143, c2 = −0.3571, c3 = −0.2857。
于是该平面的方程为0.2143x − 0.3571y − 0.2857z = 1。
例2. 电路题:根据电路图1,求出Ia,Ib,Ic。

Figure 1. A three loop resistance network
图1. 一个三回路电阻网络
列出此电路的方程组,写成矩阵模型如下:
在这里我们又看到了三元线性方程组求解,可化成矩阵运算。在实际工程中,此矩阵的阶数可能达到几十。如果是交流电路,其变量和系数都是复数。现在的电路课,不用线代,不能用矩阵机算。回路一多,就没法算,如果能用线代 + 计算机,那就帮了电路课的大忙了!
例3. 信号与系统题根据图2所示的信号流图,求出它的传输函数w4 = x4/u。
此信号流图的方程组和矩阵模型如下:
用MATLAB求解结果为: 。
谁也不敢用笔算解这个四阶矩阵方程。
这方法可以用于分析数字滤波器,以便根据其结构图求出全系统的传输函数。我们试算过一个数字滤波器,13阶的矩阵求逆,一秒钟就得到了解。
目前信号与系统课程中对这类问题的解法是把它分成多个小系统,两两合成,它等价于初等代数的消元法。也有人推导了很繁琐的图解方法(例如称为梅森公式的方法),效率极低又很易出错。线性代数的方法则是创新地建立全系统的联立方程组,再化成矩阵模型用MATLAB求解。理论严密,又快速精确。
例4. 自动控制题 系统传递函数的计算(图3)

Figure 2. A dual feedback signal flow graph
图2. 一个双反馈信号流图
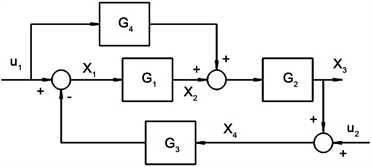
Figure 3. A control system structure diagram
图3. 一个控制系统结构图
输入U是2 × 1向量,输出X是5 × 1向量,Q是5 × 5方阵,求出的传递函数W是5 × 2矩阵。
一次MATLAB运行中竟然求出了十个传递函数。在传统的自动控制原理中,只能一个一个地求,每求一个都要对各环节做运算变换,极易出错。像本例这样快速的全局处理,是无法想象的。看到这样的例题,工程界就不能不承认线性代数的基础和创新的意义。但若不与计算机联系起来,手工来对这个五阶矩阵求逆几乎不可能,所以只用笔算的线性代数没有工程用途。
由这些例子可见,多元线性方程组,大一的课就开始有,用不到等到毕业以后。它涉及基本的线性物理过程的交叉叠合,都应该属于线性代数处理的范畴。作者写的《实用大众线性代数》教材中,举了多达46个各学科的应用实例来证明其实用性。目的是想弥补现有线性代数书的短板,使它具备工科味,使任课教师和学生有感性的体验。只有线性代数能帮助工科这样的大忙,才能得到工科尊重。够不够基础课的格,不能由线性代数老师自我吹嘘,要看实际效果。一个专业能找到几门这样的课程,这个专业就能心悦诚服地承认线性代数是其基础课;如果一点忙也帮不上,叫什么基础课呢?
4. 怎样处理线性代数中对工科无用的理论:做到“大众化”
经典线性代数在两百多年的发展中,积累了深厚的理论成果,但很多内容是偏重数学抽象,适用于数学系高年级,并没有现实的工程意义。现在要教的对象是工科一年级新生以及数以千万计的在职工程师,需要引导他们用线代来解决工程问题。那就必须去除无工程意义的内容,把最必需的理论教给学生。寻找的方法有两种:一是从顶向下,从现有的理论中删除无用的,这很难定标准;二是从底向上,把实际问题中用到的理论搜集整理,凡是没用到过的就予以排除。后一种方法完全从实际出发,是最能站住脚的,但必须有大量的较全面的应用实例作为基础。
作者为了写书 [2] [3] [4] 在近20年中曾做过大量用到线代的题,涉及机电专业十多门后续课。我们取了46例。大体情况是:1) 矩阵四则运算和求逆12例;2) 线性方程组求解22例(最高7阶,内超定5,欠定3,其余适定);3) 向量空间关系和运动变换8例;4) 线性变换和特征值10例。凡是例题中需要理论的就讲透;凡是找不到直接需求的即予删除;凡是能找到简明证法的尽量从简。教材要充分利用成熟的MATLAB资源,尽量把理论与所用到的子程序衔接起来,使学生不至于傻瓜式的用软件。我们的目标是把课程改造得能为工科大一学生以及在职工程师所接受,全国这一群体有几千万人,因此尽量做到浅显易懂。
我们有一篇专文 [5] 详细地介绍了简化内容的根据和详情,此处只简单地谈一下:
1) 把高斯消元法解线性方程组作为全书的理论主线,把行列式、秩、乃至向量线性相关性等都纳入这根主线上,使理论单一化。本书中,行阶梯变换(MATLAB函数rref)的使用频度是很高的,既用来解方程组,又用来定义行列式,和求向量组相关性和秩。
2) 极大地削弱了行列式。因为除了低阶行列式表示面积体积外,高阶行列式没有物理意义,在工程中找不到计算需求。两种经典行列式定义方法都无可计算性,故代之既简单又好算的主元连乘定义。行列式性质本来是为其计算服务的,计算简单了,性质也省了好多。我们也曾怀疑是不是删掉太多了?但是拿国外教材及MATLAB一比,发现我们删掉的内容(如行列式按行展开、随伴矩阵等),也正是MATLAB中没定义也不给子程序的,几本国外著名教材都对行列式的工程意义做了负面的评述,更坚信我们的处理方法没问题。
3) 着重二、三维空间,不涉及N维向量空间;因为大一学生能搞清三维就不错了,同时也找不到N维空间在工程系本科的应用需求。
4) 弱化欠定,加强超定。欠定方程组是由于命题条件不足造成的,工程师解这类题的方法应该是挑出题错,改正命题。欠定方程的基础解系不符合唯一性,又没有本科后续课的应用实例。要求大一学生普遍掌握既无可能,也不必要。超定方程则是工程上常见的问题,在大数据的处理中很有用处,应该使学生有初步的认识。
采用了这些改革措施后,无用的理论大大减少,有用的理论有所增加,概念题和证明题大大缩减;但解决实际问题的能力却有了长足的提高,这正是我们期待的。
5. 结论
为了证明上述“三化”可以融合为一体,我们于2014年8月写成了一本名为《实用大众线性代数(MATLAB版)》的教材(厚150页),并于2016年9月制成同名慕课,上网播放 [6] 。两年来已播四期,有四万余学生听课,得到了广泛的好评。
实施本书预计约需36学时(包括MATLAB),适合低学时的大纲。由于本书的内容和传统的教材差别太大,删掉的内容多是考研需要的,增加的内容(MATLAB和工程应用)又超出了现有数学老师的知识领域,在现有的教学计划(不论是高学时或低学时)内来实施都有难度。慕课的出现使我们“绝路逢生”。首先,教师的问题解决了;第二,跳出了学校陈旧固化的教学计划,可以大量增加现代和创新的知识;第三,学生来源的多样性使我们能得到很广泛的反馈。从2016年9月以来的两年中,注册本慕课的共有四万多人,在“课程评价”中,数以百计的读者留言给予了高度的肯定(5级分的4.8分)。摘几条如下:
“用计祘机和数学软件求解矩阵问题对非数学专业的学生是非常适用的。因为他们不需要像数学专业学生那样严格地进行数学推导和逻辑推理,他们更重视运祘速度和计祘的准确性”。
“老师注重了非数学系学生的应用特点,强调计算机对于解决实际问题的作用,这让人很受益”。
“学了多年数学,最后走向社会参加工作后,用的最多的还是加减乘除,线性代数很少用,原因就是用不上,列出式子也解不出来。自从学了这门实用大众线性代数,感觉对应用数学有了新的感觉”。
“此次的线性代数课程是本人接触过的最有价值的基础课程,很是对自己的胃口”。
“工程数学立足实践,让人会用才是根本。毫不夸张的说,这门课为我开启了一个新世界”。
“以前我真的不知道线性代数是用来干嘛的。上了这门课之后,我才知道,原来线性代数可以变成研究各个学科的利器,尤其老师讲到取代梅森公式,我简直是目瞪口呆,殊不知读书的时候被梅森公式折磨的有多惨,数闭环数到眼花想吐,用矩阵建模居然这么轻松就解决了”!
“相逢恨晚!之前从未听过如此实用‘接地气’的线性代数,作为机械工程从业者对老师表示感谢”。
“……”
在其他线性代数慕课中,学生评价都只限于老师讲课的好坏,见不到对课程应用价值的讨论。说明本慕课使学生提高了评价课程的眼光和层次。
我们认为,基础课应该是为大学生本科课程服务的。《实用大众线性代数》为学生提供了MATLAB入门,又为多门后续课提供了建模方法,所以是当之无愧的必修基础课。经典线性代数的内容,如果对本科后续课程有帮助,可以保留。如果只是为考研,放在大一就不合适,因为它浪费了大多数不考研学生的时间和精力。而且离考研还有三年,不如在大四专为考研学生开选修课来得有效。
实践证明,利用慕课,把线性代数的基本内容转移到实用的工程轨道上来,是可能的。首先应该通过慕课培养师资,2010年,我们曾按高教司的指示,为推广MATLAB和矩阵建模,办一星期的师资培训班,费了很大的劲,才培训了几十人。今天有了慕课这个工具,利用网络,培训几万人都没问题。而且不受时间空间的限制,在Mathworks公司支持下,还提供免费的在线MATLAB软件。我们可以在现有慕课的基础上,提高习题和考题的难度以培训教师。对于学生,可以先用慕课上课,本地老师辅导,逐渐由本地老师出补充和考题,实现课程的本地化。如果有学校愿意进行这样的试点,欢迎和我们联系。
文章引用
陈怀琛,杨威. 工科线性代数必需的三项改革—介绍《实用大众线性代数(MATLAB版)》教材及其慕课
Three Necessary Reforms in Linear Algebra for Engineering—Introduction to Book “Applied Linear Algebra with MATLAB”[J]. 应用数学进展, 2018, 07(09): 1159-1165. https://doi.org/10.12677/AAM.2018.79135
参考文献
- 1. 陈怀琛. 实用大众线性代数(MATLAB版) [M]. 西安: 西安电子科技大学出版社, 2014.
- 2. 陈怀琛. MATLAB及在理工课程中的应用指南[M]. 西安: 西安电子科技大学出版社, 2000.
- 3. 陈怀琛, 吴大正, 高西全. MATLAB及其在电子信息课程中的应用[M]. 北京: 电子工业出版社, 2002.
- 4. 陈怀琛, 龚杰民. 线性代数实践及MATLAB入门[M]. 北京: 电子工业出版社, 2005.
- 5. 陈怀琛, 高淑萍. 论非数学专业线性代数的内容改革[J]. 高等数学研究, 2015, 18(2): 8-11.
- 6. 陈怀琛, 杨威. 实用大众线性代数(MATLAB版) [EB/OL]. 西安电子科技大学, 中国大学MOOC (慕课). http://www.icourse163.org/course/XIDIAN-1001775006, 2018.
