Advances in Applied Mathematics
Vol.
08
No.
01
(
2019
), Article ID:
28456
,
14
pages
10.12677/AAM.2019.81006
A Stock Price Dynamic Model with Reverse Parameter and General Function of Belief
Yanxia Xu, Ke Shi, Zhenghong Pan
College of Mathematics and System Science, Xinjiang University, Urumqi Xinjiang

Received: Dec. 19th, 2018; accepted: Jan. 8th, 2019; published: Jan. 15th, 2019

ABSTRACT
In this paper, a general function of expectation beliefs based on stock price deviation is introduced to the chartists. And considering the influence of the reverse investors, we add the reverse parameter, which represents the proportion of the reverse investors in the chartists. Using difference equation to analyse the equilibrium solutions, stability and bifurcations of the system with general beliefs function, we discuss the influence of main parameters. Through analysis, it is verified that the reverse investors has an important role in the market.
Keywords:A General Function of Beliefs, Reverse Parameter, Stability, Bifurcation
含逆风参数和一般信念函数的价格动态模型
徐燕霞,师恪,潘正红
新疆大学,数学与系统科学学院,新疆 乌鲁木齐

收稿日期:2018年12月19日;录用日期:2019年1月8日;发布日期:2019年1月15日

摘 要
本文对图表分析者引入基于价格偏差的一般预期信念函数,将模型一般化。考虑到逆风者在市场中的影响,从而引入逆风参数(逆风参数指逆风者在图表分析者中所占的比例)。根据差分方程理论知识,分析了一般信念函数下系统的平衡解、稳定性、分支等,并讨论了主要参数对系统稳定性的影响。通过分析,验证了逆风者具有稳定市场的作用。
关键词 :一般信念函数,逆风参数,稳定性,分支

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来更多的资本资产定价模型(CAPM)强调信念的异质性,即不同交易者关于未来价格有不同的预期信念。Zeeman (1974) [1] 是较早用异质交易者模型来解释经济市场动态的文章,随后许多学者通过假设市场中含有不同类型的投资者来建立市场定价模型。Brock and Hommes (1998) [2] 是最具有影响力的异质信念资产定价模型,文中建立了一个两类交易者的自适应信念系统,投资者根据不同的预测策略选择适应度函数去预测价格,并通过观测过去已实现的收益调整他们的交易策略,投资者都是有界理性的,更愿意将策略转换到上一时期收益较高的策略中,且文中考虑图表分析者的信念为线性函数。Gaunersdorfer and Hommes (2000) [3] 建立了关于价格偏差的价格预期函数。在Ding等(1993) [4] 中用一个简单的带异质信念的资产定价模型研究记忆对进化适应度的影响。
异质资产定价模型中,由于进化选择由短期效用所控制,所以非理性图表分析者是可以存在的。Beja and Goldman (1980) [5] 建立了一个线性的交易者策略,分析了市场均衡点的稳定性受到追风者比例的影响,追风者比例越高,市场均衡越不稳定。王铎(2004) [6] 在前人的基础上考虑了图表分析者持非线性预期信念,研究了图表分析者的学习强度对系统稳定性的影响。Miroslav Verbic (2012) [7] 在文献 [2] 的基础上考虑记忆对适应度函数的影响,发现记忆参数使得市场产生微小波动,影响市场中基本面分析者的主导地位,并且记忆会通过限定选择强度的区间来影响它的稳定性。Cars and Tatiana (2012) [8] 研究了常数记忆参数对价格动态的影响,考虑了累积权重 和标准权重 两种情形,发现记忆参数为累积权重时对系统稳定状态的影响大于标准权重的情形。
胡建梅(2013) [9] 将逆风参数引入到资产定价模型中,分析了逆风参数对稳定区域及价格波动的影响,发现逆风参数可以起到稳定市场的作用。张艳萍(2016) [10] 同时对于顺风者和逆风者考虑一类受价格波动性影响的非线性价格预期函数建立资产定价模型。Chiarella and He (2002) [11] ,Beum-Jo Park (2014) [12] 对图表分析者引入时变异质风险厌恶系数,认为不同的交易者对风险所持的态度不同。Brock and Hommes (2002) [13] ,He and Li (2015a) [14] ,He and Li (2015b) [15] 在一个简单的含有异质交易者的市场分数模型中,通过系统选择模型的一系列结构参数,利用Monte Carlo模拟做计量经济学分析,描述了收益序列的一些程式化事实。在文献 [2] 的升级资产定价模型中,异质有界理性交易者在固定数量的预测规则之间进行选择,但交易者的异质性是限定在经典的技术分析和基本面分析规则之间进行转换。Jan Polach (2018) [16] 对模型引入了非线性函数,考察了参数对预期价格的影响。Schmitt,Noemi (2018) [17] 推广了他们的框架,考虑了所有的交易者跟随他们自己的时变的基本面分析和技术分析预测规则,通过联合力矩覆盖率,发现模型显著性的关键是假设各交易者的预期是异质的。
受到文献 [6] 和文献 [9] 的启发,这里在文献 [17] 的基础上,对图表分析者的信念考虑关于价格偏差的一般信念函数,并引入逆风参数k,进而建立含三类交易者(即基本面分析者、顺风者、逆风者)的资产定价模型,根据差分方程理论知识,分析了一般信念函数下系统的平衡解、稳定性、分支等,并讨论了主要参数对系统稳定性的影响。验证了逆风者具有稳定市场的作用。
2. 建立模型
2.1. 模型的假设
本文模型依据Schmitt,Noemi (2018) [17] 建立的。考虑一个具有一种风险资产和一种无风险资产的金融市场,其中无风险资产是弹性供应的,年利率为r,风险资产是零净供应的,随机股息过程 为独立同分布的,均值为 。定义 为t时点每股风险资产的价格, 为t时点购买风险资产的股份数目,则 时点的财富动态为
令 和 分别表示投资者h的条件期望和条件方差。假定投资者都是均值-方差最大化者,即
这里,a为常数风险厌恶系数。h类投资者对风险资产的需求函数 为
令 表示投资者的风险外股票供应量, 为t时点交易者h的市场分数,市场供需均衡意味着
假定条件方差为常数,且对所有的投资者都有 ,则均衡定价方程为
如同文献 [2] ,这里考虑外部供应为零的情形,即 。风险资产的基本价格由预期股息的贴现和供给给出,为
定义价格偏差为
则投资者的价格预期信念为
表示投资者对价格偏离基本价格的信念。则得到定价方程为:
2.2. 交易者的预期信念函数
基本面分析者假设知道基本价格 的相关信息,并且他们认为价格短时间内会偏离基本价格,但长时会均值回馈到基本价值。考虑基本面分析者持线性期规则,
这里, 为均值回归系数,当 时表示纯粹的基本面分析者,他们对下一期的价格预期为基本价格。
图表分析者通过近期的历史价格趋势推断形成他们的交易策略。受王铎启(2004)发,本文对图表分析者引入关于价格偏差的一般信念函数,即
其中, ,为图表分析者的趋势推断参数, 表示顺风者, 表示逆风者。对一般函数 ,设它在初始点 处存在直到n阶的导数,则有
(1)
则
其中,根据Cars and Tatiana (2012) [8] ,考虑记忆对市场分数的影响,则
这里记忆参数 ,为实数。
对适应度函数引入累计权重,即 , 为实数,则
令 ,已实现的收益为
令 为市场分数差,则
令 , ,根据胡建梅(2013) [9] ,本文对逆风者引入逆风参数k,即逆风者在图表分析者中所占的比例为 ,则顺风者所占比例为 ,资产定价方程可写为
(2)
得到下面的非线性离散随机动力系统
(3)
令 ,通过增维降阶动力系统变为:
(4)
3. 系统平衡点,稳定性及分支的讨论
引理 对常系数线性差分方程组
1) 若矩阵A所有特征根的模都不大于1,且模等于1的模是单重根,则线性差分方程组的零解是稳定的;
2) 若矩阵A所有特征根的模小于1,则线性差分方程组的零解是渐进稳定的;
3) 若矩阵A有模大于1的特征根,则线性差分方程组的零解是不稳定的。
定理1 假设函数 满足 ,且 。令 ,且 ,则 为系统(3)的基本平衡解。
3.1. 基本面分析者主导市场时模型分析
当 ,即图表分析者中顺风者与逆风者占比相同时,模型退化为
(5)
此时,顺风者与逆风者在图表分析者中的占比相同,导致图表分析者在市场中的影响变弱,市场由基本面分析者主导。
这里要么 ,要么 ,进一步得到基本平衡点,此时价格等于基本价值,且市场分数
差为:
由(4)中的第四个式子可以得到 , 。平衡点的市场分数差为:
(6)
其它非基本平衡点满足
其中
则
进一步化简得到
(7)
定理2 当 时,基本平衡解 是系统(5)唯一的平衡解,记忆参数 , 对平衡点的位置有影响。
证明 由于 , ,则 成立,且表达式 成立。但事实上,双曲正切
函数的值在 之间,故表达式(7)没有解,则基本平衡解 是系统(5)唯一的平衡解。由于在(6)式中有记忆强度参数 , ,故记忆会影响平衡解的位置。
3.2. 一般情况下模型分析
下面讨论一般情况下平衡解的稳定性。令 ,模型的确定性系统可以定义为 ,即
(8)
其中
令 为系统的平衡解,它满足 ,即满足下列方程组:
(9)
定理3 假设函数 满足 ,使得 (当且仅当 时, ),且 成立,则系统有基本平衡解 和非零平衡解 。这里 。非零平衡解 若存在,则有
1) 当 时,系统有基本平衡解 和非零平衡解 ,其中
2) 当 时,系统有基本平衡解 和非零平衡解 ,其中
3) 当 时,系统只有基本平衡解 。
证明 对于方程组(9)中的第一个式子
可以得到
由于 , , , , ,则 。
1) 当 时, ,则 ,故 ,记为 。此时系统有基本平衡解 和非零平衡解 ,其中 。
2) 当 时, ,则 ,故 ,记为 。此时系统有基本平衡解 和非零平衡解 ,其中 。
3) 当 时,系统只有基本平衡解 ,证明过程由定理1可得。
定理4 (基本平衡解的稳定性) 设 为系统(3)的基本平衡解,其中 , ,令 , ,则:
1) 当 ,即市场中顺风者在图表分析者中所占的比例大于逆风者时,
(i) 当 时, 是局部渐进稳定的。
(ii) 当 时,
1o、当 时, 是渐进稳定的。
2o、当 时, 是不稳定的。
3o、当 时,系统出现分支。
(iii) 当 时, 是全局不稳定的。
2) 当 ,即市场中逆风者在图表分析者中所占的比例大于顺风者时,
(i) 当 时, 是全局渐进稳定的。
(ii) 当 时,
1o、当 时, 是渐进稳定的。
2o、当 时, 是不稳定的。
3o、当 时,系统出现分支。
(iii) 当 时, 是全局不稳定的。
3) 当 时,此时平衡解 是系统唯一的平衡解,且是全局渐进稳定的。
证明 平衡点的局部稳定性由Jacobian矩阵的特征值决定,则在 处的Jacobian矩阵为
其中
这里 ; 。
则Jacobian矩阵J的特征方程为
解得特征根为 , , , 。
根据引理可知,差分系统(8)的基本平衡点稳定的充要条件是 。
而 , ,则当 时基本平衡点 是稳定的。由于
,
1) 当 时, ,即 成立,下面讨论 的情况。
此时
由上式得
(i) 当 时,有 ,则
令
1o、当 时, ,则恒有 成立,则 是渐进稳定的。
2o、当 时,要使得 成立,则
成立,解得
令
为系统的分支点,则当 时,有 。
当 时, 是渐进稳定的。
当 时, 是不稳定的。
(ii) 当 时,
1o、当 时,有 ,则 成立。
此时 ,则基本平衡解 是全局渐进稳定的。
2o、当 时,有 ,则可以得到 成立。此时 ,则基本平衡解 是全局渐进稳定的。
3o、当 时,有 ,则 。
此时,当 时, 是渐进稳定的;
当 时, 是不稳定的。
4o、当 时,有 。则 。
由于 ,此时 不成立,故 全局不稳定。
2) 当 , 成立,下面讨论 的情况,即
由上式得
由于 成立,故
令
.
1o、当 时,有 ,则 。此时, 恒成立,则 是渐进稳定的。
2o、当 时,有 ,则 。要使得 成立,则
成立,解得
令
为系统的分支点,且由 ,可得 ,则 恒成立。
故,当 时, 是渐进稳定的。
当 时, 是不稳定的。
3o、当 时,有 ,则 成立。
此时对所有的 ,都有 不成立。故 是全局不稳定的。
当 时, 成立。由于 , ,则 恒成立,即此时平衡解
是全局渐进稳定的。

Figure 1. Phase plots
图1. 相图
图1表示 的相图,它反映出投影平面上轨迹收敛于一条闭曲线,系统存在周期解,说明在分支附近平衡解虽然不稳定,但却存在吸引子,保证了系统的全局稳定性。
3.3. 主要参数对系统分支的影响
下面在确定性系统(取 )中讨论参数对系统分支的影响。
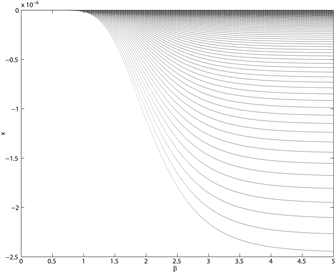
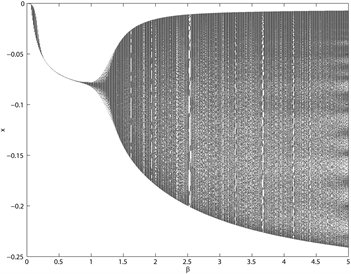
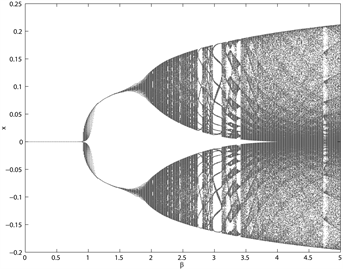
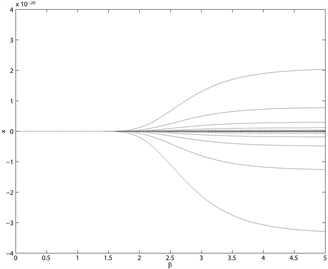
Figure 2. Bifurcation diagrams of the intensity of choice (β)
图2. 选择强度 的音叉分支
图2为选择强度 的音叉分支图,在选择强度 之前,系统的平衡解是稳定的,当超过这个临界值时,平衡解变得不稳定,系统出现分支。这里逆风参数分别取 ,发现k越接近0.5,分支越不明显。且当k的值越大时,分支出现的越迟,说明逆风者具有稳定市场的作用。
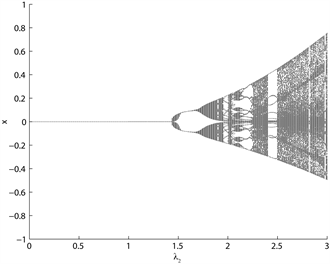
Figure 3. Bifurcation diagrams of
图3. 参数 的音叉分支图
图3为图表分析者关于趋势推断 的分支图,此时取 ,趋势推断参数 越大,分支越明显。
图4为当 时,一些主要参数对分支点 的影响示意图,其中由前文可知
。这里 关于记忆参数 是递减的,即当 增大时,过去效用对适应度
函数的影响减小,分支出现的越早,系统越不稳定。第二个图中刚开始随着逆风参数k增大, 随之增大,当k超过临界值 时,随着k增大, 减小,即当 时,k的增大具有稳定市场的作用,当 时,k的增大反而使得分支出现的越早,与图2中结论类似。参数 和 也有类似的结论。
图5为当 时,主要参数对分支点 的影响, 。 关于记
忆参数 是递增的,即当 增大时,过去效用对适应度函数的影响增大,分支出现的越迟,系统越稳定。


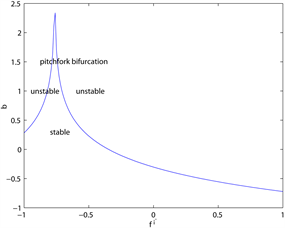
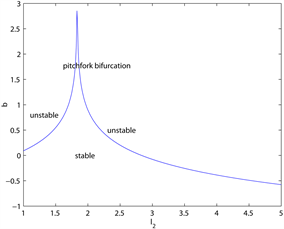
Figure 4. The effect of parameters on when
图4. 时参数对分支点 的影响
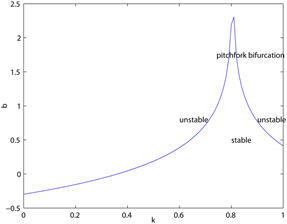
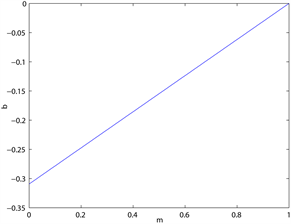
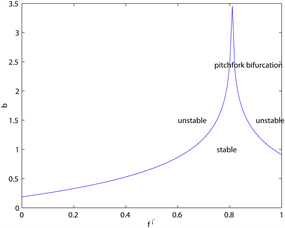
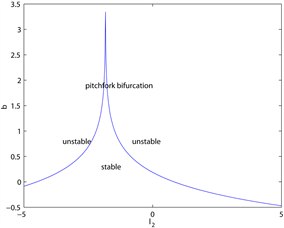
Figure 5. The effect of parameters on when
图5. 时参数对分支点 的影响
4. 总结
本文在Schmitt,Noemi (2018) [17] 的基础上,对图表分析者考虑含逆风参数和基于价格偏差的一般预期信念函数,建立了一个含三类交易者(即基本面分析者、顺风者、逆风者)的简单资产定价模型。应用差分方程理论知识,分析了一般信念函数下系统的平衡解、稳定性、分支等,并讨论了一些主要参数对系统稳定性的影响,从而验证了逆风者具有稳定市场的作用。
文章引用
徐燕霞,师 恪,潘正红. 含逆风参数和一般信念函数的价格动态模型
A Stock Price Dynamic Model with Reverse Parameter and General Function of Belief[J]. 应用数学进展, 2019, 08(01): 50-63. https://doi.org/10.12677/AAM.2019.81006
参考文献
- 1. Zeeman, E. (1974) On the Unstable Behaviour of Stock Exchanges. Journal of Mathematical Economics, 1, 39-49.
https://doi.org/10.1016/0304-4068(74)90034-2 - 2. Brock, W. and Hommes, C. (1998) Heterogeneous Beliefs and Routes to Chaos in a Simple Asset Pricing Models. Journal of Economic Dynamics and Control, 22, 1235-1274.
https://doi.org/10.1016/S0165-1889(98)00011-6 - 3. Gaunersdorfer, A. and Hommes, C. (2000) A Nonliner Structural Model for Volatility Clustering. CeNDEF Working Papers, 00-01, 265-288.
- 4. Ding, Z., Granger, C. and Engle, R. (1993) A Long Memory Property of Stock Market Returns and a New Model. Journal of Empirical Finance, 1, 83-106.
https://doi.org/10.1016/0927-5398(93)90006-D - 5. Beja, G. (1980) On the Dynamic Behavior of Prices in Disequilibrium. Journal of Finance, 35, 235-247.
https://doi.org/10.1111/j.1540-6261.1980.tb02151.x - 6. 王铎, 彭建平, 郑敏. 做市商调整价格速度与资产价格的波动[J]. 管理评论, 2004, 16(11): 28-34.
- 7. Verbic, M. (2012) Memory and Asset Pricing Models with Heter-ogeneous Beliefs. Nonlinearity, Bifurcation and Chaos-Theory and Applications, 12, 214-311.
- 8. Hommes, C. and Kiseleva, T. (2012) Is More Memory in Evolutionary Selection (De)stabilizing? Macroeconomic Dynamics, 16, 335-357.
https://doi.org/10.1017/S136510051000060X - 9. 胡建梅. 含逆风参数的两类价格动态模型及实证分析[D]: [硕士学位论文]. 乌鲁木齐: 新疆大学, 2013.
- 10. 张艳萍. 基于一类非线性价格预期函数的资产定价模型的研究[D]: [硕士学位论文]. 乌鲁木齐: 新疆大学, 2016.
- 11. Chiarella, C. and He, X.-Z. (2002) Heterogeneous Beliefs, Risk and Learning in a Simple Asset Pricing Model. Computational Economics, 19, 95-132.
https://doi.org/10.1023/A:1014957310778 - 12. Park, B.-J. (2014) Time-Varying, Heterogeneous Risk Aversion and Dynamics of Asset Prices among Boundedly Rational Agents. Journal of Banking & Finance, 43, 150-159.
https://doi.org/10.1016/j.jbankfin.2014.03.009 - 13. Brock, W. and Hommes, C. (2002) Heterogeneous Beliefs and Routes to Complex Dynamics in Asset Pricing Models with Price Contingent Contracts. In: Hommes, C.H., Ramer, R. and Withagen, C.A., Eds., Equilibrium, Markets and Dynamics, Springer, Berlin, 245-265.
- 14. He, X.-Z. and Li, Y. (2015) Testing of a Market Fraction Model and Power-Law Behaviour in the DAX 30. Journal of Empirical Finance, 31, 1-17.
https://doi.org/10.1016/j.jempfin.2015.01.001 - 15. He, X.-Z. and Li, Y. (2015) The Adaptiveness in Stock Markets: Testing the Stylized Facts in the Dax 30. Journal of Evolutionary Economics, 27, 1-24.
- 16. Polach, J. and Kukacka, J. (2018) Prospect Theory in the Heterogeneous Agent Model. Journal of Economic Interaction & Coordination, 1-28.
https://doi.org/10.1007/s11403-018-0219-6 - 17. Schmitt, N. (2018) Heterogeneous Expectations and Asset Price Dynamics.
- 18. 周义仓, 曹慧, 肖燕妮. 差分方程及其应用[M]. 北京: 科学出版社, 2014.