Advances in Applied Mathematics
Vol.
08
No.
02
(
2019
), Article ID:
28841
,
9
pages
10.12677/AAM.2019.82024
An M/M/1 Retrial Queue with Working Vacation and Feedback
Juntong Li, Tao Li, Jinping Xu
School of Mathematics and Statistics, Shandong University of Technology, Zibo Shandong

Received: Jan. 22nd, 2019; accepted: Feb. 6th, 2019; published: Feb. 13th, 2019

ABSTRACT
In this paper, we considered an M/M/1 retrial queue with working vacation and feedback. In order to obtain the necessary and sufficient condition for system to be stable, the matrix-analytic method is used. The stationary probability distribution and some performance measures were also derived. Then we give the conditional stochastic decomposition for the queue length in the orbit when the server is busy. Finally, the model parameters on the system's characteristics are presented by some numerical examples.
Keywords:Retrial, Working Vacation, Collision, Conditional Stochastic Decomposition
带有反馈的M/M/1重试工作休假排队模型
李俊潼,李涛,徐金萍
山东理工大学数学与统计学院,山东 淄博

收稿日期:2019年1月22日;录用日期:2019年2月6日;发布日期:2019年2月13日

摘 要
研究带有反馈、重试和工作休假的M/M/1排队模型:当系统为空时,服务员进入工作休假,以低速率提供服务,若顾客到达时服务员忙,则顾客进入重试组等待,接收服务完毕的顾客以概率p离开系统或以概率 返回系统重新排队。对该模型,运用拟生灭过程和矩阵几何解的方法,得到平稳队长及一些相应指标,并给出队长分解,最后,利用数值例子进行解释。
关键词 :重试,工作休假,反馈,随机条件分解

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在我们日常生活中,经常会出现拥挤堵塞的情况,比如电话占线、银行服务、交通堵塞等情况,排队论就是解决这类问题的有效工具。
在排队论的研究进程中,有关休假系统和重试系统已经被广泛研究,我们可以通过Tian和Zhang [1] 了解到一些基本模型。休假排队策略允许服务员在某些时刻不接待顾客,这些暂时停止提供服务的状态统称为休假;重试就是指当顾客到达系统时发现服务员正在工作,那么顾客就会进入到一个重试组(通常称之为orbit)等待,过一段时间之后再重新向服务员发出服务请求。关于重试的一些文献可以参考 [2] [3] [4] 。而在普通休假的基础上,Servi和Finn [5] 首次提出了工作休假的概念,并研究了带有工作休假的M/M/1模型,工作休假是指在休假过程中,服务员不完全停止服务,而是转为低速率提供服务。在此基础上,Do [6] 研究了带有重试和工作休假的M/M/1排队模型。当下,将重试和工作休假结合的模型研究已经非常广泛,一些其他有价值的结论可以参考Li et al. [7] 。在实际的应用中,顾客的行为是多样的,顾客接受服务后也可能重新回到系统再次申请服务,这种情况可以用具有“反馈”的排队系统描述。如多路的远程通讯系统,如果给用户端的消息出错,那么用户端则会向服务器重新发送一次服务请求。2002年B. Krishna Kumar等 [8] 研究了顾客有伯努利反馈、服务器有启动失败且重试时间服从一般分布的M/G/1重试排队系统。2005年Kailash C. Madan和Mohammad Al-Rawwash [9] 研究了有顾客反馈的M/G/1可选择单重休假排队系统。
本文主要研究带有反馈的M/M/1重试工作休假排队模型。采用嵌入Markov链法,给出系统存在稳态的充要条件,求出了平均队长等系统指标,此外还讨论了稳态下队长的随机条件分解,最后对给定的某些数值做出图形变换趋势及解释。
2. 模型描述
我们考虑研究带有反馈的M/M/1重试工作休假排队模型,关于模型的一些细节描述如下:
1) 顾客的到达时间服从参数为 的泊松过程。
2) 正常服务期,服务员的服务速率服从参数为 的指数分布,当重试组中没有顾客时,服务员开始一段时间为V的工作休假,且工作休假时间服从参数为 的指数分布。在工作休假期间,服务员以低速率 提供服务,且 。当一个工作休假结束,若重试组中有顾客,则开始一个新的忙期,若重试组中没有顾客,则开始一个新的工作休假。
3) 当顾客到达系统发现服务员在忙,则顾客进入重试组等待,重试组中的顾客只有排在队列最前面的才能对服务器进行重试,直到重试成功并接受服务,重试时间服从参数为 的指数分布。
4) 顾客接受服务完毕后瞬间以概率 离开系统,或以概率 返回重试组重新排队等待服务。
另外,我们假设顾客的到达时间、重试时间以及系统的休假时间、正常工作期和工作休假期的服务时间都是相互独立的。
令 表示t时刻重试组中的顾客数, 表示t时刻服务员的状态,则服务员的四个状态如下:
则随机过程 是一个以 为状态空间的拟生灭(QBD)过程。
该过程的最小生成元矩阵可以写成分块模式如下:
其中
3. 系统存在稳态的充要条件及稳态队长
定理1:QBD过程 正常返的充分必要条件是 。
证明:首先,我们假设
根据文献 [10] ,定理7.3.1,对行列式进行变换得到QBD正常返条件为:
其中e为单位列向量, 为 , 的唯一解。经过运算可得QBD的正常返条件为 。证毕。
定理2:当 时,矩阵方程 有最小非负解:
其中
证明:根据 的结构,我们假设 ,其中 , 和 都是 的矩阵。把R带入方程 中得到一系列方程
由第一个方程,我们可以得到 ,同理 可以由第三个方程解得,将 和 代入第二个方程,可以经过计算得到 。证毕。
在稳态条件下,我们有
值得注意的是,当重试组中没有顾客时,正常工作期服务员忙的概率是0,因此 。
定理3:如果 ,则QBD过程 的平稳分布由下式给出:
(1)
并且
(2)
其中 可由归一化条件求得。
证明:由
将 代入上述方程,我们可以得到(1)式。并且 满足下述方程:
(3)
通过(3)式我们可以计算得到(2)式。
再由
我们得到 。
其中
证毕。
服务员不同状态下的概率如下:
服务员忙时的概率为:
服务员闲时的概率为:
用L表示重试组中的顾客数,我们可以得到
用 表示系统中的顾客数,我们可以得到
4. 随机条件分解
引理1:如果 ,令 表示服务员忙时带有反馈和重试的M/M/1排队系统重试组中的条件队长,则 有概率母函数如下:
证明:证明过程与文献 [11] 中引理1相似,此处我们省略证明过程。
令 表示本系统orbit中服务忙时的条件队长,如果 ,我们可以得到
其中, 。
因此, 可以写成两个独立变量的和: ,其中 可以由引理1得到,并且 服从参数为 的指数分布,附加队长 也有函数 。
5. 数值例子
这一部分,在系统稳态的条件下,我们给出一些数值例子来解释平均稳态队长 和服务员忙时的概率 。在不作为研究变量的情况下,我们给变量赋值为 , , , , 。
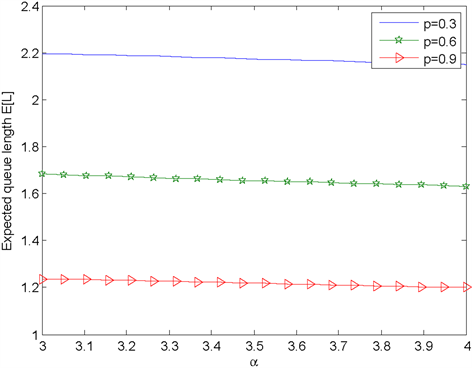
Figure 1. The expected queue length in the orbit with the change of
图1. 重试参数 对重试组队长的影响

Figure 2. The probability that the server is busy with the change of
图2. 重试时间对服务员忙时的概率的影响
图1和图2展示了 对队长 和服务员忙时的概率 的影响,随着 的增加,也就意味着重试时间减少。当服务员空闲时,到达的顾客和重试的顾客竞争接受服务,因此,重试时间越短,服务员忙的概率越大,导致 增加,而队长 减小。我们也可以看出随着p的增加队长 减小,而 则呈现相反的趋势。

Figure 3. The expected queue length in the orbit with the change of
图3. 重试参数 对重试组队长的影响
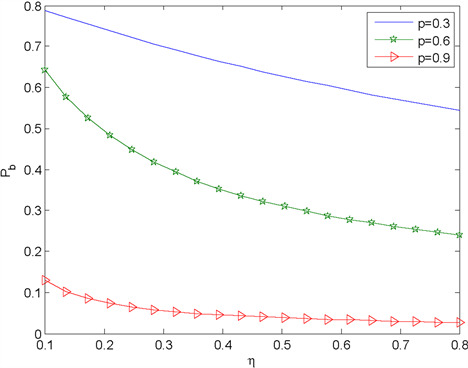
Figure 4. The probability that the server is busy with the change of
图4. 工作休假服务速率 对服务员忙时的概率的影响
在图3和图4中,我们根据不同工作休假服务速率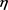 变化给出了队长
和服务员忙时的概率
的变化曲线。我们可以看到,随着工作休假服务速率
的增加,队长
和概率
都减小,原因是在工作休假期间,服务员没有完全停止工作,而是以低速率继续提供服务,导致曲线呈下降趋势。并且我们可以知道
,相当于顾客没有反馈行为,因此p越大,对系统的影响越小。
变化给出了队长
和服务员忙时的概率
的变化曲线。我们可以看到,随着工作休假服务速率
的增加,队长
和概率
都减小,原因是在工作休假期间,服务员没有完全停止工作,而是以低速率继续提供服务,导致曲线呈下降趋势。并且我们可以知道
,相当于顾客没有反馈行为,因此p越大,对系统的影响越小。
6. 结论
本文讨论了带有反馈、重试和工作休假的M/M/1排队模型,运用矩阵几何解得到系统稳态分布,以及系统稳态队长和忙期概率等指标。最后,通过数值例子分析重试以及工作休假对稳态队长和忙期概率的影响,为决策者做出决策从而使系统达到最优提供了理论依据。
文章引用
李俊潼,李 涛,徐金萍. 带有反馈的M/M/1重试工作休假排队模型
An M/M/1 Retrial Queue with Working Vacation and Feedback[J]. 应用数学进展, 2019, 08(02): 210-218. https://doi.org/10.12677/AAM.2019.82024
参考文献
- 1. Tian, N. and Zhang, Z.G. (2006) Vacation Queueing Models-Theory and Applications. Springer Link, Berlin. https://doi.org/10.1007/978-0-387-33723-4
- 2. Dragieva, V.I. (2011) Some Orbit Size Properties in the M/M/1//N Retrial Queue. International Conference on Queuing Theory & Network Applications. https://doi.org/10.1145/2021216.2021223
- 3. Dragieva, V. and Phung-Duc, T. (2017) Two-Way Communication M/M/1//N Retrial Queue. In: Thomas, N. and Forshaw, M., Eds., Analytical and Stochastic Modelling Techniques and Applications (ASMTA 2017). Lecture Notes in Computer Science, Vol. 10378, Springer, Cham. https://doi.org/10.1007/978-3-319-61428-1_6
- 4. Fedorova, E. and Voytikov, K. (2017) Retrial Queue M/G/1 with Impatient Calls under Heavy Load Condition. In: Dudin, A., Nazarov, A. and Kirpichnikov, A., Eds., Information Technologies and Mathematical Modelling. Queueing Theory and Applications (ITMM 2017). Communications in Computer and Information Science, Vol. 800, Springer, Cham. https://doi.org/10.1007/978-3-319-68069-9_28
- 5. Servi, L.D. and Finn, S.G. (2002) M/M/1 Queue with Work-ing Vacations (M/M/1/WV). Performance Evaluation, 50, 41-52. https://doi.org/10.1016/S0166-5316(02)00057-3
- 6. Do, T.V. (2010) M/M/1 Retrial Queue with Working Vaca-tions. Acta Informatica, 47, 67-75. https://doi.org/10.1007/s00236-009-0110-y
- 7. Li, T., Zhang, L. and Gao, S. (2015) An M/M/1 Retrial Queue with Bernoulli-Schedule-Controlled Vacation and Vacation Interruption. ICIC Express Letters, 9, 3385-3392.
- 8. Kumar, B.K., Madheswari, S.P. and Vijayakumar, A. (2002) The M/G/1 Retrial Queue with Feedback and Starting Failures. Applied Mathematical Modelling, 26, 1057-1075. https://doi.org/10.1016/S0307-904X(02)00061-6
- 9. Madan, K.C. and Al-Rawwash, M. (2005) On the M/G/Lqueue with Feedback and Optional Server Vacations Based on a Single Vacation Policy. Applied Mathematics and Computation, 160, 909-919.
- 10. Latouche, G. and Ramaswami, V. (1999) Introduction to Matrix Ananlytic Methods in Stochastic Modelling. ASA-SIAM Series on Applied Probability. https://doi.org/10.1137/1.9780898719734
- 11. Li, T., Wang, Z. and Liu, Z. (2012) Geo/Geo/1 Retrial Queue with Working Vacations and Vacation Interruption. Journal of Applied Mathematics Computing, 39, 131-143. https://doi.org/10.1007/s12190-011-0516-x