Advances in Applied Mathematics
Vol.
08
No.
12
(
2019
), Article ID:
33353
,
10
pages
10.12677/AAM.2019.812223
High Energy solutions of Forth-Order Elliptic Systems Involving Nonlocal Term and Sign-Changing Potential
Yawen Qian, Gao Jia
College of Science, University of Shanghai for Science and Technology, Shanghai

Received: Nov. 12th, 2019; accepted: Dec. 2nd, 2019; published: Dec. 9th, 2019

ABSTRACT
This paper focus on the following forth-order elliptic equations involving non-local terms and sign-changing potential
Where
is the biharmonic operator,
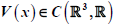 ,. is sign-changing function,
. Under certain conditions, it’s proved that there are infinitely many high-energy solutions to the problem using Fountain Theorem.
,. is sign-changing function,
. Under certain conditions, it’s proved that there are infinitely many high-energy solutions to the problem using Fountain Theorem.
Keywords:Biharmonic, Non-Local Term, Sign-Changing Potential, High-Energy Solution

带有非局部项的四阶椭圆型方程组的 无穷多高能量解的存在性
钱雅雯,贾 高
上海理工大学理学院,上海

收稿日期:2019年11月12日;录用日期:2019年12月2日;发布日期:2019年12月9日

摘 要
该文主要研究如下含变号位势和非局部项的四阶椭圆方程组
其中
是重调和算子,
,, 为变号函数,
。在满足一定条件下,利用Fountain定理证明了该问题存在无穷多高能量解。
关键词 :重调和,非局部项,变号位势,高能量解

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文将研究如下带有非局部项的四阶椭圆型方程组
(1.1)
其中
是重调和算子,
且
。
本文假设
和
满足如下条件:
(V)
且对任意
存在常数
,使得
(F1)
且存在
使得
其中
;
(F2)
对任意
一致成立,并且当
时,
;
(F3) 存在
,使得对任意
,都有
(F4) 对任意
,有
。
Lazer-McKenna在 [1] 中指出,四阶椭圆问题与悬索桥中的周期振动和行波等问题密切相关。近年来,许多学者广泛研究了四阶椭圆方程非平凡解的存在性和多重性,见文献 [2] [3] [4]。Kirchhoff模型考虑了由于弹性弦横向振动引起弦长度变化的因素。最近十年,Kirchhoff类型的问题更是受到许多学者的重视,并得到了大量重要的结论,见文献 [5] [6] [7]。特别地,Wu在 [8] 和 [9] 中研究了一个带有非局部项的方程组问题,并得到了该问题具有无穷多高能量解。受到以上文献的启发,在本文中我们将研究问题(1.1)并得到其存在无穷多高能量解。
本文主要结论如下:
定理1.1:假设条件(V)、(F1)~(F4)成立,则问题(1.1)存在无穷多高能量解。
符号:在本文中,我们用↪和↪↪分别表示连续嵌入和紧嵌入,用→和⇀分别表示强收敛和弱收敛,
表示合适的正常数。
2. 变分框架与预备引理
定义Hilbert空间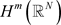 及该空间的内积为
及该空间的内积为
和
并赋予范数
由条件(V)知,存在常数
,使得对任意
,都有
。
下面定义空间
其范数定义为
对任意的
,在
上内积和范数分别定义为
和
设
,则对任意
,有
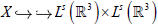 。令
。令
(2.1)
根据文献 [10] 中引理2.2知
,结合假设(V)和(F1)知泛函
。
对任意
,有
(2.2)
由变分理论知,泛函
的临界点即为问题(1.1)的弱解。
定义2.1:序列
被称为
序列当且仅当
满足:当
时,有
且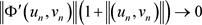 。若泛函
对应的任意
序列都有X中的强收敛子列,则称泛函
满足
条件。
。若泛函
对应的任意
序列都有X中的强收敛子列,则称泛函
满足
条件。
引理2.2:若假设(V)、(F1)成立,则泛函
对应的任意有界
序列都有强收敛子列。
证明:令
为泛函
的任一有界
序列,则有
(2.3)
由于
,则在X中存在弱收敛子列,不妨仍记为
。因此存在
,使得
(2.4)
通过计算可得
(2.5)
由(2.3)和(2.4)知
由
知,当
时,有
(2.6)
注意到,对于任意的
,有
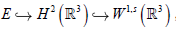 ,因此
,因此
(2.7)
结合(2.3)、(2.4)和(2.7)知,当
时,有
(2.8)
根据(2.4)以及Hölder不等式知,当
时,有
(2.9)
由(F1)、(2.4)和Hölder不等式得
(2.10)
综合上述讨论可以得到,在E中有
。类似可以得到,在E中有
。证毕。
引理2.3:假设条件(V)、(F1)、(F3)~(F5)成立,则泛函
的任意
序列都有界。
证明:令
并且满足
(2.11)
用反证法。若当
时,
,则令
,显然
。
则在X中存在弱收敛子列(不妨仍记为
)和
,使得
利用(F3)、(2.1)、(2.2)及(2.11),有
. (2.12)
显然,从上式可得
。设
,故
。对
,当
时,有
。由(F2)知,对于
,有
由Fatou引理知
(2.13)
因此,利用(2.11)和(2.13)式,条件(F1)、(F4)及
可得
(2.14)
显然上式是矛盾的。因此
在X中有界。证毕。
下面引理是证明定理1.1的主要依据。
引理2.4 (Fountain定理):设H是一个实Banach空间,并且
,对任意的
,有
。令
设
是一个偶泛函。若对任意的
,都存在
,使得
;
;
对任意 ,
满足
,
满足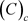 条件;
条件;
则
存在无界临界值序列。
3. 定理1.1的证明
令
是E的一组正交基,定义 ,则
。
,则
。
那么我们有下面的引理:
引理3.1:若条件(V)成立,则对
,当
时,有
(3.1)
证明:由
知,
。因此,存在
,使得当
时,有
。对每一个
,都存在
,使得
且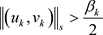 。由
的定义知,在E中
。再由Sobolev嵌入定理知,对
,有
于
。同理可得对
,有
于
。因此,当
时,有
。证毕。
。由
的定义知,在E中
。再由Sobolev嵌入定理知,对
,有
于
。同理可得对
,有
于
。因此,当
时,有
。证毕。
引理3.2:假设条件(V)、(F1)成立,则存在
,使得当
时,有
。
证明:由(2.1)和(F1)知,对任意
,有
(3.2)
根据引理3.1知
因此
由于当
时,有
,结合引理3.1知,存在
,使得当
时,有
故当
时,有
取
,由引理3.1知,当
时,有
。这样,若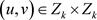 且
,则当时
,有
且
,则当时
,有
证毕。
引理3.3:假设条件(V)、(F1)、(F3)成立,则存在
,使得
。
证明:根据有限维空间的范数等价性知,对任意
,存在
,使得
(3.3)
由(F2)知,对任意的
,都存在
,使得对任意
,有
由(F1)知,当
且满足
时,有
故对任意
,有
. (3.4)
于是,由(2.1)、(3.3)、(3.4)以及Hölder不等式知,对任意的
,有
取
则存在
,使得当
且满足
时,都有
。证毕。
定理1.1的证明:显然
,由(F4)可得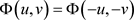 。引理2.2、2.3、3.2和3.3保证了泛函满足Fountain定理的所有条件,因此,问题(1.1)存在无穷多高能量解。
。引理2.2、2.3、3.2和3.3保证了泛函满足Fountain定理的所有条件,因此,问题(1.1)存在无穷多高能量解。
文章引用
钱雅雯,贾 高. 带有非局部项的四阶椭圆型方程组的无穷多高能量解的存在性
High Energy solutions of Forth-Order Elliptic Systems Involving Nonlocal Term and Sign-Changing Potential[J]. 应用数学进展, 2019, 08(12): 1943-1952. https://doi.org/10.12677/AAM.2019.812223
参考文献
- 1. Lazer, A.C. and McKenna, P.J. (1990) Large-Amplitude Periodic Oscillations in Suspension Bridges: Some New Connections with Nonlinear Analysis. SIAM Review, 32, 537-578.
https://doi.org/10.1137/1032120
- 2. Alexiades, V., Elcrat, A.R. and Schaefer, P.W. (1980) Existence Theorems for Some Nonlinear Fourth-Order Elliptic Boundary Value Problems. Nonlinear Analysis: Theory, Methods & Applications, 4, 805-813.
https://doi.org/10.1016/0362-546X(80)90080-2
- 3. Yin, Y. and Wu, X. (2011) High Energy Solutions and Nontrivial Solutions for Fourth-Order Elliptic Equations. Journal of Mathematical Analysis and Applications, 375, 699-705.
https://doi.org/10.1016/j.jmaa.2010.10.019
- 4. Ferrero, A. and Warnault, G. (2009) On Solutions of Second and Fourth Order Elliptic Equations with Power-Type Nonlinearities. Nonlinear Analysis: Theory, Methods & Applications, 70, 2889-2902.
https://doi.org/10.1016/j.na.2008.12.041
- 5. 张粘, 贾高. 一类带有非局部项的四阶椭圆方程无穷多高能量解的存在性[J]. 山东大学学报(理学版), 2019, 54(6): 81-87.
- 6. Zhang, J., Tang, X., and Zhang, W. (2014) Existence of Multiple Solutions of Kirchhoff Type Equation with Sign- Changing Potential. Applied Mathematics and Computation, 242, 491-499.
https://doi.org/10.1016/j.amc.2014.05.070
- 7. Li, Q. and Wu, X. (2014) A New Result on High Energy Solutions for Schrödinger-Kirchhoff Type Equations in . Applied Mathematics Letters, 30, 24-27.
https://doi.org/10.1016/j.aml.2013.12.002
- 8. Wu, X. (2012) High Energy Solutions of Systems of Kirchhoff-type Equations in . Journal of Mathematical Physics, 53, 1-18.
https://doi.org/10.1063/1.4729543
- 9. Zhou, F., Wu, K. and Wu, X. (2013) High Energy Solutions of Systems of Kirchhoff-type Equations on . Computers & Mathematics with Applications, 66, 1299-1305.
https://doi.org/10.1016/j.camwa.2013.07.028
- 10. Chen, S., Liu, J., and Wu, X. (2014) Existence and Multiplicity of Nontrivial Solutions for a Class of Modified Nonlinear Fourth-Order Elliptic Equations on . Applied Mathematics and Computation, 248, 593-601.
https://doi.org/10.1016/j.amc.2014.10.021


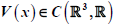 ,. is sign-changing function,
. Under certain conditions, it’s proved that there are infinitely many high-energy solutions to the problem using Fountain Theorem.
,. is sign-changing function,
. Under certain conditions, it’s proved that there are infinitely many high-energy solutions to the problem using Fountain Theorem.





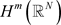 及该空间的内积为
及该空间的内积为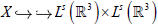 。令
。令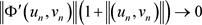 。若泛函
对应的任意
序列都有X中的强收敛子列,则称泛函
满足
条件。
。若泛函
对应的任意
序列都有X中的强收敛子列,则称泛函
满足
条件。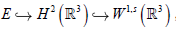 ,因此
,因此 ,
满足
,
满足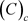 条件;
条件; ,则
。
,则
。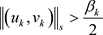 。由
的定义知,在E中
。再由Sobolev嵌入定理知,对
,有
于
。同理可得对
,有
于
。因此,当
时,有
。证毕。
。由
的定义知,在E中
。再由Sobolev嵌入定理知,对
,有
于
。同理可得对
,有
于
。因此,当
时,有
。证毕。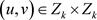 且
,则当时
,有
且
,则当时
,有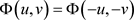 。引理2.2、2.3、3.2和3.3保证了泛函满足Fountain定理的所有条件,因此,问题(1.1)存在无穷多高能量解。
。引理2.2、2.3、3.2和3.3保证了泛函满足Fountain定理的所有条件,因此,问题(1.1)存在无穷多高能量解。