Advances in Applied Mathematics
Vol.
09
No.
02
(
2020
), Article ID:
34223
,
9
pages
10.12677/AAM.2020.92021
Series Theory of Heterogeneous Complex Variable Function
Yanhui Yang1, Yujie Jiang1, Jicheng Tao2
1Department of Information and Computer Sciences, China Jiliang University, Hangzhou Zhejiang
2Department of Mathematics, China Jiliang University, Hangzhou Zhejiang

Received: Jan. 30th, 2020; accepted: Feb. 12th, 2020; published: Feb. 19th, 2020

ABSTRACT
In this paper, the series theory of complex variable function is applied to heterogeneous complex variable function. The convergence region and the radius of convergence ellipse of heterogeneous power series are established by using the theory of heterogeneous analytic function. At the same time, the Taylor’s theorem of heterogeneous analytic function is established by using the heterogeneous Cauchy integral formula and the high order derivative formula of Cauchy integral.
Keywords:Heterogeneous Power Series, Radius of Convergence Ellipse, Taylor’s Theorem of Heterogeneous Analytic Function

非均匀复变函数的级数理论
杨彦晖1,江宇婕1,陶继成2
1中国计量大学信息科学系,浙江 杭州
2中国计量大学应用数学系,浙江 杭州

收稿日期:2020年1月30日;录用日期:2020年2月12日;发布日期:2020年2月19日

摘 要
本文把复变函数的级数理论 [1] [2] [3] 推广到非均匀复变函数上,运用非均匀解析函数理论建立了非均匀幂级数的收敛域和收敛椭圆半径,同时利用非均匀Cauchy积分公式和Cauchy积分的高界导数公式建立了非均匀解析函数的泰勒定理。
关键词 :非均匀幂级数,收敛椭圆半径,非均匀泰勒定理

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
作者们在文献 [4] [5] 推广了复变函数理论,建立了非均匀复变函数理论,给出了非均匀复数域,非均匀解析函数和非均匀积分的定义,在此基础上建立了非均匀拉普拉斯方程与非均匀Cauchy-Riemann方程组的关系,获得了非均匀Cauchy积分定理,Cauchy积分公式。随后在文献 [6] 中建立了非均匀拉普拉斯方程与非均匀解析函数的关系。因此本文利用复变函数 [4] [5] 中的理论推广文献 [1] [2] [3] 的级数理论,建立非均匀级数理论,另外,该论文的后续研究工作可以进一步研究有关非均匀复变函数理论的可视化问题 [3]。
2. 预备知识
下面给出非均匀复数、非均匀复变函数的一些基本定义及性质,具体参考文献 [4] [5]。
2.1. 非均匀复数的定义
本文考虑到复数在各个领域的广泛应用,我们对复数单位做进一步推广,定义非均匀复数。
定义集合 ,其中 为实数R, 。
在 中引入数乘
在 中引入加法
定理2.1. [4] :在上式数乘和加法运算下, 为R上的一个线性空间。
定理2.2. [4] :在上面的数乘、加法和乘法运算下, 为R上的一个域,称为非均匀复数域。
2.2. 非均匀复变函数的定义及性质
非均匀复变函数的定义,类似于复变函数的定义,形式上和数学分析中函数定义相同,此时自变量和函数的取值均为新定义的非均匀复数。在定义函数之前,根据复平面点集的几个基本概念,我们可以推广到非均匀复平面上。
定义2.3. 由 由不等式所确定的平面点集(简称点集),就是以 为圆心,以 为半径的圆,称为点 的 邻域。
注2.4. 考虑点集E,同样也有聚点或极限点、孤立点、外点、闭集、内点、开集、边界点、边界的概念,与复变平面定义相同,在此不再一一赘述。
定义2.5. 设f:从 到 的映射,则称为f为 上的非均匀复函数。
非均匀函数的导数,解析的定义及与偏微分方程组的关系在文献 [1] 中给出,下面直接给出结论不予证明:
定义2.6. 设函数 在点 的邻域内或者包含 的区域D内有定义,考虑比值
如果当z按照任意方式趋于 时,即当 按照任意方式趋于0时,比值 的极限都存在,且其值有限,则称此极限为函数 在 的导数,并记为 ,即
这时称函数 于点 可导。
定义2.7. 如果函数 在区域D内可微,则称 为区域D内的解析函数,或称函数 在区域D内解析。函数在某点解析,是指在该点的某一个邻域内是解析的:函数在某个闭域解析,是指在包含该闭域的某区域内解析。
定理2.8. [4] [5] :设函数 在区域D内解析,则
1) 偏微分 在区域D内连续;
2) 在区域D内满足非均匀C.-R.方程。
这也是可微的充要条件。
其中非均匀C.-R.方程为: 。
2.3. 非均匀复变函数的积分
非均匀复变函数的积分见文献 [5]。
定义2.9. 设非均匀复数域 上的有向曲线C:
以 为起点, 为终点, 沿C有定义,顺着C从a到b的方向在C上取分点: ,这样可以将曲线C划分为n个弧段,在从 到 的每一个弧段上任取一点 ,那么
当分点增多时,弧段逐渐加细,如果和数 极限存在且为S,则称 沿C (从a到b)可积,S为其上的积分,记号为 ,其中C为积分路径。
定理2.10. [5] :若函数 沿曲线C连续,则该函数沿曲线C可积,且
定理2.11. [5] :设有非均匀复数域
上的光滑曲线
: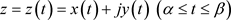 ,
,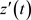 在
在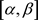 上连续且有不为零的导数
上连续且有不为零的导数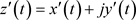 ,
,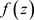 沿C连续,令
沿C连续,令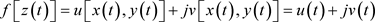 ,则有
,则有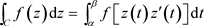 。
。
定理2.12. [5] :设函数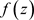 在非均匀复数域
在非均匀复数域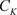 上的单连通区域D内解析,
上的单连通区域D内解析,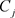 为D内任一条周线,且则有
为D内任一条周线,且则有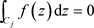 。
。
定理2.13. [5] :设函数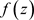 在z平面上的单连通区域D内解析,则由
在z平面上的单连通区域D内解析,则由
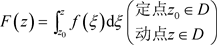
定义的函数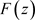 在D内解析,且
在D内解析,且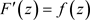 ,其中,
,其中,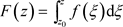 ,
,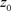 为
为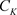 上固定点。
上固定点。
定理2.14. [5] :设区域D的边界是非均匀复数域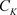 上周线(复周线)
上周线(复周线)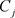 ,函数
,函数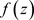 在D内解析,在
在D内解析,在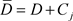 上连续,则有
上连续,则有
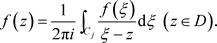
3. 非均匀复级数理论文
3.1. 非均匀复数项级数基本性质
定义3.1. 设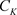 是非均匀复数域,
是非均匀复数域,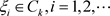 ,我们称下面的级数为非均匀复数项无穷级数
,我们称下面的级数为非均匀复数项无穷级数
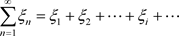 (3.1)
(3.1)
若非均匀复数列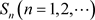 存在有限极限S,即
存在有限极限S,即 。
。
则称非均匀复数项无穷级数(3.1)收敛,且称S为级数(3.1)的和,记为
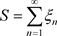
若非均匀复数列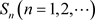 没有极限,则称非均匀级数(3.1)为发散。
没有极限,则称非均匀级数(3.1)为发散。
类似于 [2] 的证明,我们有下面的定理:
定理3.2. 设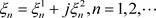 ,
,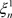 及
及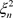 为实数,则非均匀复级数(3.1)收敛于
为实数,则非均匀复级数(3.1)收敛于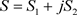 (
(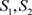 为实数)的充要条件为:实级数
为实数)的充要条件为:实级数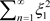 及
及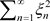 分别收敛于
分别收敛于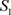 及
及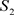 。
。
为了更好地讨论非均匀级数收敛的一些判定准则,我们提出下面非均匀模的概念:
设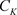 是非均匀复数域,在
是非均匀复数域,在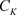 上定义非均匀模
上定义非均匀模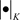 若满足下面的关系,
若满足下面的关系,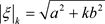 ,其中
,其中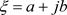 ,
,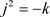 。
。
容易证明这样定义的模,三角不等式成立。
定理3.3. 非均匀复级数(3.1)收敛的充要条件为,任给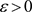 ,存在正整数
,存在正整数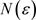 ,当
,当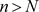 ,对于任意正整数p,有下面不等式
,对于任意正整数p,有下面不等式
 。
。
由上面不等式可知非均匀收敛级数的通项必趋于零: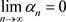 并且非均匀收敛级数的各项必然有界。
并且非均匀收敛级数的各项必然有界。
证明:令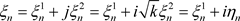 ,其中
,其中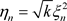 ,级数(3.1)的收敛性等价实级数
,级数(3.1)的收敛性等价实级数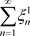 及
及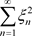 收敛,也等价与实级数
收敛,也等价与实级数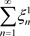 及
及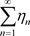 的收敛,由文献 [2] 得可西判定准则,从而获得定理3.3。
的收敛,由文献 [2] 得可西判定准则,从而获得定理3.3。
定理3.4. 若非均匀正项级数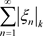 收敛,则非均匀级数(3.1)也收敛。
收敛,则非均匀级数(3.1)也收敛。
证明:由定理3.3和三角不等式结论是非常明显的。
定义3.5. 根据定理3.4可知:若非均匀正项级数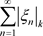 收敛,则原非均匀级数
收敛,则原非均匀级数 ,则称其为非均匀级数绝对收敛;不是绝对收敛的非均匀收敛级数,称为非均匀条件收敛。
,则称其为非均匀级数绝对收敛;不是绝对收敛的非均匀收敛级数,称为非均匀条件收敛。
3.2. 一致非均匀收敛的非均匀复函数项级数
定义3.6. 设下面的非均匀复变函数项级数的每一项在非均匀复数域 的子集E上都有定义
的子集E上都有定义
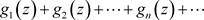 (3.2)
(3.2)
且在E上存在一个非均匀复变函数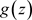 ,且任意
,且任意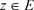 ,非均匀级数(3.2)均收敛于
,非均匀级数(3.2)均收敛于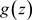 ,则称
,则称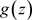 为非均匀级数(3.2)的和函数,记为
为非均匀级数(3.2)的和函数,记为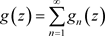 。
。
下面我们类似文献 [2] 给出一致收敛的定义:
定义3.7. 对于非均匀级数(3.2),如果在非均匀复数域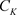 的集合E上存在一个非均匀复变函数
的集合E上存在一个非均匀复变函数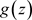 ,对任意
,对任意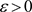 ,存在正整数
,存在正整数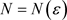 ,当
,当 时,对任意的
时,对任意的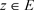 ,都有
,都有
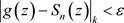 ,
,
则称非均匀级数(3.2)在E上一致收敛于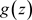 。
。
我们也有类似的柯西一致收敛准则:
定理3.8. 非均匀级数(3.2)在非均匀复数域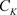 的集合E上一致收敛于非均匀函数
的集合E上一致收敛于非均匀函数 的充要条件是:任给
的充要条件是:任给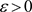 ,存在正整数
,存在正整数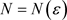 ,使当
,使当 时,对任意的
时,对任意的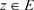 ,都有
,都有
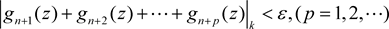 。
。
由这个准则,可得出一致收敛的优级数准则:
如果存在一列与z无关的正项数列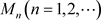 ,使对任意的
,使对任意的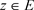 ,有
,有
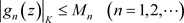 ,
,
且 收敛,则非均匀复函数项级数
收敛,则非均匀复函数项级数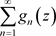 在非均匀复数域
在非均匀复数域 的集合E上绝对收敛且一致收敛:我们称级数
的集合E上绝对收敛且一致收敛:我们称级数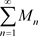 为非均匀复函数项级数
为非均匀复函数项级数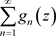 的优级数。
的优级数。
利用数学分析知识不难获得下面的定理:
定理3.9. 设非均匀复数项级数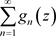 一致收敛到
一致收敛到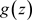 ,且
,且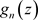 在非均匀复数域
在非均匀复数域 的集合E上连续,则和函数
的集合E上连续,则和函数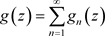 也在E上连续。
也在E上连续。
定理3.10. 设非均匀复数项级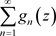 一致收敛到
一致收敛到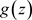 ,且
,且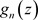 在非均匀复数域
在非均匀复数域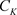 的集合E上连续,则有下面交换运算:
的集合E上连续,则有下面交换运算:
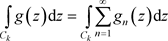 。
。
定义3.11. 设非均匀复变函数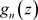 在非均匀复数域
在非均匀复数域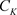 的区域D内有定义,若级数(3.2)在D内任一有界闭集上一致收敛,则称此级数在D内内闭一致收敛。
的区域D内有定义,若级数(3.2)在D内任一有界闭集上一致收敛,则称此级数在D内内闭一致收敛。
定理3.12. 非均匀复数项级数(3.2)在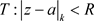 内内闭一致收敛的充要条件是任意正数
内内闭一致收敛的充要条件是任意正数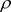 ,只要
,只要 ,级数(3.2)在椭圆闭域
,级数(3.2)在椭圆闭域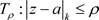 上一致收敛。
上一致收敛。
证明:必要性由定义3.11直接获得,充分性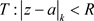 内的任意闭集K,存在充分接近正数R的正数
内的任意闭集K,存在充分接近正数R的正数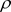 使得
使得 ,使得
,使得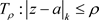 且
且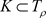 ,级数(3.2)在
,级数(3.2)在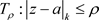 上一致收敛,由定义3.2,级数(3.2)在K上一致收敛,由定义3.11,在
上一致收敛,由定义3.2,级数(3.2)在K上一致收敛,由定义3.11,在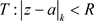 内内闭一致收敛。
内内闭一致收敛。
定理3.13. 设非均匀复数项级数的各项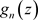 在非均匀复数域
在非均匀复数域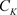 的区域D内非均匀解析且级数
的区域D内非均匀解析且级数 在D内内闭一致收敛于非均匀复变函数
在D内内闭一致收敛于非均匀复变函数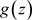 :即
:即
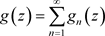 ,
,
则:1)非均匀复变函数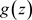 在区域D内非均匀解析;
在区域D内非均匀解析;
2)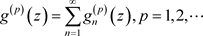 。
。
证明:1) 在区域D内任取一点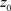 ,必存在正数
,必存在正数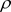 ,使得
,使得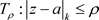 在区域D内,设C是
在区域D内,设C是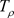 内任意一条闭曲线,而函数
内任意一条闭曲线,而函数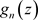 在C内非均匀解析,在C上连续,由定理2.12,我们有
在C内非均匀解析,在C上连续,由定理2.12,我们有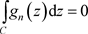 ,如是有
,如是有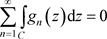 ,由定理3.10,
,由定理3.10,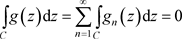 运用文献 [5] 中的定理4.5,可以得到莫雷拉定理
运用文献 [5] 中的定理4.5,可以得到莫雷拉定理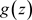 在C内非均匀解析,由C的任意性,
在C内非均匀解析,由C的任意性,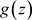 在
在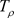 内非均匀解析,因此
内非均匀解析,因此 在区域D内非均匀解析。
在区域D内非均匀解析。
2) 利用高阶导数的非均匀Cauchy积分公式(文献 [5] 定理4.8)和等式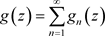 ,结论是显然的。
,结论是显然的。
3.3. 非均匀幂级数敛散性
设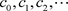 和a是非均匀复常数,我们称下面的级数
和a是非均匀复常数,我们称下面的级数
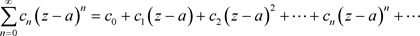 (3.3)
(3.3)
为非均匀幂级数。
我们类似文献 [2] 有下面的阿贝尔定理:
定理3.14. 如果非均匀幂级数(3.3)在点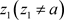 收敛,则它必在椭圆域
收敛,则它必在椭圆域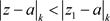 内绝对收敛且内闭一致收敛到非均匀解析函数。
内绝对收敛且内闭一致收敛到非均匀解析函数。
证明:非均匀幂级数(3.3)在点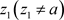 收敛,因此存在正数M,使得
收敛,因此存在正数M,使得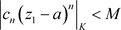 ,
,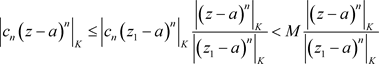 ,
,
因此,(3.3)在椭圆域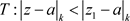 内绝对收敛。
内绝对收敛。
任取正数 ,于是任意在区域
,于是任意在区域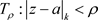 中的元素z,我们有
中的元素z,我们有
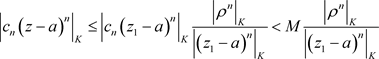
由定理3.12,(3.3)在椭圆域 内内闭一致收敛到非均匀解析函数。
内内闭一致收敛到非均匀解析函数。
下面利用阿贝尔定理给出收敛椭圆半径R的求法,即,柯西–阿达马(Cauchy-Hadamard)公式,其中收敛椭圆半径R定义为:若非均匀幂级数(3.3)在椭圆域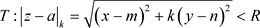 内内闭一致收敛,在
内内闭一致收敛,在 内发散,这里
内发散,这里 。
。
定理3.15. 如果非均匀幂级数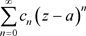 的系数
的系数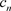 满足
满足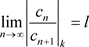 (达朗贝尔(d’Alembert))或
(达朗贝尔(d’Alembert))或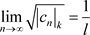 (柯西)或
(柯西)或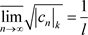 (柯西–阿达马)则幂级数
(柯西–阿达马)则幂级数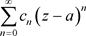 的收敛椭圆半径
的收敛椭圆半径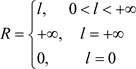 。
。
证明:我们只证第一种情况,其他情况好数学分析的证明方式一样,在此省略。令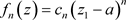 ,于是
,于是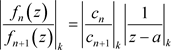 。
。
当n很大时,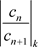 很接近l,定义椭圆域
很接近l,定义椭圆域 ,则任取一点
,则任取一点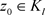 ,幂级数
,幂级数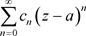 是收敛的,由阿贝尔定理可以知道在
是收敛的,由阿贝尔定理可以知道在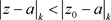 每点都内闭且一致收敛,由
每点都内闭且一致收敛,由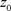 的任意性,以及在
的任意性,以及在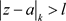 的发散性,得收敛椭圆半径为l。
的发散性,得收敛椭圆半径为l。
结合定理3.13,3.14和3.15,我们可得下面非均匀幂级数和的解析性:
定理3.16. 非均匀幂级数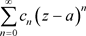 在其收敛椭圆域
在其收敛椭圆域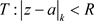 内绝对且内闭一致收敛到解析函数
内绝对且内闭一致收敛到解析函数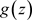 ,即
,即
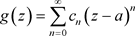 (3.4)
(3.4)
而且在T内,幂级数(3.4)可以逐项求导,即
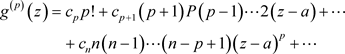 (3.5)
(3.5)
同时(3.4)和(3.5)的收敛椭圆半径R相同,其中的系数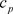 满足下面的关系
满足下面的关系
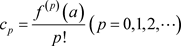 。 (3.6)
。 (3.6)
例子3.17.
1)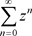 的收敛椭圆半径为1,且
的收敛椭圆半径为1,且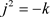 ,当
,当 ,与复变函数的理论一致,且收敛到解析函数
,与复变函数的理论一致,且收敛到解析函数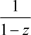 ,当
,当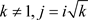 ,转化成复数项级数的形式,利用复变函数级数理论,非均匀幂级数
,转化成复数项级数的形式,利用复变函数级数理论,非均匀幂级数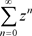 在
在 内绝对且内闭一致收敛于非均匀解析函数
内绝对且内闭一致收敛于非均匀解析函数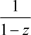 。
。
2)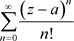 的收敛半径为
的收敛半径为 ,且如1)一样的方法可知:非均匀幂级数
,且如1)一样的方法可知:非均匀幂级数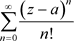 在收敛椭圆域
在收敛椭圆域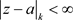 内绝对且内闭一致收敛于非均匀解析函数
内绝对且内闭一致收敛于非均匀解析函数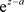 。
。
3)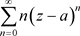 的收敛半径为0,因此除
的收敛半径为0,因此除 处处发散。
处处发散。
3.4. 非均匀解析函数的泰勒级数展开
我们在3.3节已经知道,幂级数在收敛椭圆半径内绝对且内闭一致收敛到一非均匀解析函数,本节我们讨论它的逆问题,任何非均匀解析函数是否对应一幂级数,使得非均匀解析函数与幂级数在收敛椭圆半径内收敛到的非均匀解析函数一致的。
定理3.18. 设函数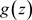 是区域D内的非均匀解析函数,
是区域D内的非均匀解析函数,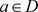 ,则只要椭圆
,则只要椭圆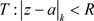 且
且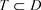 内,则
内,则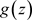 在T内能展开成非均匀幂级数:
在T内能展开成非均匀幂级数:
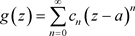 ,
,
其中系数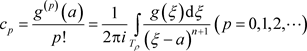 ,(
,(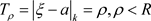 )且展开是唯一的。
)且展开是唯一的。
证明:任取一点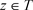 ,因此存在
,因此存在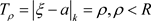 ,使得z在
,使得z在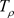 的内部。根据非均匀柯西积分公式:
的内部。根据非均匀柯西积分公式:
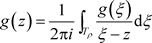 ,
,

当 在
在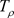 上时,
上时,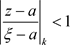 ,由例子3.17,1)
,由例子3.17,1) 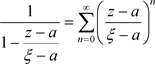
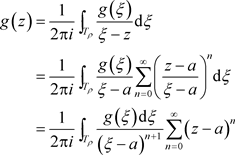
由文献 [5] 定理4.18,有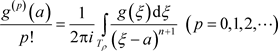 唯一性由系数的唯一性决定。
唯一性由系数的唯一性决定。
致谢
本文作者对审稿人提出的很有价值的意见表示感谢!
基金项目
中国计量大学第二十二届学生科研计划项目资助。
文章引用
杨彦晖,江宇婕,陶继成. 非均匀复变函数的级数理论
Series Theory of Heterogeneous Complex Variable Function[J]. 应用数学进展, 2020, 09(02): 178-186. https://doi.org/10.12677/AAM.2020.92021
参考文献
- 1. 李忠. 复分析导引[M]. 北京: 北京大学出版社, 2004.
- 2. 钟玉泉. 复变函数论[M]. 北京: 高等教育出版社, 2012.
- 3. 戴滨林, 杨世海. 复变函数[M]. 上海: 复旦大学出版社, 2019.
- 4. 赵雪娇, 陈雲, 陶继成. 非均匀复数和非均匀复变函数[J]. 应用数学进展, 2017, 6(1): 69-77.
- 5. 陈雲, 赵雪娇, 陶继成. 非均匀复变函数的积分[J]. 应用数学进展, 2017, 6(2): 153-164.
- 6. Tao, J.C., Chen, Y. and Zhao, X.J. (2017) Heterogeneous Complex Function. 2017 International Conference on Applied Mathematics, Modelling and Statistics Application, Beijing, China, May 22-27 2017, 345-348. https://doi.org/10.2991/ammsa-17.2017.77