Advances in Applied Mathematics
Vol.
09
No.
04
(
2020
), Article ID:
35159
,
11
pages
10.12677/AAM.2020.94062
Stochastic Dynamics Analysis of HCV Virus Model
Wang Qin*, Zhengwei Ye, Xiangling Liang, Shengwen Deng
School of Mathematics and Physic, Lanzhou Jiaotong University, Lanzhou Gansu
Received: Apr. 3rd, 2020; accepted: Apr. 14th, 2020; published: Apr. 21st, 2020

ABSTRACT
Gauss white noise was added into the nonlinear HCV model, nonlinear differential equations were established, and the original equation was reduced to a two-dimensional differential equation by applying the theorem of stochastic central manifold and the correlation theorem of stochastic average method. Then, the maximum Lyapunov index and singular boundary theory are applied to analyze the local stochastic stability and global stochastic stability of the stochastic system respectively, and the stability conditions are obtained. The dynamic bifurcation and phenomenological bifurcation behavior of systems are studied by using stochastic average method for quasi-integrable Hamiltonian systems. Finally, the numerical simulation shows that the infection rate of HCV epidemic will change obviously under the influence of noise.
Keywords:HCV Model, Hamilton Theory, Stochastic Stability, Stochastic Hopf Bifurcation

一类HCV模型的随机稳定性和分岔分析
秦旺*,叶正伟,梁相玲,邓生文
兰州交通大学,数理学院,甘肃 兰州
收稿日期:2020年4月3日;录用日期:2020年4月14日;发布日期:2020年4月21日

摘 要
在HCV模型中加入高斯白噪声,建立带有随机激励的非线性微分方程组,应用随机降阶和随机平均法相关定理将原方程化为二维的伊藤微分方程。然后,本文应用最大Lyapunov指数和奇异边界理论分析了该随机系统平凡解的局部和全局稳定性,得到了相应的稳定性条件;利用Hamilton理论中的随机平均法,对HCV系统的动态分岔和唯象分岔行为做了研究。最后,通过数值模拟得到HCV流行病在噪声的影响下传染速率会有明显的变化。
关键词 :HCV模型,Hamilton理论,随机稳定性,随机Hopf分岔

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
丙型肝炎病毒(HCV)是引起肝脏疾病的主要因素,会导致肝炎疾病的发生。估计这种慢性疾病的全球流行率已达到7100万。约60%~80%被HCV感染的患者会进展为慢性阶段,而其余患者在急性感染后可自行恢复。约15%至30%的慢性病发展为肝硬化和肝细胞癌。HCV入侵宿主后,会进入血小板,它的一些RNA会残留在血小板。此外,它可以引起血小板的自身免疫反应。文献 [1] [2] 中的模型能够解释HCV感染过程中T淋巴细胞(CTL)和免疫应答的联系。在文献 [3] 中,通过对复杂的HCV模型研究得到了树突状细胞(dc)和CTL的作用。另外,在病毒感染过程中通过对非细胞溶解治疗,HCV的自发清除也被纳入。最近,在文献 [4] 中研究了一个在无限空间传播延迟的非局部反应扩散HCV模型,以用来探究高迁移率基团盒1 (HMGB1)在阻断病毒离子方面的作用。文献 [5] 研究了乙型肝炎病毒(HBV)和乙型肝炎表面抗原(HBsAg)之间抗体对其的阻断作用。文献 [6] 研究了病毒和细胞传播和细胞介导免疫反应对于一般病毒动力学模型的影响。
文献 [7] 提出了一类传染病数学模型,其主要研究了病毒到细胞和细胞到细胞传播以及抗体应答在感染肝细胞非细胞溶解治疗中的影响。分析了该模型,讨论了确定性环境下细胞间传播和治愈率的影响。然而,由于病毒的随机行为和免疫系统的复杂性,确定性模型并不能提供对病毒动力学的充分理解。由于温度、湿度等环境参数的随机波动,在文献 [8] [9] 中提出并分析了几种基于随机方法的传染病流行模型。为了在模型分析中引入随机性,通常使用不同的方法,如参数摄动和连续时间马尔可夫链,以及加入相关的噪声。如今对于流行病的随机分析 [10] 的研究仍然很少,尤其对于丙型肝炎病毒的研究更少。
本文工作在于对HCV动力学的随机建模。因此,参考先前发表的HCV动力学确定性模型 [7],在此基础上加入白噪声对系统进行随机激励分析。首先,将带有激励的HCV模型利用降阶和平均法理论进行降阶;然后,对其平凡解的稳定性进行研究。最后,模拟分岔图验证理论的有效性。
2. 模型介绍
常见的流行病模型有SIR模型和HIV模型,除此之外,HCV模型的动力学行为也十分丰富。基于确定性的HCV模型:
(1)
方程中 和Z分别代表未感染肝细胞、感染肝细胞、病毒和b细胞的密度。这里假设 是未受感染的肝细胞固定的繁殖速率, 是未受感染的肝细胞的自然死亡速率。假设 是未感染肝细胞被病毒感染的速率, 是被感染肝细胞感染的速率。感染的肝细胞通过自然死亡以 的速率被清除,并通过非细胞溶解过程以a的速率转化为未感染的肝细胞。在血液中游离的病毒在感染的肝细胞中产生的速率和衰变的速率分别为k和 。病毒进入宿主细胞后,抗体以c的速率刺激自身产生 细胞,使病毒以p的速率中和。最后, 是b细胞的自然死亡率。以上所有参数均为正数。易求得系统的非负平衡点为
,,其中:
,,
确定性系统(1)在受到细胞环境、医疗条件以及个人身体素质等随机因素的影响下,则其中的参数 会变得不稳定。考虑到随机激励给系统带来的影响和参数的实际意义以及运算的复杂程度,我们只考虑参数 受白噪声的影响,对其加入随机项: ,,,,则得到一个新的随机非线性微分方程:
(2)
其中 代表白噪声强度, 表示零均值白噪声,即 ,,令 ,,,,代入系统(2)可得
(3)
其中:
,,,,,,
3. 随机HCV模型的初步处理
由随机稳定性的等价定义 [11] 知,系统(3)在平衡点 处的稳定性等价于系统(2)在平衡点 处的稳定性,则系统(3)的特征方程可表示如下:
(4)
其中:
,,
若令 ,其中 为足够小的参数,则通过计算可得特征方程(4)的特征值为: ,,,当 时, ,则特征值为: ,, 是系统(3)的退化临界焦点,那么当 足够小时,系统(3)具有不变流形:
,
则(3)系统可近似代替为。
(5)
其中:
在文献 [12] 中,罗和郭将极坐标变换 和 与伊藤公式相结合,并用随机平均法将系统(3)改写为伊藤随机微分方程:
(6)
和 是独立的标准Wiener过程,并有以下标记:
,
,
,
,
,
因此由以上可得,其振幅为:
(7)
4. 随机稳定性分析
4.1. 局部随机稳定性
讨论线性伊藤随机微分方程的稳定性,就等于方程(7)中 时的稳定性,则有:
(8)
根据解线性伊藤微分方程精确解析解的方法,可得
其中 ,。
根据拟不可积Hamilton系统的原理,线性伊藤随机微分方程Lyapunov指数为 ,则:
由乘积遍历性定理 [11] 知,系统的平凡解以概率1渐进稳定的充份必要条件是:最大Lyapunov指数 ,因此可以得到系统保持局部随机稳定的条件是: 。
因为乘积遍历性定理的最大Lyapunov指数只适用于判断系统平凡解的局部稳定性,对全局稳定性不能判别,所以我们下面讨论一下系统的全局随机稳定性。
4.2. 全局随机稳定性
在随机激励的影响下,漂移系数 和扩散系数 会变得不稳定,经常会出现奇异边界,而得知这种边界上的性态就等价于得知整个扩散过程的性质。所以根据奇异边界理论的边界类别,对系统的平凡解的全局稳定性做出判别。
分为两种情况:
情形1:当 时,系统此时变为如下形式:
(9)
当 时,其为系统的第一类奇异边界;当 时, , 为系统的第二类奇异边界。
根据奇异边界理论,可分别计算出在 边界处的扩散指数、漂移指数和特征标值,即
 ,
, 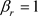 ,
, 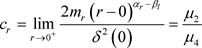 ,
,
若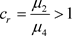 ,则
,则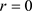 是排斥自然边界;若
是排斥自然边界;若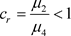 ,则
,则 是吸引自然边界;若
是吸引自然边界;若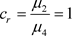 ,则
,则 是严格自然边界。
是严格自然边界。
同理,可分别计算出在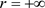 边界处的扩散指数、漂移指数和特征标值,即
边界处的扩散指数、漂移指数和特征标值,即
 ,
, 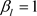 ,
, 
若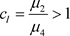 ,则
,则 是吸引自然边界;若
是吸引自然边界;若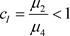 ,则
,则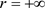 是排斥自然边界;若
是排斥自然边界;若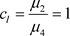 ,则
,则 是严格自然边界。
是严格自然边界。
因此得出系统全局稳定的条件:当 ,
, 是吸引自然边界,
是吸引自然边界,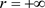 是排斥自然边界,则表
是排斥自然边界,则表
明线性的伊藤随机微分方程的平凡解在概率为1的意义下是稳定的,这也表明系统(2)在含有随机激励时在平衡点处是概率稳定的。
情形2:当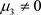 时,系统此时变为如下形式:
时,系统此时变为如下形式:
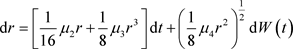 (10)
(10)
当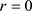 时,其为系统的第一类奇异边界;当
时,其为系统的第一类奇异边界;当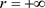 时,
时,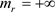 ,
, 为系统的第二类奇异边界。
为系统的第二类奇异边界。
根据奇异边界理论,可分别计算出在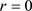 边界处的扩散指数、漂移指数和特征标值,即
边界处的扩散指数、漂移指数和特征标值,即
 ,
, 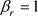 ,
, 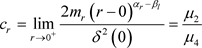
若 ,则
,则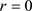 是排斥自然边界;若
是排斥自然边界;若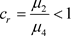 ,则
,则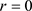 是吸引自然边界;若
是吸引自然边界;若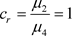 ,则
,则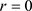 是严格自然边界。
是严格自然边界。
同理,可分别计算出在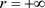 边界处的扩散指数、漂移指数和特征标值,即
边界处的扩散指数、漂移指数和特征标值,即
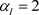 ,
, 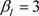 ,
, 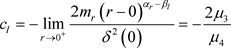 ,
,
若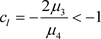 ,即
,即 则
则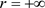 是吸引自然边界;若
是吸引自然边界;若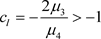 ,即
,即 则
则 是排斥自然边界;若
是排斥自然边界;若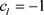 ,即
,即 则
则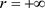 是严格自然边界。
是严格自然边界。
当 是吸引自然边界,
是吸引自然边界,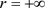 是排斥自然边界,系统所有解曲线都从右边界进入到系统的内部被
是排斥自然边界,系统所有解曲线都从右边界进入到系统的内部被
左边界吸引,当左边界r趋于0处时,所有平凡解是稳定的,因此得出系统全局稳定的条件: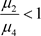 ,
, 。
。
5. 随机Hopf分岔
随机分岔是随机激励系统在系统的某个或某些参数发生微小变化时它的性态也会发生变化的现象,这一部分将应用拟不可积Hamilton系统随机平均法分析系统的随机分岔动力学行为。随机分岔分为两类:动态分岔(D-分岔)与维象分岔(P-分岔)。
5.1. 动态分岔
(1) 当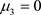 时,系统为:
时,系统为:
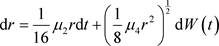 (11)
(11)
当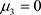 时系统是一个确定性的线性系统,不会发生分岔现象。因此下面讨论
时系统是一个确定性的线性系统,不会发生分岔现象。因此下面讨论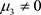 的情形,令
的情形,令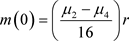 ,
,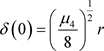 ,由方程生成的连续动态系统为:
,由方程生成的连续动态系统为:
 (12)
(12)
它是方程(11)以x为初值的唯一强解。当 ,
,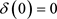 时,0是
时,0是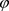 的一个不动点,对此不动点,
的一个不动点,对此不动点,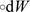 是stratonovich随机微分方程意义下的随机参激,设
是stratonovich随机微分方程意义下的随机参激,设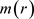 有界,对所有
有界,对所有 满足椭圆性条件
满足椭圆性条件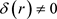 ,保证了最多只有一个平稳概率密度,由振幅
,保证了最多只有一个平稳概率密度,由振幅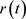 的伊藤微分方程得到(11)式对应的FPK方程:
的伊藤微分方程得到(11)式对应的FPK方程:
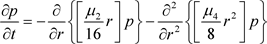 (13)
(13)
令 得到与方程(13)相应的平稳概率密度:
得到与方程(13)相应的平稳概率密度:
 (14)
(14)
其中c为归一化常数,故上述动态系统有不动点和非平凡平稳运动两种平稳状态,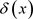 为前者的不变测度
为前者的不变测度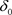 的密度,(14)式为后者的不变测度
的密度,(14)式为后者的不变测度 的密度,为便于研究动态分岔,需分别计算这两个不变测度的Lyapunov指数。
的密度,为便于研究动态分岔,需分别计算这两个不变测度的Lyapunov指数。
考虑线性的伊藤微分方程,得到方程(11)的解:
 (15)
(15)
动态系统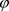 关于不变测度
关于不变测度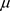 的Lyapunov指数可定义如下:
的Lyapunov指数可定义如下:
 (16)
(16)
将(15)式代入方程(16),这里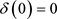 ,
,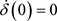 得不动点Lyapunov指数如下:
得不动点Lyapunov指数如下:
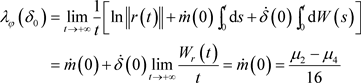 (17)
(17)
以(14)式为密度的不变测度 ,将(15)式代入方程(16),假定有界,并且
,将(15)式代入方程(16),假定有界,并且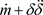 可积,得到Lyapunov指数:
可积,得到Lyapunov指数:
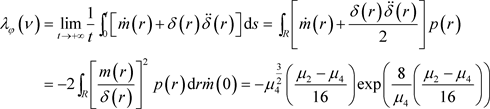 (18)
(18)
令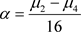 ,于是可得,当
,于是可得,当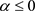 时不动点的不变测度是稳定的,当
时不动点的不变测度是稳定的,当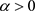 时非平凡状态不变测度
时非平凡状态不变测度
是稳定的,所以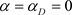 是系统(2)一个D分岔点。
是系统(2)一个D分岔点。
化简系统(14)可得以下方程:
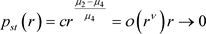 (19)
(19)
其中c为归一化常数,令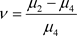 ,显然当
,显然当 时,
时,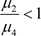 。
。 是一个
是一个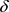 函数,不可积,当
函数,不可积,当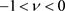 时,
时, 。
。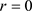 是
是 在该区间上取得最大值的一个点。
在该区间上取得最大值的一个点。 时系统(2)发生D分岔,即
时系统(2)发生D分岔,即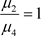 是系统发生D分岔的临界条件。当
是系统发生D分岔的临界条件。当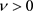 时不存在一个点使得
时不存在一个点使得 取到极大值,则系统(2)不会发生 分岔。
取到极大值,则系统(2)不会发生 分岔。
(2) 当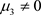 时,令
时,令 ,且
,且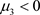 ,
,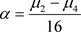 则系统(7)变为:
则系统(7)变为:
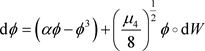 (20)
(20)
当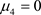 时,经分析可得系统有确定性叉形分岔。
时,经分析可得系统有确定性叉形分岔。 ,
,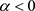 时,只有唯一的不变测度其密度为
时,只有唯一的不变测度其密度为 ;
; ,
,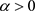 时,有三个不变测度分别为:
时,有三个不变测度分别为: 与两个非平凡平稳状态测度
与两个非平凡平稳状态测度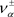 ,其密度为:
,其密度为:
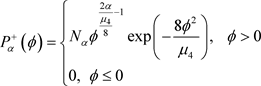 (21)
(21)
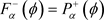 (22)
(22)
式中 ,则有(17)式可得关于
,则有(17)式可得关于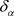 的Lyapunov指数为:
的Lyapunov指数为:
 (23)
(23)
根据遍历性理论,由方程(18),(21)和(23)可计算得出关于两个非平凡平稳状态测度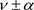 的Lyapunov指数:
的Lyapunov指数:
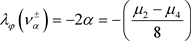 (24)
(24)
由此可知,在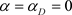 处发生D分岔。
处发生D分岔。
由于(21)式有极值,于是可知在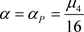 处系统(2)会发生P分岔。
处系统(2)会发生P分岔。
5.2. 维象分岔
这部分考虑线性伊藤微分方程的稳态概率密度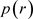 ,从不变测度极值来分析系统的分岔行为。令
,从不变测度极值来分析系统的分岔行为。令
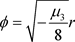 ,
,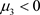 则系统(7)变为:
则系统(7)变为:
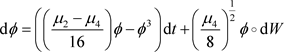 (25)
(25)
则根据伊藤方程的振幅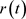 得到方程(25)的FPK方程如下:
得到方程(25)的FPK方程如下:
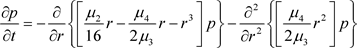 (26)
(26)
由初值条件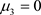 ,
, ,其中
,其中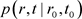 是扩散过程的转移概率密度,
是扩散过程的转移概率密度,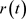 的不变测度是稳态概率密度,得到其退化系统的解如下:
的不变测度是稳态概率密度,得到其退化系统的解如下:
 (27)
(27)
通过计算可得:
 (28)
(28)
由Namachivays [11] 理论知,非线性随机动力系统稳态性主要是通过不变测度的极值显示的,能显示出系统最根本的稳态性行为。当噪声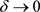 时,
时, 的极值几乎可以表示确定系统的稳态行为。若
的极值几乎可以表示确定系统的稳态行为。若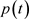 在
在 处可取得极大值,则轨线会在
处可取得极大值,则轨线会在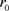 处的邻域内停留较长时间,即
处的邻域内停留较长时间,即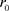 在概率意义下是稳定的点。
在概率意义下是稳定的点。
6. 数值模拟
由以上得知,原系统的响应过程为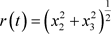 ,所以响应过程的联合概率密度函数为
,所以响应过程的联合概率密度函数为 。选取参数
。选取参数 ,根据实际情况给参数
,根据实际情况给参数 赋予一定的值,使得
赋予一定的值,使得 ,然后选取
,然后选取 为分岔参数。设
为分岔参数。设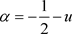 ,下图(图1~3)就是模拟的平稳概率密度函数图和联
,下图(图1~3)就是模拟的平稳概率密度函数图和联
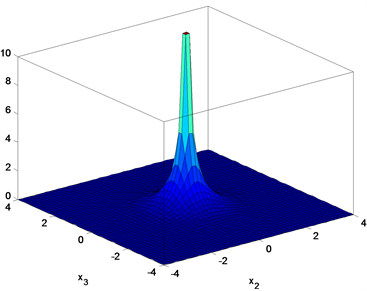
合概率密度函数图。当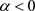 时,图1中的平稳概率密度函数图像是一个单调递减的函数,联合概率密度函数图像是单峰尖状的;当
时,图1中的平稳概率密度函数图像是一个单调递减的函数,联合概率密度函数图像是单峰尖状的;当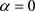 时,图2中平稳概率密度函数图像从单峰值函数变为单调递减函数,从
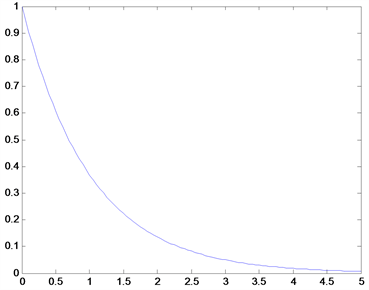
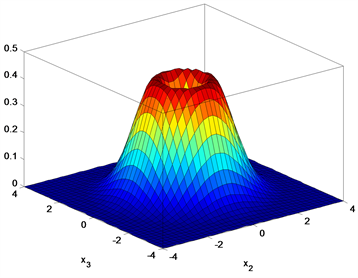
时,图2中平稳概率密度函数图像从单峰值函数变为单调递减函数,从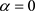 时的联合概率密度函数图可以看出系统未发生分岔;当
时的联合概率密度函数图可以看出系统未发生分岔;当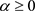 时,在图3中可以看到,在
时,在图3中可以看到,在 时发生分岔,联合概率密度函数图像从单峰形状变为火山口形状。
时发生分岔,联合概率密度函数图像从单峰形状变为火山口形状。
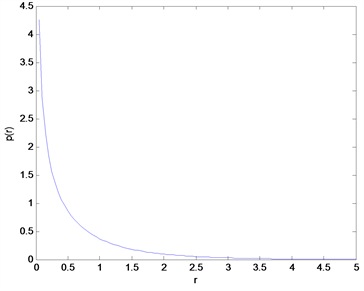
(a) 的平稳概率密度图 (b)
的平稳概率密度图 (b)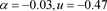 的联合概率密度图
的联合概率密度图
Figure 1. The stationary probability density graph and the corresponding joint probability density graph when 
图1. 当 时的平稳概率密度图和相对应的联合概率密度图
时的平稳概率密度图和相对应的联合概率密度图

(a) 的平稳概率密度图 (b)
的平稳概率密度图 (b) 的联合概率密度图
的联合概率密度图
Figure 2. The stationary probability density graph and the corresponding joint probability density graph when 
图2. 当 时的平稳概率密度图和相对应的联合概率密度图
时的平稳概率密度图和相对应的联合概率密度图

(a)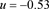 的平稳概率密度图 (b)
的平稳概率密度图 (b) 的联合概率密度图
的联合概率密度图
Figure 3. The stationary probability density graph and the corresponding joint probability density graph when 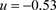
图3. 当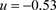 时的平稳概率密度图和相对应的联合概率密度图
时的平稳概率密度图和相对应的联合概率密度图
7. 结论
本文主要运用随机激励的Hamilton理论和随机平均法分析了HCV模型的动力学行为。结果表明,HCV系统在受到白噪声影响时会变得不稳定,并且发生随机分岔行为,根据参数的实际意义选取 作为分岔参数,当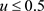 时,图3中的图3(a)图从单调函数变为单峰函数,图3(b)图像由单峰状变化为火山口状,系统发生了分岔。说明此刻可能不利于病毒的控制,需采取一定的策略,以减缓病毒的感染速率,防止病情的恶化。
时,图3中的图3(a)图从单调函数变为单峰函数,图3(b)图像由单峰状变化为火山口状,系统发生了分岔。说明此刻可能不利于病毒的控制,需采取一定的策略,以减缓病毒的感染速率,防止病情的恶化。
基金项目
国家自然科学基金(批准号:61863022)。
文章引用
秦 旺,叶正伟,梁相玲,邓生文. 一类HCV模型的随机稳定性和分岔分析
Stochastic Dynamics Analysis of HCV Virus Model[J]. 应用数学进展, 2020, 09(04): 509-519. https://doi.org/10.12677/AAM.2020.94062
参考文献
- 1. Wodarz, D. (2003) Hepatitis C Virus Dynamics and Pathology: The Role of CTL and Antibody Responses. Journal of General Virology, 84, 1743-1750. https://doi.org/10.1099/vir.0.19118-0
- 2. Wodarz, D. (2005) Mathematical Models of Immune Effect or Responses to Viral Infections: Virus Control versus the Development of Pathology. Journal of Computational and Applied Mathematics, 184, 301-319. https://doi.org/10.1016/j.cam.2004.08.016
- 3. Li, J., Men, K., Yang, Y., et al. (2015) Dynamical Analysis on a Chronic Hepatitis C Virus Infection Model with Immune Response. Journal of Theoretical Biology, 365, 337-346. https://doi.org/10.1016/j.jtbi.2014.10.039
- 4. Wang, W. and Ma, W. (2018) Hepatitis C Virus Infection Is Blocked by HMGB1: A New Nonlocal and Time-Delayed Reaction-Diffusion Model. Applied Mathematics and Com-putation, 320, 633-653. https://doi.org/10.1016/j.amc.2017.09.046
- 5. Neumann, A.U., Phillips, S., Levine, I., et al. (2010) Novel Mechanism of Antibodies to Hepatitis B Virus in Blocking Viral Particle Release from Cells. Hepatology, 52, 875-885. https://doi.org/10.1002/hep.23778
- 6. Chen, S.S., Cheng, C.Y. and Takeuchi, Y. (2016) Stability Analysis in Delayed within-Host Viral Dynamics with Both Viral and Cellular Infections. Journal of Mathematical Analysis and Application, 488, Article ID: 124047. https://doi.org/10.1016/j.jmaa.2016.05.003
- 7. Pan, S. and Chakrabarty, S.P. (2018) Threshold Dynamics of HCV Model with Cell-to-Cell Transmission and a Non-Cytolytic Cure in the Presence of Humoral Immunity. Commu-nications in Nonlinear Science and Numerical Simulation, 61, 180-197. https://doi.org/10.1016/j.cnsns.2018.02.010
- 8. Li, D., Cui, J., Liu, M. and Liu, S. (2015) The Evolutionary Dy-namics of Stochastic Epidemic Model with Nonlinear Incidence Rate. Bulletin of Mathematical Biology, 77, 1705-1743. https://doi.org/10.1007/s11538-015-0101-9
- 9. Riley, S. (2007) Large-Scale Spatial-Transmission Models of Infectious Disease. Science, 316, 1298-1301. https://doi.org/10.1126/science.1134695
- 10. 白宝利. 一类随机的SIR流行病模型的动力学行为分析[D]: [硕士学位论文]. 兰州: 兰州交通大学, 2017.
- 11. 朱位秋. 非线性随机动力学与控制Hamilton理论体系框架[M]. 北京: 科学出版社, 2003.
- 12. Luo, C. and Guo, S. (2017) Stability and Bifurcation of Two-Dimensional Stochastic Differential Equations with Multiplicative Excitations. Bulletin of the Malaysian Mathematical Sciences Society, 40, 795-817. https://doi.org/10.1007/s40840-016-0313-7
NOTES
*第一作者。