Advances in Applied Mathematics
Vol.
09
No.
11
(
2020
), Article ID:
38639
,
9
pages
10.12677/AAM.2020.911221
求解极大极小问题的共轭梯度法
郝月
青岛大学数学与统计学院,山东 青岛

收稿日期:2020年10月25日;录用日期:2020年11月11日;发布日期:2020年11月18日

摘要
本文研究了极大极小问题的求解方法,利用指数罚函数对该问题进行光滑化处理,将其转化成光滑的无约束优化问题,并利用共轭梯度法来求解含有罚参数的无约束优化问题。最后,我们给出了数值算例来验证该算法求解极大极小问题的有效性。
关键词
极大极小,指数罚函数,光滑化,共轭梯度法
Conjugate Gradient Method for Solving Minimax Problems
Yue Hao
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong

Received: Oct. 25th, 2020; accepted: Nov. 11th, 2020; published: Nov. 18th, 2020

ABSTRACT
This paper studies the method for solving the minimax problem, the exponential penalty function is used for smoothing the problem which can be transformed into a smooth unconstrained optimization problem. We also use the conjugate gradient method to solve the unconstrained optimization with penalty parameters problem. Finally, numerical results are given to illustrate the effectiveness of the algorithm for solving minimax problems.
Keywords:Minimax, Exponential Penalty Function, Smoothing Method, Conjugate Gradient Method

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
极大极小问题是一类重要的非光滑优化问题,且在工程设计、经济管理 [1] [2] 等领域有着广泛的应用,同时也与非线性规划问题有着密切的联系。
极大极小问题的一般形式为
(1)
其中, 是连续可微的函数。
近年来,众多学者对极大极小问题的算法进行了研究。通过构造罚函数,提出一个有效的算法求解极大极小问题,如文献 [3];通过构造可调节熵函数的区间扩展和一些区域删除测试规则, [4] 提出了一种新的区间算法,该算法可以获得极大极小问题的最优解;文献 [5] 提出了一种截断的集合平滑牛顿法来解决极小极大问题。最近,一种用于求解极大极小问题的平滑FR共轭梯度法由文献 [6] 提出,其实验结果表现良好。
综上文献,我们知道罚函数在极大极小问题的求解过程中起到了重要的作用,该罚函数由 [7] 提出,其形式为
(2)
其中,t是罚参数, 是光滑可微的函数。利用罚函数(2),极大极小问题(1)可以被转化为一个光滑的无约束优化问题,其形式为
(3)
是光滑可微函数,且被定义为
其中 是罚参数。此时,对非光滑的极大极小问题(1)的求解可以等价于对光滑的无约束优化问题(3)的求解。
另外,我们还对带有张量结构的极大极小问题进行研究。一个m阶n维的张量 ,其中 ,对一个n维向量x, 是一个向量,它的第i的元素是
下面我们给出具有张量结构的极大极小问题的形式。首先定义如下函数:
(4)
其中, 是一个m阶n维的张量, 是n维向量。对(4)中的绝对值项进行光滑化处理后,有
则对于 ,由(2)可得出如下函数
此时,对于下式
利用指数罚函数(2),我们可以得到如下光滑的函数
(5)
那么,对于张量结构的极大极小问题就可以转化为对(5)式的求解。
本文的目的是使用共轭梯度法来求解光滑后的极大极小问题,具体安排如下:第2部分,给出求解光滑后的极大极小问题的算法;第3部分给出该算法求解两类极大极小问题的数值实验;第4部分总结。
2. 共轭梯度算法
共轭梯度类算法 [8] [9] [10] 由于其收敛速度快、存储量小以及稳定性高等优点被广泛应用于无约束优化问题的求解中,其最早由Hestenes和Stiefle提出。著名的共轭梯度法有Fletcher-reeves (FR)方法,Hestenes-Stiefel (HS)方法和Dai-Yuan (DY)方法等。本节给出针对光滑后的极大极小问题的共轭梯度法及其算法。
设 为当前迭代点,对光滑后的极大极小问题(3),即一个无约束优化问题
记函数值 ,梯度 ,则搜索方向为
其中, 为一个参数,常用的 有:
其中, 。此时,共轭梯度法的迭代形式为
其中 为线搜索产生的步长。常用的线搜索为Wolfe线搜索:
以及Amijo线搜索
为解决更复杂的无约束优化问题以及得到更精确的解,谱共轭梯度法 [11] [12] [13]、三项共轭梯度法 [14] [15] [16] 等方法被提出,在解决大规模无约束优化问题、互补问题以及张量等问题都有良好的数值效果。结合文献 [11],本文给出针对光滑化后的极大极小问题的搜索方向与步长:
(6)
在(6)中,
步长 满足
(7)
(8)
其中, 。
下面,我们给出求解极大极小问题的光滑化共轭梯度法:
算法2.1
步1:给定常数 ,初始点 ,令 ;
步2:若 ,则停止计算,否则转步3;
步3:根据(7)、(8)计算步长 ;
步4:令 ,,由(6)计算搜索方向 ;
步5:计算 ,,令 ,转步2。
为证明算法的收敛性,我们首先给出如下假设:
假设2.1:
(A1) 水平集 有界,水平集为 ;
(A2) 在 的一个邻域U中,函数是连续可微且其导数是Lipschitz连续的,即
其中L是Lipschitz常数。
由假设2.1可得,存在一个常数 ,使得
引理2.1: 由(6)式给出,则
(9)
证 当 时,(9)式显然成立,假设 时满足 ,则
引理2.2:若假设2.1成立,则
(10)
证 由假设A(2)和(8)式,我们有
移项后两边同时平方可得
结合(7)式,
故由引理2.1可得(10)式成立。
由引理2.1和引理2.2,我们可以得出如下的收敛性定理。
定理2.1:若假设2.1成立,则算法2.1满足
(11)
证 反证法,假设定理不成立,存在常数 ,对任意 ,有
根据(6)式,有
两边同时平方后除以 ,有
即
因此,我们有
与假设矛盾,因此(11)式成立。
3. 数值实验
本部分,我们给出用算法2.1求解极大极小问题的数值算例,3.1中计算常规的极大极小问题,算例取自文献 [3],通过给出算例结果与最优值的误差证明算法的有效性。3.2中给出算法2.1计算带有张量结构的极大极小问题的数值结果,数值结果表明算法2.1在求解带有张量结构的极大极小问题时有良好的数值表现。
3.1. 极大极小问题
本部分给出光滑化算法计算极大极小问题的数值算例,其中的参数设置具体为 ,,,,。表1给出实验结果,其中n,m分别为变量、函数的数目,图1~3为算法2.1在求解算例时,函数值随着迭代步数的数值表现。由表1和图1~3我们可以观察到算法2.1在求解极大极小问题时具有良好的数值表现。
例1 Cresent [3]
例2 Mifflin 1 [3]
例3 Mifflin 2 [3]
Table 1. Numerical results for example 1 - 3
表1. 例1~例3的实验结果

Figure 1. The numerical results of Cresent
图1. Cresent的实验结果

Figure 2. The numerical results of Mifflin 1
图2. Mifflin 1的实验结果
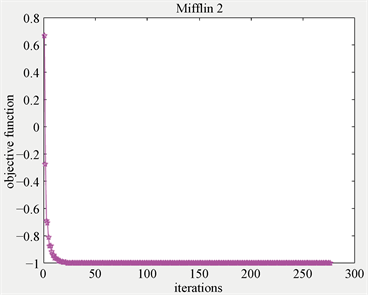
Figure 3. The numerical results of Mifflin 2
图3. Mifflin 2的实验结果
3.2. 带张量结构的极大极小问题
本部分给出算法2.1求解带有张量结构的极大极小问题的数值算例,为了便于计算,数值算例中的张量使用的是对称张量,其中的参数设置为 ,,,,,且选取 作为算法的终止条件。表2给出实验结果,其中n,m分别是张量的阶数和维数,图4~5为算法2.1在求解算例时,函数值随着迭代步数的数值表现。由表2和图4~5我们可以观察到算法2.1可以有效求解带有张量结构的极大极小问题。
考虑两个3阶2维的张量 和 ,以及两个向量为 和 ,给出如下两个算例:
例4: 为 ,其余元素为3, 为 ,其余元素为3。初始向量为 。
例5: 为 ,其余元素为3, 为 ,其余元素为6。初始向量为 。
Table 2. Numerical results for example 4 - 5
表2. 例4~例5的实验结果
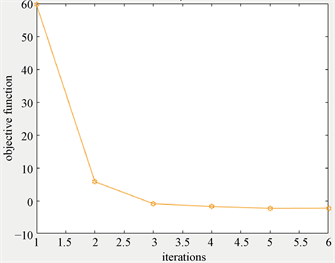
Figure 4. The numerical results of example 4
图4. 例4的实验结果

Figure 5. The numerical results of example 5
图5. 例5的实验结果
4. 结论
本文通过指数罚函数,对极大极小问题进行光滑化处理,将非光滑的极大极小问题转化为光滑的无约束优化问题,并给出针对带有罚参数的无约束优化问题的共轭梯度算法。为验证算法的有效性,我们同时给出了该算法求解常规的极大极小问题和带有张量结构的极大极小问题的数值实验,根据数值实验的结果,该算法在迭代次数、下降速度、误差等方面都具有良好的表现。在以后的研究中,对于更复杂的大规模的极大极小问题,可以运用不同的线搜索或不同的步长进行优化,以得到更快的下降速度和更良好的数值表现。
文章引用
郝 月. 求解极大极小问题的共轭梯度法
Conjugate Gradient Method for Solving Minimax Problems[J]. 应用数学进展, 2020, 09(11): 1916-1924. https://doi.org/10.12677/AAM.2020.911221
参考文献
- 1. Polak, E., Higgins, J.E. and Maynes, D.Q. (1992) A Barrier Function Method for Minimax Problems. Mathematical Programming, 54, 155-176. https://doi.org/10.1007/BF01586049
- 2. Polak, E. (1987) On the Mathematical Foundations of Non Differentiable Optimization in Engineering Design. SIAM Review, 29, 21-91. https://doi.org/10.1137/1029002
- 3. Pillo, G., Grippo, L. and Lucidi, S. (1993) A Smooth Method for the Finite Minimax Problem. Mathematical Programming, 60, 187-214. https://doi.org/10.1007/BF01580609
- 4. Li, S.B., Cao, D.X., Wang, H.J. and Deng, K.Z. (2004) Interval Adjustable Entropy Algorithm for a Class of Unconstrained Discrete Minimax Problems. Applied Mathematics, 19, 37-43. https://doi.org/10.1007/s11766-004-0019-8
- 5. Xiao, Y. and Bo, Y. (2010) A Truncated Aggregate Smoothing Newton Method for Minimax Problems. Applied Mathematics and Computation, 216, 1868-1879. https://doi.org/10.1016/j.amc.2009.11.034
- 6. Pang, D.Y., Du, S.Q. and Ju, J.J. (2016) The Smoothing Fletcher-Reeves Conjugate Gradient Method for Solving Finite Minimax Problems. Science Asia, 42, 40-45. https://doi.org/10.2306/scienceasia1513-1874.2016.42.040
- 7. Li, X.S. (1991) An Aggregate Function Method for Nonlinear Programming. Science in China, Series A, 12, 1467-1473.
- 8. Fletcher, R. and Reeves, C.M. (1964) Function Minimization by Conjugate Gradients. Computer Journal, 7, 149-154. https://doi.org/10.1093/comjnl/7.2.149
- 9. 张丽, 周伟军. Armijo线性搜索下Hager-Zhang共轭梯度法的全局收敛性[J]. 数学物理学, 2018, 28A(5): 840-845.
- 10. 戴彧虹, 袁亚湘. 非线性共轭梯度法[M]. 上海: 上海科学技术出版社, 2000.
- 11. Du, S.Q. and Chen, Y.Y. (2008) Global Convergence of a Modified Spectral FR Conjugate Gradient Method. Applied Mathematics and Computation, 202, 766-770. https://doi.org/10.1016/j.amc.2008.03.020
- 12. Birgin, E.G. and Martinez, J.M. (2001) A Spectral Conjugate Gradient Method for Unconstrained Optimization. Applied Mathematics and Computation, 43, 117-128. https://doi.org/10.1007/s00245-001-0003-0
- 13. 李向利, 师娟娟, 董晓亮. 一类修正的非单调谱共轭梯度法及其在非负矩阵分解中的应用[J]. 数学物理学报, 2018, 38(5): 954-962.
- 14. Andrei, N. (2013) A Simple Three-Term Conjugate Gradient Algorithm for Unconstrained Optimization. Journal of Computational and Applied Mathematics, 241, 19-29. https://doi.org/10.1016/j.cam.2012.10.002
- 15. Dong, X.L., Liu, H.W. and He, Y.B. (2015) New Version of the Three-Term Conjugate Gradient Method Based on Spectral Scaling Conjugacy Condition That Generates Descent Search Direction. Applied Mathematics and Computation, 269, 606-617. https://doi.org/10.1016/j.amc.2015.07.067
- 16. Koorapetse, M.S. and Kaelo, P. (2018) Globally Convergent Three-Term Conjugate Gradient Projection Methods for Solving Nonlinear Monotone Equations. Arabian Journal of Mathematics, 7, 289-301. https://doi.org/10.1007/s40065-018-0206-8
